例析數列問題中的“安全隱患”

?邢臺市第十九中學 崔勝峰

數列是高中數學的重要內容，是培養學生數學素養的重要載體，同時也是高考、競賽及其他各類考試命題的熱點.學生在學習這部分知識時，經常會因忽視“安全隱患”而導致解題的失誤.本文中列舉這些“安全隱患”，以期起到防微杜漸的作用.

1安全隱患一：基本概念不清

例1已知數列{an}是遞增數列，且對于任意的n∈N*，an=n2-λn恒成立，求實數λ的取值范圍.

錯解1:因為數列{an}是遞增數列，所以an+1>an恒成立，即λ<2n+1恒成立.

所以，λ的范圍為(-∞，2n+1).

正確1：因為數列{an}是遞增數列，所以an+1>an恒成立，即λ<2n+1恒成立.

于是有<(2n+1)min.

因為n∈N*時，2n+1的最小值是3，所以λ的取值范圍為(-∞，3).

點評：求參數λ的范圍(或值)，應該是一個具體的范圍(或數)，而不應是一個含變量的代數式.

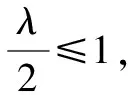
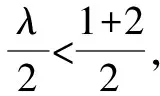
所以，λ的取值范圍為(-∞，3).

點評：用函數的觀點研究數列的性質時，一定要注意其定義域是N*或其子集這一特性，因而數列的圖象是一群孤立的點.

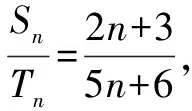
錯解:設Sn=(2n+3)k，Tn=(5n+6)k,k≠0.

于是a7=S7-S6=2k，b7=T7-T6=5k.

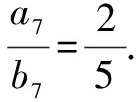
正確1：設Sn=kn(2n+3),Tn=kn·(5n+6),k≠0.

于是a7=S7-S6=29k，b7=T7-T6=71k.

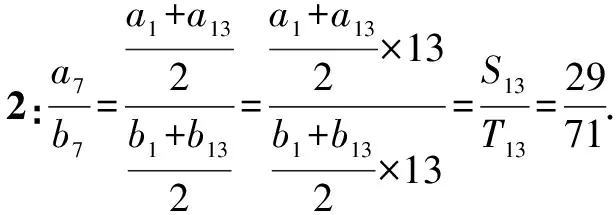
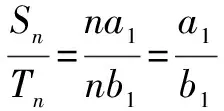
2 安全隱患二：忽視公式條件

例3已知數列{an}的前n項和Sn=3n+1，求數列{an}的通項公式.

錯解:因為Sn=3n+1，所以Sn-1=3n-1+1.

故an=Sn-Sn-1=2×3n-1.

正確：當n=1時，a1=S1=4.

當n≥2時，an=Sn-Sn-1=2×3n-1.

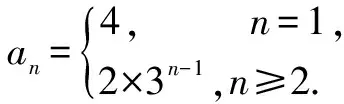
點評：由Sn求an時，一定要分n=1和n≥2進行討論，因為a0,S0是沒有意義的.解出兩段后進行驗證，若不能統一則要寫成分段函數的形式.

例4已知等比數列{an}中，a3=2,S3=6，求通項公式an.

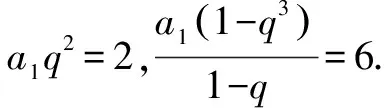
于是2q3-3q2+1=0，即(q-1)2(2q+1)=0.

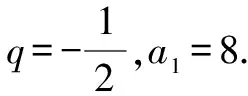
所以an=(-1)n-124-n.

正解：當q=1時，a1=a2=a3=2,S3=6，符合題意.所以q=1時，an=2.

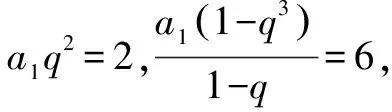
綜上所述，數列{an}的通項公式為an=2或an=(-1)n-124-n.

點評：利用等比數列前n項和公式時，要特別注意對公比q=1和q≠1 進行判斷[1]，以免漏掉公比q=1的情形.

3 安全隱患三：忽視隱含條件

例5首項為18的等差數列{an}，從第10項起開始為負數，求公差d的取值范圍.

錯解:因為a10=a1+9d=18+9d，所以18+9d<0，解得d<-2.

正解：由an=18+(n-1)d，a9≥0,a10<0，得18+8d≥0,18+9d<0.

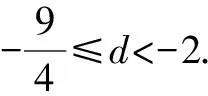
點評：上述錯解忽略了“開始”一詞的含義，即第10項是等差數列的第一個負項，前9項都是非負的，所以審題務必仔細.

例6已知數列-1,a1,a2,-9成等差數列，-1,b1,b2,b3,-9成等比數列，求(a2-a1)b2的值.

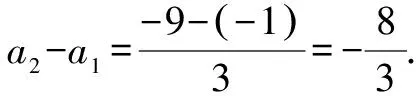
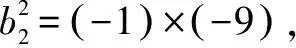
當b2=3時，(a2-a1)b2=-8；當b2=-3時，(a2-a1)b2=8.

綜上所述，可得(a2-a1)b2=±8.

正解：因為-1,a1,a2,-9成等差數列，所以

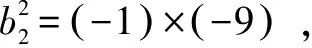
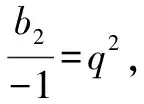
故(a2-a1)b2=8.

點評：b2=(-1)q2<0是題目中隱含的條件，利用等比數列的性質解題時要特別注意這類條件.

4 安全隱患四：忽視內在規律

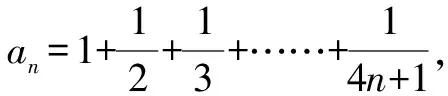
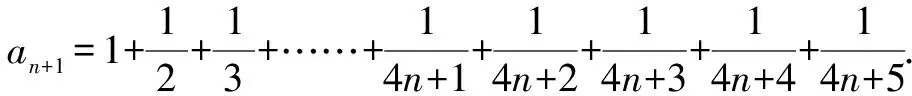
點評：上述錯解誤以為只添加一項，其內在規律是分子均為1，分母是連續的正整數，所以應增加4項.

例8求1+3+32+33+……+3n的和.

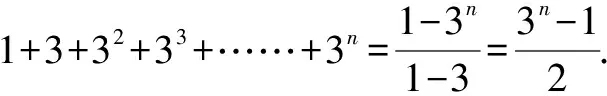
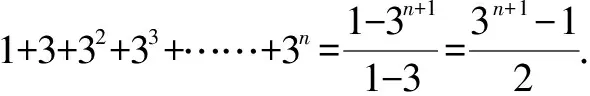
點評：數列求和時，一定要弄清楚項數，本題是n+1項而不是n項，所以要認真審題，觀察出內在規律.

5 學習建議

基于以上常出現的這些失誤，提出一些建議，期望在學習數列的過程中對學生有所幫助.

(1)掌握基本知識.系統掌握數列的有關概念、表示，特別是等差數列和等比數列的定義、性質和公式.

(2)掌握基本方法.數列是一類特殊的函數，因而可以用函數的思想解決求通項公式an和前n項和Sn的問題；運用方程的思想[2]，設出基本量首項、公差、公比等，列方程求解，特別注意要會用“設而不求，整體代入”來簡化運算；運用分類討論思想，如對項數n是奇數還是偶數的討論，公比q是否等于1的討論，等等；運用等價轉化思想，如an與Sn的轉化，非特殊數列通過加減項轉化為特殊數列，等等；另外，如觀察法，類比法，公式法，待定系數法，換元法，錯位相減法，分組求和法，裂項相消法，倒序相加法的使用等.

(3)加強綜合應用.把數列知識與函數、方程、不等式、平面向量、二項式定理、解析幾何、概率、實際問題等相結合，提高綜合運用知識解決問題的能力.