運用分類討論思想解題“五緊扣”法
?福建省廈門市第六中學 王 楠
1 引言
分類討論的數學思想和方法,在高中數學解題中運用十分廣泛.由于這種方法在解答題型較復雜、難度較大、綜合性較強的數學問題中具有極大的靈活性、便捷性與實用性[1],深受命題人的青睞,成為歷年來高考的高頻考點,因此我們要高度重視和加強分類討論思想的學習與訓練,特別是要熟練地掌握“五緊扣”法的答題方法與技巧.
2 運用分類討論思想解題“五緊扣”法
2.1 緊扣概念的定義

例1解不等式:3|x+2|+3|x-1|≥28.
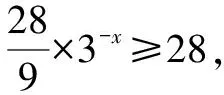
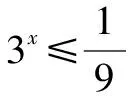
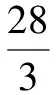
綜上所述,原不等式的解集為{x|x≤-2,或x≥1}.
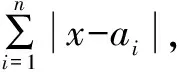
例2設復數z=cosα+(1-sinα)i,α∈[0,2π),求復數z的輻角主值argz.
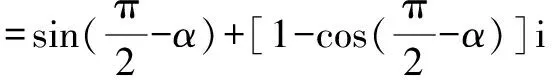
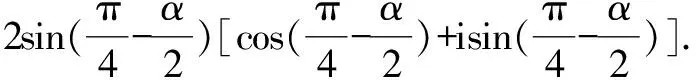
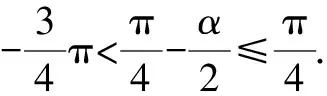
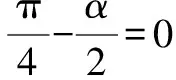
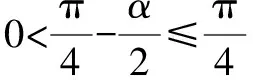
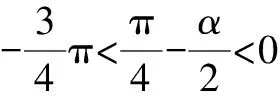
思路與方法:解本題的關鍵是緊扣輻角主值的概念進行分類討論,z=r(cosθ+isinθ)(r>0)中在[0,2π)內的θ稱為復數z的輻角主值.
2.2 緊扣運算的要求
很多數學運算都有一定的要求.例如,分解因式、解方程、解不等式等問題,要弄清楚是在實數范圍內還是復數范圍內解答;在實數范圍內,被開方數開偶數次方時不可以為負數,代數式的運算順序與法則都有明確的要求;等等.
例3解方程:x2-2xysinθ+y2=0(θ為常量).
解:原方程可變形為(x-ysinθ)2+(ycosθ)2=0.
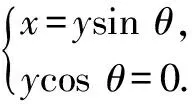
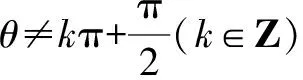
當cosθ=0時,又分為下列兩種情況:
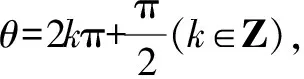
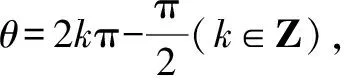
思路與方法:本題是緊扣運算要求進行二級分類,需要注意的是,解答時不能只簡單地按cosθ(除數)是否為零進行一級分類,這樣很容易出錯,尤其是在解三角形類問題中更要注意.
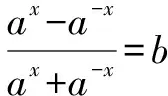
解:原方程變形為ax-a-x=b·ax+b·a-x,即
(1-b)a2x=1+b.
①
當b=1時,①式無解,原方程無解;

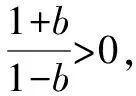
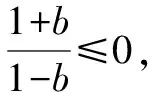
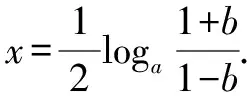
思路與方法:當題目出現多個參數時,為了避免盲目性,應該先考慮變形,在明確“方向”后再考慮分類討論.例4中就出現了a,b兩個參數,應先將原方程變形,然后把a看作已知數,再對參數b進行分類討論.
2.3 緊扣公式定理的限制條件
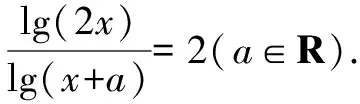
解:原方程與下面混合組
同解,其中⑤式即x2+2(a-1)x+a2=0的判別式為
Δ=4(a-1)2-4a2=4(1-2a).
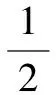
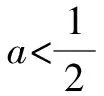
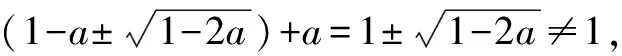
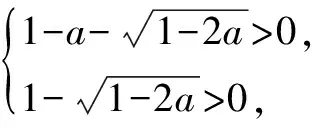
思路與方法:在分類討論時要遵循“不重復,不遺漏”的原則,本題最后的綜述就未忘記a≤0的情況,這樣就可以防止出現遺漏現象.
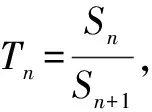
解:當q=1時,由Sn=n,Sn+1=n+1,可得
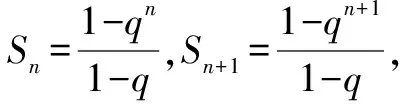
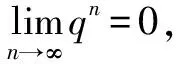
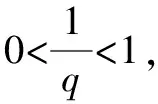
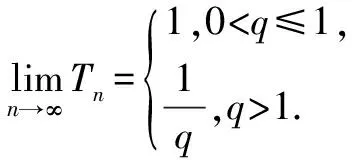
思路與方法:本題將分類討論的結果用分段形式簡潔地表示出來,給人以清晰的感覺,同時分類討論也做到了不重不漏,一清二楚.
2.4 緊扣函數的性質
對某些涉及到函數的單調性、值域范圍等數學問題,要緊扣函數的性質以及分類討論參數的不同取值情況.
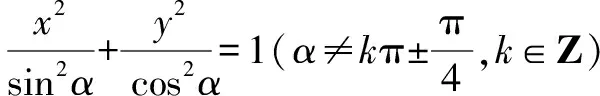
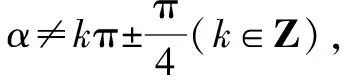
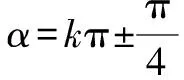
例8已知a>0,a≠1,解關于x的不等式
loga(x2-2ax-2a2)>2.
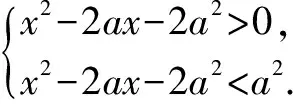
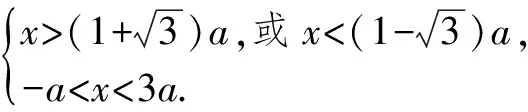
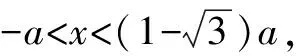
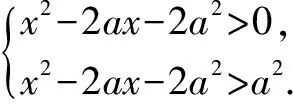

所以x<-a,或x>3a.
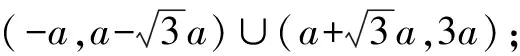
思路與方法:解對數不等式必須考慮相應對數函數的單調性,因此需對含有參數的底數進行分類討論,這既是解題的要求,也是要掌握的方法與技巧.
2.5 緊扣圖形的位置變化情況
在幾何題型中,經常會碰到圖形可能涉及多種位置的不同情況,因此需要分類討論.
例9a,b,c,d是空間四條直線,如果a⊥c,b⊥c,a⊥d,b⊥d,那么( ).
A.a∥b或c∥d
B.a∥b且c∥d
C.a,b,c,d中至多有一對直線互相平行
D.a,b,c,d任何兩條直線都不平行
解:若a,b相交,必能確定一個平面α,由題設可知c⊥α,d⊥α,則c∥d;
若a∥b,滿足題設的直線c,d位置關系不定,可能平行、可能相交、也可能異面;
若a,b異面,由c⊥a,c⊥b,則c平行或重合于a,b的公垂線,同理,d也平行或重合于a,b的公垂線,得c∥d.
綜上所述,四線之中必有一對相互平行.故選:A.
思路與方法:本題中涉及四條直線,元素較多,關系復雜,我們只能先按其中某兩條直線的位置關系進行分類討論.
例10若復數z,z2,z3在復平面上所對應的三點A,B,C組成直角三角形,且|z|=2,求z.

解得z=±ki,于是|z|=|k|=2.故z=±2i.
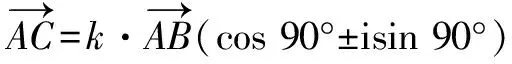
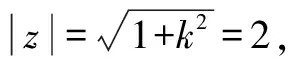
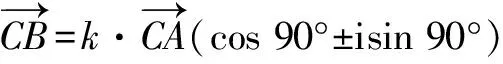
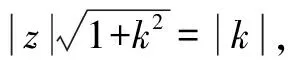
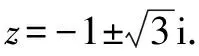
思路與方法:根據題設條件,A,B,C三點都有可能作為直角頂點,所以要分三種情況進行討論.
3 總結
從上述典型例題的解答中可以看出,分類討論是一種很重要的思想方法.運用這種方法的關鍵是要處理好“分化”與“組合”、“局部”與“整體”之間的辯證統一關系[2],在此基礎上還要多練習,勤思考,善于總結,長此堅持下去,一定能夠不斷提高數學解題能力.

