2022年北京高考導數壓軸題解答

?北京市懷柔區第一中學 于海龍

1 試題呈現

(2022年北京高考數學第20題)已知函數f(x)=exln (1+x).

(Ⅰ)求曲線y=f(x)在點(0,f(0))處的切線方程；

(Ⅱ)設g(x)=f′(x)，討論函數g(x)在[0,+∞)上的單調性；

(Ⅲ)證明：對任意的s,t∈(0,+∞)，有f(s+t)>f(s)+f(t).

2 解法分析及詳解

2.1 第(Ⅰ)問的解答

本小題求曲線y=f(x)在點(0,f(0))處的切線方程，先求f′(x)，得f′(0)即為曲線在點(0,f(0))處的切線的斜率，進而求出切線方程.

又因為f(0)=0，f′(0)=1，所以曲線y=f(x)在點(0,f(0))處的切線方程為y=x.

2.2 第(Ⅱ)問的解答

本小題討論函數g(x)在[0,+∞)上的單調性，依題意有如下兩種解法，如圖1所示.

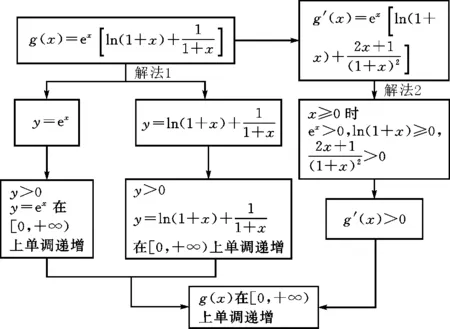
圖1

思路一：根據導數與函數單調性的關系，通過導函數的正負研究函數的單調性.若導函數無變號零點，則可判斷導函數恒正或恒負的情況.

解法1:通法——從導數入手.

所以函數g(x)在[0,+∞)上單調遞增.

思路二：研究復雜函數的單調性，可以將復雜的函數分解，研究局部性質，通過整合，依托單調性定義，借助不等式的性質解決問題.

解法2:分解函數，依托不等式性質與單調性定義.

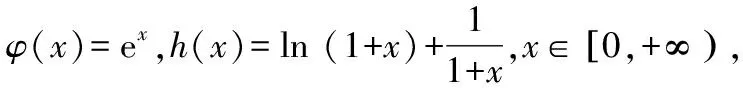
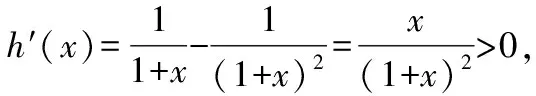
又因為φ(x)在[0,+∞)上單調遞增，且φ(x)>0，所以?x1,x2∈[0,+∞)且x1

φ(x2)>φ(x1)>0，h(x2)>h(x1)>0，

所以φ(x2)h(x2)>φ(x1)h(x2)，即g(x2)>g(x1).

故函數g(x)在[0,+∞)上單調遞增.

2.3 第(Ⅲ)問的解答

本小題的本質是研究函數的最值問題.依題意有如下三類(五種)證明方法，如圖2所示.

圖2

思路一(代數維度)：本題所證不等式中有兩個變量，兩側均有相同的變量，故需要選擇其中一個為主元進行研究，從而構造函數，通過最值證明不等式.

證法1：常規方法——選擇主元，直接移項構造新函數.

令m(x)=f(x+t)-f(x)-f(t)=ex+t·ln (1+x+t)-exln (1+x)-etln (1+t)(x>0)，則

因為t>0，則et>1，且ex≥1+x恒成立，所以

因此m(x)在[0,+∞)上單調遞增.

再由s>0，得m(s)>m(0)，即f(s+t)-f(s)-f(t)>f(0+t)-f(0)-f(t)=-f(0).

由f(0)=0，得f(s+t)-f(s)-f(t)>0.

所以f(s+t)>f(s)+f(t)成立.

事實上，證法1可以優化：

令m(x)=f(x+t)-f(x)-f(t)(x>0)，則

m′(x)=f′(x+t)-f′(x)=g(x+t)-g(x).

由(Ⅱ)中g(x)在[0,+∞)上單調遞增，則由t>0得s+t>s，從而g(x+t)>g(x)即m′(x)>0.……