基于特征嵌入的學生知識點熟練度預測①

史浩杰,李 幸,賈俊鋮,匡 健,章 紅

1(蘇州大學 計算機科學與技術學院,蘇州 215006)

2(初速度(蘇州)科技有限公司,蘇州 215100)

在學生學習過程中,大多數學生都是需要練題來提升自己的能力.在如今教育信息化時代,有海量的試題可以給學生練習,要想在海量的試題中選擇合適的試題必須要知道學生知識點掌握情況[1,2],因此幫助教師挖掘出學生知識點熟練度是教育中急需解決的問題.

隨著計算機技術的不斷發展,傳統教育模式已經得到了很大的改變,一些教師的工作可以讓計算機去做,像試卷批改,學生知識點診斷分析等等.現有的學生知識點診斷分析大多數采用認知診斷模型[3–7],它是認知心理學[5]與教育測量學相結合的產物,主要通過學生的答題記錄來挖掘出學生的潛在信息[8],例如DINA模型[8]結合Q 矩陣[3,8]來挖掘出學生對試題所考察知識點的掌握情況,由于Q 矩陣只能給出試題考察知識點的離散化信息(即考察的知識點只有考察和未考察),因此也只能預測出學生知識點的離散化程度(即學生對知識點只有掌握和未掌握).

在實際做題過程中,知識點熟練度在0.9和1.0的情況下解決難題就可能體現出差距,這一點在數學等理科上體現的非常明顯.針對上述問題本文提出了通過特征嵌入[9]來預測學生的知識點熟練度的方法,對學生和試題分別以知識點作為特征嵌入,分別建立對應知識點的向量,并通過神經網絡[2,10,11]來訓練和調整學生知識點熟練度.

1 問題描述

無論是傳統的線下教育還是線上的智能教育[12,13],我們的最終目的都是讓學生能夠提高自己的知識能力.然而光靠課上聽講并不能完全應對考試,學生更多的還是需要課下練習試題,學生選擇的試題必須緊密結合學生自身知識點掌握情況,否則就是事倍功半,讓學生失去學習的信心.

大多數的教師在對學生知識點熟練度做出判斷時基本上按照這些要求來判定:如果學生能夠答對試題(排除猜測),說明該學生知識點熟練度是達到了試題對知識點考察的要求,甚至高于試題知識點考察要求;相反如果學生答錯該試題或者沒有拿到全部分數(排除失誤)說明該學生在試題考察的知識點上至少有一個沒有達到要求.也就是說學生知識點熟練度是可以通過答題情況來反應的,教師判斷的準確性取決于對試題考察知識點難度[14]的精準分析,因此如果在清楚試題考察知識點的難度和學生在該試題上的得分的情況下,預測出學生知識點熟練度并不難.

在教育領域中,給定學生的答題記錄為R,R中包含以下信息:學生集合D={d1,d2,…,dN},試題集合T={t1,t2,…,tM},知識點集合C={c1,c2,…cK}.每條答題記錄由(dn,tm,snm) 組成,其中snm表示學生dn在試題tm上的得分(得分已經轉化為百分比,即得分率).Q為試題關聯知識點矩陣,由相關領域專家標記,表示為Q=[qmk]M×K,qmk=1 表示試題tm考察了知識點ck,否則qmk=0.

問題定義:給定答題記錄R和試題知識點關聯矩陣Q,如何精確地預測出學生知識點熟練度.

2 學生知識點熟練度預測方法

為了解決上述問題,本文提出了一種基于特征嵌入的學生知識點熟練度預測方法FE-SKP (feature embedding-student knowledge proficiency),利用神經網絡強大的功能來捕捉學生與試題之間的關系,其中第2.1 節給出了 FE-SKP 方法的框架,第2.2 節將會介紹具體做法.

2.1 FE-SKP 框架

本節提出的FE-SKP 方法包含兩個步驟:第1 個步驟是構造嵌入模塊,其目的是構建學生和試題的知識點向量;第2 個步驟是構建網絡模型,其目的是通過輸出學生的得分預測來檢驗對其知識點熟練度預測是否準確,如果與實際得分有差距則在訓練過程中進行調整.

嵌入模塊:嵌入模塊主要包括學生知識點嵌入和試題知識點嵌入,學生知識點嵌入是將學生構建成在每個知識點上掌握程度的向量,試題知識點嵌入是將試題構建成對每個知識點考察難度的向量.構造過程如下:

1)學生知識點嵌入:首先給定一組學生的集合,嵌入模塊首先將其單獨在相應的空間下進行初始嵌入,從而獲得由固定知識點數量維度構成的學生知識點向量.我們將學生知識點向量用SnP表示,含義為學生dn的知識點熟練向量,該向量包含學生在所有知識點上的熟練度,類似于認知診斷中的學生向量,不同之處在于學生在每個知識點的熟練度都具體量化而并非離散,例如SnP=(0.1,0.5)表示該學生dn在知識點1 上的熟練度為0.1,在知識點2 上的熟練度為0.5.

2)試題知識點嵌入:試題知識點嵌入學生知識點嵌入類似,嵌入模塊首先將其單獨在相應的空間下進行初始嵌入,從而獲得由固定知識點數量維度構成的試題知識點向量,再結合Q矩陣的信息計算出試題的權重.我們將試題知識點向量用EmKnow表示,含義為試題tm考察的知識點難度向量,該向量包含試題tm在每個知識點上的考察難度.與認知診斷中Q矩陣的區別在于每個知識點并不是用1和0 表示考察和未考察,而是具體量化考察難度,例如EmKnow=(0.2,0.8)表示該試題tm對知識點1的考察難度為0.2,對知識點2的考察難度為0.8.

網絡模塊:網絡模塊主要用于檢驗學生知識點熟練度預測是否正確,由于學生知識點熟練度沒法直接給出,因此我們通過學生知識點熟練度預測他們在試題上的得分來檢驗.這里選用卷積神經網絡模型,在訓練期間,如果輸出了錯誤的預測,則優化算法會根據實際情況調整學生知識點熟練度,如果輸出正確說明學生知識點熟練度達到試題考察要求甚至還要高于試題考察要求.

2.2 FE-SKP 具體方法

(1)嵌入模塊

學生知識點嵌入:首先我們輸入學生集合D={d1,d2,…,dN},將每個學生單獨進行初始嵌入,從而獲得維度為K的序列A=(a1,a2,…,aN),操作為Emb1,Emb1和an計算方法如下:

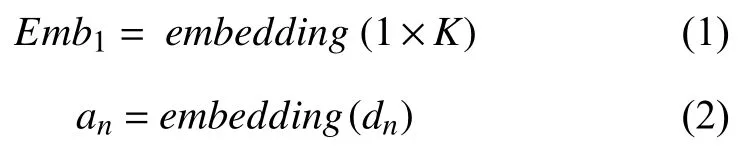
接著使用Sigmoid 函數讓學生的知識點熟練度在0–1 之間,得到學生dn知識點熟練SnP∈[0,1]1×K,SnP計算方法如下所示:

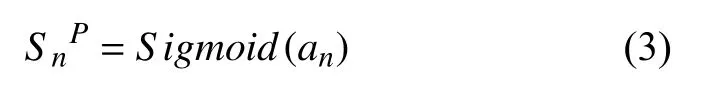
試題知識點嵌入:為了讓考察知識點的難度具體化,我們首先需要計算知識點的權重,知識點的權重計算分為兩步,第1 步是它在該試題考察的知識點中占的比重,第2 步是它在所有試題考察的知識點中占的比重.我們分別用wmk和Lk表示知識點ck在試題tm中所占的比重以及在所有知識點中所占的比重,知識點ck的權重用tck表示,如下所示:

用向量TCm=(tc1,tc2,…,tcK)表示試題tm中所有知識點的權重,接著計算每道試題難度Diffm∈[0,1],試題難度通過學生得分計算,如下所示:

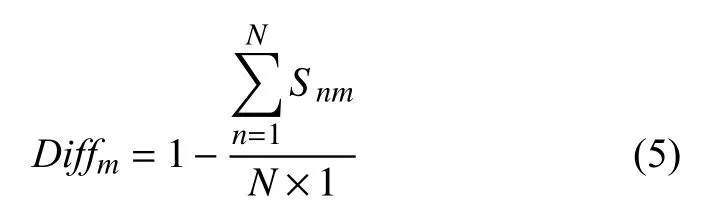
接著輸入試題集合T={t1,t2,…,tM},將每個試題單獨進行初始嵌入,從而獲得維度為K的序列B=(b1,b2,…,bM),操作為Emb1,bm計算方法如下所示:

將知識點權重向量乘以bm后,再乘以該試題難度Diffm,使用Sigmoid 函數將每個知識點難度控制在0–1 之間,最后再乘以Q矩陣得到試題tm考察知識點難度EmKnow,計算方法如下所示:

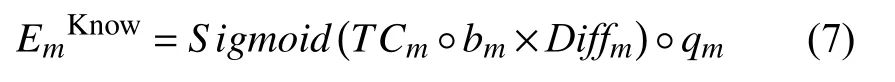
其中,EmKnow∈[0,1]1×K,qm∈{0,1}1×K,°為哈達瑪積符號.

(2)網絡模塊

該網絡模型包括嵌入層,輸入層,卷積層,池化層,全連接層和輸出層,其結構如圖1所示.

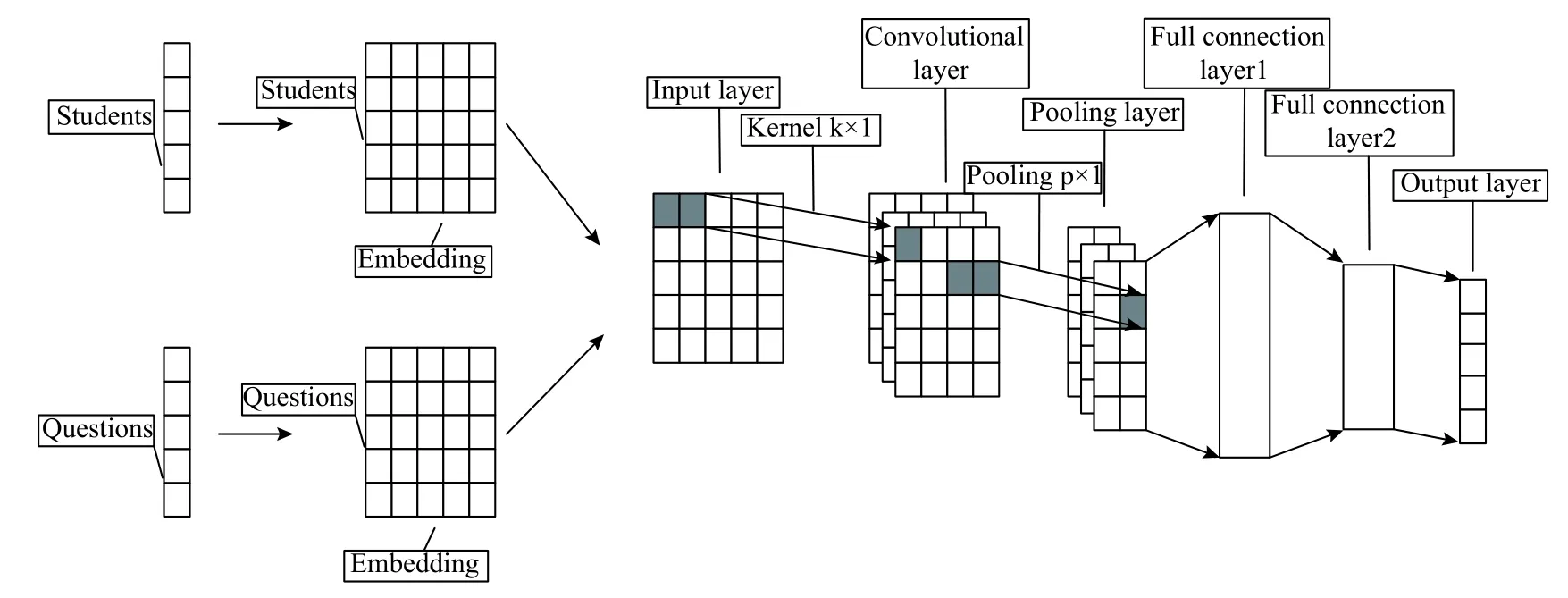
圖1 FE-SKP 方法結構

嵌入層為學生知識點熟練度SnP和試題知識點考察難度EmKnow,輸入層接受學生特征與試題特征的關系x,如下所示:

x通過卷積層執行卷積操作獲得隱藏層Hc=,j為卷積核大小;Hc經過p-max池化層得到新的隱藏層計算方法如下所示:

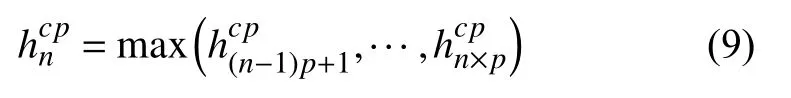
最后新的隱藏層Hcp經過兩個全連接層和一個輸出層,得到最后的得分預測y,計算方式分別如下所示:

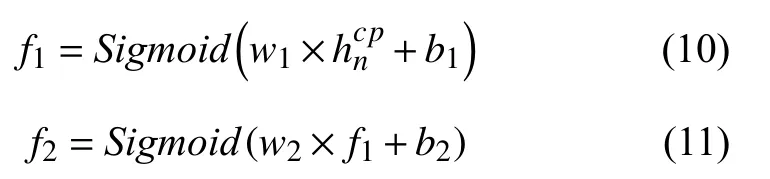
其中,w為權重參數矩陣,b為偏移量.

FE-SKP 方法的損失函數是輸出學生得分預測y和真實標簽學生實際得分s之間的交叉熵,計算方法如下所示:

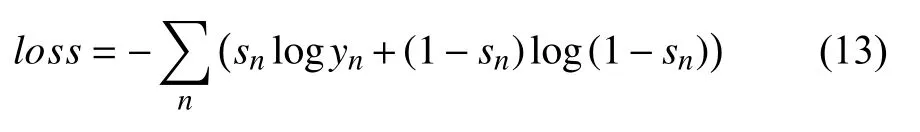
3 實驗結果分析

本節主要驗證FE-SKP 方法的有效性,其中第3.1 節介紹數據集信息,第3.2 節為數據處理過程,第3.3 節給出評價指標,最后第3.4和第3.5 節給出實驗結果并且對實驗結果進行分析.

3.1 數據集

我們使用一組真實的數據集ASSIST (ASSISTments 2009–2010 skill builder) 進行實驗,該數據集是ASSISTments 在線輔導系統收集的開放數據集,包含了學生的答題日志.每個學生答題日志學生的編號,試題編號,試題考察的知識點編號以及學生在該試題上的得分,一共有4 163 個學生,17 746 道試題和123 個知識點(每個知識點用不同編號表示,例如知識點1 表示函數),324 572 條答題日志,詳細信息如表1所示.

表1 數據集信息

3.2 數據預處理

由于我們需要輸入Q矩陣,學生和試題編號,因此我們需要將日志中的信息提取出來.首先我們將答題日志進行改進,原本是一個學生編號對應他所做的所有試題信息,我們將每條日志改為一個學生編號,一道試題信息.

接著是Q矩陣的構造,因為答題日志只有試題考察知識點的編號,因此我們需要先構造一個全為0的矩陣,維度是試題數乘以知識點數,接著將試題考察的知識點編號對應矩陣中的位置,將0 改為1 即可構造每道試題的Q矩陣.具體處理過程如圖2所示:

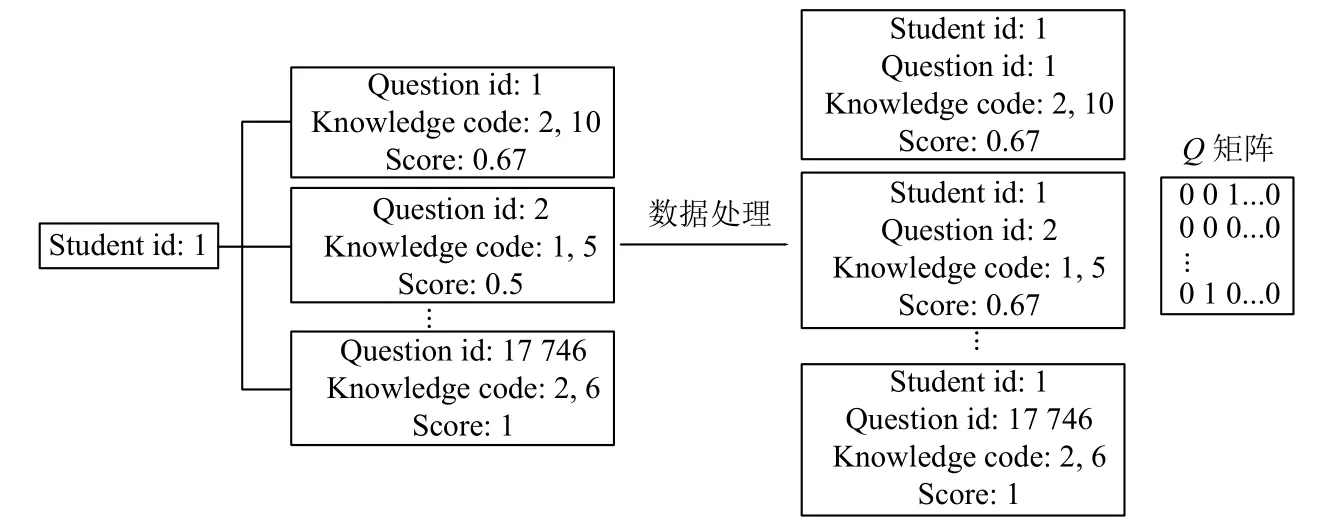
圖2 數據處理流程

最后選擇80%作為訓練集,20%作為測試集.

3.3 實驗評價指標

由于學生知識點熟練度我們無法直接判斷預測結果是否準確,因此我們通過預測學生在試題上得分來判斷知識點熟練度預測的效果.在本次實驗中,我們使用準確率(Accuracy)、均方根誤差(RMSE)、ROC 曲線下的面積(AUC)作為評價指標,其計算公式分別如下所示:

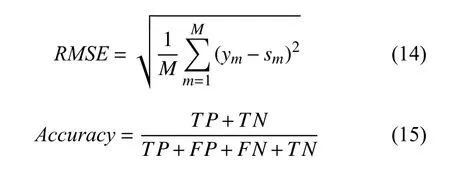
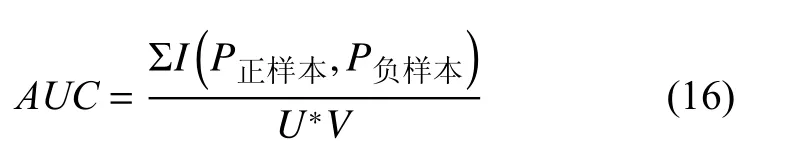
其中,TP表示正確預測學生答對試題的數量,FP表示錯誤預測學生答錯試題的數量,FN表示錯誤預測學生答對試題的數量,TN表示正確預測學生答錯試題的數量.U表示正樣本數量,V表示負樣本數量,I(P正樣本,P負樣本)計算方法如下所示:

3.4 實驗結果

為了驗證本實驗的有效性,我們對比了傳統的一些方法,其中包括認知診斷模型(DINA,IRT[15],MIRT[16,17])和概率矩陣(PMF)[18].對比方法的原理介紹如下:

DINA 方法:根據學生在每道試題上的得分情況來診斷出學生的知識狀態,其中用0 表示學生未掌握考察的知識點,用1 表示學生掌握了考察的知識點,再結合知識點關聯矩陣對學生進行得分預測.

IRT 方法:在已知試題的難度、區分度、猜測系數的情況下建立能力參數的極大似然函數,得到學生的能力參數后,通過3PL 模型計算出學生答對試題的概率.

MIRT 方法:在IRT 模型的基礎上,將學生完成一道試題需要的多種能力(即需要掌握的多個知識點)、試題特征與答對概率進行模型化.

PMF 方法:通過學生在每道試題上的得分以及試題知識點關聯矩陣,分別建立學生和試題的知識點潛在向量,假設學生和試題潛在向量服從高斯分布,通過已知的學生得分矩陣得到學生和試題的特征矩陣,用特征矩陣預測學生在試題上的得分.

介紹完對比實驗方法后,我們在該數據集上進行了實驗,結果如表2所示.

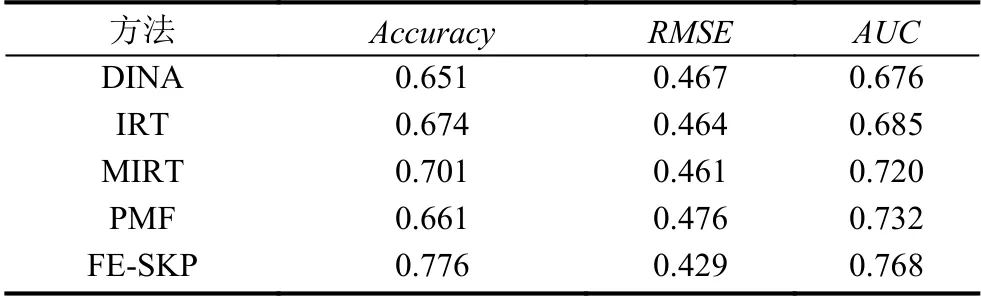
表2 實驗結果

3.5 實驗結果分析

根據實驗結果,我們可以發現FE-SKP 方法在各項評價指標中效果最好,主要原因在于以下幾點:

DINA 模型主要適用于客觀題,對于一些得分不是0 分就是滿分的題目處理的是比較好的,因為客觀題只要有一個知識點不熟練基本上就是不得分,是可以將學生的知識點熟練度視為未掌握,但是對于一些連續性得分像主觀題效果并不是很好,因為主觀題只要學生答對一個得分點就可以獲得相應的分數,DINA模型無法將學生和試題的知識點量化,在測試主觀題時只要學生有一個知識點不會該試題得分就是0 分,導致主觀題的準確率不高,均方根誤差比較大;IRT 模型認為學生的單維能力與測試得到的分數是線性關系的,但是在實際情況中往往不成線性關系,比如我們在進行考試時,想要從50 分考到60 分很容易,但是想要從90 分考到100 分卻很難,因為90 分與100 分的差距主要體現在難題上,難題涉及到的知識點非常多,并不是單個能力就能體現出來,所以在進行一些區分度大的題目上進行測試效果并不是很好;PMF 對于學生的得分預測結果缺乏一定的解釋性,因為潛在變量的維度可以任意設置,很難說明潛在變量一定是知識點,另一方面它難以融合更多的有用特征,例如像試題知識點的考察難度.因此,這3 種傳統的方法的效果并不是很理想.

相對于傳統的3 種方法,MIRT的效果還是比較好的.MIRT 相對于IRT的區別主要是潛在向量的建模,IRT 潛在向量是一維的,而MIRT 潛在向量是多維,即一道試題會測試K種能力,而學生在做這道試題時最后的得分對應了K種能力,但是仍然存在IRT 模型中能力與得分線性關系的缺陷.而FE-SKP 方法利用了卷積神經網絡強大的擬合能力,提取更具有決定性的特征,使其能夠捕捉到學生與試題之間的關系,并且在構建試題知識點嵌入是考慮了試題考察的知識點權重以及試題的難度,提高了預測試題知識點考察難度的準確性,從側面提升了學生知識點熟練度預測的準確性和分類效果,并且能夠減少均方根誤差.

4 結論與展望

本文將知識點作為特征嵌入到學生與試題之中,并且通過卷積神經網絡來捕捉學生與試題之間的聯系,從提升試題知識點考察難度準確率來增加學生知識點熟練度預測的準確率.雖然較傳統方法上準確率有所提高,但是準確率并沒有達到教育上完美要求,教師面對的是一個班級甚至是幾個班級的學生,對每個學生都需要負責.因此希望在后面的工作中,可以繼續提升準確率,大大減輕教師和學生的壓力.