小行星動能防御精確相對導航與制導方法研究

普渝皓，程實，陳楊*

(1.航天科工空間工程發展有限公司，北京100854；2.中國航天科工集團二院研究生院，北京100854)

1 引言

近地小行星對地球的威脅持續存在，特別是大量未發現編目的近地小行星對地球持續造成嚴重突發撞擊威脅。從歷史情況看，直徑1km以上小行星撞擊地球概率較低且短期內難以有效防御，直徑10m以下小行星危害較小無需針對性進行防御，因此監測預警的重點目標為直徑10m至1km的近地小行星。進一步考慮工程可行性、應對必要性等因素，防御任務重點為直徑十米級至百米級的小行星。近年來，小行星防御技術成為研究熱點，其中任務末段的相對導航技術與制導技術是關鍵技術[1]。

“雙小行星重定向測試”(Double Asteroid Redirection Test, DART)任務于北京時間2022年9月27日，對Didymos雙小行星系統中直徑160m的次星Didymos B進行動能防御，仿真命中點距瞄準點約15m[2]，實際命中點距離圖像中心17m。根據公開報道，DART任務主飛行器經過深空機動與多次中制導修正，滿足中末交接班條件后，進入末制導階段，在此階段使用源于比例引導的制導律，制導算法使用擴展卡爾曼濾波(Extended Kalman Filter, EKF)對交會時刻的投影脫靶量進行估計[3]。濾波器的觀測量是由圖像解算出的慣性坐標下的視線角，并且假設任務飛行器與目標小行星之間無相對加速度。根據投影脫靶量大小進行修正，在交會前5min進行連續修正，并在交會前2min停控，準確命中目標小行星。面對目標尺寸更小、目標軌道預報精度更低、交會精度要求更高的任務場景，上述方法還有改進的空間。

首先，考慮提升濾波算法的精度。以視線角為觀測量的相對導航系統是典型的非線性系統。EKF算法在線性化過程中忽略了非線性函數泰勒級數展開的二階及以上的高階項。在初始誤差較大的情況下，特別是在目標軌道預報精度較低的情況下，有可能引入較大的線性化誤差。無跡卡爾曼(Unscented Kalman Filter, UKF)算法不需要對狀態方程和觀測方程線性化，沒有對模型高階項的截斷誤差，可以獲得比EKF更好的估計精度和濾波穩定性[4]。EKF和UKF算法均需要已知系統噪聲和觀測噪聲的統計特性。噪聲統計特性的偏差將導致濾波精度下降甚至導致濾波發散。為了克服這一問題，需要引入在線估計噪聲統計特性和修正濾波增益的自適應濾波技術，如基于協方差匹配的自適應濾波[5]、基于極大似然方法的自適應濾波[6,7]和基于模糊邏輯的自適應濾波[8,9]等。

其次，考慮提升制導指令的計算精度。在公開文獻中，DART任務在進行投影脫靶量估計時，忽略了相對加速度對制導精度的影響[2]。根據Lorenzo F的研究表明，DART任務在四體動力學環境下引起的軌道誤差均值為238m，目標軌道不確定性引起的平均軌道誤差為10m[10]。因此，為應對更小尺寸小行星的更高精度的防御場景，在投影脫靶量的估計時，需要考慮復雜引力環境產生的相對加速度。

本文首先以B平面坐標系作為相對導航坐標系，并給出該坐標系下的自主相對導航系統模型。其次將適用于線性系統的Sage-Husa噪聲估計器推廣到非線性系統，結合UKF算法得到一種自適應無跡卡爾曼(Adaptive Unscented Kalman Filter, AUKF)濾波器，并引入協方差匹配的思想，進一步提高濾波的快速性和穩定性。在投影脫靶量的估計計算中，考慮復雜引力環境下的影響，提出一種利用投影脫靶量直接計算制導指令的制導方法。最后以具有潛在威脅的小行星Bennu為目標，設計典型任務場景并生成飛行數據，對本文提出的模型及算法進行仿真驗證。

2 自主相對導航方法

2.1 系統模型

2.1.1相對導航坐標系

本文考慮單目僅測角相對導航系統，以目標天體的俯仰角和方位角為觀測量。任務末段飛行器相對目標天體的位置矢量和速度矢量夾角很小，甚至重合，沿視線方向的信息無法通過連續觀測獲得。若在J2000日心黃道坐標系中描述狀態方程，視線方向距離無法估計的特性將反映到三個慣性坐標軸上，導致三軸的位置估計均不可信，無法保證三軸的位置信息的估計精度。因此，需要將沿視線方向的距離獨立出來，提高垂直于視線方向的估計置信度。

B平面坐標系是根據任務飛行器相對目標天體進入漸近線方向定義的參考坐標系，如圖1所示，其數學定義為：以目標天體為中心原點，S軸為進入軌道雙曲線漸近線的方向矢量，某參考方向矢量記為N，S與N叉乘作為T軸，R軸由S軸和T軸按右手螺旋法則確定。在本文中，S矢量方向可選為初始時刻任務飛行器相對目標天體的速度V∞的方向。取N為任務飛行器軌道平面的法線。即：

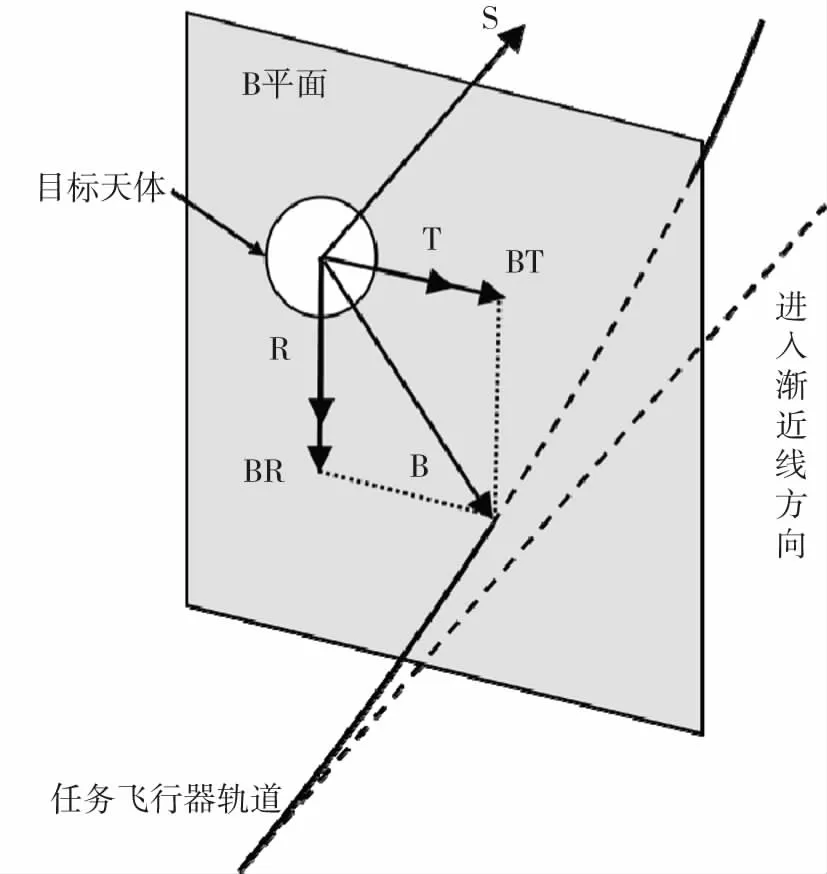
圖1 B平面坐標系示意圖

(1)

式中：r和v分別表示任務飛行器在慣性系下的位置和速度矢量。則B平面坐標系慣性坐標系的轉換矩陣為：

(2)

視線方向與相對位置方向重合，相對位置方向和相對速度方向幾乎重合。因此B平面坐標系可以將視線方向的距離獨立出來。由于S軸近似表示飛行器進入B平面的方向，T軸和R軸方向的位置信息可以描述任務飛行器與小行星在B平面內的相對位置。故選取B平面坐標系作為相對導航坐標系。

2.1.2 系統狀態和觀測方程

該任務的中心天體為太陽，同時飛行器與小行星還要受其他大行星引力及太陽光壓力等攝動力的影響。飛行器在接近目標天體的末段，其與目標天體所處的位置相差不大，二者所受的太陽引力、攝動力相差很小。在不進行機動時，任務飛行器相對目標小行星近似做勻速直線運動。由于近似所忽略的加速度可視為系統狀態噪聲。任務飛行器在B平面坐標系下的離散系統狀態方程為：

(3)

式中：X=[xyzvxvyvz]T表示任務飛行器在B平面坐標系下的相對位置和速度；t表示濾波步長，Wk-1表示系統狀態噪聲。

假設光學相對導航相機捷聯安裝在任務飛行器本體，輸出在飛行器本體坐標系下描述的目標視線角，包括俯仰角和方位角。因此觀測模型如下：

(4)

式中：qγ和qλ分別表示目標的俯仰角和方位角；Vk表示觀測噪聲；xb、yb、zb表示r在本體坐標系b系下的投影。xb、yb、zb與系統狀態x、y、z的轉換關系為：

(5)

2.2 AUKF濾波算法

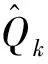
假定非線性系統的狀態方程和觀測方程具有離散形式，可表示為：

(6)

式中：X表示被估計的隨機向量，Z表示對X的觀測為隨機向量，f和h表示非線性向量函數，Wk和Vk表示不相關的噪聲序列，且Wk和Vk滿足：

(7)

式中，δkj表示Kronecker算子。

針對線性系統，Sage和Husa提出了基于極大后驗估計的噪聲統計估值器[11]。將此噪聲統計估值器推廣到非線性系統，可以得到式(6)對應的非線性時變噪聲統計無偏遞推估值器為：

(8)

(9)

(10)

(11)

(12)

(13)

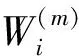
基于無跡卡爾曼濾波算法，結合式(8)～(11)所示的Sage-Husa噪聲統計估值器以及協方差匹配思想，可以得到自適應無跡卡爾曼濾波算法。針對式(6)所示的非線性系統，本文提出的自適應無跡卡爾曼濾波算法實現步驟如下：

步驟1，選定濾波初值

(14)

(15)

(16)

(17)

對k=1,2,3…，執行：

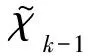
(18)

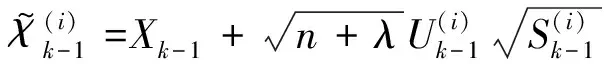
i=1,2,…,n

(19)

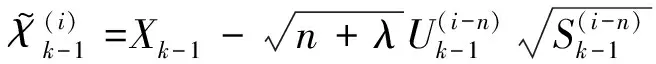
i=n+1,n+2,…,2n

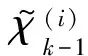
(20)

步驟3，時間更新

(21)

(22)

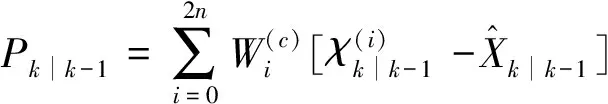
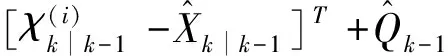
(23)

步驟4，觀測更新

(24)

(25)

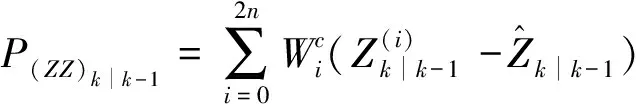
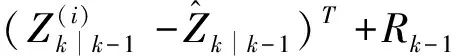
(26)

(27)

步驟5，狀態更新

(28)

(29)

(30)

式(28)表示狀態增益矩陣更新；式(29)表示狀態變量值更新；式(30)表示狀態誤差方差陣更新。

步驟6，噪聲更新

需要特別指出的是，當系統噪聲方差陣Q和觀測噪聲方差陣R均未知時，由于無法從輸出中區分系統噪聲和觀測噪聲造成的影響，Sage-Husa噪聲估計器無法同時對二者進行估計[12]。因此，需要在一種噪聲已知的條件下估計另一種噪聲。本文對飛行器相對目標小行星的運動采取了近似處理，忽略的相對加速度為系統噪聲，且系統噪聲為時變噪聲，而觀測噪聲與敏感器的精度和安裝有關，可以預先確定。故本文對系統噪聲進行估計：式(8)表示對系統噪聲均值的估計；式(10)表示對系統噪聲方差的估計。

步驟7，濾波發散抑制

協方差匹配的基本原理是：檢驗殘差與其理論統計特征的相容性，即在濾波過程中，判斷殘差的統計分布在原假設條件的相容性，當殘差在原假設下不相容，則需要根據殘差與理論統計特征一致的原則，對協方差陣進行修正。

根據協方差匹配判據，濾波器收斂時應滿足：

(31)

式(31)中，εk表示殘差序列；γ為事先設定的可調系數，取值范圍為γ≥1;tr[·]表示求跡運算。若式(31)不成立，則對Pk∣k-1做如下修正：

(32)

式(32)中，λk的確定規則如下：

(33)

(34)

(35)

式(35)中，μ表示衰減系數，取值范圍為0<μ≤1，一般取值為0.95。該系數能進一步提高濾波器的快速跟蹤能力。當增大μ時，k時刻之前信息所占的比重減小，當前殘差的影響增大。由于沿視線方向的分量是不可觀測的，因此在進行修正時，沿視線方向的分量不進行修正。該方法有很強的關于突變狀態的跟蹤能力，并且在濾波達到穩態時，仍保持對于緩變以及突變狀態的跟蹤能力。

綜上所述，AUKF濾波器計算流程圖如圖2。

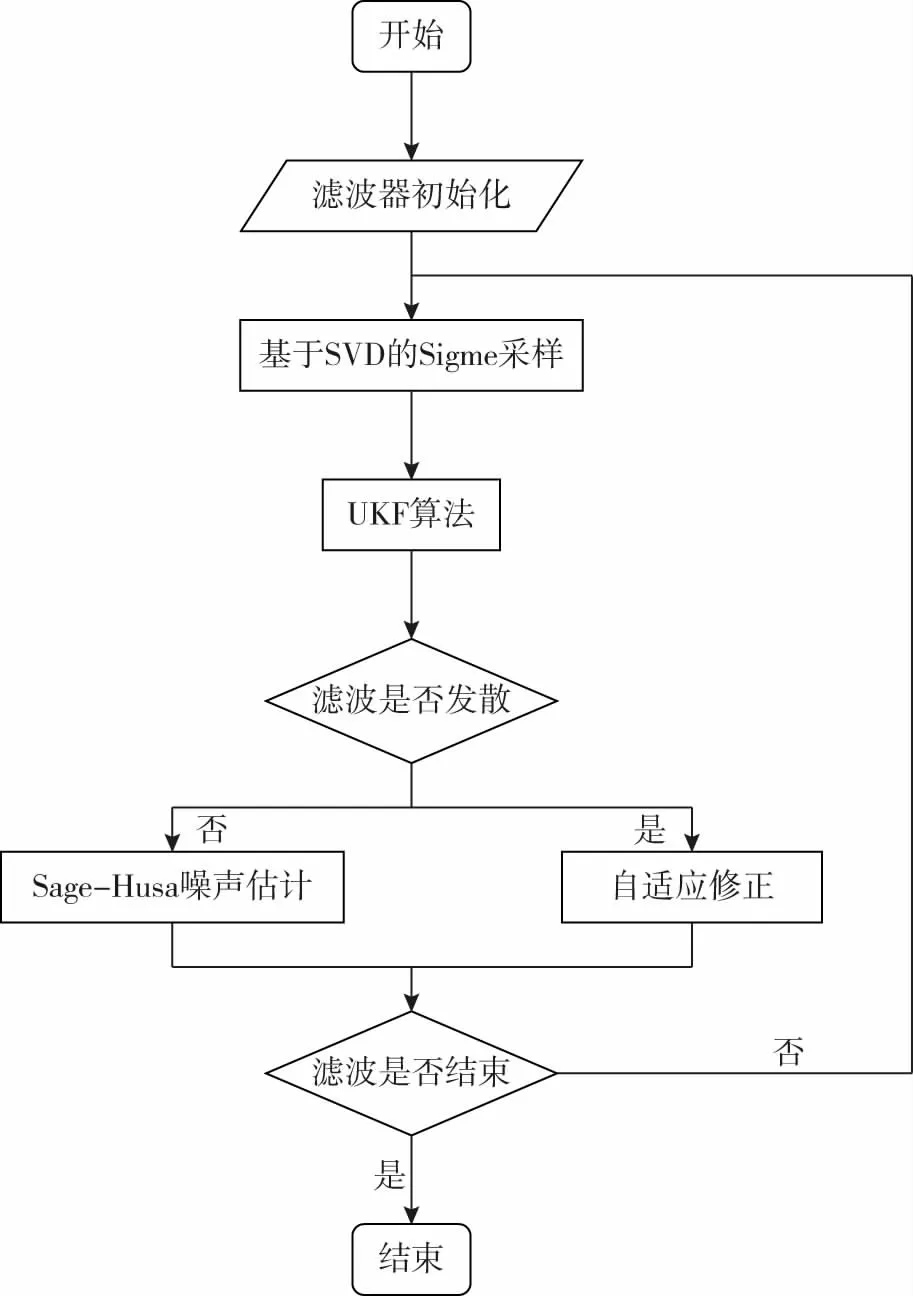
圖2 濾波器計算流程圖

3 投影脫靶量制導

3.1 投影脫靶量常值模型估計與計算

根據任務飛行器深空自主導航和相對導航結果，能夠確定當前時刻任務飛行器與目標小行星在慣性空間的位置與速度，進而可以確定兩者的引力加速度GT、GI和飛行器與目標小行星之間的引力差GT/I。針對交會過程的末制導段，交會時刻的引力差很小，即GT/I=0。因此，當前時刻引力差常值模型用式(36)表示：

(36)

式中：ti表示當前時刻，tf表示交會時刻。由式(36)可知，雖然投影脫靶量的計算是一個常數，但是在每次制導計算過程中，通過C0更新來反映當前的引力狀態。將式(36)帶入的式(37)中且令控制力F=0，并對其進行積分：

(37)

VT/I(t)=C0(ti)(t-ti)+VT/I(ti)

(38)

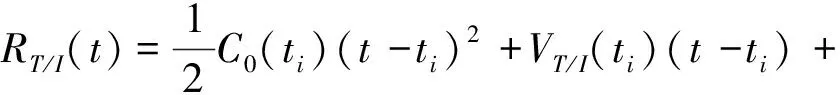
RT/I(ti)

(39)

式中，aT/I、VT/I(t)和RT/I(t)分別表示飛行器與小行星的相對加速度、相對速度和相對位置。

飛行器與小行星的相對距離到達最小值時，應滿足的條件是:

VT/I(t)·RT/I(t)=0

(40)

將式(38)和式(39)帶入式(40)后得到以交會時間為未知量的方程如下所示：

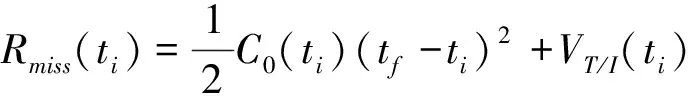
(tf-ti)+RT/I(ti)

(41)

式(41)中，Rmiss(ti)表示ti時刻的投影脫靶量(Projected Miss Distance)。根據式(36)-式(41)，當C0為0的時候常值模型下的投影脫靶量表達式與不考慮相對引力影響的表達式完全一致。另外，式(41)中通過C0引入了用于表達不同引力的高階項，使得表達式能夠更加準確的近似表達引力差的二次項。

3.2 制導律

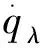
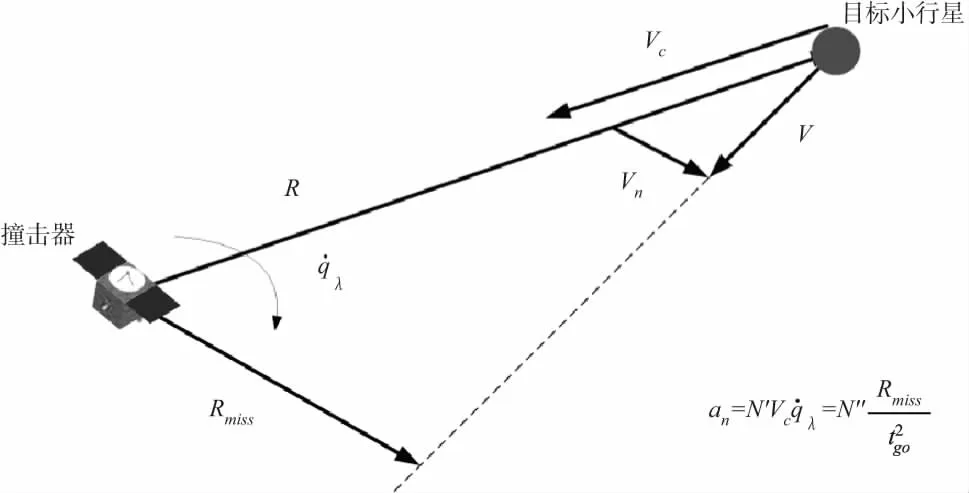
圖3 比例導引與投影脫靶量的關系

從圖3中可以看出，投影脫靶量還可以表示為：

(42)

(43)

比例導引法是根據飛行器的旋轉角速度與目標視線角速度成正比得出的一種導引方法。廣義比例導引是針對比例導引的一種改善形式，其一般形式為

(44)

將式(43)帶入式(44)，可以得到基于投影脫靶量的制導指令計算形式：

(45)

令tgo=tf-ti，式(45)可以簡化表示為：

(46)

上述給出的過載指令均為連續變大小控制量，考慮飛行器無法產生連續可變的制導過載，需要設計高精度的控制輸出變換方法，通過脈寬調制等手段生成離散開關控制量，驅動推力器完成實際的推力輸出。采用脈沖調寬調頻方法(PWPF)，對推力指令進行分配。對于PWPF中的4個參數：放大系數、時間常數、推力器的開關閾值，在實際應用中，通過試湊的方法經仿真試驗來確定。

4 仿真實驗及分析

4.1 仿真場景

基于潛在威脅小行星Bennu構建小行星防御典型場景，進行仿真驗證。Bennu開普勒軌道信息如表1所示[13]。以軌道信息標稱值設計飛行任務，任務于2036年9月18日0時開始，交會時間為2037年1月16日0時，交會前4h進入末段導航與制導階段。小行星實際軌道根據星歷誤差范圍隨機選擇，小行星直徑選擇為30m。為驗證算法在實際應用中的有效性，除星歷誤差外引入多種誤差源，進行蒙特卡洛仿真分析，誤差項及數值如表2所示。

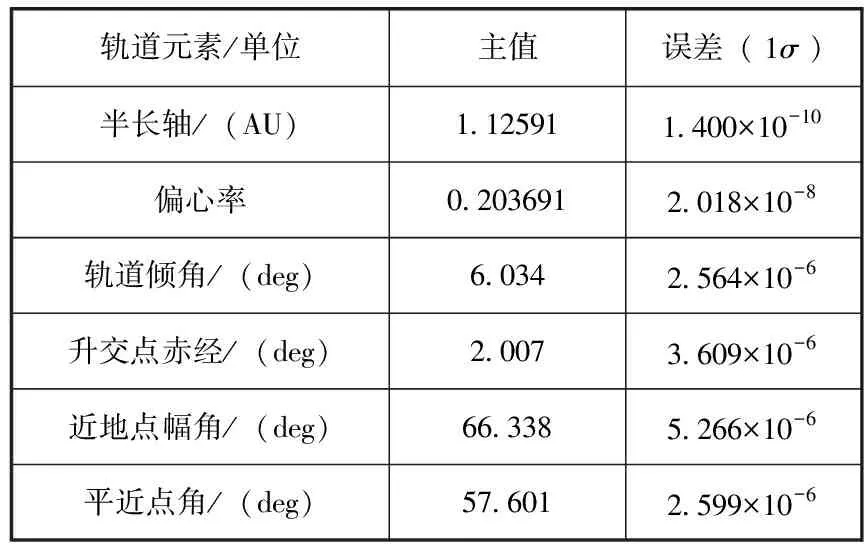
表1 Bennu開普勒軌道信息(時間：59000.0 MJD)

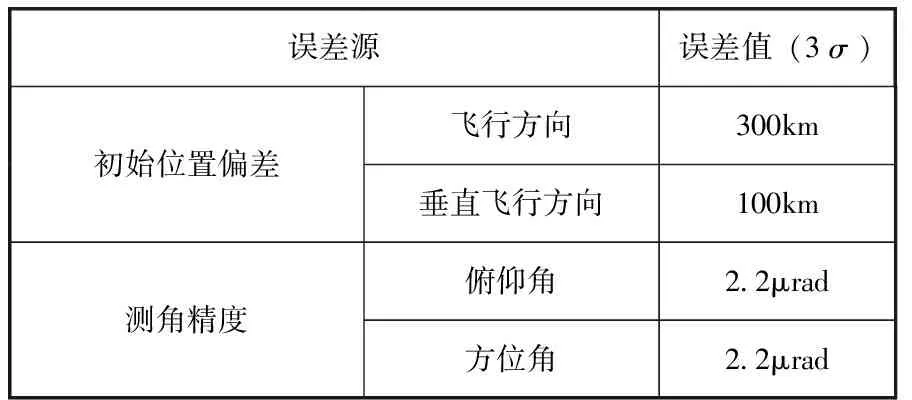
表2 誤差源及誤差值

4.2 仿真結果與分析

為對比本文提出的算法與其他算法的相對導航效果，在不施加機動的情況下，分別采用EKF算法、UKF算法、不含協方差匹配的AUKF算法以及含協方差匹配的AUKF算法(本文提出的完整算法)進行仿真。目標小行星在J2000日心黃道坐標系的初始位置為[-50119639522.77，130393530773.86，13960229459.83]m，初始速度為[-32208.87，-8047.33，-730.88]m/s，任務飛行器的初始位置為[-50183158838.61，130466720546.96，13974363604.73]m，初始速度為[-27784.43，-13118.19，-1716.38]m/s。在計算濾波器的初值時，目標小行星的初始位置和速度由小行星星歷主值計算得出，任務飛行器的初始位置和速度根據真實位置設置測控誤差，誤差大小如表2所示。本文中采用的濾波初值為[-97946239.90，-241607.05，88444.30，6801.47，0.00，0.00]。濾波器的參數設置一致。系統狀態噪聲方差陣Q0=diag(1×105,1×105,1×105,1×102,1×102,1×102)，觀測噪聲方差陣R0=diag(6×10-8,7×10-8)，初始狀態誤差方差陣P0=diag(1×108,1×106,1×106,1×102,1×102,1×102)，濾波步長為5s，其他參數按上文推薦取值給定。由于飛行器沿視線方向不可觀測，在濾波不發散的情況下，該方向的位置和速度的變化趨勢與按照初始值遞推一致。故僅列出Y軸和Z軸方向的濾波結果，如圖4、5所示。

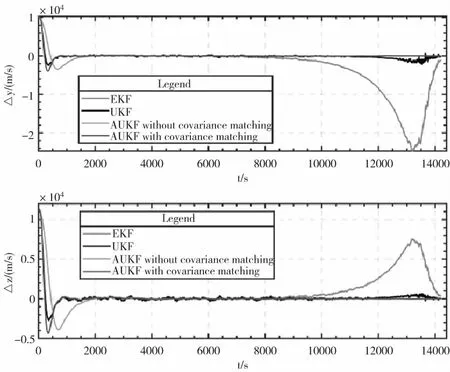
圖4 B平面坐標系下位置估計誤差

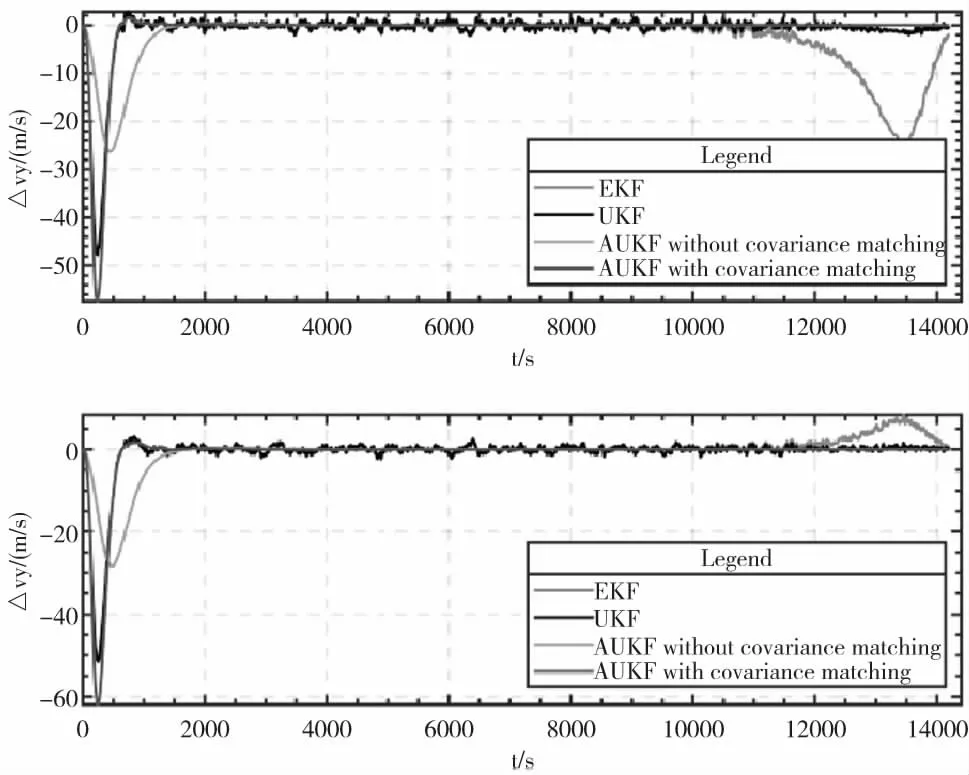
圖5 B平面坐標系下速度估計誤差

由圖4、5可以看出，EKF算法隨著濾波時間的增加，累計的誤差變大，出現了發散的情況；UKF算法由于預先給出的噪聲統計特性存在偏差，估計精度較差；引入噪聲估計器后，濾波精度提高，但是收斂速度變慢；利用協方差匹配的思想進行修正，濾波收斂時間從約2000s減小至約1000s。交會前300s，y、z方向的位置濾波誤差為6.89m和0.19m，速度濾波誤差為0.0016m/s和0.00028m/s。本文提出的相對導航算法具有快速、高精度的特點。

在上述條件下對本文給出的僅測角導航模型相對導航和投影脫靶量制導算法進行仿真驗證，飛行器質量800kg，推力大小為5N，交會前兩分鐘停止控制。制導過程中，B平面坐標系下垂直于視線方向的投影脫靶量的估計值和真實值變化如圖6所示。進行200次蒙特卡羅仿真驗證，最終交會誤差散布圖如圖7所示。最終交會誤差的均方差3σ=5.22m，最大交會誤差為6.3m。

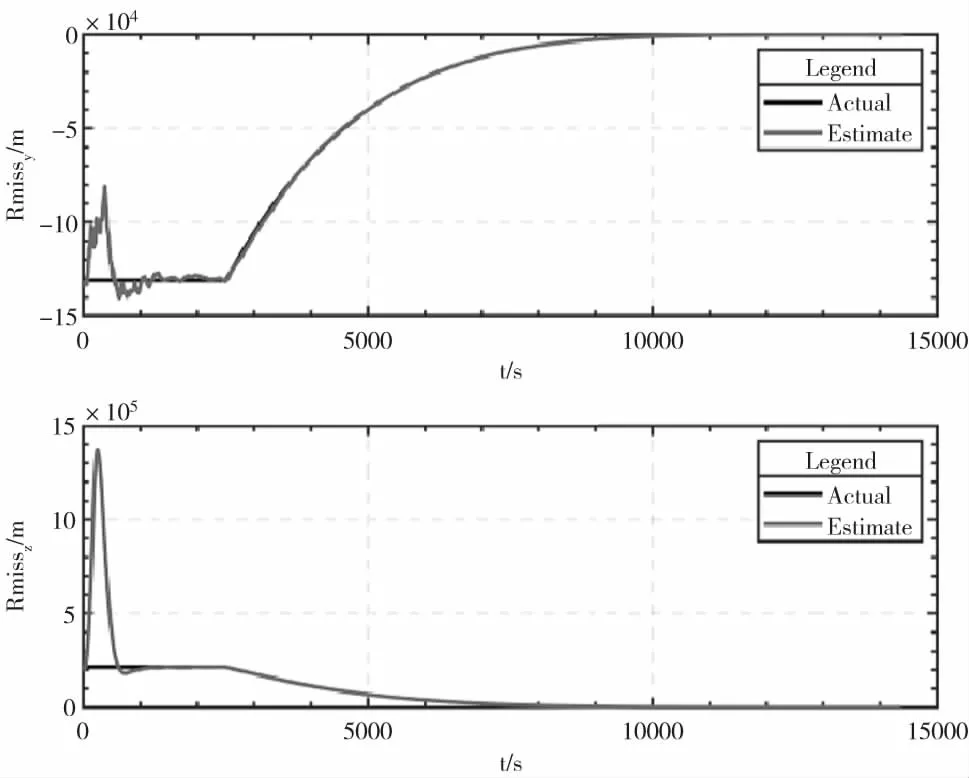
圖6 末制導階段飛行器與導航濾波器表現情況

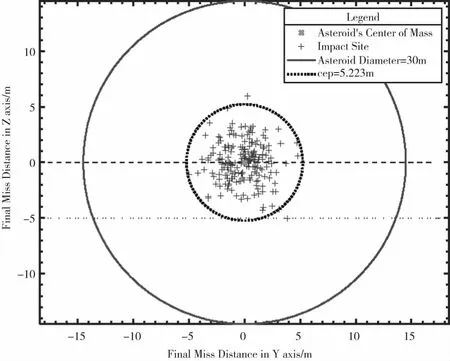
圖7 B平面內命中點散布圖

5 結論

小行星防御中的目標尺寸更小、目標軌道預報精度更低、交會精度要求更高等問題對相對導航的估計精度和制導精度提出了更高要求。本文首先采用B平面坐標系作為相對導航坐標系，分離出不可觀的信息，建立僅測角導航的系統狀態方程及觀測方程。由于觀測方程為非線性方程，本文以UKF算法作為基礎濾波算法，避免了線性化后帶來的截斷誤差。考慮系統方程含有未知統計特性的噪聲，將Sage-Husa噪聲估計器推廣到非線性形式，對未知噪聲進行在線估計。針對Sage-Husa算法對濾波穩定性及快速性帶來的影響，采用協方差匹配思想和奇異值分解方法，加快濾波收斂，提高濾波的穩定性并且保證算法不失效。其次利用相對導航濾波結果，建立了引力差產生的相對加速度的常值模型，計算考慮相對加速度的投影脫靶量，并設計了基于投影脫靶量的制導指令計算方法。最后利用典型小行星防御任務場景進行算法精度驗證。由計算機仿真結果表明，本文建立的模型及濾波算法可以對可觀測坐標軸方向的狀態進行快速準確估計。基于投影脫靶量的制導算法，在復雜引力環境下，能夠實現5.22m(3σ)的交會精度。本文的相關研究，能夠為我國未來小行星防御任務相對導航與制導系統的設計提供一定的參考和理論依據。