動能撞擊偏轉小行星的動量傳遞效率數值仿真研究

陳鴻，李毅，鄒勝宇，周浩

(中國空氣動力研究與發展中心超高速碰撞研究中心，綿陽 621000)

1 引言

小行星撞擊地球可能導致全球范圍內的地震、海嘯、火山、惡劣氣候等災害，是人類未來面臨的潛在危險之一。動能撞擊和核爆炸[1]是當前技術條件下使小行星偏離原軌道的兩種可行方法，其中，動能撞擊方法具有技術成熟和成本低的優點，是應對小尺寸小行星撞擊風險的首選手段。衡量動能撞擊偏轉效率的一個重要指標是動量傳遞效率，通常采用動量傳遞因子β表示，其定義為目標小行星獲得的動量與撞擊體動量之比。動量傳遞效率與撞擊體尺寸、密度、相對速度、目標小行星材料特性和組成結構等諸多因素相關。研究機構和學者開展了大量地面試驗研究[2-8]，獲得了多種材料在超高速撞擊條件下的動量傳遞因子，但地面試驗仍然有兩項局限性：一是地面試驗材料與真實的小行星材料有差異，二是地面試驗的尺度有限。為評估動能撞擊偏轉小行星可行性，NASA和歐洲航天局(ESA)聯合開展了AIDA(Asteroid Impact and Deflection Assessment mission)小行星撞擊偏轉評估任務[9-12]，旨在通過真實的撞擊，觀測評估動能偏轉效率，驗證地面試驗和數值仿真方法。在AIDA任務中，NASA已于2022年9月27日實施了DART(Double Asteroid Redirection Test)試驗，這是首個針對近地小行星的撞擊偏轉試驗。DART試驗撞擊的目標是Didymos(迪迪莫斯)雙星系統中的Didymos-B(迪莫弗斯)小行星，觀測結果表明該小行星為松散的石質小行星[10, 11]，孔隙率和拉伸強度是松散石質材料的主要力學屬性，因此，本文采用數值仿真方法研究孔隙率和拉伸強度對動量傳遞效率的影響。根據地面開展的動量擺試驗，利用自主研發的基于歐拉網格的沖擊動力學仿真軟件NTS[13]開展數值仿真，驗證數值仿真方法的可信度，在此基礎上基于DART試驗計劃開展小行星動能撞擊偏轉過程仿真，分析孔隙率和材料拉伸強度對動能轉換效率的影響。

2 數值仿真方法

對小行星的撞擊偏轉屬于超高速碰撞范疇，涉及高溫、高壓、大變形、材料斷裂和破碎問題，一般采用歐拉方法和無網格方法開展數值仿真研究。在小行星撞擊問題中，撞擊器的尺寸遠小于小行星尺寸，網格/粒子尺寸由最小尺寸部件決定，若采用三維數值仿真，則在保證計算精度的前提下，必然導致網格規模過于龐大，對計算資源和時間需求過高。基于以上考慮，本文采用軸對稱歐拉方法開展數值仿真。仿真計算中，采用基于自適應歐拉網格的碎片識別算法識別撞擊反濺碎片[14]，再根據每個反濺碎片的動量計算小行星的動量增量。由于Didymos-B小行星質量較小，在本文計算中不考慮引力作用。

一般情況下，為達到較好的偏轉效果，撞擊器與小行星相對速度較高，撞擊器和小行器材料會發生氣化現象，因此需要采用包含相變的狀態方程。本文的計算中，撞擊器和小行星均采用Tilotson狀態方程，參數見表1，參數定義見文獻[15]。

表1 AL2024和花崗巖狀態方程參數

在本文的仿真中撞擊器材料為AL2024，小行星材料采用不同孔隙率的花崗巖代替。金屬材料在超高速碰撞下通常會產生軟化效應，因此對于撞擊器采用Steinberg強度模型。

Steinberg本構模型忽略應變率效應，將材料分為熔化前和熔化后兩種狀態，在熔化前材料的剪切模量和屈服強度分別如下：

(1)

(2)

式中：G為剪切模量，Y為屈服應力，p為壓力，v為體積，T為溫度，ε為有效塑性應變，β、n為常數，下標0對應初始值，下標p、T對應參考值。熔化后材料強度直接降為零。

Al2024 Steinberg本構參數見表2。

表2 AL2024 Steinberg本構參數

花崗巖屬于脆性材料，而脆性材料本構通常較復雜，需要較多的經驗參數，在缺少相關參數的情況下，本文采用彈塑性模型和von Mises屈服準則。碰撞成坑過程中的反濺碎片主要由沖擊波在自由面反射形成的拉伸作用和材料的塑性流動形成，因此采用拉伸破壞模型來模擬花崗巖的材料失效。主要參數見表3。

表3 花崗巖本構參數

采用P-α模型[16-18]來模擬花崗巖的孔隙率。在P-α模型中，α為材料膨脹率，其定義為：

(3)

式中：ρS為基體材料密度，ρ為孔隙材料密度。P-α模型的基本假設是，孔隙材料的壓力與基體材料壓力呈線性關系，內能與基體材料相同，即

(4)

α僅與壓力P有關。在本文仿真中采用以下形式的函數。

(5)

式中：Pe為材料處于彈性和塑性分界點時的壓力，PS為孔隙完全壓實即孔隙率為0時的壓力。在本文仿真中Pe為1MPa，PS為213MPa。

3 數值方法驗證

為確保數值仿真結果的可信度，對已開展的彈道擺試驗[12]進行數值仿真對比驗證。彈道擺試驗在彈道靶設備中開展，通過發射彈丸超高速撞擊采用鋼絲懸掛的靶材，根據靶材的擺動測試動量傳遞因子。采用兩種方法測量靶材速度：一是速度法，即根據高速攝影圖像分析測量碰撞后靶體質心的平移速度；二是擺角法，即根據彈道擺擺動角度計算靶體在最低點的動能計算靶體平移速度。彈丸為球形鋁彈丸，靶材為花崗巖材料，靶材尺寸為110mm×110mm×100mm。撞擊參數見表4。采用軸對稱模型開展數值仿真，網格尺寸為0.1mm，模擬時長為500μs。

表4 動量擺試驗數據及數值仿真結果

在數值仿真中，以撞擊點位置垂直速度方向的平面為基準面，計算過程中對通過基準面的反濺碎片的動量進行累加，直至靶材達到穩定狀態，再根據反濺碎片動量計算靶材動量。圖1是仿真獲得的靶材動能變化曲線，靶材在撞擊瞬間獲得較多動能，此后迅速衰減，到碰撞后300μs之后基本保持不變，可認為300μs之后，靶材速度達到穩定狀態，即動量不再變化。仿真計算中采用500μs的模擬時間，可確保此時靶材達到了穩定運動狀態。圖2是動量擺試驗和數值仿真獲得的動量傳遞因子對比。數值仿真獲得的動量傳遞因子與采用速度法測量結果較接近。由于花崗巖斷裂的隨機性，試驗結果具有一定的隨機波動范圍，而數值仿真中未引入隨機因素，因此計算得到的動量傳遞因子隨碰撞速度增加而單調提高[19]。

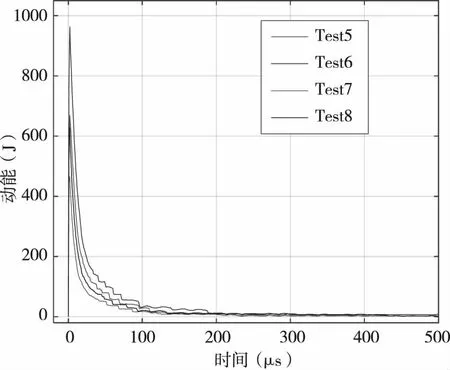
圖1 碰撞過程中靶材動能變化曲線(test5)

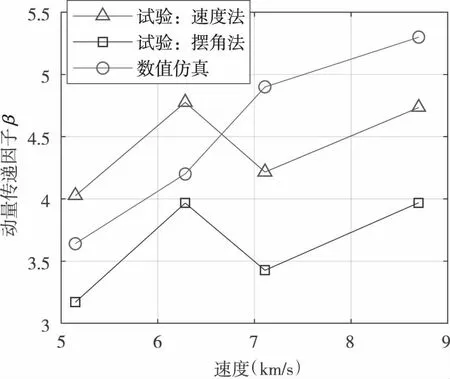
圖2 不同工況下動量傳遞因子對比

4 小行星動能撞擊偏轉仿真

DART試驗撞擊的Didymos-B小行星為近似橢球體形狀，直徑約為160m，為便于計算，將Didymos-B小行星簡化為直徑160m的均質球形小行星。Didymos-B小行星為碎石堆結構，由巖石塊和基體材料組成，目前無法通過觀測手段獲得其孔隙率和材料拉伸強度。由于基體材料結合力較弱、孔隙率高，參考典型土壤，假定拉伸強度為5kPa，孔隙率為20%；巖石塊拉伸強度較高、孔隙率低，參考典型巖石，假定拉伸強度為300kPa，孔隙率為0%～5%。因此，在仿真中拉伸強度范圍為5～300kPa，孔隙率范圍為0%～20%。

DART試驗設計的撞擊器質量約600kg，設計撞擊速度約6.1～6.6km/s。考慮燃料消耗，在仿真中撞擊器簡化為直徑0.61m、長0.61m的鋁合金圓柱體，質量為496kg，撞擊速度取6.6km/s。NASA于9月27日實施了DART試驗，據報道實際撞擊器質量約570kg，撞擊速度約6.1kg，本文工作在DART任務實施前完成，計算中采用的撞擊器質量和撞擊速度與實際情況有一定的差異。

圖3是沿撞擊方向設置的觀測點在撞擊過程中的最大沖擊壓力曲線。在撞擊初始階段，非孔隙材料對應的最大沖擊壓力高于孔隙材料。在距離撞擊點0.2～1m范圍內，非孔隙材料和孔隙材料對應的最大沖擊壓力基本一致。在距離撞擊點1m以外，非孔隙材料對應的最大沖擊壓力隨距離衰減速度明顯低于孔隙材料。分析其主要原因為：在撞擊初期，由于撞擊器速度較快，孔隙能夠較快從壓縮階段轉為壓實階段，因而對應位置的孔隙材料最大沖擊壓力與非孔隙材料的最大沖擊壓力基本一致；隨著侵徹深度增加，撞擊器速度變慢，孔隙從壓縮階段向壓實階段轉變速度變慢，從而導致對應位置的孔隙材料最大沖擊壓力比非孔隙材料有明顯的衰減。

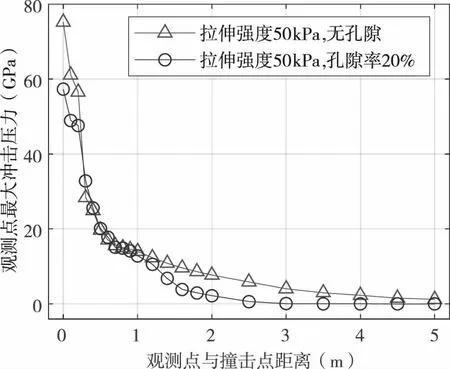
圖3 沿撞擊方向觀測點最大沖擊壓力曲線

圖4是典型仿真工況下的撞擊坑形態。在相同孔隙率下，材料拉伸強度越低，則撞擊坑尺寸越大，撞擊坑的裂紋越長，反濺碎片的破裂程度越高。在相同的拉伸強度下，孔隙材料的成坑尺寸明顯小于非孔隙材料對應的成坑尺寸，非孔隙材料撞擊坑邊緣的斷裂程度明顯強于有孔隙材料，其主要原因是孔隙材料沖擊波衰減速度較快，自由面反射的拉伸波較弱，從而材料斷裂程度較輕。

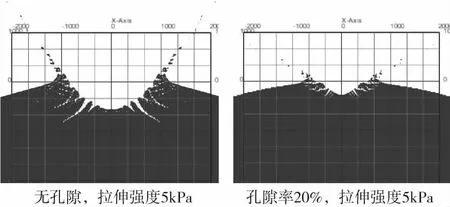
圖4 不同工況下撞擊坑對比

圖5是在典型仿真工況下小行星動能變化曲線。小行星的動能在撞擊后較短時間內達到最大值，隨著沖擊波的傳播緩慢耗散直至保持不變，可以認為此時小行星的動量不再變化。當小行星由孔隙材料組成時，在碰撞過程中小行星獲得的動能峰值要低于非孔隙材料，動能衰減過程也要迅速得多，能夠更快達到穩定狀態，這說明孔隙材料在壓縮過程中對動能的耗散作用顯著，不利于動量傳遞，這與前述撞擊坑形態分析結果相吻合。

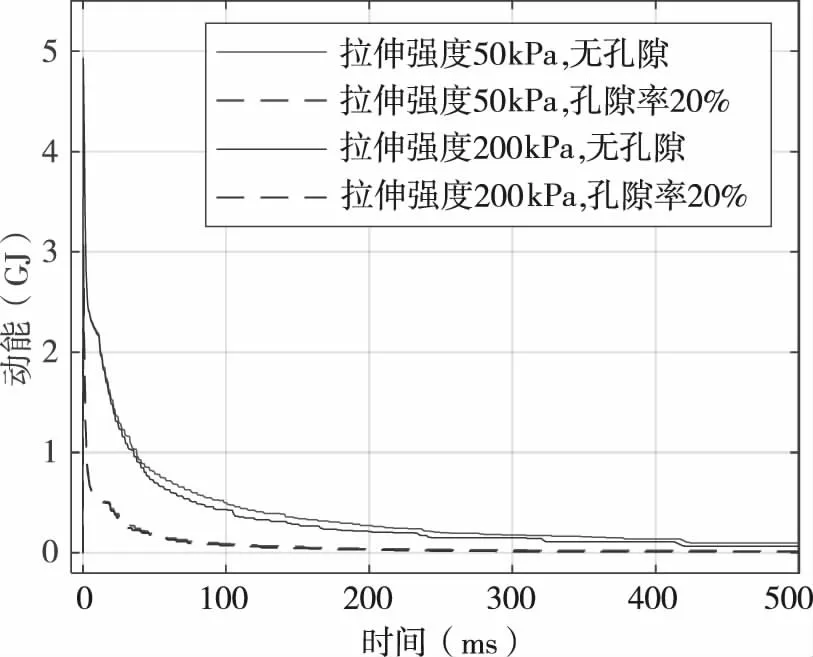
圖5 小行星動能變化曲線

圖6是典型孔隙率下動量傳遞因子與材料拉伸強度關系曲線，拉伸強度越高動量傳遞因子越低。孔隙材料對應的動量傳遞因子明顯低于非孔隙材料。對于非孔隙材料，拉伸強度在200kPa以上時動量傳遞因子基本保持不變，對于孔隙材料，拉伸強度在100kPa以上時動量傳遞因子基本保持不變。動量傳遞因子主要取決于撞擊反濺碎片的質量和速度，而材料拉伸強度越低則產生的反濺碎片越多，速度越高，小行星獲得的動量越大。對于孔隙材料，在孔隙壓縮過程中消耗了較多的動能，導致沖擊波強度快速衰減，在邊界反射回來的稀疏波較弱，從而導致發生斷裂的材料更少，反濺碎片更少，小行星獲得的動量越小。

圖7是典型材料拉伸強度下動量傳遞因子與孔隙率關系曲線。當孔隙率范圍在0%～10%的范圍內時，隨孔隙率的增加，動量傳遞因子迅速下降。當孔隙率大于10%時，隨著孔隙率的增加，動量傳遞因子值基本保持不變。

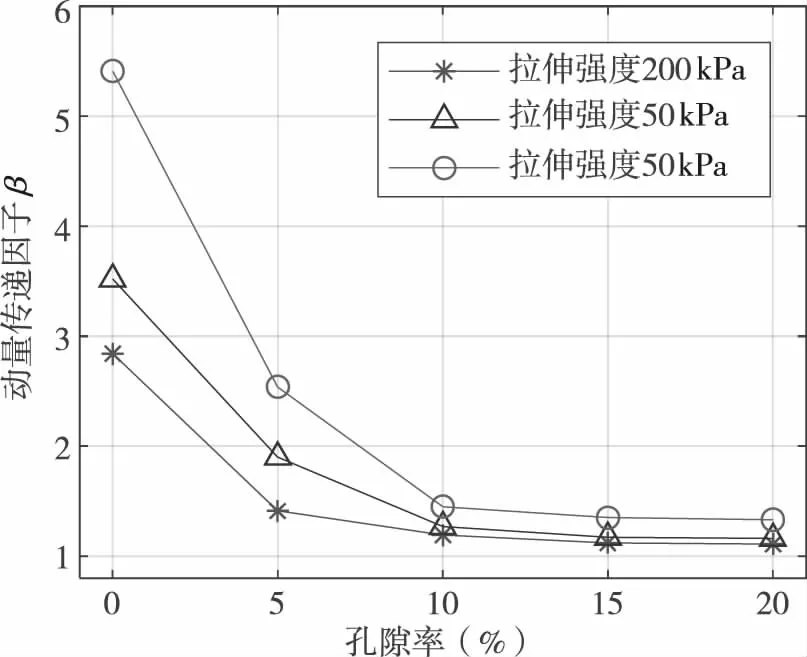
圖7 動量傳遞因子與孔隙率關系曲線

5 結論與展望

基于NASA的DART試驗計劃，開展了動能撞擊偏轉小行星數值仿真，分析了材料拉伸強度和孔隙率對動量傳遞效率的影響規律，結果表明：

(1)采用軸對稱歐拉方法開展動量傳遞效率數值仿真，仿真獲得的動量傳遞因子與試驗獲得的動量傳遞因子較為接近，符合動量傳遞因子隨速度變化規律；

(2)在動能撞擊小行星偏轉仿真中，材料拉伸強度越低，撞擊過程產生的反濺碎片越多，撞擊坑越大，小行星獲得的動量增量越多，動量傳遞因子越高；

(3)在動能撞擊小行星偏轉仿真中，材料孔隙率越高，沖擊波在傳播過程中能量耗散越多，小行星獲得的動量增量越少，動量傳遞因子越低。

小行星撞擊動能偏轉效率還與撞擊點位置、速度、小行星結構形狀等因素相關，本文僅考慮了球形小行星，且只考慮了微觀孔隙。實際上一些石質小行星大多為非均質松散結構，存在宏觀的孔隙和裂紋，因此在下一步工作中將針對宏觀松散結構的小行星，開展動能撞擊偏轉數值仿真，研究動量傳遞效率的其它影響因素。