平面假設在彈塑性變形中的合理應用*

□ 來 勇 □ 李雨林 □ 李智慧

寶雞文理學院 機械工程學院 陜西寶雞 721016

1 研究背景

材料力學理論是建立在試驗認識基礎上的,通過對大量試驗現象的觀察,提出了桿件變形的平面假設,依此假設,推導出桿件軸向拉壓時的應力均勻分布,圓軸扭轉時的切應力沿徑向斜直線分布,梁純彎曲時的應力距中性軸斜直線分布。彈性力學用逆解法將材料力學解代入基本方程,驗證了平面假設嚴格成立。到了塑性力學中,仍由觀察認為小塑性變形條件下,桿件平面假設依然成立,并以此推導了軸、梁在彈塑性變形下的應力場分布形式。平面假設如此重要,它的自然本質是什么？不論材料力學試驗現象觀察,還是彈性力學逆解法,都沒有把問題講清楚。塑性力學仍用簡單觀察來解釋,更使人產生疑問。桿件在力作用下出現變形,是一個自然現象,必有其自然規律,各種不同的變形形式和應力分布必然遵守著一定的自然原理。從能量原理分析入手,可認識到彈性變形這一自然現象存在最小變形能極值原理,金屬材料彈性變形由材料受力原子間距改變而形成,對應的彈性場具有保守場性質,彈性物內的物理量一一對應,且能量守恒。桿件發生的彈性變形,桿件上應力應變分布規則與平面假設都遵循著彈性保守場的性質。塑性變形不具有保守場性質,構件在彈塑性變形時,平面假設不再成立。

2 彈性變形能極值原理

對受力桿件,外力在位移上所做的功等于對應應力在相應的應變上所做的功,可表示為:

(1)

式中:v為體積;s為面積;f為作用在彈性體上的力;p為作用在研究對象表面上的力;σ為與外力所對應的應力;u為位移;ε為位移所對應的應變。

式(1)即為彈性變形虛功原理,也等價于最小變形能原理,即在滿足變形連續條件和位移邊界條件的所有可能變形中,真實的變形使結構變形能為最小值。

由熱力學第二定律,物體受外部影響、從一個平衡態經過一串緩慢變化的平衡態,到達一個新的平衡態,穩定平衡條件下內能是正定的、并取最小值。對工程結構,靜載作用下的彈性變形、彈塑性變形平衡狀態,結構中的內能就是材料中的變形能。因此,受力結構彈塑性靜力平衡時,變形能取最小值是結構變形自然原理或變形規則。

3 桿件彈性變形規則

3.1 圓軸扭轉時變形規則

處在彈性變形階段的受扭圓軸如圖1所示。

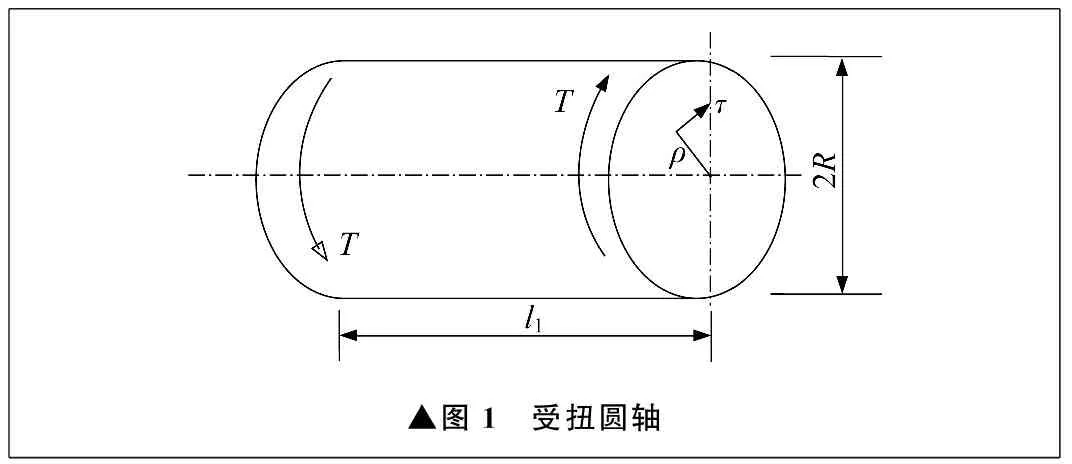
▲圖1 受扭圓軸

圓軸所受扭矩T為:

(2)

總變形能U1為:

(3)

式中:τ為橫截面上任意一點處的切應力;G為材料的切變模量;γ為橫截面上任意一點處的切應變;R為圓軸半徑;ρ為橫截面上所求應力點到圓心的距離;l1為圓軸長度。

若f(x)和g(x)為任意函數,由施瓦茲積分不等式有:

(4)

可在式(4)中令x=ρ,f(x)=ρ1/2γ,g(x)=ρ3/2,則有:

(5)

可得:

(6)

式中:IP為橫截面對圓心的極慣性矩。

式(6)中,僅當γ/ρ為常數時等號成立。由最小變形能原理確定,圓軸彈性扭轉時,變形規則是γ/ρ為常數,應變γ沿徑向線性分布,對應的變形是橫截面作剛性平面轉動。

3.2 純彎曲梁變形規則

處在彈性變形階段的純彎曲梁,如圖2所示。

▲圖2 純彎曲梁

彎矩Mz為:

(7)

總變形能U2為:

(8)

式中:σM為橫截面上任意一點處的正應力;E為材料的彈性模量;εM為橫截面上任意一點處的正應變;y為梁橫截面上任意一點到Z軸的距離;b(y)為距Z軸y處的橫截面寬度;h為梁橫截面的高度;l2為純彎梁的長度。

f(x)和g(x)均為任意函數,可在式(4)中令x=y,f(x)=(b(y))1/2εM,g(x)=(b(y))1/2y,則有:

(9)

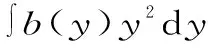
(10)

式(9)中,僅當εM/y為常數時等號成立。由最小變形能原理確定,純彎曲梁彈性變形時,變形規則是εM/y為常數,應變εM距中性軸線性分布,變形是橫截面繞中性軸作平面轉動。

以上分析表明,最小變形能原理確定了桿件彈性變形能及相應的應力和應變的分布規則,即扭轉軸、彎曲梁彈性變形時,其任意一個橫截面均保持為平面,平面假設真實成立。

4 平面假設在塑性力學應用中存在的問題

對于桿件彈塑性小變形問題的求解,過去的研究中也認為平面假設仍然成立。由此推導出,圓軸彈塑性扭轉時,彈塑性切應變沿徑向線性分布,切應力分為彈性區和塑性區,分別呈線性和非線性分布,使用理想彈塑性模型時,應力在橫截面上分布如圖3所示。梁彈塑性純彎曲時,彈塑性線應變距中性軸線性分布,使用理想彈塑性模型時,應力在橫截面上分布如圖4所示。這些理論解已被廣泛應用,但是否準確,應取決于桿件在彈塑性小變形下平面假設是否真實存在。

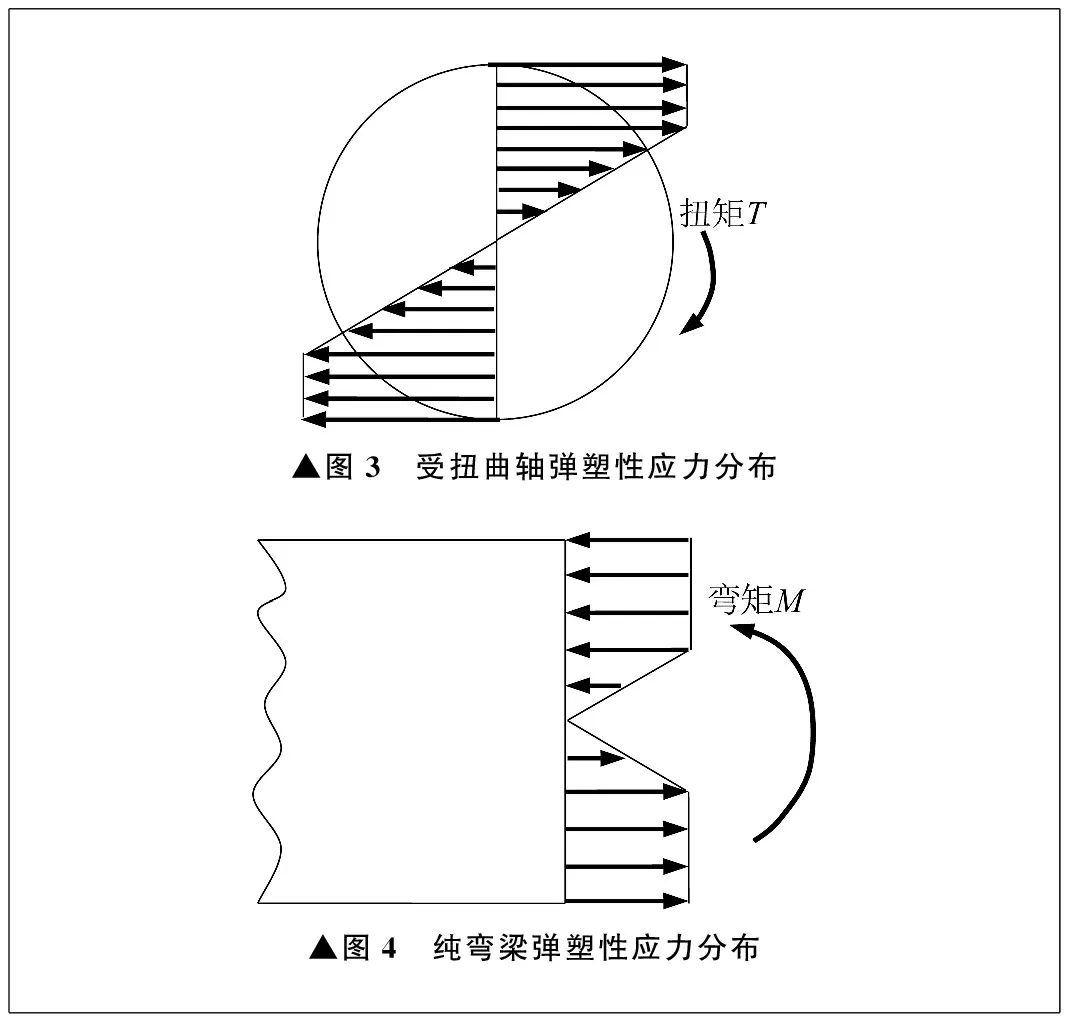
▲圖3 受扭曲軸彈塑性應力分布▲圖4 純彎梁彈塑性應力分布

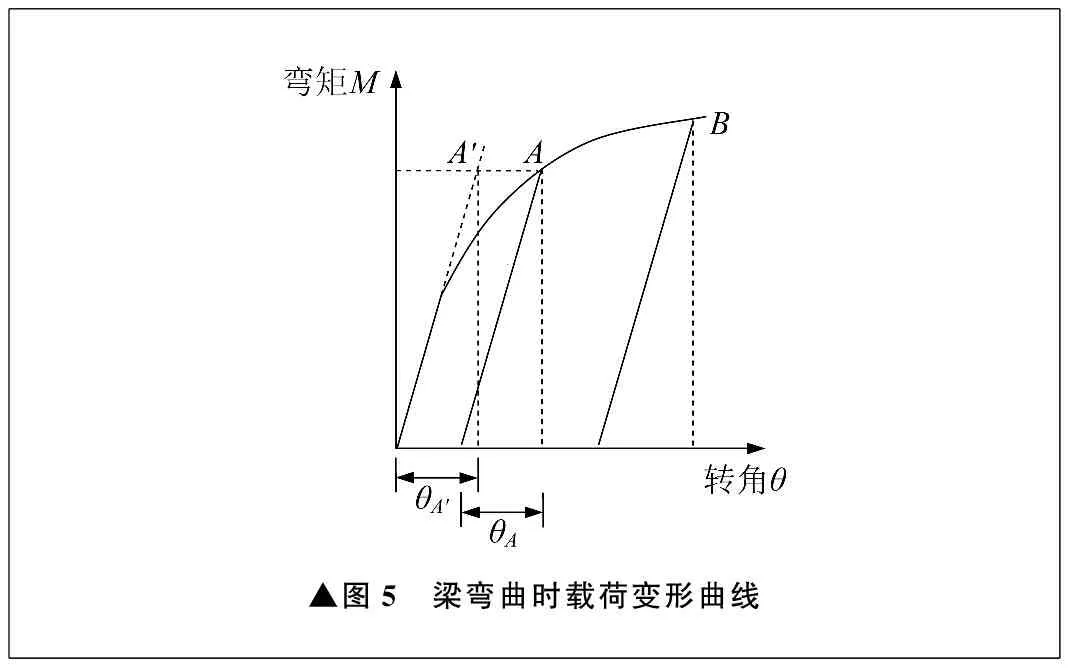
▲圖5 梁彎曲時載荷變形曲線

在彈性變形中,各物理量存在著一一對應關系,所對應的彈性變形規律與應力分布規律也就完全確定。彈塑性變形時,梁中彈性變形仍繞中性軸作平面轉動,平面假設僅在彈塑性變形中的彈性變形部分成立,考慮梁上還有塑性變形發生,那么梁的彈塑性總變形不再符合平面假設。

在彈塑性小變形時,由于塑性變形為永久變形,使桿件幾何形狀發生改變。在考慮塑性變形的桿件新幾何形狀上,桿件內彈性變形仍要滿足變形協調條件,平面假設應是桿、軸、梁等的變形協調條件。

5 結束語

金屬材料彈性變形的主要特征是力、變形、應力、應變,以及變形能一一對應,具有保守場的性質。在彈塑性小變形時,彈性變形性質不發生變化,桿件的受力變形和平面假設由彈性變形性質而決定。彈塑性小變形時,其中的彈性變形仍符合平面假設,而彈塑性總變形則不符合平面假設。