基于BEMD和QWT的遙感圖像去噪算法
閆 昊, 成麗波
(長春理工大學 數學與統計學院, 長春 130022)
0 引 言
遙感圖像去噪是計算機圖像處理領域的關鍵問題。圖像在傳輸的過程中會受到外界因素的影響,從而影響識別。傳統的小波變換可以對遙感圖像去噪,其空間域和變換域在遙感圖像處理中起著至關重要的作用[1-2]。
1998年,Huang等[3]運用經驗模式分解算法(empirical mode decomposition, EMD)進行圖像去噪。2003年,法國學者Nunes[4]將EMD擴展為二維經驗模式分解算法(bidimensional empirical mode decomposition, BEMD),該方法可以應用于圖像壓縮、圖像融合、圖像去噪等方面。2007年,周欣等[5]運用BEMD進行圖像去噪,通過BEMD將被污染的圖像進行分解,得到一系列細節信息和殘余分量信息,并通過實驗驗證了該方法能有效去除高斯白噪聲和乘性噪聲。2009年,何培培[6]利用基于BEMD的圖像去噪算法進行了圖像去噪。
隨著對BEMD研究的不斷深入,其理論逐漸趨于成熟,研究者們不斷改進BEMD方法處理遙感圖像。2013年,易三莉等[7]設計了BEMD與自適應維納濾波的圖像去噪算法,該方法將圖像分解為不同頻率的子圖像,分別對每一個子圖像去噪。2014年,賀一楠等[8]運用二維經驗模式分解方法進行遙感圖像去模糊處理。2021年,侯欣雨等[9]提出BEMD二次分解,并與維納濾波相結合,該方法可以對彩色圖形進行去噪處理。
2006年,Corrochano[10]提出了四元數小波變換理論(quaternion wavelet transform, QWT),并用四元數相位的概念推導出四元數小波金字塔。2010年,喬麗紅[11]把四元數解析方法運用到提取二維本征模態函數(intrinsic mode function, IMF)的譜特征中,并運用四元數解析方法得到二維解析信號。2012年,Yin等[12]提出四元數小波變換方法,得到去噪圖像。同年,殷明等[13]建立了一種基于四元數小波變換的隱馬爾可夫樹模型,該模型對圖像噪聲的去除有顯著效果。2013年,陳北京等[14]對四元數去除泊松噪聲的加權平均濾波器進行深入研究,對彩色圖像進行整體處理。2015年,王亞萍[15]詳細地介紹了小波變換和雙樹四元數小波變換理論,并對雙樹四元數小波變換理論進一步完善,從而達到了圖像增強的目的。2017年,Fletcher等[16]對四元數小波變換的內容作了進一步闡述。
本文根據遙感圖像信息及噪聲分布特征,設計了一種BEMD與四元數小波變換遙感圖像去噪算法,通過實驗驗證該方法具有可行性。
1 二維經驗模式分解
EMD方法起初是由Huang等提出,可以處理非線性、非平穩性信號。與傳統方法相比,該方法具有顯著的優越性。而BEMD是EMD方法的一個推廣,它可以將圖像f(x,y)分解成若干細節信息和趨勢信息,其表達式為
(1)
式中:IMFi表示圖像的細節信息,i值越小表示越早分離出來IMF;余項函數r(x,y)表示了圖像的結構框架。
2 本文算法實現
四元數域可由實小波和復小波變換推廣得到,四元數小波變換相位信息豐富,時頻局部化能力較強,它的尺度函數及水平、垂直、對角方向的小波函數的具體形式如下:
(2)
由公式(2)可知,四元數小波變換分為4個實小波,第1個離散的實小波與四元數小波的實部相對應,其余的每個分量分別經過了部分或全部的Hilbert變換。
本文結合BEMD和四元數小波變換算法進行遙感圖像去噪,其具體算法如下:
Step 1 將含噪圖像進行BEMD分解,得到5個IMF分量和1個殘余分量;
Step 2 將第1個IMF分量進行四元數小波變換并對其進行硬閾值去噪,得到的圖像進行四元數小波逆變換,最后得到最終的IMF分量;
Step 3 對遙感圖像各分量進行重構得到去噪后圖像。
3 實例分析
3.1 實驗條件
實驗采用256×256像素的資源三號多光譜樣例圖像和高分七號多光譜樣例圖像作為實驗分析對象進行去噪分析,分別添加方差為10,15,20的高斯噪聲。
含噪的圖像經過BEMD分解得到5個IMF分量和1個殘余分量。由于噪聲主要存在于第1個IMF分量中,因而需要選取第1個IMF分量;然后對第1個IMF分量進行四元數小波變換并進行硬閾值去噪,再通過四元數小波逆變換得到去噪后的IMF分量;最后通過BEMD逆變換得到去噪后圖像,如圖1和圖2所示。可以看出,該方法能去除含噪遙感圖像的噪聲,可以突出遙感圖像的細節信息。

(a) σ=10(b) σ=15(c) σ=20

(a) σ=10(b) σ=15(c) σ=20
遙感圖像去噪質量隨著圖像方差的增大而降低,這一點從均方誤差、峰值信噪比結構相似度可以看出(表1和表2)。

表1 不同方差下資源三號多光譜樣例圖像去噪質量評價表

表2 不同方差下高分七號多光譜樣例圖像去噪質量評價表
由圖1和圖2可知,圖像的去噪效果與噪聲方差的大小有關,隨著方差增大,圖像的去噪效果變差,從視覺上看,圖像逐漸變得不清晰。由表1和表2可知,圖像的均方誤差隨方差增大而增大,而峰值信噪比和結構相似度隨方差增大而減小,實驗表明該方法對方差較小的含噪圖像去噪效果較好。
3.2 對比實驗
本文采用BEMD和四元數小波變換算法完成遙感圖像去噪過程并進行了深入分析,與小波算法、BEMD相比,該方法有效可行。
實驗采用資源三號多光譜樣例圖像和高分七號多光譜樣例圖像作為實驗分析對象,但由于條件有限,人為添加了方差為10的高斯噪聲,從而得到2幅加噪后的遙感圖像。對這2幅圖像分別采用BEMD和四元數小波變換算法、小波算法、BEMD進行遙感圖像去噪,主觀評價如圖3和圖4所示,客觀評價見表3和表4。

(a) 小波去噪(b) 二維經驗模式分解(c) 本文方法
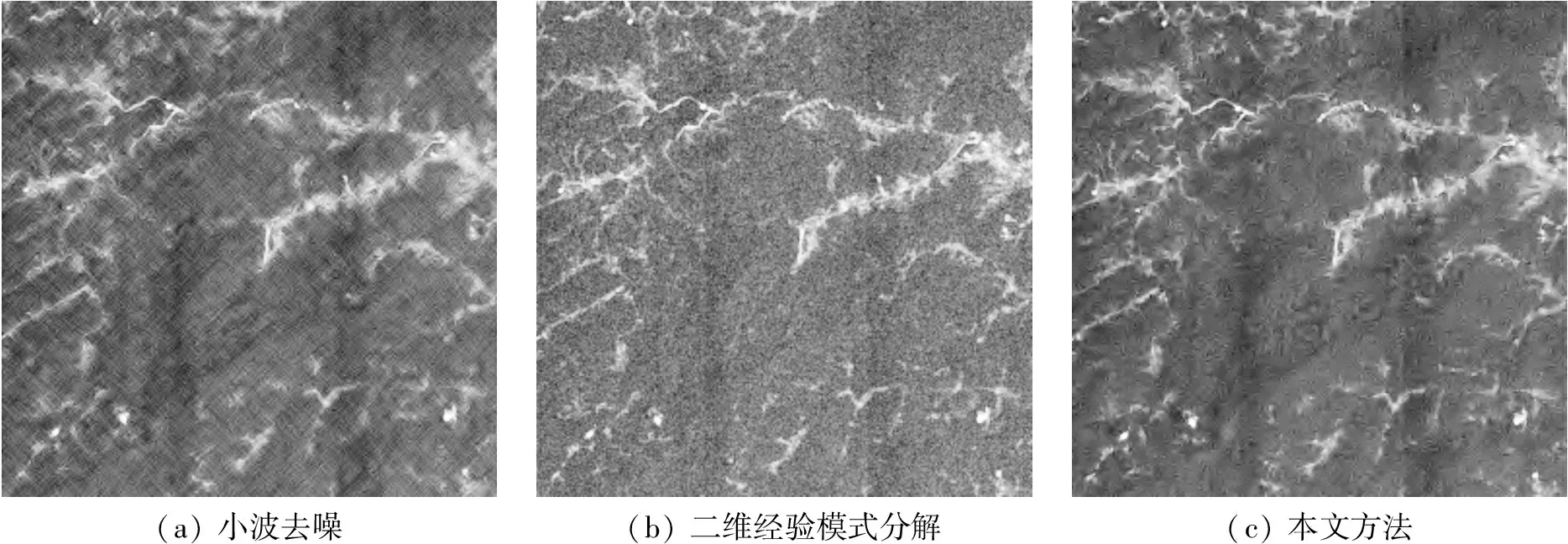
(a) 小波去噪(b) 二維經驗模式分解(c) 本文方法

表3 資源三號多光譜樣例圖像去噪質量評價表

表4 高分七號多光譜樣例圖像去噪質量評價表
由圖3和圖4可知,本文方法可以保留遙感圖像的細節信息,從視覺上看,該方法具有明顯的去噪效果。由表3和表4可知,本文方法可以使圖像有較高的峰值信噪比和結構相似度,降低了均方誤差,這表明該方法可以彌補傳統去噪方法的不足之處,使去噪效果得以提升。
4 結 語
本文將BEMD與四元數小波變換結合進行遙感圖像去噪。實驗結果表明,本文算法去噪能力優于傳統算法,能有效降低圖像的均方誤差,提高峰值信噪比和結構相似度,從而達到去噪的目的。通過對比實驗可以證明該方法確實有效可行,但去噪后的圖像仍然不夠清晰,圖像信息或多或少存在失真的現象。

