基于平衡附加力原理的微動放大機構設計與實驗

楊滿芝 李林岳 張傳偉 魏凱洋 黨 蒙 景 鋼

(西安科技大學機械工程學院， 西安 710054)

0 引言

隨著現代科學技術的不斷發展，精密、超精密加工技術成為機械加工非常重要的方向，對精密運動進行研究具有重要意義[1-5]。在精密運動中，微動機構既能作為微動系統的執行單元輸出精密位移，又能作為宏微驅動系統補償機構實現大型高精度運動[6-9]。目前微動系統大多使用壓電陶瓷致動器(Piezoelectric ceramics，PZT)、超磁致伸縮器(Giant magnetostrictive actuator, GMT)等驅動器直接進行驅動，但這些微驅動器的輸出位移較小，難以實現較大的微位移運動，從而導致宏微驅動補償范圍較小。為了突破微動機構運動范圍的限制，需要對微動放大機構設計及性能進行研究。

為了實現微動機構的放大功能，許多學者對微動放大機構進行了研究。李佳杰等[10]設計了一種利用杠桿原理進行放大的二級差動微位移放大機構，采用應用矩陣表示法對其進行運動靜力學分析與優化。SU等[11]設計了一種用于微機電系統的機械放大器，介紹了單級杠桿和多級杠桿在內的設計和綜合理論，可根據需求來給出最佳杠桿級數。KEE-BONG等[12]提出了一種新穎的壓電驅動柔性平臺，該平臺引入了兩個平行布置的機械放大機構，其輸出位移及輸出力均得到增大。LING等[13]提出了一種菱形和橋型柔順機構位移放大率的增強理論模型，并完成了模型建立和有限元分析，得出將橋式彎曲簡化為菱形結構進行力學建模位移放大率誤差會增大。BOLZMACHER等[14]設計了一種新型微機械放大單元，用于將壓電微驅動器的行程增加到高頻，以便于在相對較高的工作頻率下表現出相對較大的沖程。NICOLAE等[15]基于應變能和Castigliano位移定理解析出封閉形式的方程，制定了一種用于計算具有單軸彎曲鉸鏈的平面柔順機構的位移和剛度的解析方法。KIM等[16]設計了一種雙平行四邊形的放大機構，可利用傾斜結構來實現位移放大。

微動機構在運動方向上運動精度要求較高，且微致動器在運動方向一般可承受較大應力，而非運動方向一般較為脆弱[17-25]，如果在工作狀態中產生附加位移及附加力，非運動方向附加位移會導致運動不精密，非運動附加力則會對微致動器安全造成嚴重影響，而以上研究未考慮附加位移及力對微動機構影響。本文設計一種無附加力及附加位移的精密微動放大機構，并對機構強度、動態、運動學進行分析。

1 精密微動放大機構設計

1.1 平衡附加力原理

微動機構的放大功能一般采用如圖1所示的杠桿原理工作，右端點q與底座連接，為固定端；s處為位移輸入端；t處為位移輸出端。在壓電陶瓷的輸入位移Δu的作用下，輸入端沿y方向運動，此時端點q固定，輸入位移被放大，在輸出端沿y方向運動，將輸入位移Δu放大為輸出位移Δv。

圖1 杠桿原理示意圖Fig.1 Schematics of lever principle

微動機構的平衡附加力原理如圖2所示，將微驅動器在矩形槽E內連接固定，機構對稱設計有8個柔性鉸鏈組件(柔性鉸鏈1～16)。當驅動器產生驅動位移時，柔性鉸鏈會發生形變，除產生主運動方向的力外還會產生非運動方向的力，此時對稱分布的8個柔性鉸鏈組件由于形變產生的非運動方向的力大小相等、方向相反，可以互相平衡，實現了柔性鉸鏈的附加力及附加位移平衡。平衡附加力原理避免了微動機構產生非運動方向的位移，同時保護了驅動器免受水平方向力的破壞，確保了微動系統的精密性和安全性。

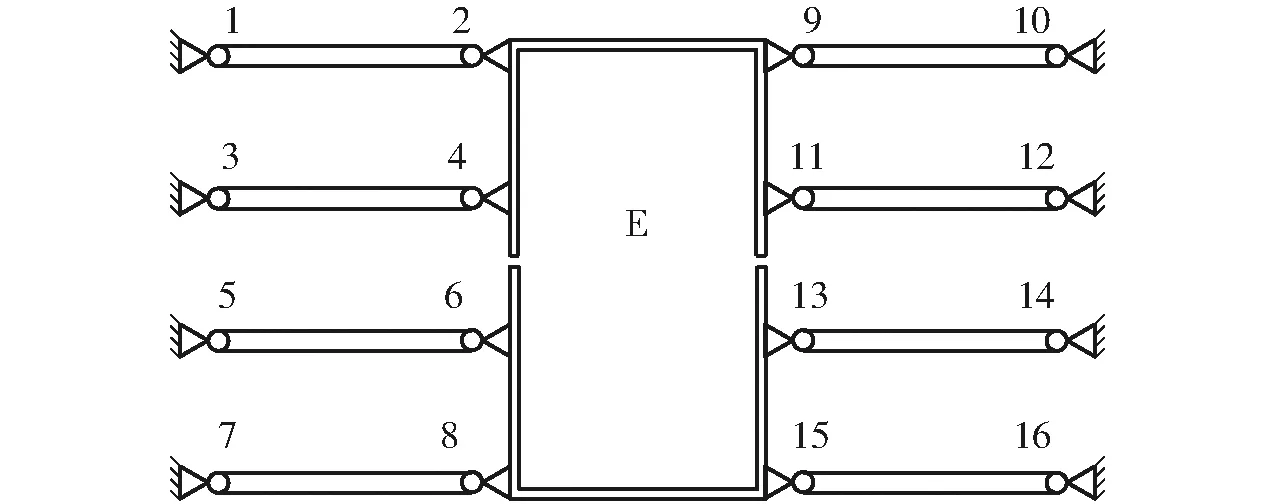
圖2 柔性鉸鏈平衡附加力原理示意圖Fig.2 Schematic of principle of additional force balance of flexible hinge

1.2 精密微動放大機構設計

根據杠桿原理結合平衡附加力原理，本文設計了一種可將運動輸入精密放大的微動機構，設計放大比1∶1.5，結構示意圖如圖3所示。微動放大機構的外形尺寸為150 mm×157 mm×50 mm。機構包含24個相同的直圓型柔性鉸鏈，每個柔性鉸鏈的半徑長度和最小距離分別為3 mm和1 mm(圖3的局部放大圖)。將機構b部分固定在工作臺上，在微驅動器的驅動作用下輸入機構a部分獲得y軸正向輸入位移Δu，根據杠桿原理微動放大機構對輸入位移進行y軸精密放大，從輸出機構c部分獲得輸出位移Δv。在機構工作過程中，兩側對稱分布的柔性鉸鏈13～24根據平衡附加力原理，非運動方向上的力和位移會進行抵消，使得機構在工作時無附加位移及附加力產生，從而保證機構良好的精密性和安全性。

圖3 微動放大機構結構示意圖Fig.3 Schematic of structure of micro-drive amplifying mechanism

由于柔性鉸鏈是通過自身薄弱部位材料產生的可逆彈性形變來傳遞運動，所以對材料的選取有較為嚴格的要求。選用60Si2Mn、65Mn、QBe2作為微動機構材料，其參數如表1所示。

表1 3種柔性鉸鏈材料參數Tab.1 Three material parameters of flexible hinge

1.3 放大比計算

設計微動機構時，可對機構結構進行調整以便獲得需要的放大比。以放大比1∶1.5為例，其他場景可根據調整機構結構以獲得所需要的放大比。微動機構兩側呈對稱分布，在分析時只需對微動放大機構的單側進行分析。

在微動機構運動過程中，各柔性鉸鏈會產生變形從而使得其回轉中心產生偏移，設柔性鉸鏈i(i=1，2，…，24)受到的軸向力為Fi，力矩為Mi，鉸鏈產生的軸向變形量為Δi，轉動角為αi，則有

Fi=KFΔi

(1)

Mi=KMαi

(2)

(3)

(4)

式中KF——軸向拉壓剛度

KM——轉角剛度

E——彈性模量

s——鉸鏈半徑與最小厚度之比

在杠桿放大機構中，柔性鉸鏈轉角α2和桿件轉角θ1之間存在關系

α2=θ1

(5)

微動放大機構受力分析如圖4所示。由1.1節微動放大機構工作原理可知，微動放大機構理論放大倍數為

(6)

式中A——微動機構放大比

Y6——柔性鉸鏈6位移

Y3——柔性鉸鏈3位移

l1——杠桿機構的輸入端到固定端長度

l2——杠桿機構輸出端到固定端長度

圖4 放大比幾何計算模型Fig.4 Amplification ratio geometric calculation model

將所設計的微動放大機構的參數代入式(6)計算可得微動放大機構放大比A為1.5。

2 強度

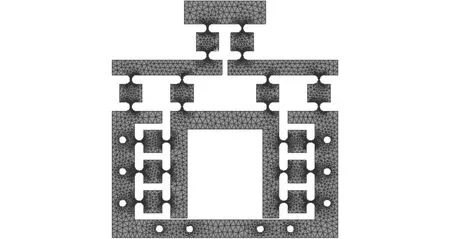
圖5 微動放大機構網格劃分圖Fig.5 Grid division diagram of micro-drive magnifying mechanism

利用有限元軟件對微動放大機構模型進行網格劃分，如圖5所示，模型共劃分為366 048個單元，544 272個節點。將微動放大機構上邊緣10個螺栓孔圓柱面固定，對機構中驅動器的位置處施加Y軸正向位移15 μm，分析得到微動放大機構應力如圖6所示，由圖6可知最大模擬應力為41.928 MPa。

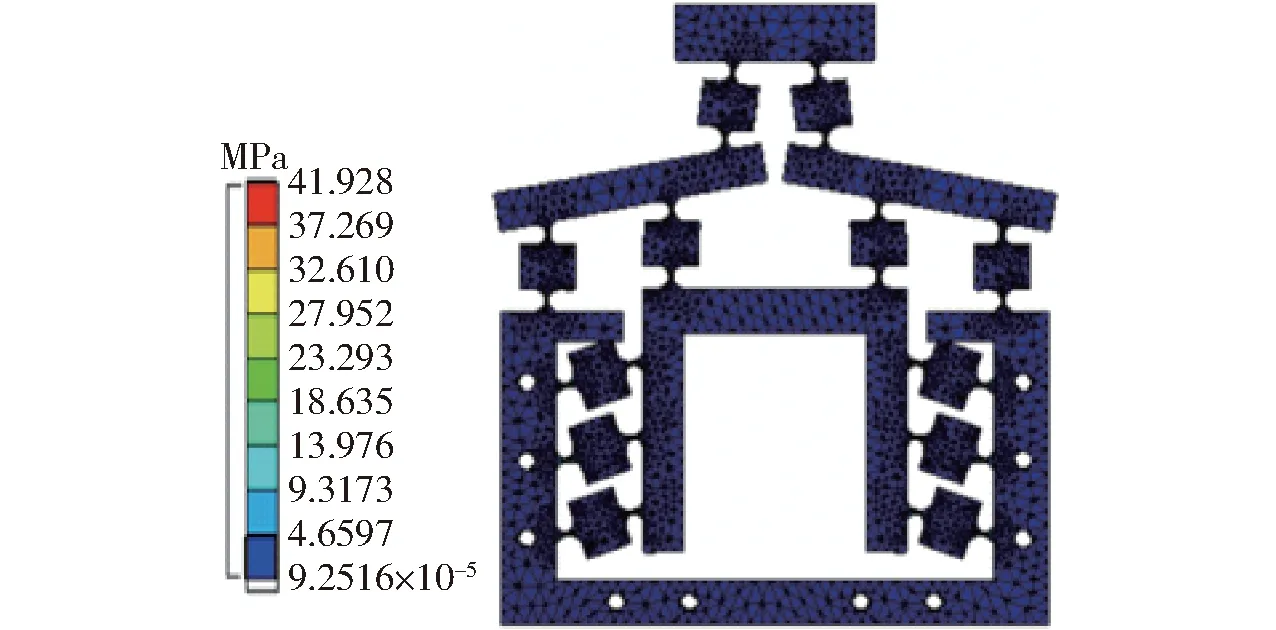
圖6 微動放大機構應力云圖Fig.6 Stress cloud diagram of micro-drive magnifying mechanism

材料許用應力計算式為

(7)

式中 [σ]——材料許用應力

σs——材料屈服極限

λ——安全系數，取1.5

根據式(7)可求得材料的許用應力[σ]為784 MPa，而微動放大機構的最大模擬應力僅為41.928 MPa，遠小于材料的許用應力。因此，微動放大機構具有較好的強度性能，且能夠滿足設計要求。

3 動態性能

3.1 有限元分析

采用有限元法的動力學模塊對微動放大機構進行自由模態分析，其前6階固有頻率為529.8、579.11、805.32、964.11、1 198.9、1 304.2 Hz。

3.2 動態性能實驗

實驗采用德國M+P動態測試控制分析系統、數據采集前端、高精度力錘、橡皮繩、微動放大機構及計算機等實驗儀器與設備，進行微動放大機構自由動態實驗，實驗裝置如圖7所示。將微動機構用橡皮繩懸掛，數據采集前端固定在機構上，另一端與M+P動態測試控制分析系統相連接，使用高精度力錘敲擊自由懸掛的微動機構可以測得其固有頻率，微動機構前6階固有頻率實驗結果如圖8所示。

圖7 微動放大機構動態性能實驗裝置Fig.7 Experimental device of dynamic performance of micro-drive amplifying mechanism1.微動放大機構 2.數據采集儀前端 3.高精度力錘 4.M+P動態測試控制分析系統 5.計算機

圖8 微動放大機構前6階固有頻率實驗結果Fig.8 Experimental results of the first six order natural frequencies of micro-drive amplification mechanism

通過有限元及實驗分析，微動放大機構的前6階固有頻率結果對比如表 2 所示。由表 2可知，有限元及實驗分析結果較為一致，其最大相對誤差為9.41%，分析結果準確可信。且其最低固有頻率為530 Hz左右，而本文選用P235.1s 型壓電陶瓷致動器最大驅動頻率為300 Hz，因此微動機構在運動過程中不會發生共振現象。因此，微動放大機構動態性能優良，且運動過程中不會發生低頻共振現象，符合設計要求。

表2 機構固有頻率有限元與實驗分析對比Tab.2 Comparison between finite element method and experimental analysis of mechanism’s natural frequency

4 運動學分析

4.1 有限元分析

為了方便研究，對微動放大機構在輸入位移0～7 μm范圍內的運動性能進行測試，利用印記方法對微動機構施加輸入位移0.50 μm，如圖9所示，采用probe(探針功能)計算機構輸出位移。

圖9 微動放大機構的有限元分析Fig.9 Finite element analysis of micro-drive amplifying mechanism

4.2 運動學實驗

實驗采用德國PI公司P235.1s型壓電陶瓷致動器(其參數見表3)、電感式傳感器(1號傳感器為旁式傳感器，其分辨率為0.03 μm；2號傳感器為直式傳感器，其分辨率為0.05 μm)、微動放大機構、實驗底座、MDG-8型數據采集儀等實驗儀器與設備，微動放大機構運動實驗如圖10所示。實驗利用1號傳感器(旁式傳感器)測量微動機構的輸入位移，利用2號傳感器(直式傳感器)測量微動機構的輸出位移，利用壓電陶瓷致動器輸入不同位移可以獲得不同的輸出值，實驗結果如表4所示。

表3 P235.1s型壓電陶瓷致動器主要技術參數Tab.3 Main technical parameters of P235.1s piezoelectric ceramic actuator

圖10 微動放大機構實驗實物Fig.10 Experimental object of micro-drive amplifying system1.1號傳感器 2.PZT 3.2號傳感器 4.微動放大機構 5.實驗底座

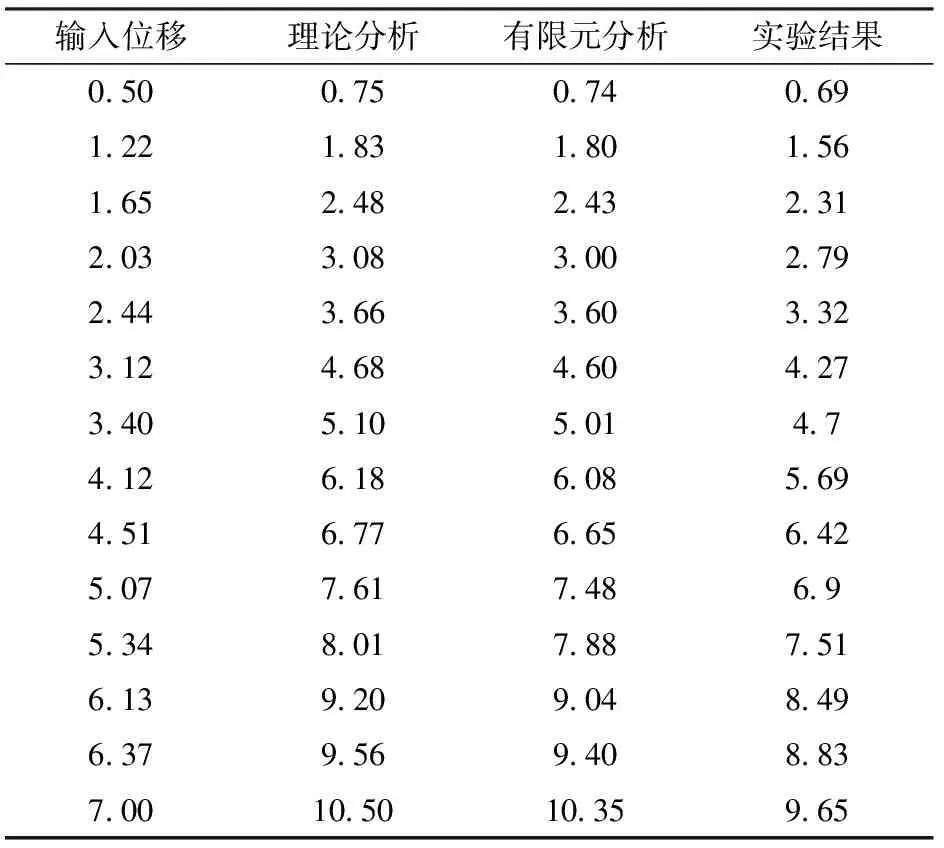
表4 微動放大機構運動學分析3種方法實驗結果Tab.4 Comparison of three methods for kinematic analysis of micro-drive amplification mechanism μm

4.3 對比分析

通過式(6)可計算出各個輸入位移對應輸出的理論分析值，理論分析、有限元分析和實驗結果對比如表4所示，對三者分析進行結果擬合如圖11所示。

圖11 微動放大機構運動學分析Fig.11 Kinematics analysis of micro-drive amplifying mechanism

對理論分析進行擬合，得到線性方程式為

Δv=1.5Δu(R=1)

(8)

對有限元分析進行擬合，得到線性方程式為

Δv=1.48Δu(R=1)

(9)

對實驗結果進行擬合，得到線性方程式為

Δv=1.39Δu-0.04 (R=0.998)

(10)

結果表明微動系統的輸入位移與輸出位移具有運動精度及線性度較高的優點。利用擬合的線性方程(8)～(10)斜率的計算理論分析值與實驗值的相對誤差為9.4%(二者最大絕對誤差為0.85 μm)，有限元分析值與實驗值相對誤差為7.8%(二者最大絕對誤差為0.57 μm)。同時，運動線性擬合相關系數不小于0.998。

為了方便工程應用，根據式(8)～(10)可將微動放大機構的運動輸入與輸出關系擬合為

Δv=1.456Δu

(11)

誤差產生的原因包括機構加工誤差、有限元模型導入誤差、實驗室檢測環境誤差等，可通過提高加工精度、細化有限元網格、降低實驗室振動、噪聲等外界干擾等方法降低誤差。運動學實驗過程中壓電陶瓷致動器安全運行，也可證明本文設計的微動機構無附加力存在。

5 結論

(1)設計的一種精密放大機構，系統的放大比可根據需求調節，可將直線位移按照需要放大，以滿足不同的大行程高精度應用場合。

(2)設計的微動放大機構根據平衡附加力原理，在工作時不會產生非運動方向力及位移，能夠有效保證其運動的安全性及精密性。

(3)采用有限元法完成系統強度分析、有限元法及實驗完成動態性能分析，分析結果表明系統強度性能滿足設計及使用需求，且系統動態性能良好(一階固有頻率為580 Hz、固有頻率分析有限元及實驗最大相對誤差為9.41%)、運動過程中不會發生共振。

(4)通過理論分析、有限元及實驗完成機構運動學分析，結果表明系統運動精度及性能線性度高，并給出了其運動性能擬合方程。運動學分析中理論分析值與實驗值相對誤差為9.4%，最大絕對誤差為0.85 μm；有限元分析值與實驗值相對誤差為7.8%，最大絕對誤差為0.57 μm；機構運動線性方程相關系數不小于0.998。