小波閾值降噪提高BOTDR 測量精度研究*

孫志杰，崔 寧，白 清，*，張 軍，王清琳，王 宇，，劉 昕，靳寶全

(1.山西省交通科技研發有限公司公路工程研究院，山西 太原 030006；2.太原理工大學 新型傳感器與智能控制教育部重點實驗室，山西 太原 030024；3.山西省智慧交通研究院有限公司 智慧交通山西省實驗室，山西 太原 030006)

分布式光纖傳感技術可實現溫度、振動、應變等多種物理量監測，具有耐腐蝕、抗電磁干擾及長距離等優勢，近年來受到研究人員廣泛關注[1-2]。其中，基于光纖自發布里淵散射效應的布里淵光時域反射儀(Brillouin Optical Time Domain Reflectometer，BOTDR) 可利用光纖中的布里淵頻移(Brillouin Frequency Shift，BFS)改變量實現溫度或應變測量[3]。該技術僅需單端注入探測光，探測距離長，無需構建光纖環路，易于工程實施與維護，目前已廣泛應用于大型基礎設施的安全監測等領域[4-5]。然而，由于光纖中后向自發布里淵散射強度十分微弱，且工程中傳感光纜多鋪設于野外環境，傳輸損耗大，因此BOTDR 通常存在信噪比較低的缺陷[6]，進而導致系統BFS 測量精度較差。

針對這一問題，國內外研究人員從硬件結構到處理算法提出了一系列優化方案。南京大學張旭蘋教授等[7]提出了一種電光調制器與同步光開關相結合的新型光脈沖調制方案，通過提高探測脈沖消光比，將25 m 空間分辨率下48.5 km 光纖末端BFS測量誤差由5.2 MHz 降低到0.8 MHz，通過64 bit 互補Golay 編碼探測進一步提升了測量精度[8]。中科院上海光機所的蔡海文教授等[9]將Simplex 脈沖編碼與數字相干檢測技術相結合，在1 km 測量距離和4 m 空間分辨率條件下，將BFS 測量誤差由23.18 MHz 降低至9.08 MHz。浙江大學宋牟平教授等[10]將前向拉曼光纖放大與BOTDR 結合，在40 m 空間分辨率下，在100 km 光纖上實現了±3 °C 的測溫精度。諾森比亞大學的Lalam 等[6]將多波長探測與無源消偏裝置相結合，在50km 光纖及5 m空間分辨率條件下上獲得了3.92 dB 的信噪比提升。中國科學技術大學夏海云教授等[11-12]將單光子探測器和高分辨率Fabry-Perot 干涉儀用于BOTDR 系統，進一步提升了系統測量精度。上述硬件優化方案從散射信號強度和系統探測靈敏度進行提升，進而提高了BOTDR 測量精度，但是需添加額外的光電器件來實現，增加了系統成本與控制復雜度。為此，研究人員針對布里淵增益譜擬合算法進行了改進，以實現噪聲抑制。英國劍橋大學的Yu 等人[13]通過蒙特卡羅方法證明了二階多項式擬合可提高BFS 測量精度。中科院上海光機所蔡海文教授等[14]提出了一種迭代擬合方法來進一步提高BFS 測量精度。燕山大學付興虎等[15]提出基于自適應慣性權重調制和粒子群優化算法的BFS 擬合方法，提高了測量精度。華北電力大學李永倩教授等[16]提出了一種面向多峰BGS 的多參數特征提取算法，可改善測量速度和精度。長春理工大學段潔等[17]采用自適應梯度下降算法(Adam 算法)對布里淵散射信號進行擬合計算，進一步提高了擬合測量精度。然而，對于頻率掃描式BOTDR 來說，布里淵增益譜擬合通常需要數十個頻率點下的功率曲線作為輸入數據[18]，每條功率曲線的測量噪聲均會影響系統精度。因此，抑制每條功率曲線的噪聲，為功率譜擬合提供高精度數據源，對于進一步提升BOTDR 測量精度具有重要意義。

綜上所述，本文采用小波閾值降噪算法對掃頻過程中的每條單頻點功率測量曲線進行降噪處理，以提升BOTDR 測量精度。簡述了BOTDR 小波閾值降噪原理，構建了基于微波外差掃頻的BOTDR仿真模型，通過仿真研究確定了小波閾值降噪算法最優參數，最終搭建BOTDR 溫度測量裝置對降噪效果進行了實驗驗證。

1 小波閾值降噪理論研究

1.1 小波閾值降噪原理

對于一個連續信號F(t)而言，可以通過傅里葉變換等效為不同幅值和頻率的三角函數加權和。類似地，連續信號F(t)的小波變換可定義為[19]:

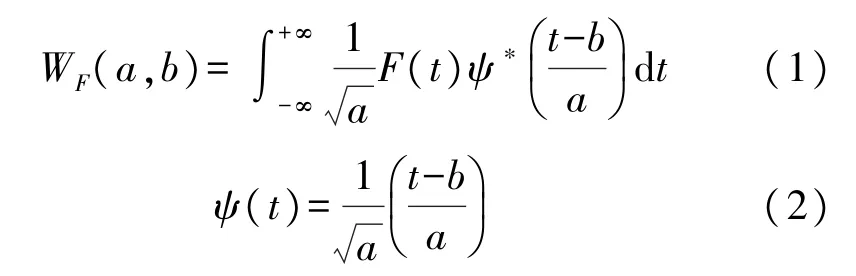
式中:ψ(t)為小波基函數，ψ*(t)為ψ(t)的共軛函數，a為尺度因子，b為平移因子。在實際應用中，與傅里葉級數相類似，一個連續信號F(t)也可以同樣看作不同尺度下小波基的線性組合[20]:

式中:ψj，k(t)由小波基函數平移和伸縮得到，Cj，k為小波變換系數。小波變換對于信號的處理本質就是基于閾值規則選用合適的小波參數和系數對真實信號進行重構逼近，最終達到抑制噪聲的目的。

圖1 為BOTDR 小波閾值降噪原理示意圖。如如圖1(a)所示，FS-BOTDR 系統需通過頻率掃描測量來獲取BFS 分布。首先，隨著掃描頻率點的步進變化，采集不同頻率點下的功率-時序單頻曲線，之后將所有測得的單頻曲線按照頻率-距離進行組合得到三維布里淵增益譜(Brillouin Gain Spectrum，BGS)，最終通過洛倫茲擬合及最大值尋峰后獲得BFS 沿光纖分布曲線。

圖1(a)中所示BOTDR 測得的單頻曲線yi(t)可以表示為:

圖1 BOTDR 小波閾值降噪原理示意圖

式中:si(t)為真實信號，ei(t)為噪聲信號。在實際測量中，單頻功率曲線通常為緩變低頻信號，而噪聲信號大多分布在高頻分量中。如圖1(b)所示，在小波閾值降噪算法中，含噪信號yi(t)經過n次小波變換后，可分解為多組高頻細節信號與一組低頻近似信號。根據信號與噪聲的小波系數數值不同這一特性，通過對高頻系數做閾值處理，最終通過小波重構就可以實現信號與噪聲的分離。如圖1(c)所示，降噪后的多條單頻曲線可以組合為毛刺較少的三維BGS，進而為后續的擬合尋峰提供高質量數據，最終提升BFS 分布的測量精度。

在小波閾值降噪的過程中，涉及的主要參數有:小波基函數及消失矩階數、小波分解層數、閾值規則。常用的小波基函數有dbN、symN、coifN 等，其中N 為消失矩階數。分解層數即小波變換的次數，對于小波閾值降噪，分解層數直接決定了降噪效果與信號的真實還原度。閾值規則對于信號的小波閾值降噪效果也會產生影響。硬閾值處理函數的不連續性會導致處理后信號出現偽吉布斯效應，造成降噪效果下降，因此小波降噪中通常使用軟閾值處理方法。本文將以軟閾值規則minimaxi 為基礎，通過仿真研究較優的小波基函數和小波分解層數，為降噪實驗提供理論支撐。

1.2 小波閾值降噪仿真研究

為優化選擇合適的小波閾值降噪參數，搭建了FS-BOTDR 理論模型進行仿真研究。首先構建單一頻率點下的功率時序曲線原始信號和加噪信號，對每個頻率點下的單頻時序曲線進行降噪，然后將全部頻率點降噪后的時序曲線組合為三維布里淵增益譜，最終通過進一步尋峰擬合獲取BFS 分布。

仿真研究中，首先構造單頻時序曲線。設置傳感光纖長度為10 km，常溫下光纖布里淵頻移為10.7 GHz，溫度改變區為9 km 處，長度約150 m。為便于觀察功率曲線上升部分且考慮到傳感光纖前端可能存在部分傳感盲區，在光纖前端設置約50 m 為無光盲區。此外，為模擬測量過程中的各類隨機噪聲，引入10 dBm 的高斯白噪聲信號，所得的單頻曲線原始信號和加噪信號如圖2 所示。可以明顯看出，加入噪聲后原始信號功率波動增大，設置的變溫區域已經完全被噪聲湮沒，從加噪信號單頻曲線中已幾乎無法識別出功率突變區域。

圖2 單頻點功率時序仿真曲線

在單頻功率曲線基礎上，進一步構建三維BGS。設置室溫區光纖BGS 中心頻率點為10.7 GHz，半高全寬為100 MHz，變溫區布里淵頻移增大為10.76 GHz，用以模擬光纖發生溫度升高。微波源掃頻步進設定為5 MHz，白噪聲強度保持10 dBm，模擬微波掃頻過程可得到如圖3 所示的加噪聲三維BGS 分布。可明顯看出，在加噪三維BGS 分布中，光纖末端變溫區強度變化已幾乎被噪聲信號淹沒，信噪比較差，難以準確識別出溫度升高引起的功率變化。

圖3 加噪三維BGS 仿真結果

為初步驗證小波閾值降噪算法的噪聲抑制效果，針對圖2 中的單頻加噪信號進行降噪處理。在仿真中設置初始降噪方案參數為:minimax 規則軟閾值處理，symN 小波基，分解層數為4。小波閾值降噪處理結果如圖4 所示。可以看出，降噪后的單頻功率曲線波動顯著減小，變溫區信號已經可以較清晰還原。在后續仿真研究中，通過改變分解層數、小波基函數及消失矩階數，對比不同參數下的降噪效果，從而實現小波閾值降噪算法參數優化。

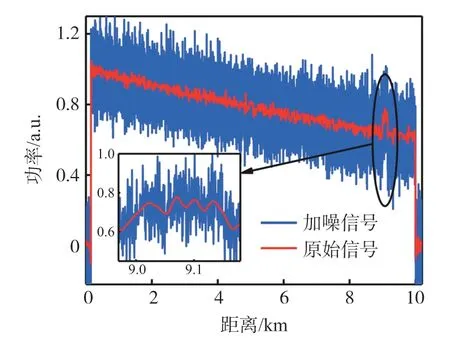
圖4 降噪前后單頻點功率時序仿真曲線

為了準確評估降噪效果，抽取變溫區域時序曲線數據，并計算其均方根誤差(Root Mean Square Error，RMSE)進行對比。不同參數下每條時序曲線重復仿真10 次，計算10 次的溫度改變區RMSE 平均值。設置高斯白噪聲功率分別為-10 dBm、-5 dBm、0 dBm、5 dBm、10 dBm，將小波分解層數設置為1～6，所得不同分解層數下變溫區的RMSE 分布如圖5 所示。

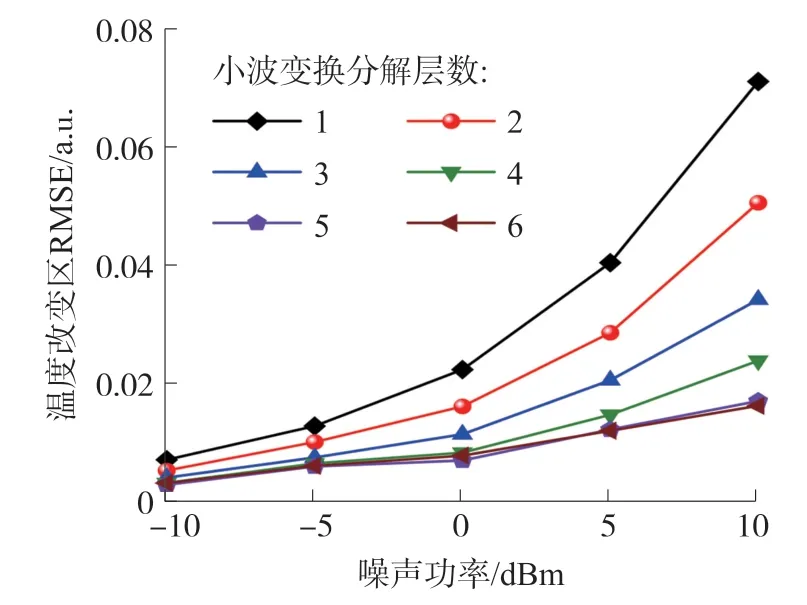
圖5 不同分解層數下變溫區的RMSE 分布

由圖5 可以看出，隨著噪聲功率的增大，降噪后曲線變溫區的RMSE 開始上升，即測量誤差增大，降噪效果開始下降。在噪聲功率一定時，隨著分解層數的增大，RMSE 值逐漸減小，這一現象在高噪聲功率下表現更加明顯。但當分解層數為5 和6 時，RMSE 基本相同，降噪效果區別不大，考慮到數據計算量及處理時間，選擇小波分解層數為5。

此外，針對不同的小波基函數與消失矩階數，進行了仿真研究，討論其對降噪效果的影響。仿真研究中，高斯白噪聲功率為10 dBm，閾值處理規則仍采用minimax 軟閾值處理，分解層數為5，采用常用的小波基函數dbN、symN、coifN，設置消失矩階數為1～5，不同小波基函數和消失矩階數下所得的仿真結果變溫區RMSE 分布如圖6 所示。可以看出，采用sym5 小波基函數獲得的RMSE 值最小，降噪效果最佳。

圖6 不同小波基函數及消失矩階數下的RMSE 分布

通過上述仿真研究，在基于微波外差掃頻的BOTDR 系統中，小波閾值去噪方案參數可設置為:小波基函數為sym5，分解層數為5，閾值規則為minimaxi 軟閾值處理，在此設置下降噪效果較優。基于上述最優參數匹配的小波閾值降噪方案，對前述圖3 中所示的噪聲功率為10 dBm 下的BOTDR 三維BGS 進行降噪處理，處理結果如圖7 所示。可明顯看出，經小波閾值降噪后，布里淵增益譜整體波動顯著減小，之前和噪聲混淆在一起的變溫區域可以清晰還原。

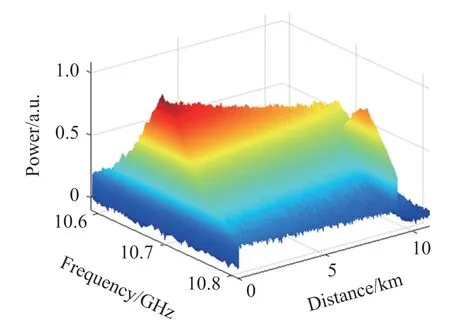
圖7 降噪三維BGS 仿真結果

分別針對降噪前(圖3 所示)和降噪后(圖7 所示)的仿真三維BGS 進行洛倫茲擬合和尋峰處理，可獲得降噪前后的仿真BFS 分布曲線，如圖8 所示。可明顯看出，采用小波閾值降噪后，整體的BFS分布波動顯著減小。同樣，在放大的變溫區細節中，也可觀察到BFS 噪聲得到明顯抑制，測試精度大幅度提高。

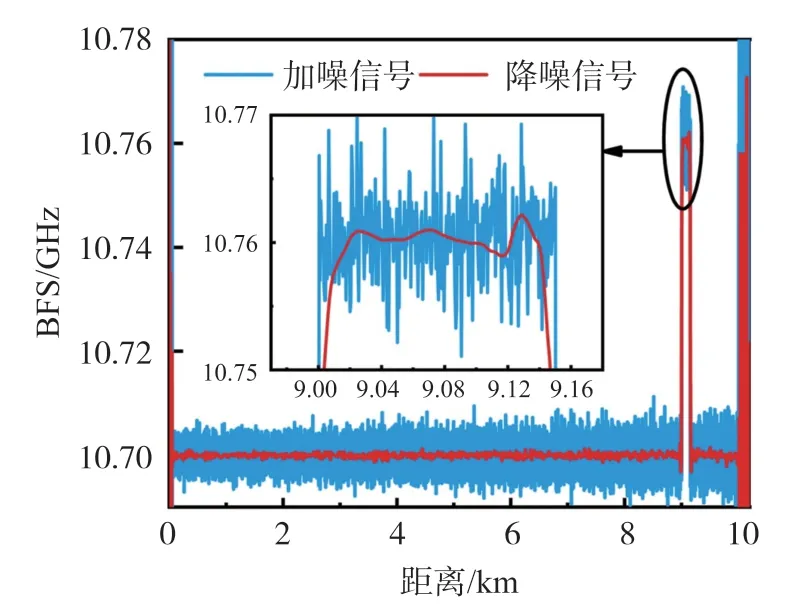
圖8 降噪前后BFS 仿真曲線

此外，提取仿真結果中變溫區同一位置處的布里淵增益譜原始信號、加噪信號和降噪信號，對比結果如圖9 所示。可以看出，加入高斯白噪聲后，布里淵增益譜出現明顯較大的幅度波動。經小波閾值降噪后，白噪聲引起的布里淵增益譜波動可以得到很好的抑制，原始的增益譜譜形得到了很好的還原，從而提高了BFS 分布測試精度。因此，本文采用的小波閾值降噪方案對于FS-BOTDR 系統具有較好的噪聲抑制效果，下面將結合實際BOTDR 溫度測量實驗進一步研究。

圖9 同一位置處的原始、加噪和降噪BGS 仿真結果

2 小波閾值降噪實驗研究

2.1 BOTDR 溫度測量系統

基于微波外差掃頻BOTDR 原理，搭建了如圖10所示的實驗裝置圖，整個系統由光學鏈路與電學鏈路構成。在圖10(a)所示的光學鏈路中，激光器輸出的連續光由耦合器分為10%和90%兩路，10%一路作為本征參考光，90%一路經過光脈沖調制模塊生成探測脈沖光。探測脈沖光通過EDFA 放大后，經環形器注入傳感光纖。探測脈沖光在傳感光纖中產生后向自發布里淵散射，經過EDFA 放大后與參考光通過1 ∶1 耦合器進入光電探測器中進行相干拍頻。其中，為了減少相干探測系統的偏振噪聲影響，在本征參考光中添加了擾偏器。

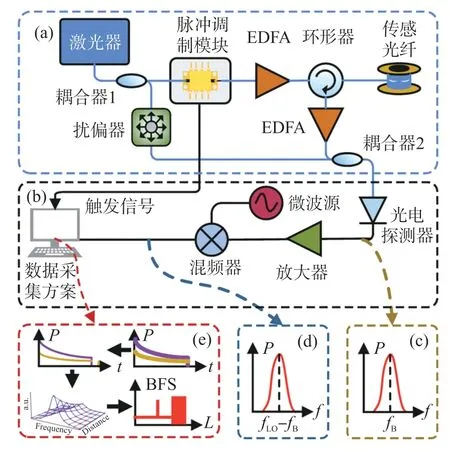
圖10 BOTDR 實驗裝置圖

圖10(b)所示為電學鏈路。光電探測器輸出中心頻率為fB的拍頻電信號，放大后通過混頻器與微波源輸出信號進行下移頻降至中頻，頻率為fLO-fB，其中fLO為微波源輸出正弦信號頻率。混頻后得到的中頻信號進入數據采集與處理系統。在數據采集過程中，通過步進改變微波源輸出頻率，采集每條單個頻率點下的功率時序曲線，進行累加平均和小波閾值降噪處理。將降噪后的所有單頻功率曲線合成三維BGS，按照距離域將不同掃描頻率點的功率值進行歸一化和洛倫茲擬合，最后獲取待測光纖的布里淵頻移分布曲線。

實驗參數設置如下:傳感光纖為G652D 單模光纖，總長度約為10 km，常溫25 ℃下固有布里淵頻移約為10.712 GHz。探測脈沖光寬度為50 ns，脈沖重復頻率為8 kHz，選取光纖末端約150 m 光纖(9 000 m～9 150 m)置于恒溫箱中，恒溫箱溫度設置為55 ℃，其他待測光纖置于室溫25 ℃下。

2.2 小波閾值降噪效果分析

首先從單頻功率曲線來驗證上述降噪算法的有效性。實驗中將微波源頻率輸出固定為10.745 GHz(對應恒溫箱溫度55 ℃)，采集該頻率點下的單頻功率曲線，實驗中單頻曲線平均累加次數為200，歸一化后采用前述小波閾值降噪算法進行降噪處理，所得的原始信號和降噪信號如圖11 所示。可以看出，由于掃描頻率與變溫區光纖布里淵頻移匹配，因此變溫區(9 000 m～9150 m)功率明顯大于室溫區，變溫區出現功率尖峰(由于放大器增益為負斜率，因此尖峰向下)。對比原始信號和降噪信號可明顯看出，經過小波閾值降噪后，室溫區和變溫區的單頻曲線波動均減小，即噪聲得到了有效抑制。

圖11 10.745 GHz 單頻點功率曲線原始與降噪信號

進一步從三維BGS 分布來驗證降噪算法的有效性。實驗中，通過步進調整微波源輸出頻率進行掃頻測量，起始頻率設置為10.59 GHz，終止頻率設置為10.81 GHz，步進間隔為5 MHz，每個掃頻點下的功率曲線平均累加次數為200。將采集到的每個頻率點下的功率時序曲線按照掃頻點順序依次排列，歸一化后的原始三維BGS 分布如圖12 所示。可以看到，原始三維BGS 中的變溫區受到噪聲影響，并未呈現出較明顯的尖峰，難以準確識別。

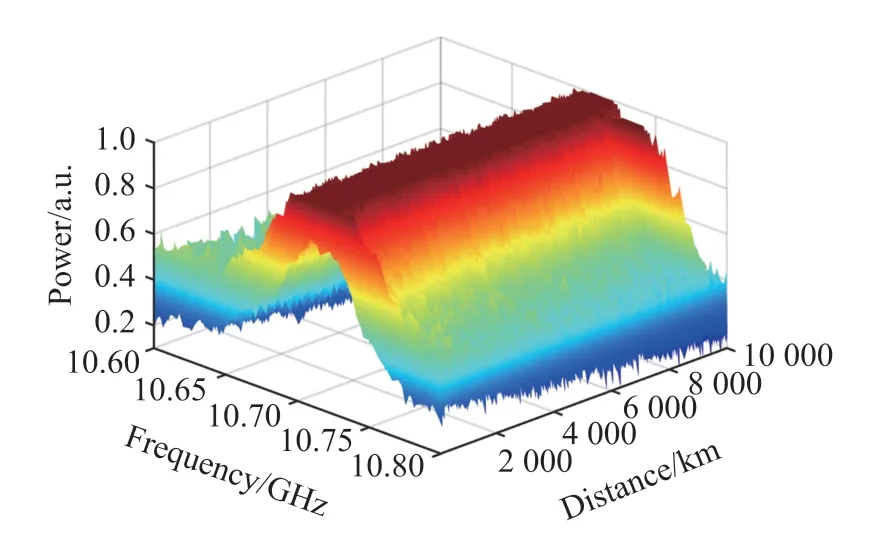
圖12 原始三維BGS

基于小波閾值降噪算法對圖12 中的每條單頻功率曲線進行降噪處理，可得到如圖13 所示的降噪三維布里淵增益譜。可以看出，相比于原始信號，經過降噪處理后變溫區尖峰明顯，可較為準確地還原溫度變化。

圖13 降噪后三維BGS

分別針對降噪前和降噪后的三維布里淵增益譜進行洛倫茲擬合，得到對應的光纖沿程BFS 分布曲線，如圖14 所示。分析降噪前后數據所得的BFS 曲線可知，經過小波閾值降噪后，從整體趨勢來看變溫區和室溫區的測量噪聲均得到明顯抑制。為進一步評估降噪效果，以變溫區BFS 數據為研究對象，分別計算了降噪前后變溫區的波動極差和RMSE。結果表明，在同樣的測量條件下，經過小波閾值降噪后，RMSE 由1.2 MHz 降低至0.16 MHz。變溫區BFS 波動極差從5.8 MHz 降低至3.2 MHz，實驗所用光纖的布里淵頻移溫度線性系數為1.14 MHz/℃[20]，代入計算可得測溫精度由±2.545 ℃提升至±1.4 ℃。

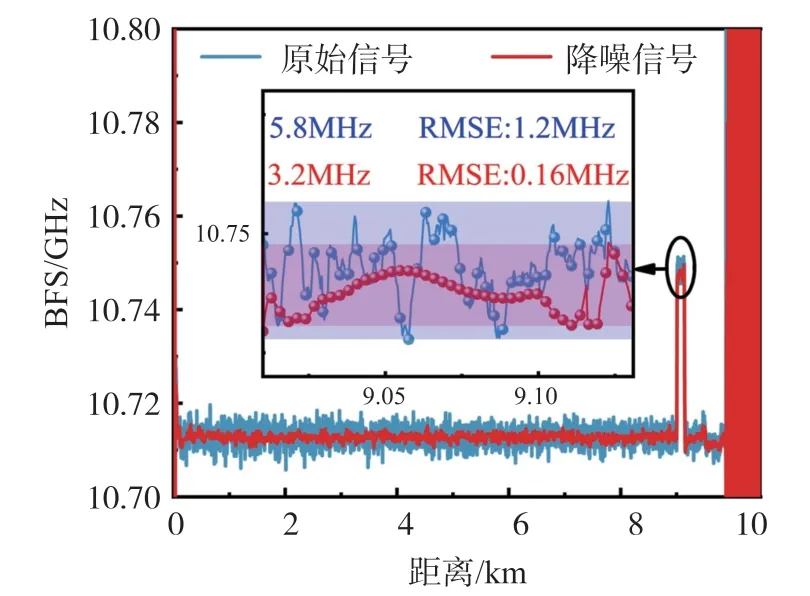
圖14 降噪前后BFS 分布

圖15 所示為變溫區中心位置處的原始和降噪后的布里淵增益譜對比圖。可以看出，經過小波閾值降噪后，布里淵增益譜幅值波動減小，進一步證明小波閾值降噪可抑制各個掃頻點功率曲線的噪聲，為布里淵增益譜的洛倫茲擬合運算提供高精度數據源，從而最終提高BOTDR 測量精度。

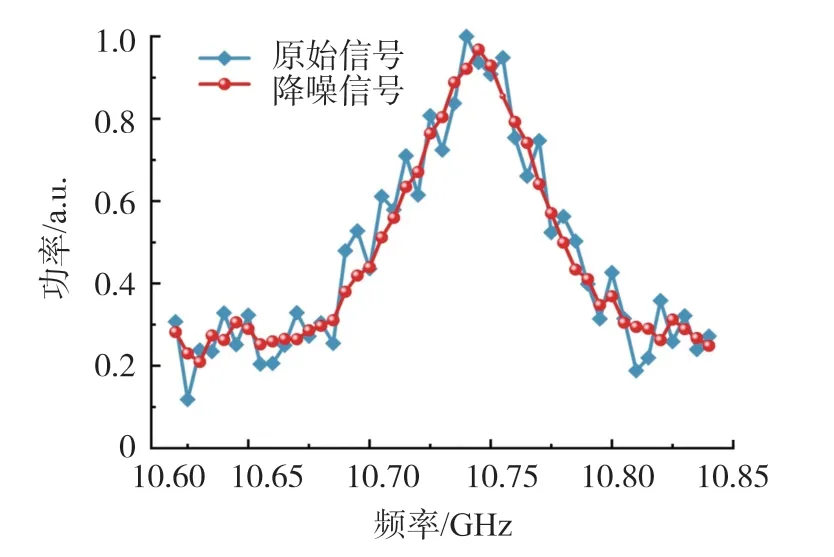
圖15 降噪前后變溫區中心位置處BGS

3 結論

本文針對微波外差掃頻BOTDR 系統中存在的信噪比較低問題，采用小波閾值降噪算法對掃頻測量過程中的每條單頻曲線進行噪聲抑制，最終提高BOTDR 測量精度。首先搭建了基于微波外差掃頻原理的BOTDR 單頻曲線和三維BGS 仿真模型，通過仿真研究討論了不同小波基函數、小波基變換分解層數及消失矩階數對測量精度的影響，優化了小波閾值降噪方案參數。最后搭建微波掃頻BOTDR 實驗平臺，對約10 km 的傳感光纖末端進行測溫實驗。實驗結果證明，當每條單頻曲線平均累加次數為200 時，采用本文優化的小波閾值降噪方案，使得變溫區的布里淵頻移波動極差從5.8 MHz 降低至3.2 MHz，均方根誤差由1.2 MHz 降低至0.16 MHz，測溫精度由±2.545 ℃提升至±1.4 ℃，布里淵增益譜的幅值波動也得到有效抑制。理論仿真和實驗研究證明，采用優化的小波閾值降噪可提升BOTDR 測溫精度。