可調焦雙穩系統隨機共振特性及應用研究*

黃玉楊，黃詠梅，林 敏

(中國計量大學計量測試工程學院，浙江 杭州 310018)

近年來，非線性科學不斷發展，隨機共振理論為強噪聲背景下微弱信號檢測提供了新方法。但是，隨機共振需要信號、噪聲和系統三者協同作用才能產生[1]。為了使隨機共振能更好地應用于工程實際信號處理，人們相繼提出了二次采樣[2]、雙調制[3]、尺度變換[4]、參數調節[5]等方法，應用于旋轉機械故障檢測[6]、低濃度氣體檢測[7]、液體成分檢測[8]、圖像增強[9]等領域。

經典雙穩勢函數是目前應用最為廣泛的勢函數，針對勢函數存在的飽和特性，趙文禮等提出了不同類型的分段勢函數，以雙穩勢函數的勢阱底或勢壘頂位置作為分段點，每段函數分別采用一次函數[10-11]、二次函數[12]、指數函數[13]等形式。這些勢函數通過改變經典雙穩勢函數外側的非線性形式來影響飽和特性和輸出信號的幅值大小。但隨機共振效應的強弱并非由輸出信號的幅值大小決定，而是由系統的非線性與噪聲相互作用產生的輸出信號信噪比大小決定。因此，需要考慮無序的噪聲與勢函數作用產生的能量聚集，而具有焦點的拋物線型勢函數則有著能量聚集的特性。

為增強隨機共振效應，提高系統能量聚集能力，構建一外側曲線為拋物線的勢函數，通過調節拋物線焦距，改變系統非線性特性，特別是能量的聚集能力，建立焦距與Kramers 逃逸率和輸出信噪比的解析式，分析了焦距對系統的飽和特性以及隨機共振效應的影響，通過焦距的調節可以控制微弱信號和噪聲相互作用，提高系統輸出信噪比。

將該系統用于渦街流量計信號處理，以輸出信噪比作為衡量指標，通過遺傳算法自適應調節焦距等參數，提高小流量渦街信號的輸出信噪比，準確獲取渦街信號頻率。

1 可調焦雙穩勢函數

受到周期信號S(t)與噪聲N(t)作用的雙穩系統可以由Langevin 方程描述:

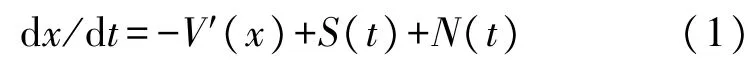
式中，S(t)＝A0cos(2πf0t)為輸入的周期信號，其中A0為信號幅值，f0為信號頻率；N(t)為高斯白噪聲；經典雙穩勢函數V(x)如式(2):

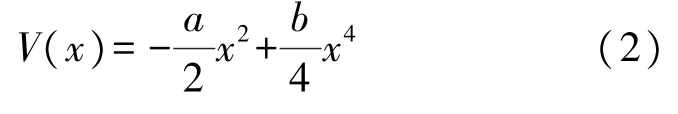
式中，a、b為勢函數的參數，經典雙穩勢函數有兩個穩定點，位置為，分別對應兩勢阱底部的位置，勢阱寬度，有一個不穩定點，位置為xn＝0，勢壘高度h＝a2/4b。

當x較大時，勢函數V(x)中x的四次方項起主要作用，x的微小增加使勢能快速增大。因此在經典雙穩系統中，當輸出信號幅值到達一定程度時，系統出現飽和現象。

構建可調焦雙穩勢函數U(x)可用式(3)表示，當a＝1、b＝1、P＝1 時，對應的曲線如圖1 所示。

圖1 可調焦雙穩勢函數曲線

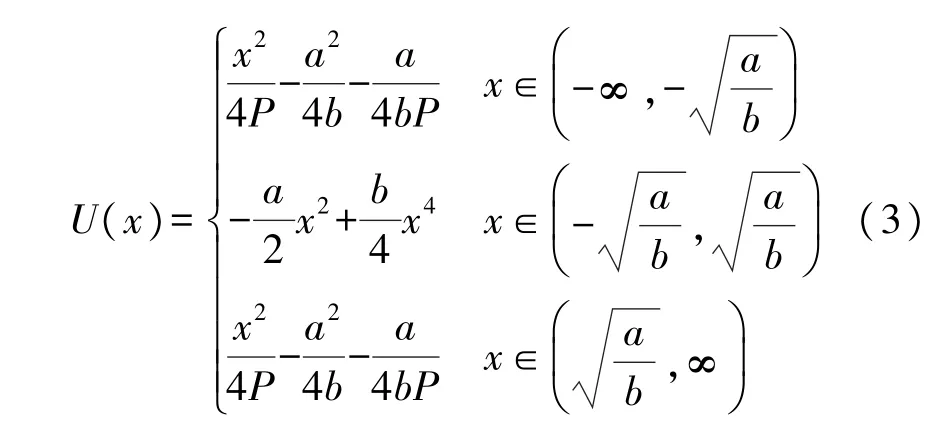
該勢函數以經典雙穩勢函數兩穩定點為分界點，外側為拋物線，其焦距為P，大小可調，內側保持原經典雙穩勢函數形式，將經典雙穩勢函數外側的勢能與位移之間的四次方關系轉換為二次方關系。勢函數外側對應拋物線頂點位置為(0，-a2/4ba4bP)，焦點F位置為(0，P-a2/4b-a4bP)。當焦距P分別為1、2、3 時，對應勢函數曲線如圖2 所示。焦距P增大，拋物線焦點向上移動，勢函數外側開度增大，焦距P減小，則反之，當焦距P過大時，勢函數外側趨于水平，不具有雙穩結構。可見，調節焦距P的大小可直接改變拋物線形狀，從而改變系統的非線性形式，進而改變信號、噪聲與系統的協同作用及能量的聚集。

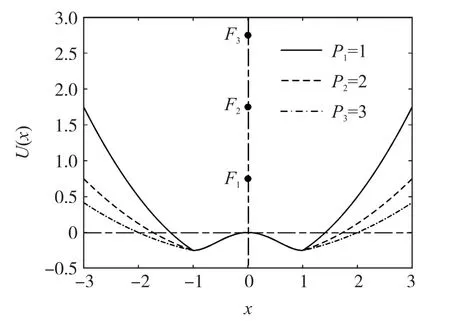
圖2 不同焦距下可調焦雙穩系統勢函數曲線

2 焦距大小與隨機共振效應

2.1 Kramers 逃逸率

雙穩態系統在兩個穩態間發生躍遷的速度，即為Kramers 逃逸率R。不同勢函數的Kramers 逃逸率不同，因此系統對微弱周期信號的響應速率不同。Kramers 逃逸率越大，非線性系統能檢測的周期信號頻率范圍越寬[14]。

從右勢阱底部出發的布朗粒子Kramers 逃逸率如式(4):

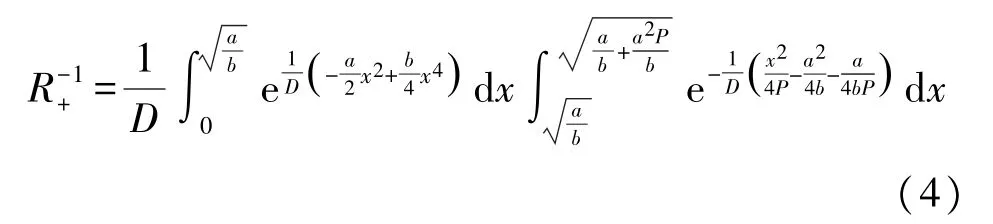
積分簡化計算可得式(5):

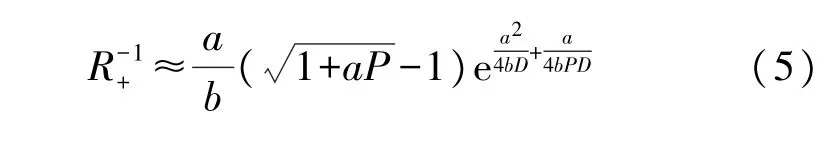
同理從左勢阱底部出發的布朗粒子Kramers 逃逸率如式(6):

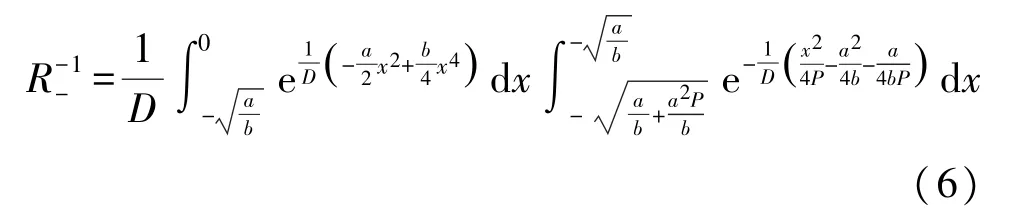
積分簡化計算可得式(7):

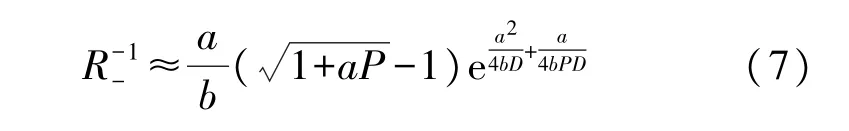
因此，可調焦雙穩勢函數的Kramers 逃逸率R如式(8):

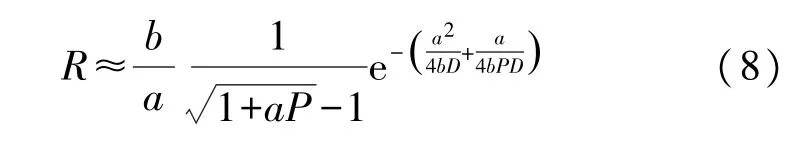
由式(8)可知，Kramers 逃逸率與焦距P密切相關。調節勢函數焦距的大小，可以改變Kramers 逃逸率。

參數a＝1、b＝1，當焦距P＝3，可調焦雙穩勢函數及經典雙穩勢函數的Kramers 逃逸率隨噪聲強度變化曲線如圖3 所示，可調焦雙穩系統的Kramers逃逸率明顯大于經典雙穩系統的Kramers 逃逸率，可調焦雙穩系統可以更好地與信號、噪聲匹配，擴大信號頻率的檢測范圍。

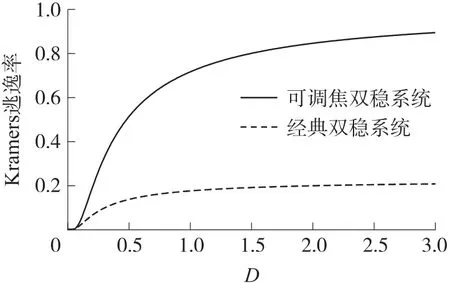
圖3 Kramers 逃逸率隨噪聲強度變化曲線

2.2 輸出信噪比

輸出信噪比SNR 是衡量隨機共振效應的重要參數。輸出信噪比SNR 計算式如式(9)所示。

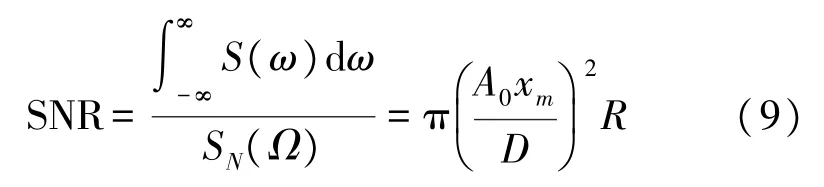
式中，S(ω)為信號的功率譜密度，SN(Ω)為噪聲平均功率，將式(8)代入式(9)中，可得式(10):

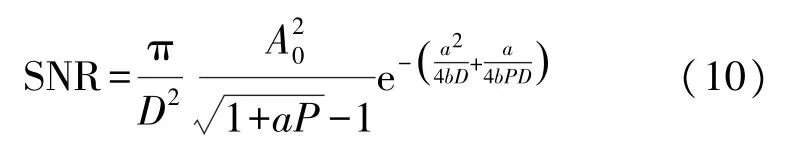
當信號幅值A0＝0.05，焦距P＝3，可調焦雙穩勢函數及經典雙穩勢函數的系統輸出信噪比隨噪聲強度變化曲線如圖4 所示，可見，隨著噪聲強度的變化，系統輸出信噪比呈現明顯的單峰曲線，且可調焦雙穩系統的輸出信噪比明顯大于經典雙穩系統的輸出信噪比，說明可調焦雙穩系統能提高對噪聲無序能量的利用率，將更多的噪聲能量轉移至有序的信號中。

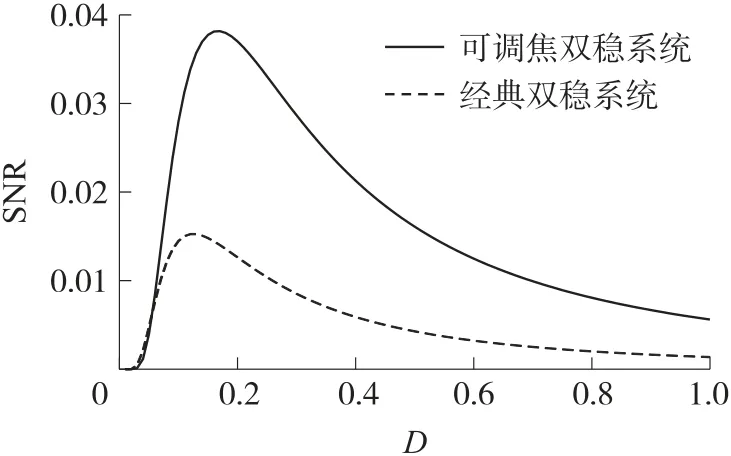
圖4 輸出信噪比隨噪聲強度變化理論曲線

當信號頻率f0＝0.01 Hz，信號幅值A0＝0.05，噪聲強度D＝0.2，可調焦雙穩系統的輸出信噪比SNR隨焦距P變化理論及仿真曲線如圖5 所示。理論與仿真曲線趨勢基本一致，隨著焦距P的變化，輸出信噪比呈現先增大后減小的單峰趨勢，表明存在一個使信噪比值最大的焦距P，能夠有效聚集能量，使非線性系統與信號、噪聲更好地匹配，從而增強系統的隨機共振效應。

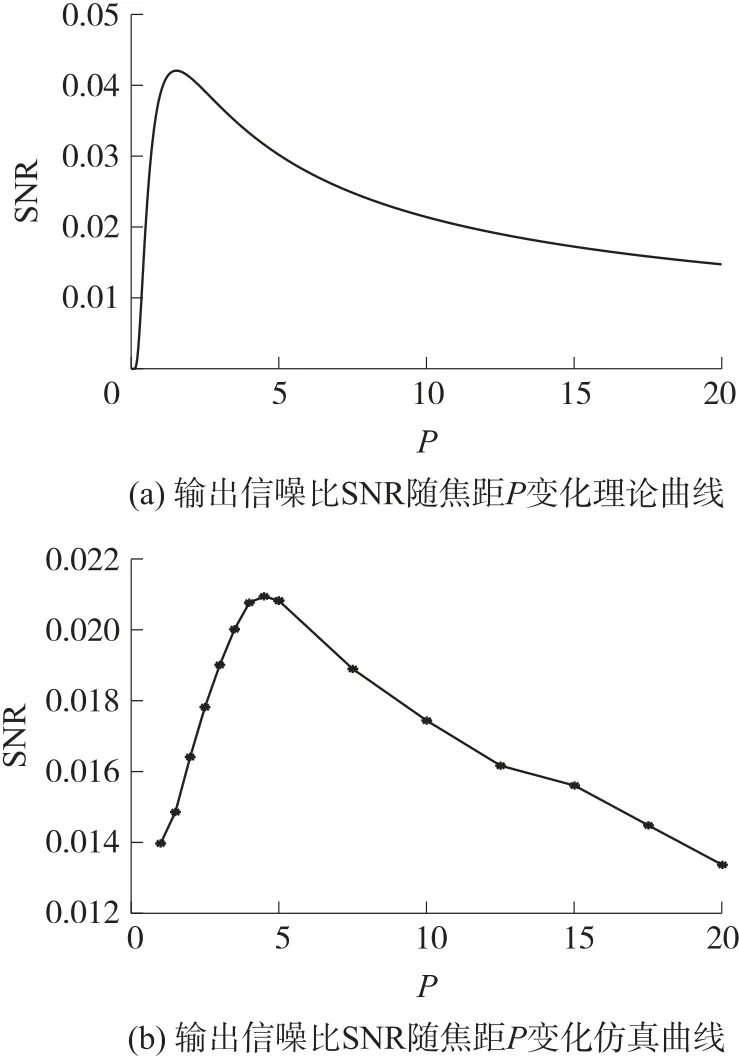
圖5 輸出信噪比SNR 隨焦距P 變化曲線

系統輸出信噪比的理論分析和數值仿真結果表明，調節焦距P的大小能影響系統能量的遷移，且存在最優的焦距P使得信噪比達到最大。

2.3 飽和特性的分析

當輸入信號幅值A0分別為0.5，0.75，1.0，1.25，輸入信號頻率f0＝0.01 Hz，噪聲強度D＝0，焦距P＝3時，不同勢函數下系統輸出信號時域圖如圖6 所示。從圖中可以看出，增大輸入信號幅值，對于經典雙穩系統，輸出信號的幅值基本不變，系統出現飽和現象，而可調焦雙穩系統的輸出幅值則隨著輸入的增加而增加，且輸出信號幅值大于經典雙穩系統。

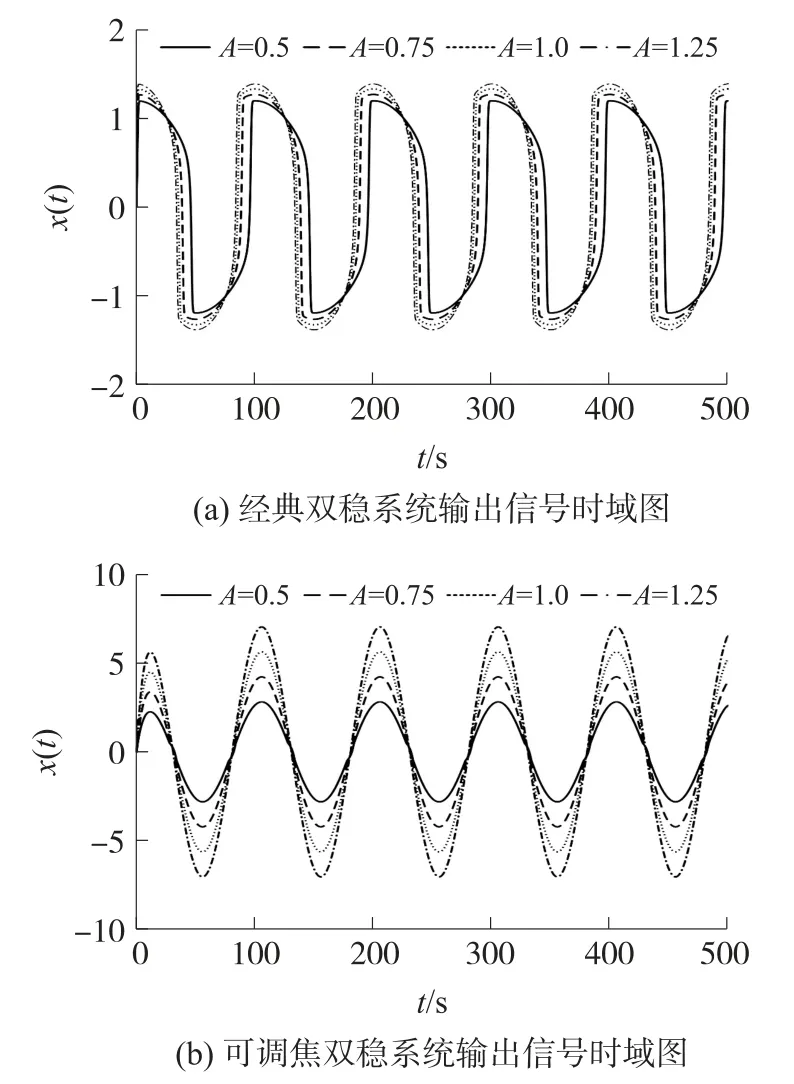
圖6 經典雙穩系統與可調焦雙穩系統輸出信號時域圖

3 基于遺傳算法的參數尋優及渦街信號處理

隨機共振效應與勢函數焦距密切相關，不同焦距具有不同的隨機共振效應，獲取最優焦距是隨機共振能否成功應用于工程信號處理的關鍵。遺傳算法是通過模擬達爾文進化論中優勝劣汰的規則自適應搜索最優解的方法，可進行多參數尋優，因此在應用于實際渦街信號處理中，通過遺傳算法對參數進行尋優。

3.1 渦街信號特點及信號預處理

渦街流量計是近幾年來發展較快的流量計之一，大多通過壓電傳感器測量漩渦壓力的周期變化得到管道中流體流速。在工業現場使用時，渦街信號容易受現場噪聲干擾，因此輸出信號由周期渦街信號及現場噪聲信號兩部分疊加而成，在小流量測量時，渦街信號容易被噪聲淹沒。渦街信號頻率f0與管道內流體流速Uv成正比[15]，旋渦頻率f0如式(11)所示:

式中，Sr為斯特勞哈爾數，d為旋渦發生體迎流面寬度，m為管道系數，在測量過程中，這些參數均為常數。

輸出信號幅值與旋渦升力對應，與管道內流體流速Uv成二次方關系，旋渦升力FL如式(12)所示:

式中，CL為渦街流量計升力系數，ρ為管道內流體密度。

當信號和噪聲作用于隨機共振系統，根據絕熱近似理論，在小參數條件下才有可能產生隨機共振，因此渦街信號直接輸入系統，并不一定與系統參數匹配，信號輸入系統前需要對信號進行預處理，對頻率進行調制，對幅值進行歸一化。

二語學習負動機現象是非英語專業大學生群體中較為普遍且難以解決的問題。本研究采用問卷調查的方式對非英語專業大學生的負動機現象進行實證研究，發現導致動機減弱的影響因素主要與學習者、學習環境和社會因素相關，在此基礎上還提出了有效的動機自我調控策略，無論是對二語教師的生態化教學還是對二語學習者的有效二語學習都將起到積極的促進作用。

信號頻率調制如式(13)所示:

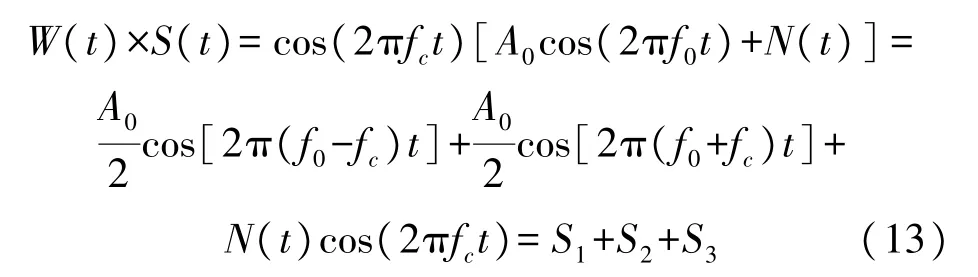
式中，S(t)為渦街流量計輸出信號，信號幅值為A0，N(t)為信號中疊加的噪聲信號，W(t)為調制信號，fc為調制信號頻率，信號調制后得到輸出信號S1、S2及S3，其中S1的信號頻率Δf＝f0-fc，調制信號頻率fc越接近被檢信號頻率f0，輸入到隨機共振系統的信號頻率越小，系統越容易產生隨機共振，S2和S3輸出相比S1非常微弱，可以忽略。

渦街流量計管道內介質流速大小不同，信號幅值會有較大變化，因此信號輸入隨機共振系統前對渦街信號進行歸一化處理，如式(14)所示:

式中，X′為歸一化處理后信號，X為原始渦街信號，Xˉ為原始渦街信號均值，δ為渦街信號標準差。

3.2 遺傳算法檢測步驟

輸出信號信噪比SNR 直接反應了隨機共振的強弱，因此以SNR 作為適應度函數篩選種群中的優劣個體。勢函數焦距P直接影響系統非線性，選取合適的P可利用更多噪聲能量，轉移至輸出信號中，增強輸出信噪比；調制信號的調制頻率越接近渦街信號頻率，越容易產生隨機共振，通過f0＝fc＋Δf，可以得到被檢信號頻率。因此使用遺傳算法對焦距P及調制信號頻率fc進行自適應尋優。圖7 為遺傳算法自適應尋優的流程圖。

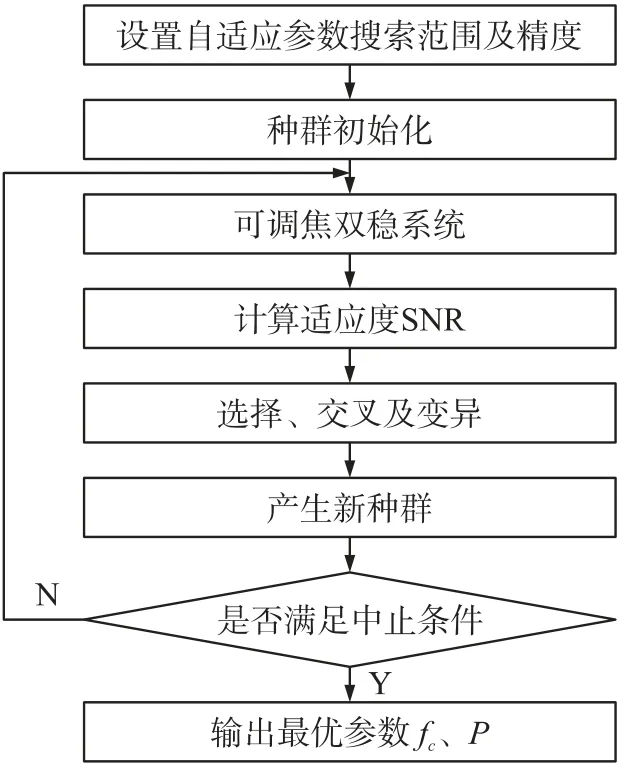
圖7 遺傳算法尋優流程圖

具體步驟如下:

對焦距P及調制信號頻率fc同時尋優，將兩參數對應的二進制編碼組成編碼長度為l的染色體。編碼長度分別設置為l1、l2，將其轉換為{al2＋l1al2＋l1-1…al1al1-1…a2a1}的染色體，待優化變量的區間為[xmin，xmax]，染色體可解碼還原，調制信號頻率fc的編碼長度設置為16，焦距P的編碼長度設置為8；

②種群初始化

隨機生成染色體，組成確定規模的初始種群。將種群規模N設置為100，進化代數M設置為40；

③遺傳、交叉與變異

計算個體適應度，選擇出優良參數串數據個體。進行染色體交叉及變異。將交叉概率設置為0.6，變異概率設置為0.05；

④終止

重復步驟③，判斷是否達到終止規則，若最佳適應度在M代沒有明顯變化，則視為收斂，輸出該種群中的最佳染色體，終止搜索，否則繼續迭代。

4 實驗結果與分析

4.1 實驗裝置

搭建渦街流量計實驗裝置如圖8 所示，通過工作量器給出標準體積。實驗裝置中渦街流量計精度為1.0，管道口徑為50 mm，流量計管道內發生體迎流面寬度為14 mm，該流量計的量程為60 m3/h，斯特勞哈爾數經實驗標定后為0.167 0。

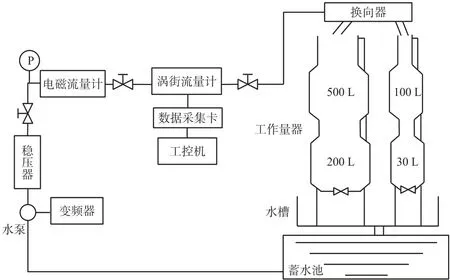
圖8 渦街流量計實驗裝置示意圖

4.2 數據處理與分析

選取小流量渦街信號進行實驗分析。信號采樣頻率為200 Hz，當流量為7.16 m3/h 時，采集到的渦街信號時域圖及頻域圖如圖9 所示，圖9(b)中信號功率譜峰值非常微弱。調制信號頻率fc的搜索范圍設置為[17，27]Hz，焦距P的搜索范圍設置為[0，20]，進行遺傳算法自適應尋優，得到最優調制信號頻率fc為18.396 6 Hz，最優焦距P為8.870 6，對應系統輸出時域及頻域圖如圖10 所示。從可調焦雙穩系統輸出時域圖中看出，渦街信號產生明顯周期性，從頻域圖中看出，信號的功率譜峰值明顯增強，產生隨機共振，產生共振時的差頻Δf＝0.002 3 Hz，該管道內流量的信號頻率f0＝fc＋Δf＝18.398 9 Hz，計算可得流量為7.12 m3/h，誤差為0.70%。實驗結果表明，通過可調焦雙穩系統產生的隨機共振能準確獲取渦街信號頻率。

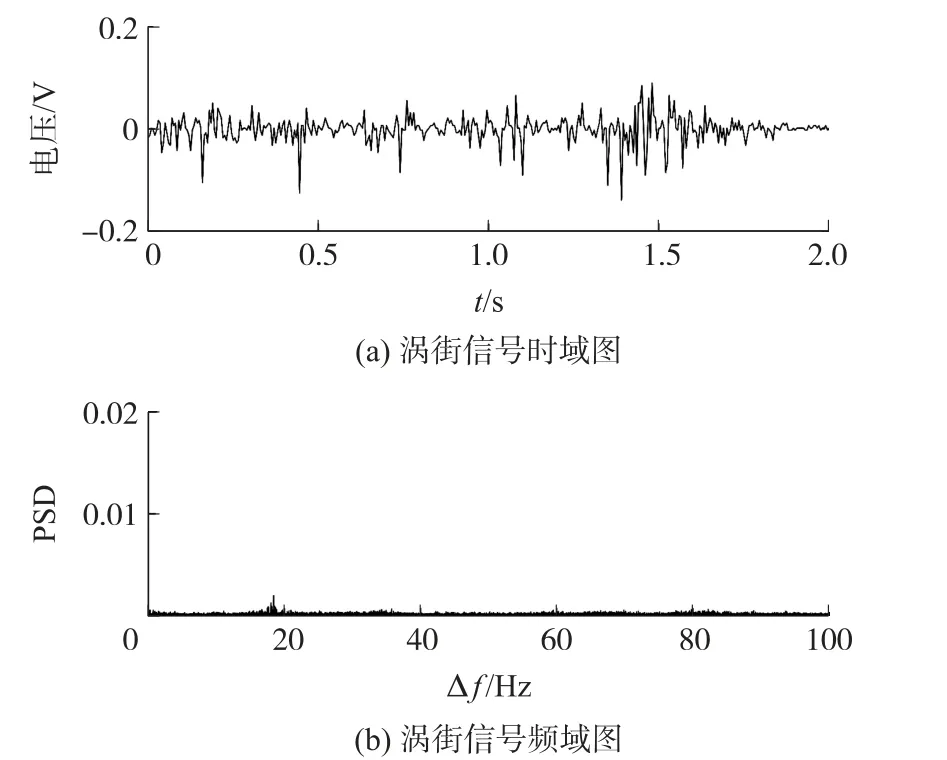
圖9 小流量渦街信號時域圖及頻域圖

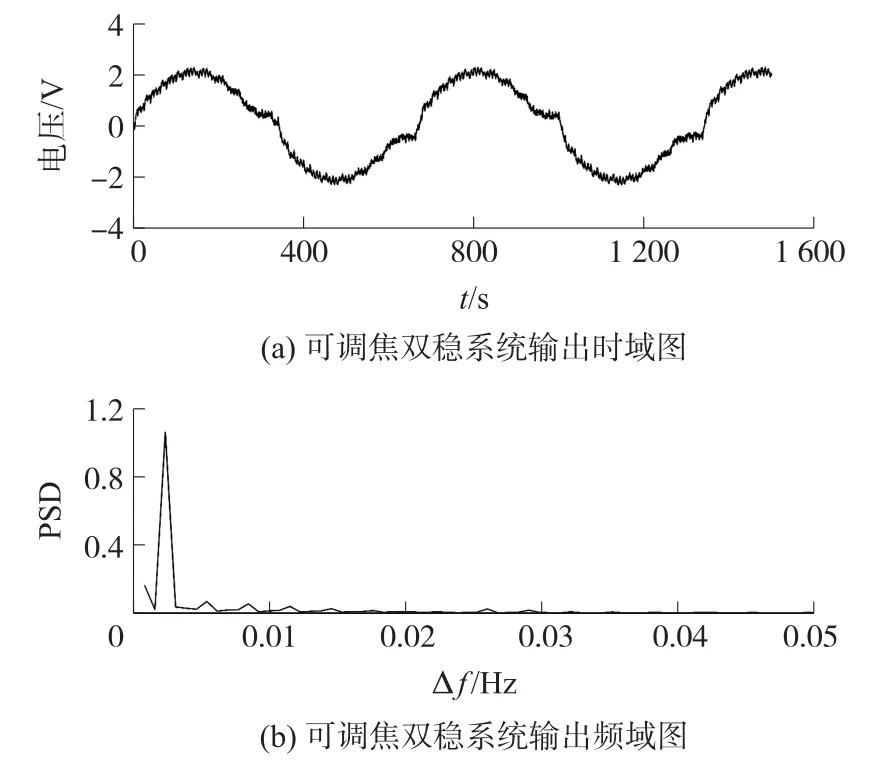
圖10 可調焦雙穩系統輸出時域圖及頻域圖

5 結論

隨機共振效應與勢函數形式及其參數有關，采用可調焦距的拋物線代替了經典雙穩勢函數兩外側的曲線，構建了一種新的可調焦雙穩勢函數，建立了勢函數焦距P與系統Kramers 逃逸率和輸出信噪比的近似解析關系，理論分析與數值仿真結果表明，調節焦距P可改變系統非線性特性，并且存在最優的焦距P能有效聚集能量，使輸出信噪比最大，隨機共振效應最為強烈。與經典雙穩勢函數相比，可調焦雙穩勢函數的隨機共振效應更強。將該系統應用于渦街信號處理，通過遺傳算法對勢函數焦距P等參數進行尋優。實驗結果表明，可調焦雙穩系統產生較強的隨機共振，能準確獲得小流量渦街信號頻率，具有較好的工程應用前景。