基于改進遺傳算法的航空器載重平衡

趙向領， 李云飛*， 李鵬飛

(1.中國民航大學空中交通管理學院， 天津 300300； 2.空軍某部隊， 武漢 430000)

近年來，隨著航空運輸業的快速發展，這種快速、高效、經濟的運輸方式深受客戶青睞，作為地面保障工作之一的配載平衡工作仍存在著優化空間。為保證飛機在投入運行后能夠實現安全且經濟的運行，同時便于飛行員輕松操縱，載重平衡工作成為亟待進一步研究優化解決的一個問題。為解決上述問題，現通過建立整數規劃模型，使用改進的遺傳算法進行求解，以期望使得上述目標能夠較好地滿足航司要求。

1 問題描述

某些最初設計為客機的飛機可以在必要時改裝成多用途飛機來運載貨物。特別是近期暴發的疫情更是加快了客機改裝進程。飛機所裝載的貨物類型可以是同類型的也可以是不同類型的。對于航空公司而言，飛機的配載問題是在考慮貨物體積和重量約束以及飛機結構約束的情況下，找到飛機上貨物的最優裝載分布，以實現飛機在運行過程中的平衡，確保飛機安全起飛和降落。

目前航空公司所存在的飛機載重平衡問題的本質是考慮如何合理地分配貨物到飛機的艙位，實現飛機重心位置最優和業載量最大。由于問題的復雜度較大，2015年Feng 等[1]在總結當前航空貨物運行的文獻時指出，飛機的配載問題是航空運輸中最基本的多項式非確定性問題(non-deterministic polynomial，NP)-難題組合優化問題之一。近年來在載重平衡問題的求解方法多集中在啟發式智能算法和快速發展的商用求解器上。

有關使用啟發式智能算法求解載重平衡問題的相關文獻有Dahmani 等[2-3]提出的多目標粒子群優化方法，將一組貨物分配到最小數量的集裝器中，然后將其放置到飛機特定的貨艙內，模型考慮了優化業載總重量和優先級；謝春生[4]運用遺傳算法建立了民航客機的裝載配平模型，并以B747客機為例開發了可視化軟件，解決了客機配載員工作強度大、效率低的問題；張洪[5]運用改進的蟻群算法開發了面向C919的配載優化系統；趙向領等[6]建立了民航客改貨飛機的載重配平模型，用于解決航空器配載問題，模型以運輸業載量最大和重心位置最優為目標，并運用遺傳算法進行的求解。谷潤平等[7]以貨機裝載重心最優為目標函數，建立了以重心、重量、結構等約束的混合整數規劃模型，依然使用遺傳算法求解；史永勝等[8]以貨機主貨艙為研究對象，建立了重心偏移量最小的目標函數以重心位置、貨艙結構、彎矩等為約束條件的整數規劃模型，運用遺傳算法進行求解；鄭琰等[9]研究了貨機群裝載非標準貨物的優化問題，建立了以重心率和空間利用率的目標函數模型，運用啟發式算法進行求解；陳璇等[10]采用自適應煙花算法對大型航空運輸機裝載優化模型求解，裝載模型考慮重量、重心、容積、系留等約束條件；孟超[11]針對民航寬體客機腹艙以綜合載重利用率和容積利用率最大為目標，運用啟發式算法和混和遺傳粒子群算法進行求解；白楊[12]分析了客機腹艙和全貨機載貨兩種情況的裝載特點，并建立混合整數規劃模型，使用基于有效空間的啟發式算法求解；朱賀[13]針對貨物需要送達同一目的地和貨物送到不同目的地，部分貨物在中途卸載或者空投的情況，采用了混合整數規劃模型分別對這兩種問題進行了建模，分別采用了精確求解和元啟發求解，并建立相應的軟件系統原型。

在使用商業求解載重平衡問題方面的文獻有Limbourg等[14]建立的以貨物力矩、飛機結構應力和燃油成本最小的混合整數線性規劃模型，可以將一組選定的貨物分配到飛機的預定位置，并以B747為研究對象使用商業求解器CPLEX驗證了模型的有效性；Verstichel等[15]及Vancroonenburg等[16]建立以裝載貨物價值最大和重心偏移量最小的雙目標規劃模型，用于解決B747貨艙中貨物裝載平衡的問題，使用Gurobi求解對比了人工配載專家的配載結果，驗證了模型的可行性和Gurobi的強大；Lurkin等[17]建立以燃油成本和操作成本最小的混合整數線性模型，考慮了飛機重心約束，用于解決在中間機場取貨和交付的飛機裝載問題，以B777為研究對象并使用IBM公司的CPLEX進行仿真驗證模型；Zhao等[18]把非線性重心包線描述為多段線性約束模型，并設計了線性化策略，在考慮位置、重量、平衡等約束條件下，建立了總業載最大、重心偏差最小的混合整數規劃模型。模型使用商業求解器CPLEX可在幾秒鐘內得到最優解，并且在所有測試實例中保持重心在指定的重心包線范圍內；李云飛等[19]使用Lingo求解器驗證了客改貨飛機的上下艙聯合載重平衡模型。

綜上所述，國內外對于載重平衡問題通常建立整數規劃模型，使用啟發式智能算法和商業求解器進行求解。但國內單獨對于載重平衡的研究較少，多數是將載重平衡問題作為研究航空貨運三維裝箱問題一個階段，考慮的約束不全面，致使模型不完整。另外對于客改貨這種新的運輸模式的載重平衡的研究還比較少。因此現運用改進的遺傳算法研究客改貨窄體機的載重平衡問題。

2 載重平衡模型構建

2.1 模型概述

根據目前的主流窄體機選定波音757-200為研究對象，為滿足貨艙業載量最大和重心偏移量最小的目標，需要建立貨艙的配載優化模型。

圖1是B757-200的貨艙側視圖，可以看出共有15個主貨艙、4個下貨艙。貨機的貨艙主要用來裝載集裝器，下貨艙裝載散貨，此次主要研究主貨艙的載重平衡問題。

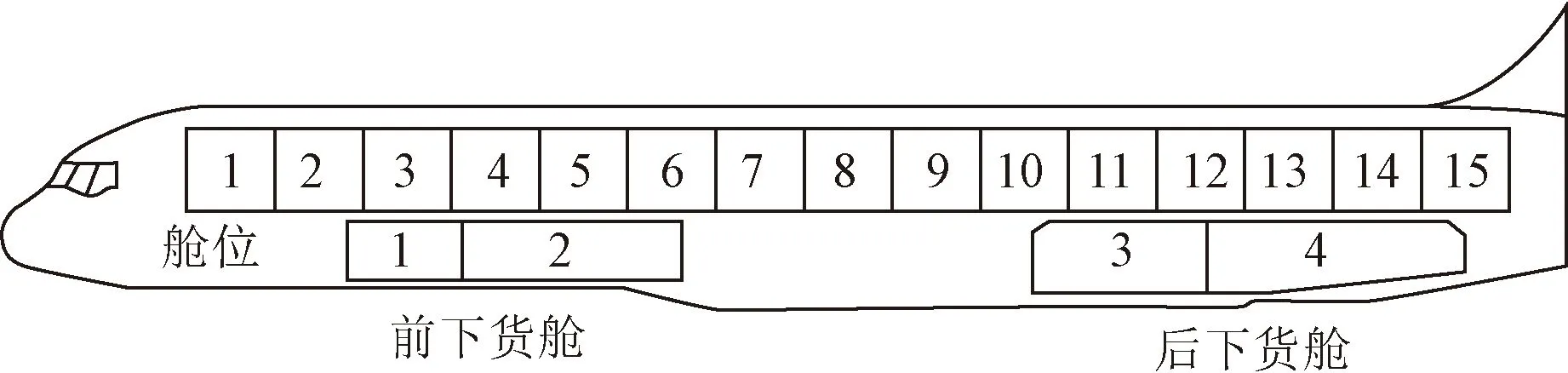
圖1 B757-200貨機側視圖Fig.1 Side view of B757-200 cargo plane

2.2 目標函數

在模型建立之前首先設決策變量xij為

(1)

式(1)中：i為第i個待裝載集裝器；j為第j個飛機貨艙艙位；NULD為待裝載集裝器總數；NPOS為飛機主貨艙可分配位置的總量。

為保證航空公司運輸利潤最大化和飛機運行安全，建立了以裝載量最大和重心偏移量最小的雙目標模型為

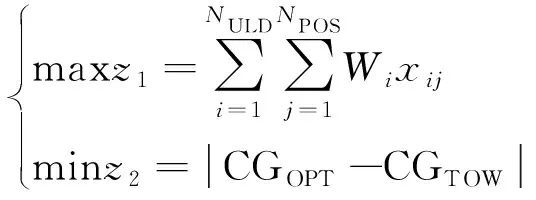
(2)

式(2)中：Wi為第i個待裝載集裝器的重量；CGOPT和CGTOW分別為飛機起飛最優重心和飛機在起飛重量(takeoff weight,TOW)時的重心，其中CGTOW的計算公式為

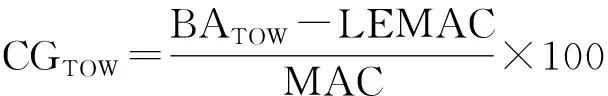
(3)

式(3)中：LEMAC為基準到平均空氣動力弦前緣的長度；MAC(mean aerodynamic chord)為平均空氣動力弦長；BATOW(balance arm)為起飛重量下的力臂值，計算公式為

(4)

式(4)中：OEW(operation empty weight)為飛機的空機重；BAOEW為飛機的空機重對應的力臂值；TFW(fuel weight)為飛機的起飛燃油重量；BATFW為燃油重量對應的力臂值；BAj為飛機第j個艙位的力臂值。

根據一線配載實際工作情況，現需要將雙目標函數冠以不同的權重ω1和ω2，且ω1+ω2=1，與此同時將目標函數做歸一化處理，將其轉化為單目標函數，即

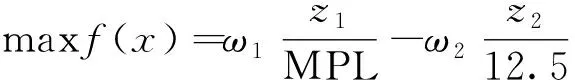
(5)

式(5)中：MPL(max pay load)為飛機的最大業載；12.5為重心包線前后限的一半，以%MAC表示。

2.3 約束條件

在對飛機貨艙集裝器裝載方案進行布局優化時，需要結合實際情況考慮約束，約束條件如下。

(1)保證每個集裝器最多放置在一個艙位內。

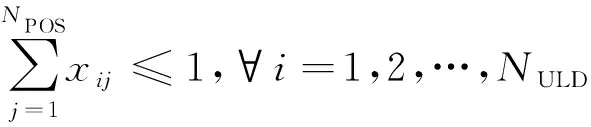
(6)

(2)每個艙位必須保證有一個集裝器。

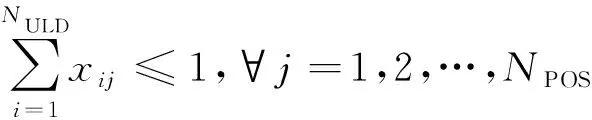
(7)

(3)集裝器重量應不超過集裝器所在艙位的最大重量。

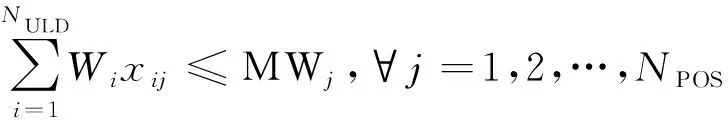
(8)

式(8)中：MWj為飛機第j個艙位的最大載荷。

(4)為保證集裝器可以完全裝載到貨艙內和飛機內壁不受損，貨艙內通常會有集裝器高度限制，所裝載的集裝器不能超過所在艙位能容納的最大高度。

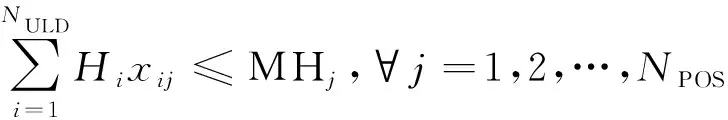
(9)

式(9)中：Hi為第i個待裝載集裝器的高度；MHj為第j個艙位的最大高度。

(5)飛機的主貨艙內一般還存在著分艙位區域限重，主要考慮1～5艙，6～10艙，11～15艙所在區域重量限重。

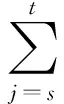
{(s,t)}∈{(1,5),(6,10),(11,15)}

(10)

式(10)中：MWst為主貨艙s到t艙的重量限制。

(6)飛機在運行中會受到最大無油重量(max zero fuel weight，MZFW)、最大起飛重量(max takeoff weight，MTOW)、最大著陸重量(max landing weight，MLW)的限制，儲備燃料重量(reserve fuel weight，RFW)為飛機的備用油量。

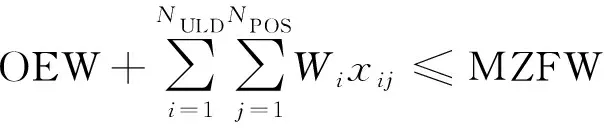
(11)

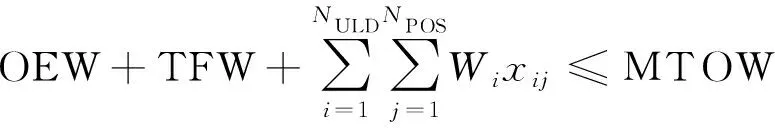
(12)

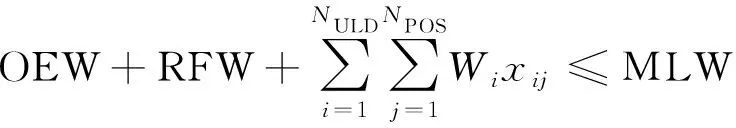
(13)

(7)飛機在運行中還會受到最大業載的限制。

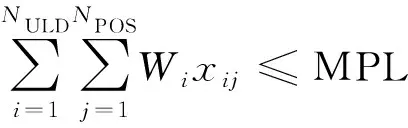
(14)

MPL的計算公式為

MPL=min{MZFW-OEW，MTOW-OEW-

TFW，MLW-OEW-RFW}

(15)

(8)為保證飛機的安全運行，飛機的重心必須時刻處于重心前后限的范圍之間。式(16)為飛機在不同重量下的重心限制，其中minINDw和maxINDw分別為飛機在不同重量下所對應的重心包線前后限，而INDw為在不同重量下配載結果對應的指數，通過式(17)計算獲得，即

(16)

w∈{TOW,LW,ZFW}

(17)

式中：BI為空機重指數；FIw為飛機不同重量時對應燃油指數；C1為縮小系數；CGDATUM為平衡基準點站位,對于給定航班為已知數據。

3 載重平衡問題求解

擬采用遺傳算法來求解載重平衡問題，遺傳算法是根據自然界的進化理論和遺傳學說所創造的一種啟發式算法。使用適者生存的原則來逐步逼近一個可行的近似解，這個過程使得新個體比原個體更能適應環境。圖2是遺傳算法流程圖。

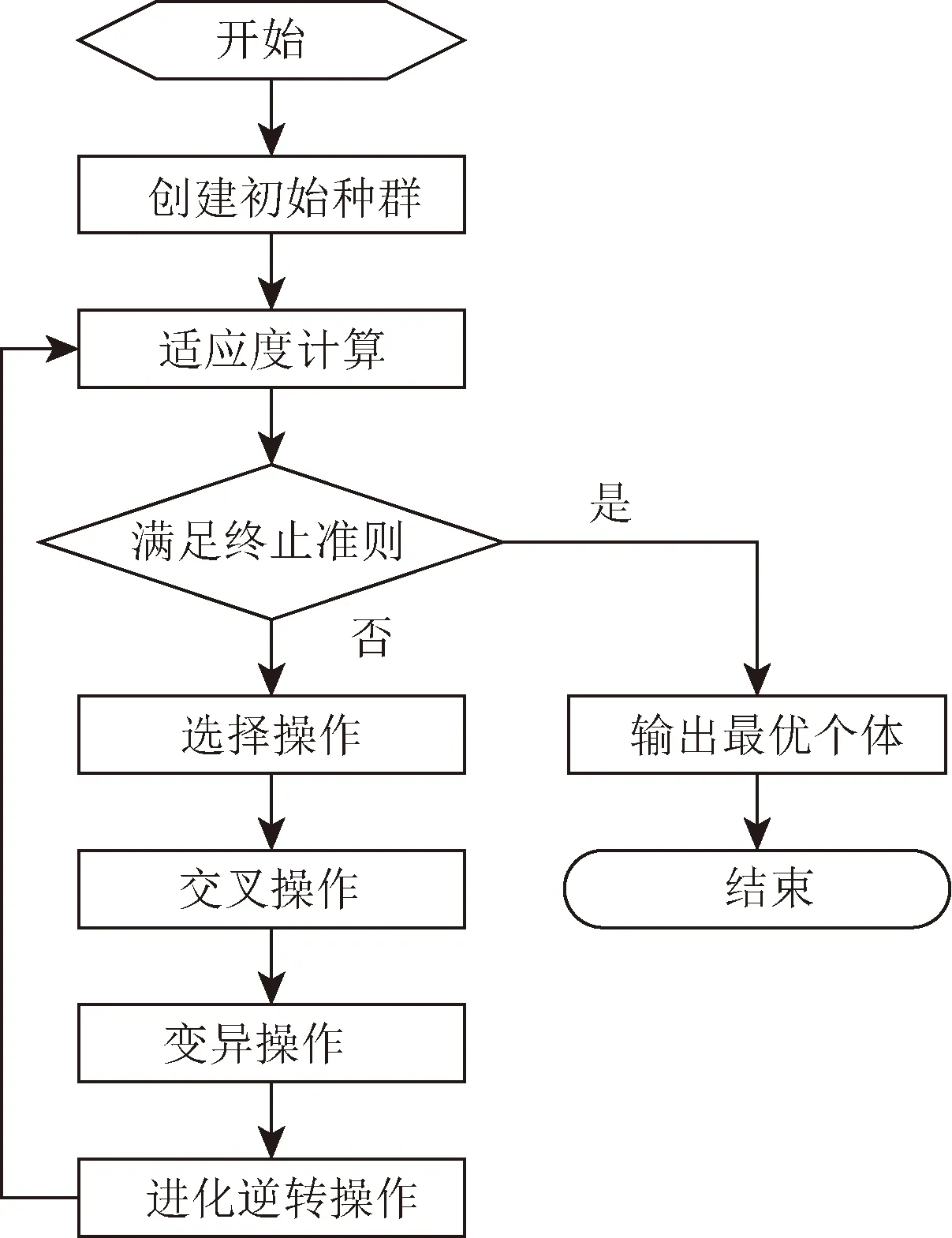
圖2 遺傳算法流程圖Fig.2 Genetic algorithm flow chart

3.1 編碼方式

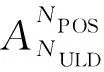
圖3 編碼方式示意圖Fig.3 Schematic diagram of coding mode

3.2 適應度函數

由于將雙目標函數轉化為單目標函數之后，仍是求解模型的最大值因此將目標函數[式(5)]作為適應度函數。

3.3 選擇算子

對于選擇算子的設計在這里仍采用常見的輪盤賭，輪盤賭是指個體被選中的概率與適應度成正比，適應度越高，個體被選中的概率越大。對于該模型而言，假設種群個體數為P,Fp為其中某個個體的適應度值，那么個體被選擇遺傳到下一代的概率Pp為

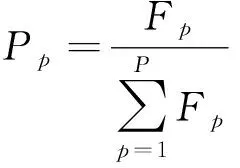
(18)

3.4 交叉算子

交叉操作是遺傳算法最重要的操作，是產生新個體的重要來源，直接關系到算法的全局尋優能力，采用部分映射交叉，即在滿足給定交叉概率下，隨機生成某條染色體上交叉位置。具體操作如下。

隨機產生兩個[1,10]的隨機數r1和r2，代表選擇交叉的位置，比如r1=2、r2=4,如圖4中灰色的位置，將第一個個體r1到r2之間的基因(即集裝器序號)與第二個個體r1到r2之間的基因交換，交換之后如圖5所示。

圖4 交叉前示意圖Fig.4 Schematic diagram of crossover

圖5 交叉后示意圖Fig.5 Schematic diagram after crossing

灰色部分表示交叉過來的基因，然而仔細觀察后發現交叉過來的基因與原來其他位置上的基因可能會有重復，第一個裝載方式重復基因的數目與第二個裝載方式重復基因的數目是相同的(這里都是3個)，只需要把第一個裝載方式重復的基因(用黑色標識)與第二個裝載方式重復的基因做交換，即可以消除沖突。消除沖突之后的解如圖6所示。

圖6 解除交叉沖突示意圖Fig.6 Schematic diagram for removing cross conflict

3.5 變異算子

變異算子的設計針對一個染色體(即個體)隨機選取兩個基因進行交換。例如圖7的變異示意圖，隨機生成區間[1，10]的兩個數r1、r2分別為3和8，然后將位置3和位置8互換基因。

圖7 變異算子示意圖Fig.7 Schematic diagram of mutation operator

3.6 進化逆轉操作算子

在標準的遺傳算法中是沒有進化逆轉操作算子的，為了加速進化在選擇、交叉、變異之后加入的一個操作。進化逆轉操作是具有單向性的，若逆轉之后個體變得更優即適應度越大，則執行逆轉操作，否則逆轉無效。逆轉算子在操作時仍是隨機選擇兩個位置r1和r2,然后將r1和r2之間的基因進行反向排序。比如對于某個裝載方式隨機選擇位置r1=3，r2=5，將其之間的基因按照相反順序倒過來。具體操作如圖8所示。

圖8 進化逆轉操作示意圖Fig.8 Schematic diagram of evolutionary reversal operation

在文獻[20-22]中，逆轉算子的加入使得子代繼承了更多的父代基因信息，由于只往好的方向逆轉，因此在搜索最優解的能力比順序交叉算子更強。

3.7 約束條件處理

在處理約束條件時運用文獻[23]中的y-check思想，具體過程為將每次的解代入各個約束條件中進行判斷。

約束(5)和約束(6)在編碼方式上已經處理完成無需考慮。

約束(7)和約束(8)在生成初始解就進行判斷，直到滿足約束(7)和約束(8)初始解輸出進行下一步工作。

計算目標函數，滿足約束(9)～約束(17)輸出解。

4 仿真實例

4.1 算例數據

某次航班任務執飛機型為B757-200F，飛行計劃報顯示此次飛行任務所帶起飛油量10 000 kg，航段耗油量為8 000 kg，表1給出了B757-200F的基本參數包括3類最大重量等，表2是每個艙位所能容納集裝器的最大重量和高度，表3為待裝載的集裝器基本信息。

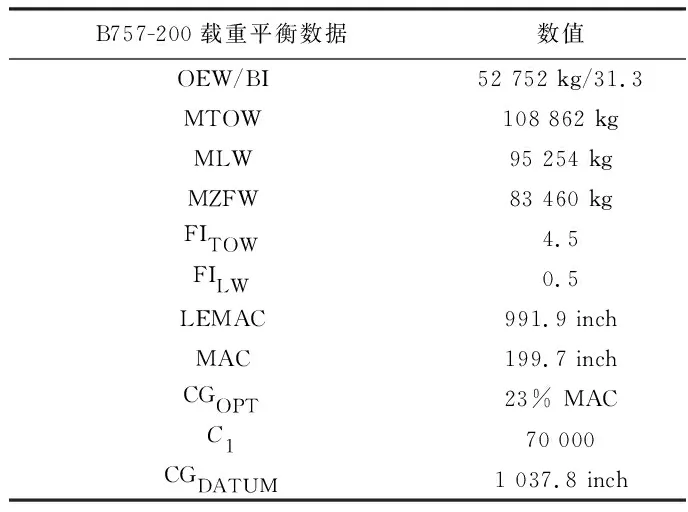
表1 B757-200F基本參數Table 1 Basic parameters of B757-200F

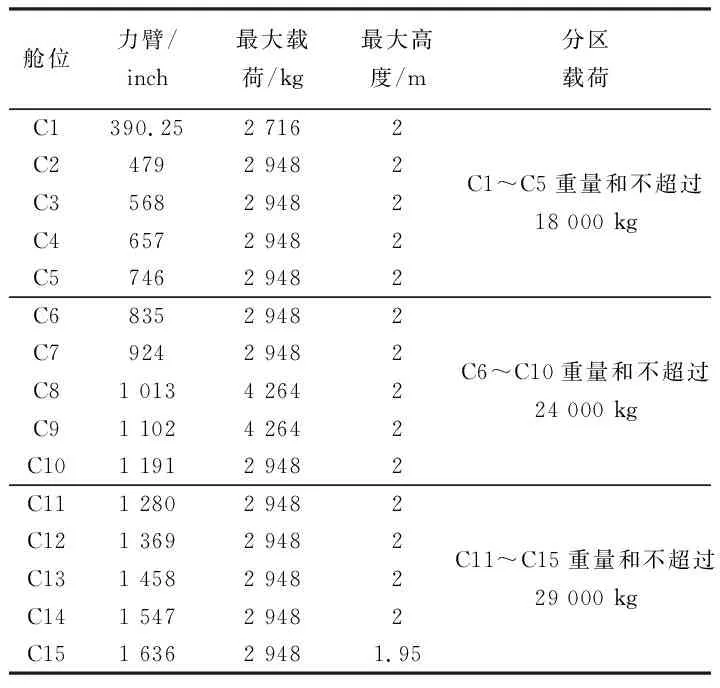
表2 貨艙艙位約束Table 2 Constraints in main cargo compartment

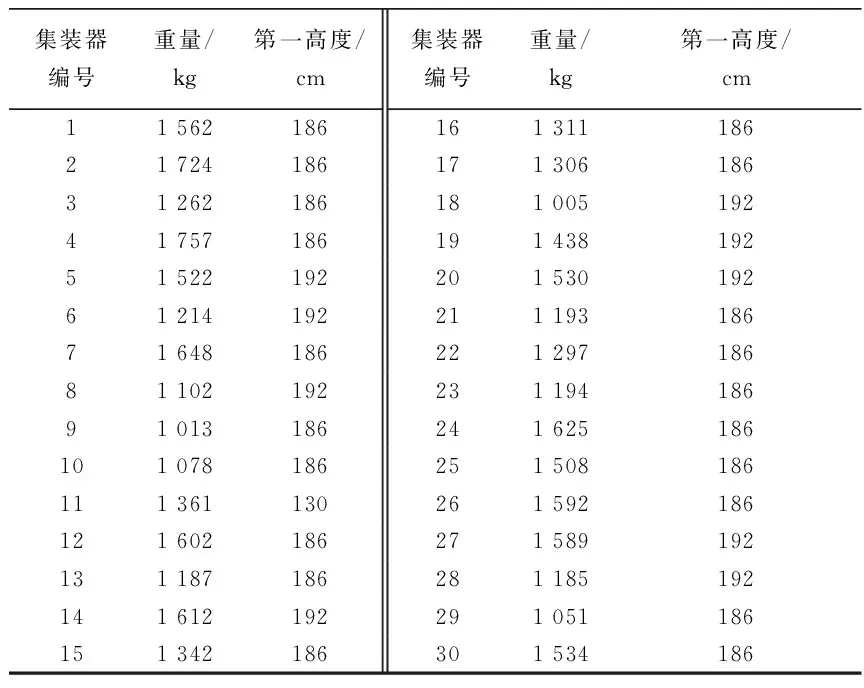
表3 集裝器重量、高度Table 3 Weight and height of ULD

4.2 算例計算

此次算法程序在Visual Studio 2019 下運行，設ω1=0.8，ω2=0.2，在遺傳算法中設置種群規模PS為200，遺傳進化代數Gen為200，交叉率PC為0.9，變異率PM為0.1，表4為計算結果，可知遺傳算法業載量平均為21 281 kg，重心偏移量平均為2.309%MAC，人工配載業載量為20 565.6 kg，重心偏移量平均為4.846%MAC。加入進化逆轉算子后只加快了收斂速度，所計算的結果與普通遺傳算法保持一致。

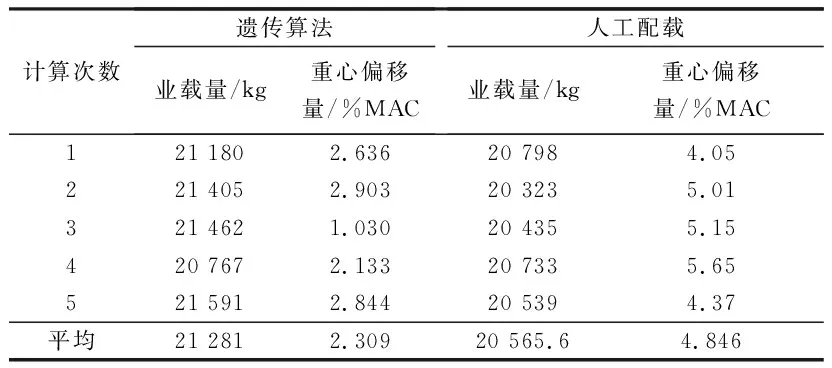
表4 計算結果Table 4 Calculation results

圖9是引入進化逆轉算子的遺傳算法和普通遺傳算法的適應度變化曲線，可以看出改進的遺傳算法可以較快得到目標值。

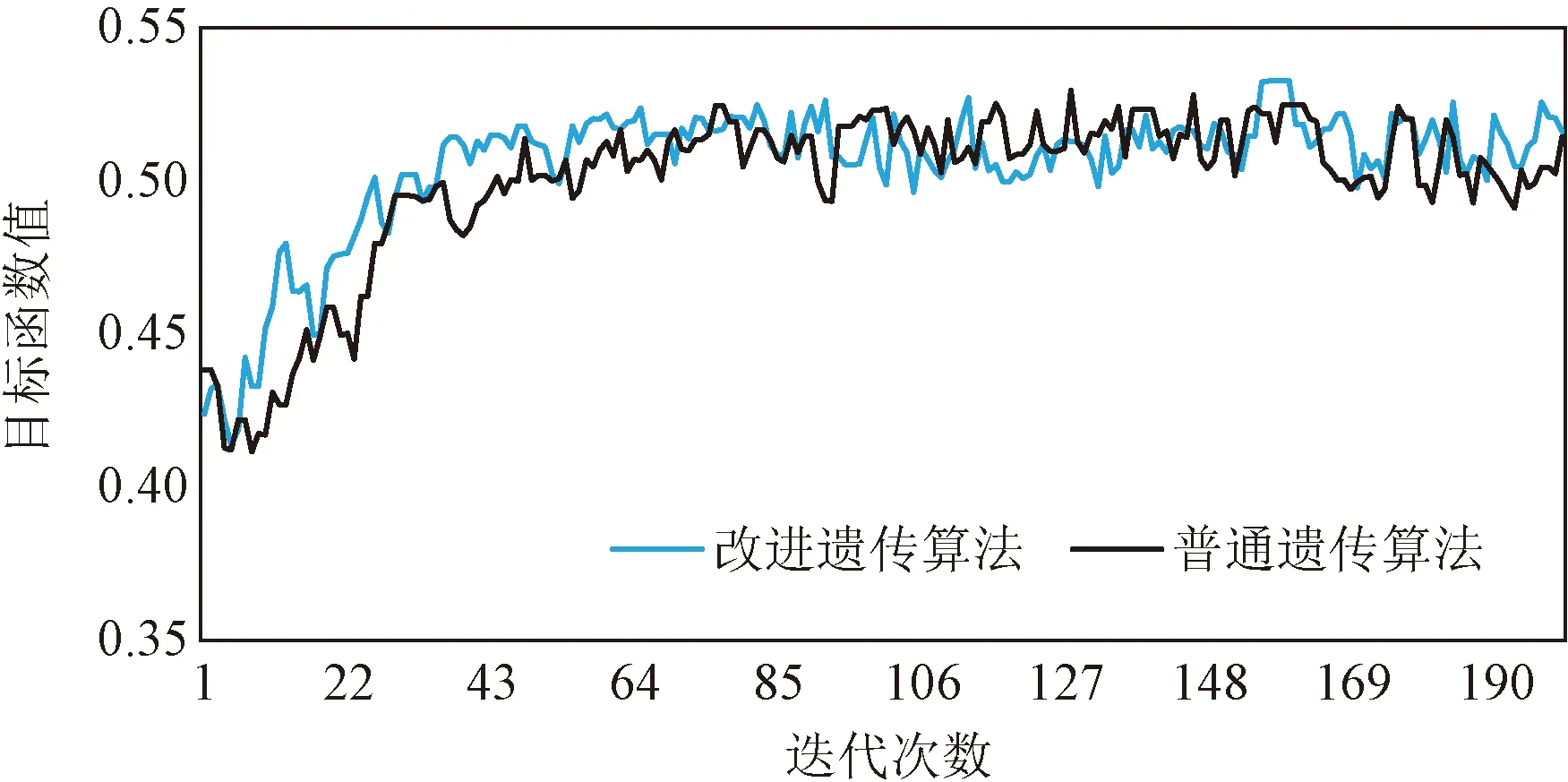
圖9 遺傳算法適應度變化曲線Fig.9 Fitness curve of genetic algorithm

圖10和圖11分別是在ω1=0.8下的重量箱線圖和重心偏移箱線圖，可以得出遺傳算法都要優于人工計算，這是因為運用遺傳算法時，可以快速排除質量較差的解，保留高質量的解，而人工配載一般根據經驗，不具有高效性。

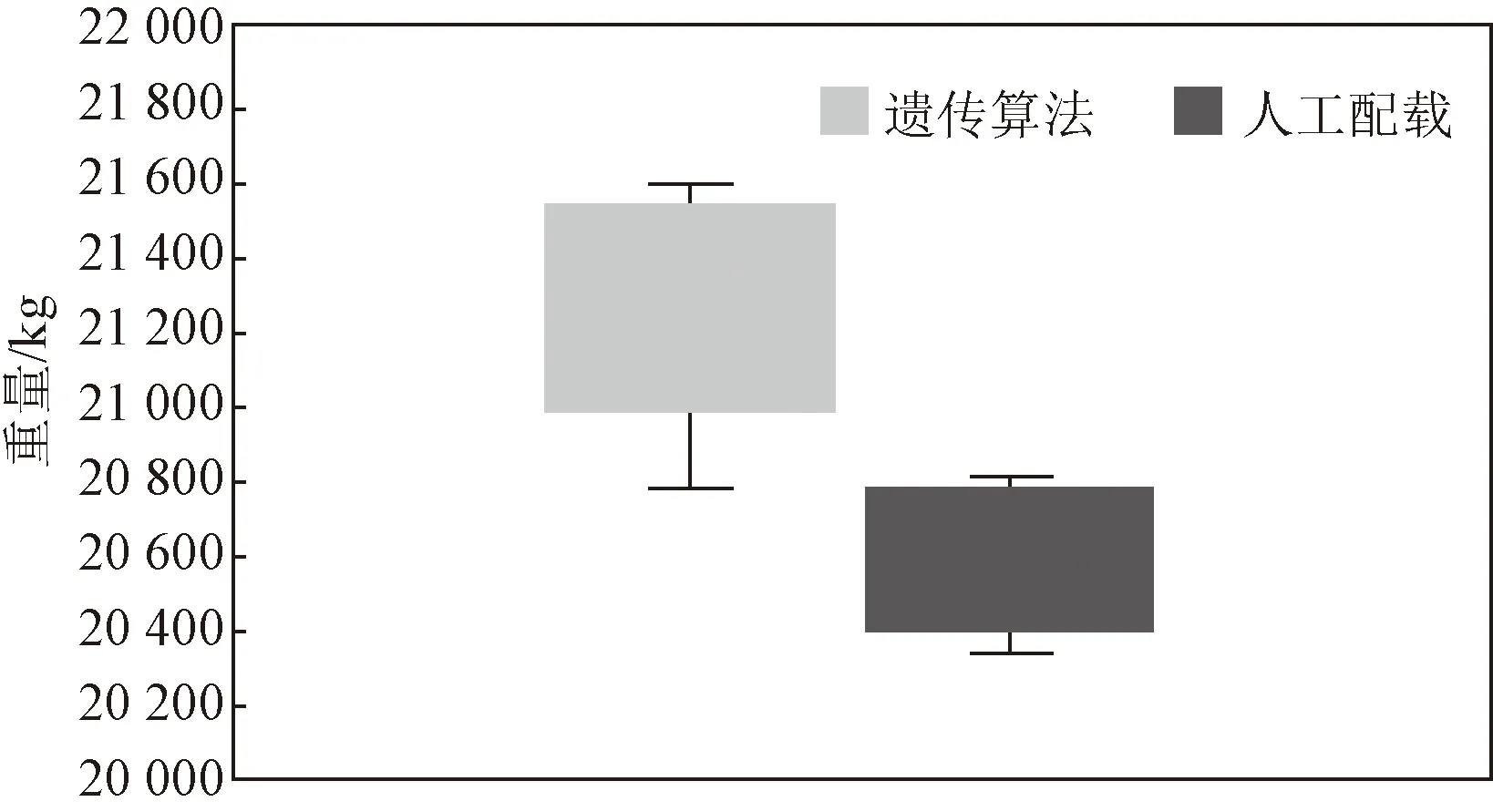
圖10 重量箱線圖Fig.10 Weight box diagram

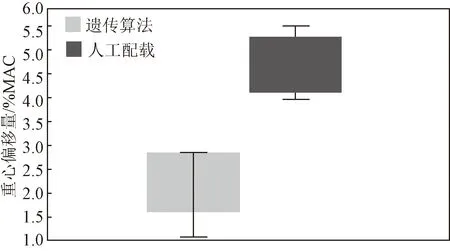
圖11 重心偏移箱線圖Fig.11 Boxplot of center of gravity deviation

4.3 多目標權重分析

為驗證算法的有效性，擬多次調整多目標權重的取值。表5為在不同ω1下所計算得到的業載及重心，為保證數據的有效性，同一ω1下計算10組取均值得到。

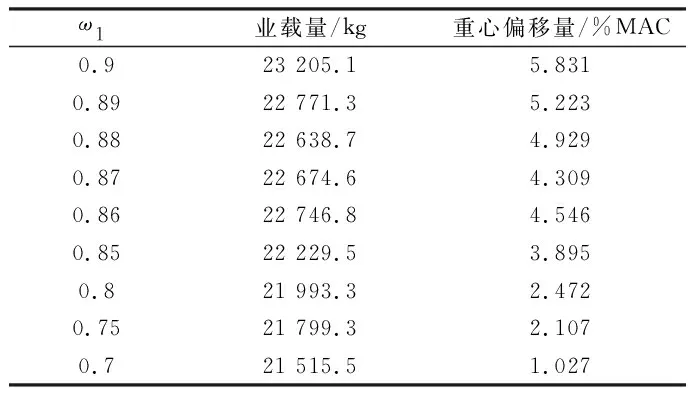
表5 不同ω1下的業載及重心偏差Table 5 Payload and center of gravity deviation under different ω1

在每個權重下計算多次得到圖12的業載量和重心偏移量變化曲線，隨著權重ω1的減小，業載量呈降低的趨勢；在ω1從0.9減小到0.67過程中，重心偏移量呈接近目標重心的趨勢。因此在實際情況下，各航司可以根據需要來選取不同的權重ω1滿足需求。

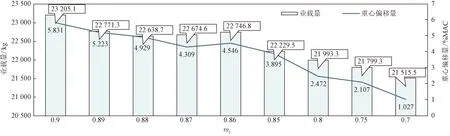
圖12 不同ω1下的業載及重心偏差Fig.12 Payload and CG deviation under different ω1

5 結論

載重平衡工作在地面保障工作中發揮了重大作用。針對航空公司目前所存在的問題，如何獲得一個可行的裝載優化方案，建立了民航飛機貨艙載重平衡模型，并運用改進的遺傳算法進行求解。對B757-200F進行實例計算結果顯示，平均業載可達21 281 kg，平均偏移量為2.31%MAC。由于所選機型為窄體機，在今后的研究工作中可以考慮寬體機的載重平衡問題，同時在重心優化上可以考慮將重心包線作為目標函數，來避免使用重心偏移量作為目標函數使得飛機重心偶然超出重心范圍。