考慮換乘接續的高速鐵路網末班車時段列車運行調整研究
溫鵬程,趙 鵬,姚向明,2,張 璞
(1.北京交通大學 交通運輸學院, 北京 100044;2.北京交通大學 智慧高鐵系統前沿科學中心, 北京 100044)
我國高速鐵路(以下簡稱“高鐵”)成網運營,旅客出行換乘較為普遍,2020年我國高鐵旅客發送量為21.67億人次,換乘客流量為3.4億人次,占15.7%,大型樞紐站換乘客流占比可達20%~30%[1]。列車運行受到干擾可能引起本線列車延誤并導致旅客無法換乘至其他線路。高鐵夜間檢修,末班車往往是旅客完成當日行程的最后機會,若銜接失敗將導致換乘旅客無法到達目的地,對旅客出行造成嚴重影響。落實以人為本的理念,合理制定適用于末班車時段的調整策略以提高換乘接續水平及整體可達性,是行車調度調整需考慮的現實問題。
列車運行調整是軌道交通領域的熱點問題,大多數學者以列車為中心,研究常規時段列車運行的快速恢復,降低損失。文獻[2-3]對線路故障導致區間能力完全失效與部分失效場景下的列車運行調整問題展開研究,將列車運行過程抽象為“事件-活動網絡”,建立混合整數線性規劃調整模型。在此基礎上,文獻[4]考慮動車組接續問題,拓展運行調整問題的研究范圍。文獻[5]以車站及線路通過能力為約束,建立以列車取消數量及總晚點時間最小為目標的整數規劃模型,并考慮終到站的正點率對結果的影響。文獻[6]研究模型的計算效率問題,基于約束規劃方法建立優化模型及算法,顯著縮短求解時間,但優化效果不及既有求解方法。文獻[7]研究區間限速場景下的列車運行調整問題,將列車延誤時間與數量轉化為滿意度,建立線性及梯形滿意度加權模型,提供新的建模思路。文獻[8]權衡晚點對旅客及列車的影響,提出適當放寬列車延誤要求以滿足更多旅客出行需求的調整思路。文獻[9]通過加入空駛列車及旅客繞行其他線路的方式來滿足中斷發生后的旅客出行需求,證明該策略能有效降低旅客損失。文獻[10]考慮列車延誤對鐵路管理者、調度人員及旅客的影響,建立旅客行為仿真模型模擬其出行過程,以運營成本、列車正點率、旅客出行時間為目標構建模型。文獻[11-12]將列車靈活停站、靈活折返與傳統策略結合,提出一種中斷場景下的實時調整模型。文獻[13]研究路網多處中斷場景下的調整問題。末班車運行調整方面,城市軌道交通領域已展開初步研究。文獻[14]構建地鐵網絡末班車時刻表調整模型,采用ε約束法求解。文獻[15]以最大化OD對可達性為目標建立混合整數規劃模型并基于Dijkstra算法求解。文獻[16]將地鐵網絡末班車時刻表協同優化問題轉化為時空網絡,采用拉格朗日算法求解。綜上,國內既有研究較少從旅客出行角度展開,國外雖有部分研究考慮到旅客但并不適于我國;對于末班車的調整在城市軌道交通領域已逐步受到重視,但其與高鐵運營特點存在較大差異,研究成果不適于高鐵。我國高鐵具有運輸距離遠、運行時間長、末班車時間跨度大等特點,旅客乘車實名制、票席對應,調度部門能夠實時獲取完備的旅客出行信息,為以客運服務為導向的列車運行調整創造了條件。因此,需要基于我國高鐵運輸組織特點及優勢,研究適合我國高鐵末班車時段的運行調整方法。
本文重點考慮列車延誤對旅客換乘的影響,緊密結合高鐵特點及末班車時段旅客出行需求,以實際客票數據與列車運行圖為基礎,研究末班車時段列車運行調整及旅客換乘調整問題。基于末班車時段旅客出行需求的特殊性,提出采用調整接續列車出發時刻、旅客靈活換乘車次、列車靈活停站、列車小幅度超員策略與變更列車區間運行/停站時間、調整列車運行次序等策略結合的調整方案,建立線性整數規劃模型,并通過案例分析驗證模型的有效性。
1 問題描述
線路末班車是指一條線路運行的最后一班列車。末班車時段指研究范圍內的路網上各線路末班車中始發時刻最早的一列末班車的始發時刻至所有列車運行結束時刻為止的時段。本文以路網上某一換乘樞紐站為中心,考慮末班車時段內所有從該站發出或到達該站的列車,以換乘旅客為研究重點,將旅客換乘前、后乘坐的2列列車分別定義為前續列車和接續列車。
末班車時段考慮旅客換乘接續的調整策略見圖1,線路1上有A、B、C等車站,線路2上有C、D、E等車站,換乘旅客從線路1出發前往車站D、E,需在車站C進行一次換乘。G3與G13是2條線路的末班車,末班車時段為該路網上各線路末班車中始發最早的末班車(即G3)始發時刻至所有列車運行結束(即G13終到)時刻為止的時段,車站C為換乘樞紐站,該時段內有2列列車到達C站,2列列車從C站發出,其中G1與G3為前續列車,G11與G13為接續列車。共6名換乘旅客,其中2名“白色旅客”目的地為D站(乘坐G1與G11),4名“黑色旅客”目的地為E站(2名乘坐G1與G11,2名乘坐G3與G13),原始列車運行見圖1(a)。
若前續列車發生延誤,G1到達C站時與G11之間的接續時間無法滿足換乘時間要求,將造成原計劃換乘G11的4名旅客滯留在C站,無法完成出行,故障時列車運行見圖1(b)。為減少換乘失敗的旅客數量,提高旅客的可達性,可采取利于旅客換乘的調整策略,如“調整接續列車出發時間”,當G1晚點時適當推遲接續列車G11在C站的出發時刻,使二者接續時間滿足換乘時間要求,則旅客可成功換乘,列車靈活停站且超員見圖1(c)。此外,還可以針對旅客進行調整,如“旅客靈活換乘車次”,當旅客錯過計劃換乘的接續列車G11時,可靈活換乘至后續列車G13。但G11與G13停站方案不同,后者在D站并無計劃停站,2名“白色旅客”換乘G13后仍無法到達目的地,此時可采取“列車靈活停站”的策略,使G13在D站增加臨時停站以送達2名“白色旅客”。由于原計劃換乘G11的4名旅客改為換乘G13,因此需考慮列車容量的限制,必要時可采取“列車小幅度超員”策略,盡可能使更多旅客成功到達目的地,接續列車始發等待見圖1(d)。當然,這樣調整可能會增加列車總晚點時間,影響列車運行效率,因此,需根據實際情況在換乘失敗的旅客人數及列車總晚點時間兩目標間進行權衡。
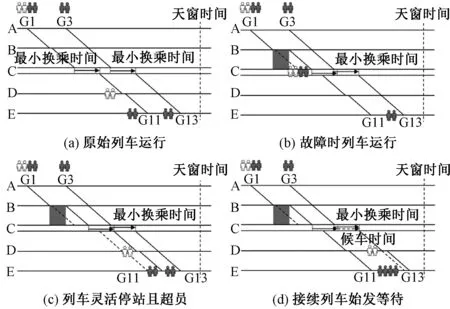
圖1 末班車時段考慮旅客換乘接續的調整策略
如果接續列車延誤,前續列車與接續列車間實際接續時間仍滿足要求,旅客可以成功換乘,因此不考慮這種情況。本文主要研究前續列車發生延誤時,如何通過合理的行車調度及旅客換乘調整措施,盡可能使更多旅客成功到達目的地。
2 末班車時段列車運行調整模型
2.1 假設及符號說明
為便于研究,假設如下:
(1)不考慮旅客換乘其他交通方式、改變出行線路等行為,所有旅客服從鐵路工作人員安排,對于直達旅客的時間損失,通過列車晚點時間間接表明。
(2)不考慮備用車和動車組運用問題。
(3)各車站上下行方向線路分別獨立,不同方向列車進出站及運行互不干擾。
(4)故障發生時若已駛入故障區間的列車尚未通過,需等待至故障排除方可繼續通行。
(5)末班車調整不可占用天窗時間。
L為線路集合,l為某一條線路,l∈L;S為車站集合,s為某一車站,s∈S;V為列車集合,i、j為列車,i,j∈V;Sl為線路l上車站的集合;Vl為線路l上列車的集合;M為一個很大的數。相關參數及變量定義見表1、表2。

表1 參數符號及說明

表2 變量符號及說明
2.2 模型構建
既有的列車運行調整目標主要包括晚點時間最小、與計劃運行圖偏差最小、正點率最高等,從列車角度考慮無法準確反映客運服務質量。對旅客而言,發生延誤后能否成功完成出行才是其最關心的問題,特別是末班車時段內,即使延長在車站等待時間、改變乘坐的接續列車、或在列車容量有限時改變座位類型等,只要能成功到達目的地,都可以接受。本文綜合考慮換乘旅客與列車兩方面因素建立雙目標模型。目標Z1為最小化列車延誤導致換乘失敗的旅客人數,目標Z2為最小化列車總晚點時間,保證末班車時段客運服務質量的同時兼顧了列車運行效率。
minZ1=
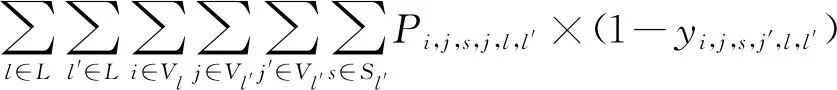
( 1 )
( 2 )
根據旅客和列車在實際運行中的限制及規則,建立約束。
(1)旅客換乘相關約束
為保證旅客成功換乘并順利到達目的地,前續列車與接續列車接續時間需滿足換乘走行時間要求;且接續列車需在旅客目的地停站;有多列接續列車滿足要求時,旅客僅能換乘其中1列。換乘約束為
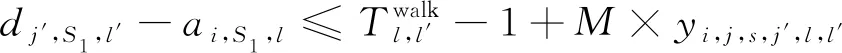
?i∈Vlj,j′∈Vl′s∈Sl′l,l′∈L
( 3 )
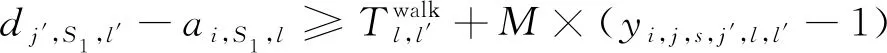
?i∈Vlj,j′∈Vl′s∈Sl′l,l′∈L
( 4 )
yi,j,s,j′,l,l′≤d′j′,s,l′?i∈Vlj,j′∈Vl′s∈Sl′l,l′∈L
( 5 )
( 6 )
列車載客人數應滿足容量約束
Pi,j,s,j′,l,l′+C′j′,l′?j′∈Vl′l,l′∈L
( 7 )
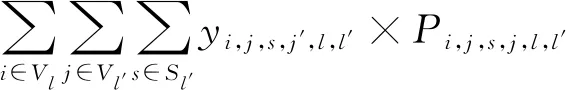
(2)運行調整基本約束
突發故障發生前,所有列車均按計劃運行;故障發生后,調度人員可調整列車到發時刻,但為滿足旅客基本乘車需求,調整后列車在任意車站的出發時刻均不能早于其計劃出發時刻。需滿足基本約束
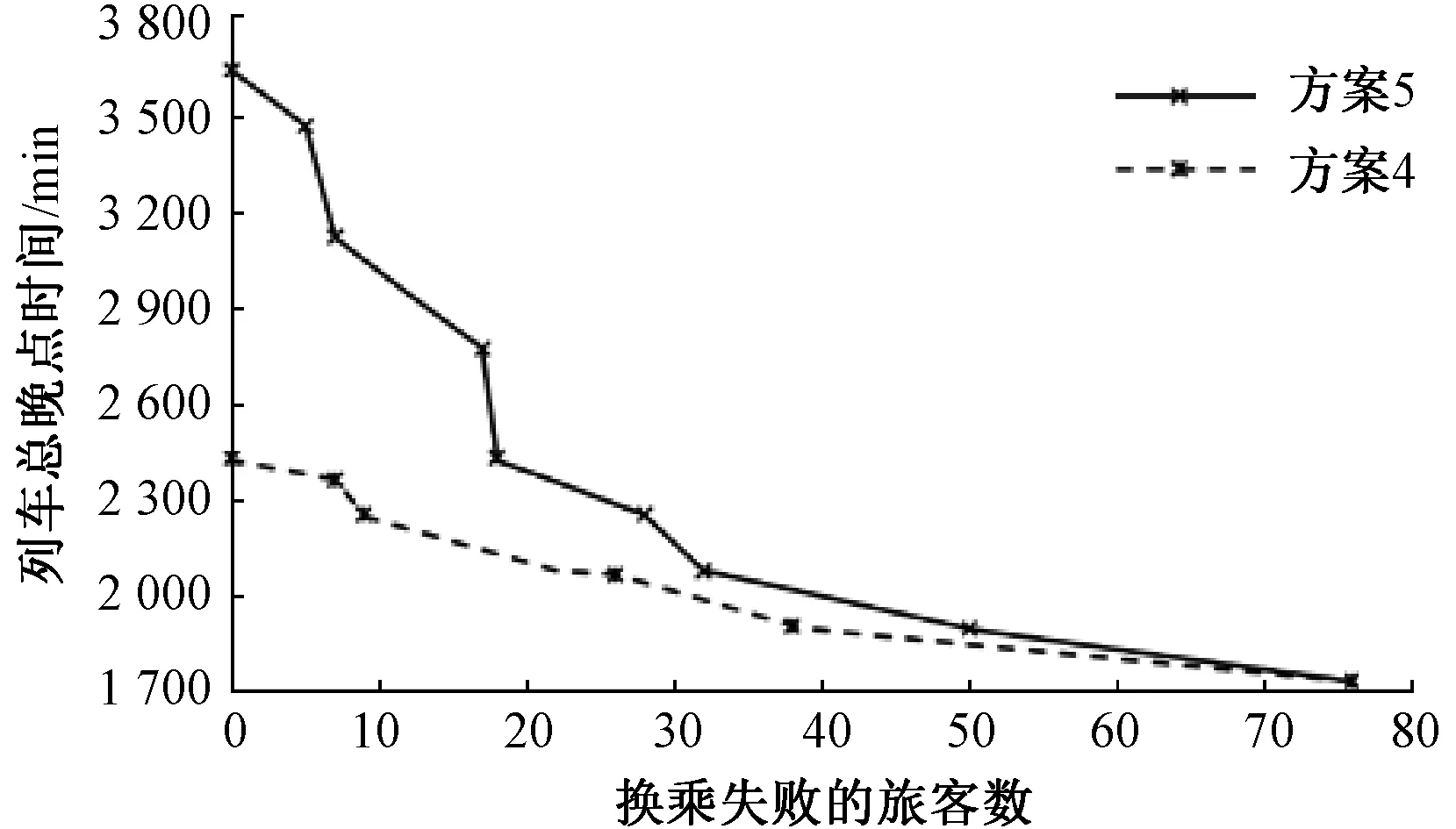
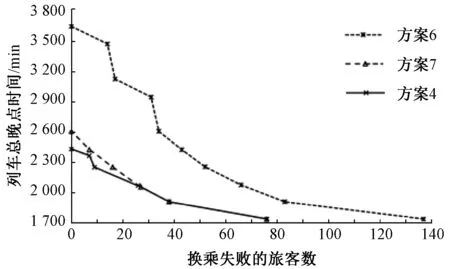
ai,s,l=Ai,s,l?i∈Vls∈Sll∈LAi,s,l ( 8 ) di,s,l≥Di,s,l?i∈Vls∈Sll∈L ( 9 ) 末班車時段內,應確保列車運行不占用天窗時間,以保證夜間檢修作業順利進行。天窗約束為 ai,s,l≤Tend?i∈Vls∈Sll∈L (10) (3)停站與運行時間約束 為保證旅客乘降作業順利進行,列車在原停站方案中計劃停靠的車站必須停站,未計劃停靠的車站可增加額外停站;對列車停站時間應予以限制,若停站則其在車站停留時間應不小于最小停站時間,若不停站則其在該站的實際到達時刻與實際出發時刻相等。停站約束為 d′i,s,l≥D′i,s,l?i∈Vls∈Sll∈L (11) ?i∈Vls∈Sll∈L (12) 列車運行過程中,在任意區間內運行時間應不小于最小純運行時間與起停附加時間之和,且不能大于最大純運行時間與起停附加時間之和。需滿足運行時間約束 ?i∈Vls∈Sll∈L (13) ?i∈Vls∈Sll∈L (14) (4)追蹤間隔與越行約束 為保證行車安全,同一線路上運行2列列車在同一車站的出發(到達)時刻需滿足最小追蹤間隔時間要求;調度人員可調整其運行次序,根據我國高鐵線路特征,列車只能在車站越行。需滿足追蹤間隔與越行約束 ?i∈Vlj∈Vls∈Sll∈L (15) ?i∈Vlj∈Vls∈Sll∈L (16) (17) (18) (19) (5)與突發故障相關的約束 受突發故障影響,列車無法在故障期間通過對應區間,需在前方車站待避至故障排除方可繼續通行。故障直接影響到的列車需滿足約束 ?i∈Vls∈Sll=L* (20) ?i∈Vls∈Sll=L* (21) ?i∈Vls∈Sll=L* (22) (23) 列車在車站停留需占用到發線,為確保故障發生區間前的所有車站s (6)到發間隔與車站能力約束 為保障列車安全運行與順利進出站,相鄰列車需滿足到發間隔約束 Hd≤ai,s,l-dj,s,l+M×(1-x′i,j,s,l) ?i,j∈Vls∈Sll∈L (25) 式中:x′i,j,s,l為0-1變量,i與j表示同一線路上的2列列車,s為i的到達站同時也是j的發車站,當x′i,j,s,l=1時,Hd≤ai,s,l-dj,s,l,列車j在車站s的發車時刻與列車i到達車站s的時刻滿足最小到發間隔要求Hd。 列車到達或通過車站需占用車站線路,式(24)可確保故障存在期間列車能夠在故障區間前方車站待避,但整個運行過程中應確保所有列車到達任意車站時都至少有1條線路可用,需滿足約束 ?i∈Vls∈Sll∈L (26) (7)有效不等式約束 列車i運行過程中,到達車站s的時間不可能既在故障發生前又在故障排除后;且若列車i在故障排除前從車站s出發,也一定在故障排除前到達車站s,相關事實已包含在其它約束中,但為了加快模型求解速度,求解復雜問題時可設置有效不等式約束 所建立的模型為雙目標線性整數規劃模型,可將其轉化為單目標進行求解。傳統的權重系數法存在需額外設置參數、統一量綱及權重分析等問題,為此,本文采用epsilon-約束方法轉化多目標模型并求得多組Pareto最優解集,分析采取不同方法調整時對目標的影響。模型目標包括換乘失敗的旅客人數最少Z1和列車總晚點時間最小Z2,其中旅客能否成功換乘是評價末班車時段內客運服務質量的關鍵因素,因此選取前者作為最終目標,將后者轉化為Epsilon-約束,求解步驟如下: Step2將目標Z2轉化為 (29) 式中:ε為對目標Z2的容忍度,0≤ε≤1。 并將式(29)加入到模型中,得到以換乘失敗旅客人數最少Z1為最終目標的單目標線性整數規劃模型。 Step3設置ε初始值為0,使用Cplex12.8對Step2所得模型編程求解,得到一組近似Pareto最優解。 Step4不斷更新ε取值(ε=ε+Δε,εmax=1),計算不同邊界條件下換乘失敗旅客人數最少的解,得到多組Pareto最優解集并完成求解過程。 選取西安北站為換乘樞紐站,路網范圍包括大西高鐵、西銀客運專線、西成客運專線及徐蘭高鐵鄭西段與蘭西段5條線路,西安北樞紐站銜接線路及站點分布見圖2。根據2021年9月某日的計劃運行圖,末班車時段起止時刻為19:36、23:54,該時段內到達換乘站或從換乘站發出的列車包括大西高鐵上下行12列、西銀客運專線上下行9列、西成客運專線上下行22列,徐蘭高鐵鄭西段上下行42列、徐蘭高鐵蘭西段上下行16列、共101列。需要說明,并非任意2列列車都存在接續關系,只有滿足換乘時間要求的一組列車間才有旅客換乘,案例中有換乘旅客乘坐的前續列車共38列,接續列車共13列。 根據實際客流數據,列車間換乘旅客人數小于20的占比達97%以上,接續時間短的列車間換乘人數多,接續時間超過200 min的無換乘旅客,為不影響結論的普適性,假設最小換乘時間15 min,換乘旅客人數以隨機數方式確定:①換乘等待時間不大于30 min的換乘量為10~20間的隨機整數;②換乘等待時間大于30 min的換乘量為1~10之間的隨機整數;得到總換乘人數1 863人。 列車起停附加時間分別取2、3 min,列車追蹤間隔、到發間隔取3 min,最小停站時間取2 min,天窗開始時刻為24:00,各車站到發線數量、列車在各區間最小純運行時間等參數均按線路實際設置,M取1 440。結合研究范圍內路網的基本情況,隨機生成5種故障場景,故障場景設置見表3。需要注意,部分早于末班車時段發生的故障也可能對末班車時段內的列車造成影響,這種情況也在研究范圍內。 表3 故障場景設置 上述模型在AMD R7-4800 H 3.2 GHz,內存16 GB的計算機上使用IBM Cplex Optimization Studio 12.8求解,所有場景均在200 s內得到最優解,滿足實際調度調整的實時性需求。為驗證模型有效性,設置不同調整方案調整目標及策略對比見表4。具體如下: 表4 不同調整方案調整目標及策略對比 方案1:故障導致列車運行延誤后不進行任何調整,列車仍按計劃的運行次序與停站方案運行。 方案2:以列車為中心的調整方法,目標為最小化列車總晚點時間,調整列車運行計劃。 方案3:考慮延誤對旅客換乘的影響,兼顧晚點時間與換乘失敗旅客人數兩目標,調整列車運行計劃。 方案4:按本文提出的方法與模型,既考慮列車運行調整,也考慮旅客換乘策略調整。 各場景下故障持續時間分別取10、20、30 min,通過不同方案調整,取Pareto解集中使換乘失敗旅客人數最少的解,詳細結果見表5。 由表5可以看出:①與未進行任何調整的方案1對比,方案2的換乘失敗旅客人數平均可減少9%,但在場景1故障持續20 min時,調整后換乘失敗旅客人數增加了36%,說明以列車為中心的調整方案不利于旅客的可達性,甚至導致更多旅客換乘失敗而降低客運服務質量。②方案3的換乘失敗旅客人數平均可減少85%,且在任意場景下都可有效減少這一指標,但調整后列車總晚點時間平均增大46%,說明方案3對列車運行質量影響較大。③方案4考慮列車與旅客兩方面因素,與方案1和方案2對比,可有效減少換乘失敗旅客人數,與方案3對比,在改善可達性的同時降低了對列車運行質量及直達旅客的影響,整體優化效果優于其他方案。 表5 各場景下采用不同調整方案結果對比 結果表明,通過多種策略結合的調整方案,可在末班車時段更好的保證換乘旅客出行需求并兼顧列車運行質量,證明了本文所提出方法的有效性。 3.2節結果分析表明,通過考慮旅客換乘的調整方案可有效提高客運服務質量,但旅客能否靈活換乘至其他列車并到達目的地,列車停站方案與列車容量是主要限制因素,因此提出“列車靈活停站”與“列車小幅度超員”策略,并設置對比方案(見表6)分析2種策略對結果的影響。以場景1為例,取故障持續時間為30 min,從ε=0開始不斷更新ε取值(εmax=1,Δε=0.1),得到各方案下Pareto最優解集。 表6 是否采取“列車靈活停治”及“小幅度超負”策略的方案對比 (1)列車靈活停站策略分析 方案4與方案5目標值隨ε取值變化見圖3。可以看出:①列車總晚點時間最小時,換乘失敗旅客人數最多,各方案結果相同。②隨ε取值增加,采取調整接續列車出發時間或增加停站的策略,可減少換乘失敗旅客人數,但會增加列車總晚點時間。③方案5列車總晚點時間增幅大于方案4,當全部旅客換乘成功時,方案5總晚點時間為最小值的210%,而方案4僅為最小值的140%,這是因為列車靈活停站后,可滿足更多旅客需求,從而減少推遲發車的列車數量。 圖3 方案4、方案5的Pareto解集 因此,實際運用過程中調度人員需根據需求進行權衡并選擇合適的Pareto最優解。考慮到末班車時段使旅客成功出行是最重要的目標,采取“接續列車靈活停站”的策略能在保證可達性的同時降低對列車總晚點時間的影響,或在較低晚點時間條件下盡可能減少換乘失敗的旅客人數,從而有效提升客運服務質量。 (2)列車小幅度超員運行策略分析 方案4、方案6、方案7目標值隨ε取值變化如圖4。可以看出:①同一故障場景下,采取不同方案時列車最小總晚點時間相同,換乘失敗旅客人數與方案中允許的最大超員幅度相關。②當全部旅客換乘成功時,方案6列車總晚點時間為最小值的210%,方案7與方案4為最小值的150%與140%,這是因為列車小幅度超員運行時其容量可滿足更多旅客需求,從而減少推遲發車及增加停站的列車數量。 圖4 方案4、方案6、方案7的Pareto解集 因此,列車小幅度超員運行是有效的優化調整策略,且允許的列車超員幅度越大,優化效果越明顯,調度人員在實際運輸生產過程中可在保證運行安全的前提下采取該策略進行調整,使更多旅客成功到達目的地并有效提高末班車時段的可達性。 兼顧列車和旅客的調整是軌道交通列車運行調整的必然方向,本文以末班車時段為背景進行了嘗試,得到一些有益的結論。 (1)提出調整接續列車出發時間、旅客靈活換乘車次、列車靈活停站、列車小幅度超員等多種策略結合的調整方案,從列車和換乘旅客兩方面出發,建立線性整數規劃模型。該模型實用性良好,可快速求得多組Pareto最優解集,為調度人員提供輔助決策。 (2)對比不同方案調整效果,證明多種策略結合的調整方案能有效減少換乘失敗旅客人數并兼顧列車運行質量。分析調整策略發現列車靈活停站與列車小幅度超員可方便旅客靈活換乘,提高方案調整效率。案例分析表明所提出的方法與模型能夠為末班車時段以客運服務為中心的列車運行調整方案制定提供理論基礎與方法支撐。 (3)主要研究調整方法,調整時會涉及旅客座位類型變更、車票改簽、退票等問題,列車延誤也將增加列車運行成本與旅客時間成本,若旅客換乘末班車失敗,還會帶來食宿成本等經濟損失,因此考慮列車及旅客廣義綜合成本等復雜經濟問題的運行調整是下一步研究重點。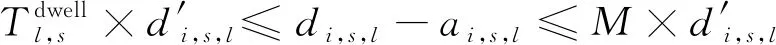
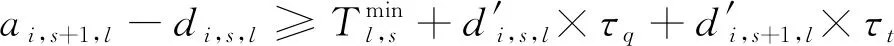
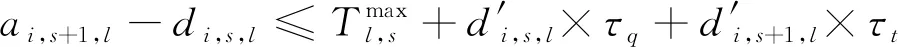
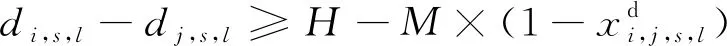

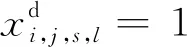
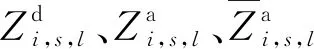
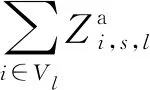
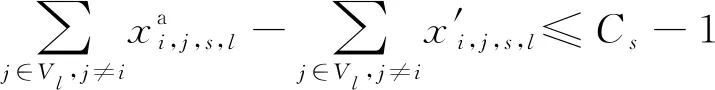
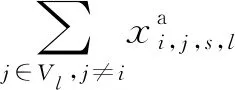
2.3 模型求解
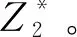
3 案例分析
3.1 基本信息

3.2 結果分析

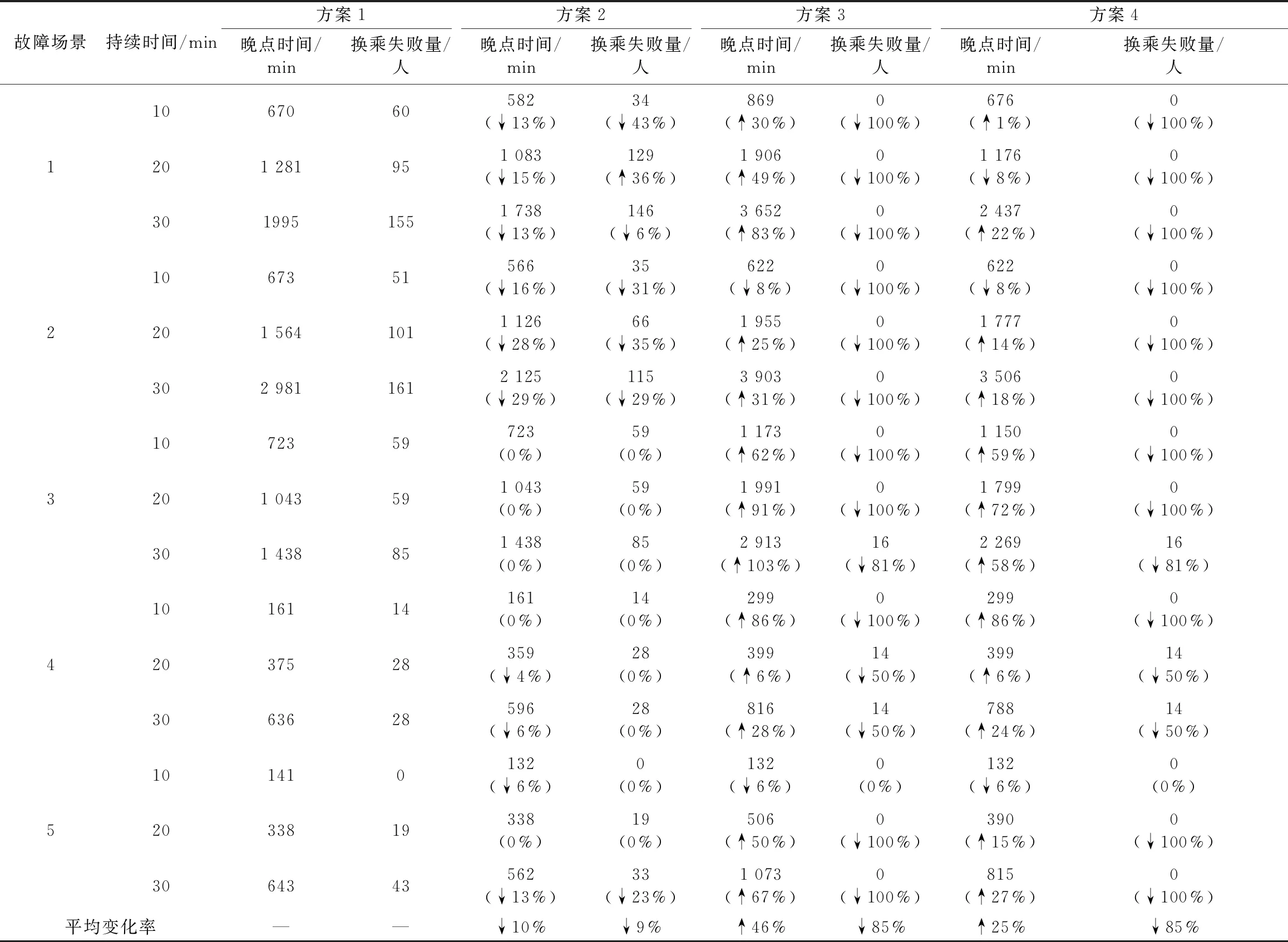
3.3 調整策略分析

4 結論

