基于累積前景理論的高速鐵路差異化定價與坐席分配聯合優化方法

秦 進，吳志君，楊 康，毛成輝，黎熙瓊，CHANTHAVONG Vanpadith

(1.中南大學 交通運輸工程學院，湖南 長沙 410075；2.軌道交通大數據湖南省重點實驗室，湖南 長沙 410075)

我國高速鐵路(以下簡稱“高鐵”)營業里程已近4萬 km，路網規模、運輸密度等均居世界首位。根據統計資料，2019年我國高鐵動車組發送旅客同比增長14.1%，至22.9億人次，占全路旅客發送量64.1%[1]，這表明高鐵已經成為我國鐵路旅客運輸的主力。但目前高鐵的市場化運營水平相對航空、汽運等仍比較落后，尤其是客票定價還未能充分考慮市場需求特征，無法實現客流的有效引導和調節，導致熱門車次供不應求和冷門車次供過于求的情況同時存在，造成一定程度上的高鐵運輸資源浪費，也降低了高鐵服務水平和企業收益。

差異化定價是指對具有可替代性的多個產品制定不同的價格，調節供需匹配關系，從而實現服務水平和企業收益最大化的一種商品銷售定價策略，如法國高鐵允許同一起訖點(Origin-Destination, OD)的列車根據旅行時間、發車時段以及服務水平等因素設置不同的價格。目前我國高鐵正進行市場化運營的改革探索，在票價方面，也開始有學者嘗試通過對高鐵列車實施差異化定價，以達到調節客流、提高列車上座率的目的。Van[2]根據邊際成本理論研究鐵路客運最優定價決策，建議鐵路在不同發車時段采取不同票價；尹少成[3]指出鐵路應借鑒航空領域市場化經營經驗，列車票價應隨發車時段、購票時間等因素波動；王燦燦等[4]提出應根據運輸淡旺季的客流峰值不同，進行季節性的差異化定價；文獻[5-8]基于列車屬性特征的不同，以平衡列車能力利用率和實現系統效益增收為目標，構建多列車差異化定價方法。

由于客票定價與坐席分配之間存在密切聯系[9]，因此將兩者進行聯合優化正成為當前的研究熱點。既有研究多基于隨機效用理論或期望效用理論，假設旅客完全理性，構建相應優化模型，如趙翔等[10-11]考慮隨機需求特征，分別構建單交通模式和多交通模式下的平行車次差異化票價票額綜合優化模型；宋文波等[12]提出固定需求環境下的多列車差異化票價和票額的綜合優化方法；Hu等[13]通過形式票價描述坐席分配策略，有效降低問題規模。但這些研究在描述旅客行為時往往忽略旅客出行特征的不同。

出行特征是旅客選擇行為的主要影響因素之一[14]，Espino等[15]指出忽略旅客出行特征不能準確描述旅客選擇行為，從而導致高估所得優化方案的效果。部分學者為解決這兩個問題做出了嘗試。Qin等[16]利用前景理論描述旅客的有限理性，但是由于前景理論自身局限性，模型適用范圍較小。文獻[10,17-18]也有意識地考慮旅客出行特征，但模型中對于出行特征的體現不夠全面，均只涉及部分內容。

綜上所述，在高鐵差異化定價的既有研究中，對于旅客決策行為的非完全理性和旅客出行特征均考慮較少。行為科學領域中的累積前景理論(Cumulative Prospect Theory, CPT)，在保留前景理論能夠刻畫有限理性的優點的同時，利用累積變形概率函數實現了理論大范圍適用和滿足一階隨機占優現象，因此在高鐵差異化定價問題中引入CPT更具優勢。從理論層面看，高鐵票價影響需求，坐席分配決定供給，將票價和坐席分配進行聯合優化，是充分考慮供需匹配關系。從實踐層面看，高鐵票價制定與坐席分配相互聯系不可分割，在定價問題中聯合優化坐席分配，可進一步提升客票總收益，同時也可在一定程度上，避免實際需求與坐席分配方案相差較大，從而給工作現場帶來大量臨時調整工作[9]。本文基于歷史客票數據分析旅客出行特征并進行旅客分類，利用CPT描述每類旅客出行選擇行為的有限理性，在此基礎上以客票總收益最大化為目標，提出彈性需求下高鐵差異化定價和坐席分配的聯合優化方法。

1 變量定義及問題分析

旅客根據高鐵票價、旅行時間、發車時刻等多個因素進行列車選擇，最終形成多列車多OD間的客流分布。差異化定價的目的，在于給高鐵列車制定有差別的票價，引導客流轉移，形成新的票價水平下的客流分布狀態，使得列車之間的客流需求更為均衡，提高運力資源的利用效率和總收益的增長。

客流需求規律是進行科學差異化定價的基礎[19]。為準確描述高鐵旅客客流需求規律，需要深入分析高鐵旅客的出行特征。旅客出行特征主要包括出行目的、出行距離、出行時間和出行費用[20]。這些因素的細微差異，都可能會影響具體旅客的出行選擇決策。因此對每位旅客個體進行單獨的選擇行為描述是無法實現的。本文根據上述因素對旅客出行行為的影響規律對旅客進行分類，在此基礎上刻畫每類旅客的選擇行為。

另外，相關研究表明，旅客在出行選擇過程中的有限認知能力和邏輯推理能力，使得其決策過程呈現出有限理性的特征[21]，例如，旅客的出行決策都存在參照點依賴，并更傾向于追求低概率的“高價值獲益”和避免低概率“高價值損失”，同時旅客對損失的規避程度和對相同程度獲益的偏好程度也并不相同，但都厭惡損失[22-23]。

CPT是Tversky等[24]提出的描述性決策理論，認為有限理性的自然人是極大累積前景效用的追求者，累積前景效用是所有可能情形下價值函數值與累積概率值的乘積之和，價值函數與累積概率函數均是實際結果和決策人內心參照點偏離程度的函數。CPT理論主要貢獻在于將參照點作為價值曲線原點來體現參照點依賴，利用不對稱性的價值曲線反應厭惡損失，采用累積變形的概率函數解釋人追求小概率事件的心理，利用CPT可以較好解釋人在決策過程中的有限理性。因此本文根據客票數據對高鐵旅客進行分類，基于CPT理論進行不同類旅客的出行選擇行為的有限理性特征刻畫。

本文研究的問題可以描述為：針對給定的高鐵線路，首先根據旅客出行特征進行旅客市場細分，并準確刻畫各類旅客出行行為的有限理性選擇特征，在此基礎上構造科學的高鐵旅客彈性需求函數，以客票總收入最大化為目標，充分考慮列車運輸能力(坐席數量)、票價水平區間和票價不倒掛等約束，求解線路上服務各OD間的各高鐵列車的最優票價和和相應的最優席位分配數量。為簡化問題，做出以下合理假設：

(1) 列車開行方案已經給定且不發生變化。

(2) 按照旅客先到先得的規則服務，超出票額限制的出行需求將不被滿足。

(3) 旅客出行需求主要受票價、旅行時間、發車時刻和退票成本4個因素影響。

(4) 不考慮列車席位等級。

為方便后面描述，符號及定義見表1。

表1 符號及定義

2 旅客分類

出行特征是旅客選擇行為的主要影響因素之一，不同出行特征的旅客選擇行為呈現一定的差異[14]。本文依據出行特征對旅客進行分類，將出行特征類似的旅客歸為一類，為后續彈性需求函數的構建奠定基礎。高鐵的歷史客票數據包含著大量旅客行為信息，可以直觀反應旅客的旅行時間、出行距離和出行費用，盡管出行目的在客票數據中無法直接體現，但旅客的出行日期和提前購票天數可以從側面和局部反映旅客的出行目的。因此，本文考慮從歷史高鐵客票數據中選取出行日期、提前購票天數、旅行時間、出行距離、出行費用5個外顯變量，利用潛在類別模型實現考慮旅客出行特征的旅客分類。

潛在類別模型是一種將潛在變量理論和分類相結合的統計分析技術，利用最少的潛在類數目解釋外顯變量之間的聯系。既有研究多利用潛在類別模型對給定高鐵線路所有OD服務的所有旅客同時分類，僅能處理小規模數據，在客票數據超過5萬條時分類效果難以滿足要求[25]。此外由于客票數據中僅包含高鐵的出行費用和旅行時間，而目前高鐵出行費用和旅行時間都與出行距離密切相關，因此對所有旅客同時分類的方式，會忽略距離相近但備選交通方式集不同的OD間出行費用、旅行時間的差異，從而不能準確反映旅客出行特征。以京滬高鐵為例，濟南西—南京南和北京南—南京南的距離相差不大，但濟南西—南京南無直達航班，組合出行費時又昂貴，因此絕大多數旅客都會選擇高鐵出行，因此該OD間旅客備選交通方式主要為公路和鐵路。而北京南—南京南之間有直達航班，備選交通方式有公路、鐵路及航空。這兩個OD間旅客的備選交通方式的旅行時間集合、出行費用集合顯然有較大差異，在旅客類別細分時必須加以考慮。

本文以歷史客票數據為基礎，對每個OD間的旅客進行單獨分類。因為對于同一OD間的旅客，其出行距離相同，可選交通方式相同，所以旅客備選交通方式的旅行時間集合與出行費用集合組成是相同的。在后續旅客選擇行為描述中，通過不同的參數取值即可體現各OD間旅行時間、出行距離和出行費用不同給旅客帶來的影響，因此這3個外顯變量在旅客分類過程中不予考慮。再利用剩余出行日期A、提前購票天數B兩個能夠從側面反應出行目的的外顯變量，對每個OD間的旅客進行單獨分類以區分出行目的，即可實現在模型中全面考慮出行特征的主要內容。對每個OD間的旅客分類，也是對歷史客票數據的降維，可以處理更大量級的數據。

選取好外顯變量之后，提取的數據并不能直接用于分類，需要對所有外顯變量數據進行處理，以不同的數字表示各外顯變量的不同取值。借鑒文獻[25]思想及高鐵退票費率，分別對出行日期和提前購票天數分段進行適當調整。分水平處理結果見表2。

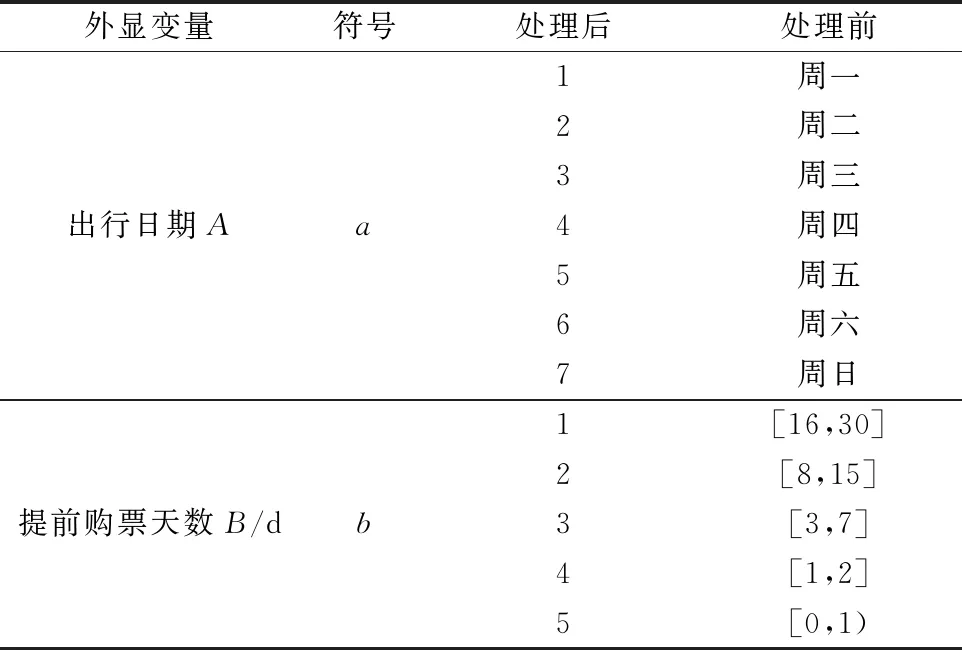
表2 分水平處理結果

根據潛在類別模型框架[25]，對于外顯變量組合為{a,b}的旅客，屬于潛在類別i的分類效用值Uabi為

a=1,2,…,7b=1,2,…,5

( 1 )

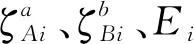
( 2 )

外顯變量組合為{a,b}的旅客屬于潛在類別i的概率P(i|{a,b})為

( 3 )

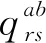
( 4 )

( 5 )

( 6 )

3 彈性需求函數構建

考慮到高鐵網絡中任意列車票價的變化，會影響系統內所有客流需求的時空分布，進一步又會影響多趟相關列車的需求分擔比例。因此不宜單獨確定單趟列車需求與其票價之間的彈性關系[10]。考慮到OD間的總需求與不同列車需求之間的內生關系，可以分2步確定列車的彈性需求函數，首先構建任意OD間的各類旅客總需求的彈性函數，然后建立服務該OD間所有列車的各類旅客需求分擔比例函數，對各類需求求和即可獲得不同列車的客流需求量。使用累積前景效用描述旅客出行行為的關鍵，在于構建出行效用函數和參照點。

根據累積前景理論，旅客是極大累積前景效用的追求者。累積前景效用的計算與高鐵出行效用、旅客內心參照點相關。累積前景效用的計算過程見圖1。

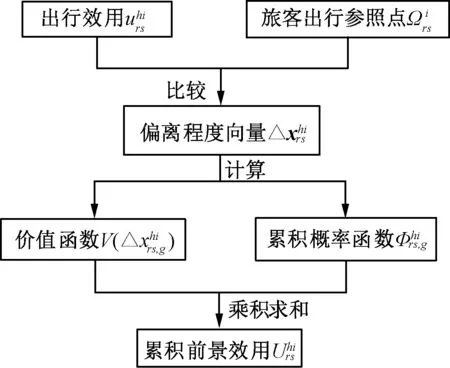
圖1 累積前景效用計算過程

(1)高鐵出行效用函數

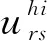
( 7 )

( 8 )

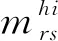
( 9 )

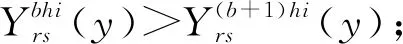
考慮現實中旅客對于出行效用微小差異的辨別能力十分有限，可利用離散分布擬合效用的連續分布[21]。舍棄高鐵出行效用連續分布兩側的小概率極端取值，保留一定置信水平y%下中間的置信區間。然后將置信區間等距分割成K份，認為該等距分割段的中值與該段其余值僅存在微小差異，可以取中值代表該等距分割段，作為高鐵出行效用波動的一個結果。由此，得到高鐵出行效用向量表達為

(10)

每一等距分割段上的概率分布值作為相應波動結果出現的概率，得到概率向量為P=(P1,…,PK)。

(2)出行決策參照點

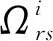
(11)

s.t.

(12)

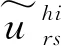
(13)

(3)高鐵出行需求彈性函數

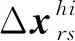
(14)

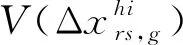
1≤g≤K

(15)

式中：α、β(0<α≤1,0<β≤1)用于判斷遠離參考點的敏感性變化，α、β的值越大，出行者對風險的感知越強；λ為損失規避系數，且始終存在λ>1，體現了決策者對損失的敏感性更強。

累積概率函數是描述旅客對客觀風險概率的反應程度，用參數δ反應累積概率函數的曲率。旅客的累積概率φ(P)為

(16)

(17)

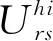
(18)

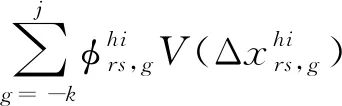
(19)

(20)

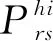
(21)

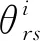
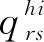
(22)

對所有類旅客求和，即可得到列車h的價格彈性需求函數為

(23)

4 聯合優化模型

以期望總客票收益最大化為目標，構建高鐵差異化定價與坐席分配聯合優化為

(24)

s.t.

(25)

m∈[1,N-1]h∈Hrs

(26)

(27)

(28)

(29)

h∈Hrs

(30)

(31)

h∈Hrs

(32)

模型中，式(7)體現了根據旅行時間、發車時段等不同因素對列車差異化定價的影響，由差異化價格調節需求；式(24)、式(25)體現了差異化定價和坐席分配的聯合優化；式(26)為列車運輸能力約束；式(27)為票價上下限約束；式(28)、式(29)表示對于同一到站或同一發站，較長區段的票價應高于較短區段的票價，避免產生票價倒掛現象；式(30)表示長區段票價應不小于其他可以拼接成該區段的各較短區段的票價之和，避免旅客多段拼接購票或者“買短+上車補票”；式(31)表示坐席分配取值下限，τ為最小滿足客流需求比例，避免一味追求最大利益而致使某些OD不分配坐席數量；式(32)表示決策變量的取值范圍。

5 模型求解

5.1 基于多段映射罰函數的模型轉化

模型中式(28)～式(30)是有關票價的關鍵約束，為求解算法設計帶來了困難。可以采用非固定多段映射罰函數對其進行轉化處理，以避免罰函數法中難以確定罰因子難題[30]。

構造廣義目標函數為

(33)

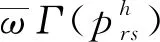
懲罰力度與懲罰項的更新公式為

(34)

(35)

(36)

(37)

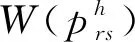
上述聯合優化模型屬于混合整數非線性規劃，并且票價和預期售票數量組合維度大，基于CPT構造的彈性需求函數含有正態分布和多次非線性變化，一般優化算法難以在有效時間內求取高質量的最優解。基本灰狼算法(Grey Wolf Optimizer, GWO)是一種全新的群智能優化算法，通過模擬狼群狩獵行為實現優化，由于全局搜索能力強、調整參數少等優點，在工程領域應用廣泛[31-32]。本文結合所研究問題的特征，在對基本灰狼算法進行改進的基礎上，設計求解方法進行計算與分析。

5.2 GWO算法基本思路

GWO算法的基本原理，是狼群中每一只狼位置信息代表問題的一個解，最容易捕獲的獵物位置代表優化問題的最優解，狼群逐漸靠近獵物實施抓捕，即不斷優化獲得最終解的過程[31]。首先通過隨機的方式，在可行域范圍內隨機生成初始狼群位置，對每一個體灰狼位置進行適應度值計算。根據適應度值將狼群劃分為4個等級，狼群中位置最優個體、次優個體、次次優個體分別記為記為G1、G2、G3，其余灰狼均為低等級狼G‘。

在迭代過程中，G1、G2和G3被認為是3只高等級狼，擁有獲取獵物位置的潛在能力，高等級狼共同指導所有低等級灰狼G‘進行位置移動。捕食過程前期，狼群離開當前獵物位置前往別處搜尋更容易捕獲的獵物，即進行全局搜索；到了后期，狼群逐漸靠近當前獵物實施抓捕，進行局部搜索。

算法執行中通過線性變化的距離控制參數d來影響狼群采取何種行動。狼群位置每更新一次，重新計算適應度值，根據適應度值更新高等級狼的位置，新的高等級狼繼續指導狼群移動，循環往復，直至捕獵行為結束。當算法迭代結束時，G1狼的位置代表優化問題的最終解。

5.3 GWO算法的改進

GWO存在以下幾處不足：首先，初始狼群位置隨機生成，狼群位置分布并不總是均勻的，而既有研究已證明初始種群均勻分布能提升群智能算法的尋優能力[33]；其次，線性變化的距離控制參數d并不能始終很好地平衡算法全局搜索能力和局部搜索能力；最后，算法中缺乏陷入局部最優后的跳出機制。針對上述不足，對GWO算法進行改進。

(1)初始狼群的改進

利用佳點集策略生成均勻分布的初始狼群。任意給定一定數量的點，用這些點的函數值構成的任何加權求和形式來近似計算函數在歐式空間單位立方體上的積分時，所取得的誤差最小的點集稱為佳點集。佳點集本質上是一個均勻分布的點集。將歐式空間單位立方體上的佳點集映射到求解空間能夠使初始狼群在解空間中均勻分布。記問題決策變量維數是Dim，取Q個點的佳點集Dn(m)用以狼群初始化。

Dn(m)={({exp(1)×m},{exp(2)×m},…,

{exp(Dim)×m}),m=1,2,…,Q}

(38)

式中：{exp(·)×m}為exp(·)×m的小數部分。Dn(m)佳點集的每個分量均在[0,1]之間，為了將單位立方體上的佳點映射至解空間，還需要將佳點集進行映射處理。映射f為

f[exp(g)×m]=lbg+{exp(g)×m}×(ubg-lbg)

(39)

式中：lbg、ubg分別為第g個分量的取值上下限。對佳點集Dn(m)中每個佳點的每個分量執行映射f，即得初始狼群。基于此方法構造的初始狼群隱含票價上下限約束，能保證票價在上下限范圍內均勻取值。

(2)距離控制參數的改進

灰狼算法中距離控制參數d的設置，影響著算法全局搜索能力和局部搜索能力的平衡。可以考慮使參數d非線性遞減以提升算法性能，即在迭代的前期，選擇較大的d值可提高全局搜索能力以避免算法出現早熟收斂的情況；迭代后期，有較小的d值可以讓狼群在某區域內集中搜索，加強局部搜索能力。

(40)

式中：iter和itermax分別為當前迭代次數和最大允許迭代次數。

(3)最差位置改變策略

基本灰狼算法沒有考慮陷入局部最優之后的跳出策略，因此本文借鑒隨機蛙跳算法[34]對適應度最差蛙的位置改變策略對灰狼位置更新方式進行改進。在每一次迭代過程中，計算每個灰狼個體對應的適應度值，記錄最差適應度值的灰狼個體。引入蛙跳概率Pfrog，在每次迭代過程中生成隨機數和Pfrog的值進行比對。當隨機數大于Pfrog時，最差灰狼個體按基本灰狼算法更新位置；當隨機數小于等于Pfrog時，最差灰狼個體按照式(41)更新自身位置，即最差灰狼個體跳出當前解，根據最優灰狼位置去尋找更優解。

(41)

5.4 算法步驟

具體算法步驟如下：

Step1根據給定線路，從歷史售票數據中獲取列車開行方案、固定票價下客流量等數據。設置模型和算法所需的參數。

Step2初始化算法迭代參數。當前最優適應度值Fmax=-∞，迭代次數iter=0，3只高等級狼G1、G2和G3的位置向量設為零向量。

Step3初始化狼群。根據佳點集理論初始化灰狼種群，每一只灰狼的位置向量對應一組票價集合。

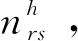
Step5G1、G2和G3適應度值及位置向量更新。將當前代灰狼種群的適應度值與G1、G2和G3的適應度值進行比較，更新G1、G2和G3適應度值以及對應的位置向量。

Step6狼群位置更新。根據式(40)計算距離控制參數，更新灰狼位置向量；同時按照蛙跳概率Pfrog更新最差灰狼位置使其能跳出局部最優。

Step7判斷算法是否滿足收斂條件。如果是則算法終止，輸出最優票價組合G1位置向量及其對應最優坐席分配方案，輸出最優客票收益值Gα對應的適應度值；否則返回Step4繼續迭代。

6 算例分析

以京滬高鐵下行(北京南往上海虹橋)的G1、G3、G5、G7、G11、G13、G15、G17共8列車為研究對象進行計算分析。當前運行圖中各列車的停站方案見圖2。為避開假期等特殊時期對客流的影響，選取2017年6月1日至30日作為數據統計時段，將每趟列車的日平均客流量作為算例的初始客流需求。

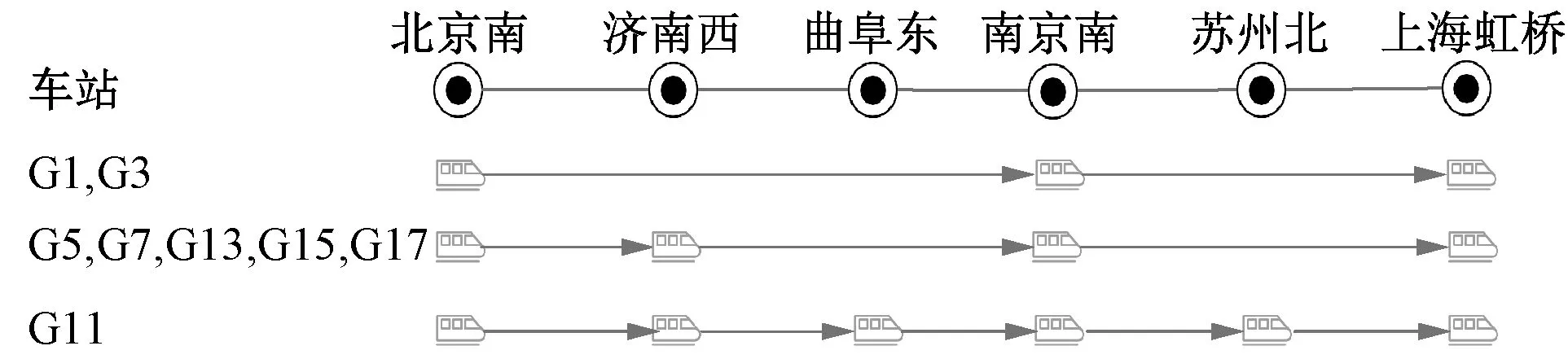
圖2 停站方案

6.1 旅客分類結果分析

為了便于求解和保證結果合理性，需要找出既具有較少類別，又具有較好擬合優度的旅客分類結果。進行擬合優度檢驗的主要方法有似然比卡方統計量檢驗G2、Pearson 檢驗χ2，基于似然比卡方檢驗的信號評價指標AIC和Bayesian信號評價指標BIC。這里將上述4種指標結合起來進行模型擬合優度的評價，指標越小表明模型適配度越高。利用Latent Gold軟件對潛在類模型進行求解，將潛在類別個數從1開始逐個增加至5，結合BIC、AIC、χ2、G24種評價選取最終潛在類別個數。以OD對北京南—上海虹橋為例，潛在類模型檢驗指標輸出見表3。隨著潛在類別個數的增加，指標χ2、G2一直下降；而BIC、AIC先下降后又升高，分別在潛在類別個數為4和5的時候達到最小值。當數據量較大時，BIC是主要參考指標，因此北京南—上海虹橋最佳潛在類別個數為4。

表3 北京南—上海虹橋潛在類模型檢驗指標

不同OD對之間達到最優擬合效果的潛在類別個數并不完全相同，算例中所有OD的最優潛在類別見表4。

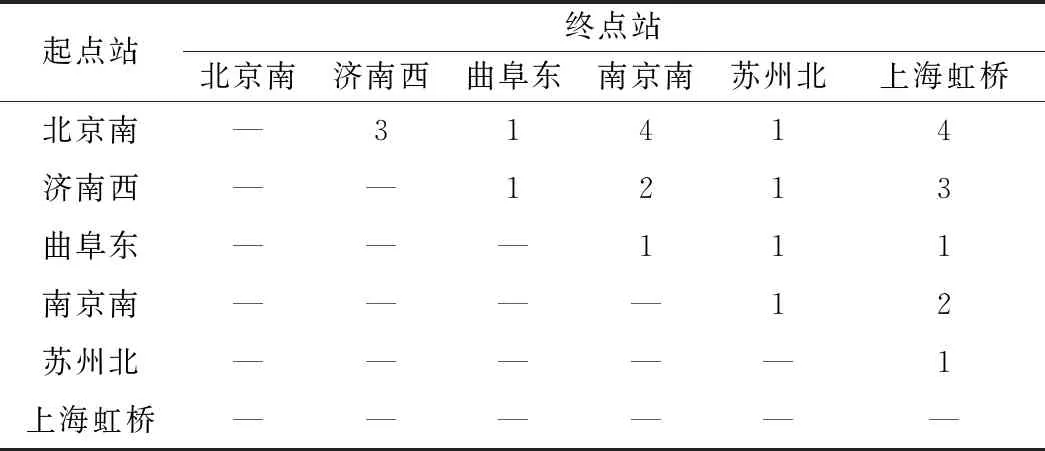
表4 各OD最優潛在類別數目

對于最優潛在類別為1的OD對，表明在算例研究范圍內該OD對的全體旅客出行特征都類似，不需要額外進行分類。對于其余OD對，考慮到多個潛在類別會增加聯合優化模型的求解復雜度，且模擬結果中這些OD潛在類別為2時BIC的值與最小值相差均不超過1%，故本文將這些OD旅客分為2類，即潛在類別數目為2。以濟南西—上海虹橋為例，潛在類別數目設置為2時，參數擬合結果見表5。

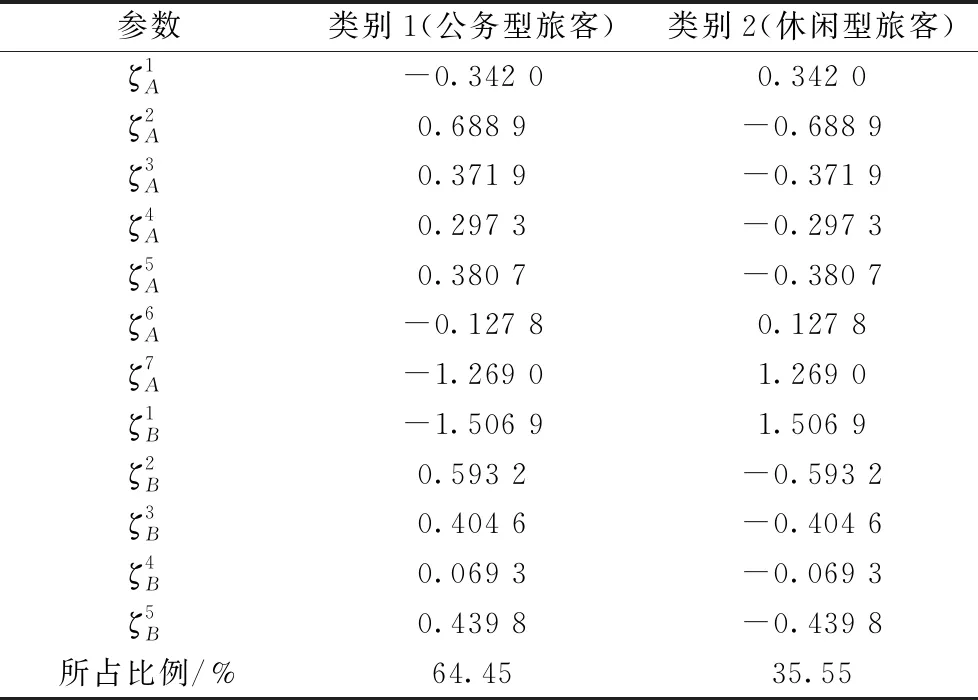
表5 濟南西—上海虹橋潛在類模型參數擬合結果

將2類旅客分別命名為公務型旅客和休閑型旅客。從參數擬合結果來看，該OD對旅客以類別1為主，占比達64.45%。類別1旅客的顯著特點是傾向于在工作日出行，一般較晚購票，計劃性較弱，此類旅客的出行目的偏向于公務出差，因此命名為公務型旅客；而類別2旅客傾向于周末出行，提前較長時間進行購票，計劃性較強，這些特征表明該類旅客出行目的偏向于休閑旅游，因此命名為休閑型旅客。

6.2 結果分析

所得的最優方案中，8趟列車的總客票收益為4 528 824元，較原始固定票價下的總客票收益(4 326 914.5)元增加了4.67%，優化后票價結果見表6。從表6可知，相對于初始票價，不同OD對的票價有不同的波動情況。北京南—上海虹橋運輸距離長，同時有直達航班，旅客需求彈性大，各列車通過降價的方式吸引更多旅客進行購票。而北京南—濟南西運輸距離超出了公路的優勢運距范圍，且沒有直達航班，旅客需求彈性較小，各列車票價上漲以達到提升收益的目的。值得注意的是，同一OD對各列車差異化定價結果，并不完全取決于該OD間初始客流需求的分布。以北京南—濟南西為例，G15初始客流需求僅為19人，但優化后票價上漲了18.16%。這是因為G15大量席位被分配給北京南—上海虹橋的旅客，僅有少量席位可供北京南—濟南西的旅客預定。因此G15在北京南—濟南西票價上漲，正是通過票價調節需求，使得旅客選擇其他高鐵列車。這從側面說明了高鐵差異化定價是一個復雜的組合優化問題，最終票價結果需綜合考慮所有OD需求在各列車之間的分布情況。

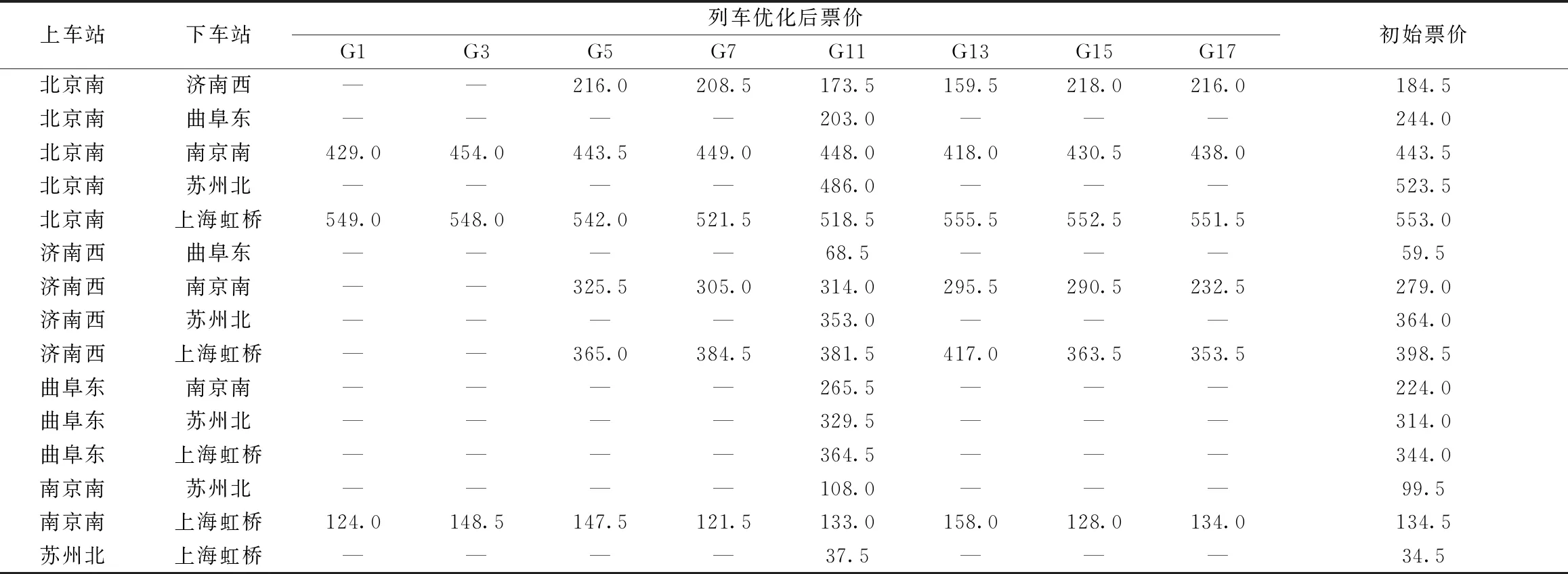
表6 優化后票價 元

將最大值與最小值之差與平均值的比值定義為差異值，用以衡量各列車優化后票價的差異大小。不同OD對不同列車之間優化后票價差異見表7。由表7可知，在具有多趟列車的6個OD對中，優化后的票價差異比較明顯，始終處于[5.83%,28.67%]。

表7 優化方案票價差異值情況 %

票價發生變化，各OD的客運需求也發生改變，因此各OD的票額分配數量也相應變化，最終實現列車發送旅客人數變化，各OD總客流變化情況見表8。由表8可知，在差異化定價方案下，總發送客流量呈現上升趨勢。從不同OD 來看，差異化定價方案下長途客流增加，短途客流減少。在采取單一票價時，由于費率采取遞遠遞減的梯度設置，在短途客流能完整裂解全程席位的情況下，分配短途票額能使收益達到最大化。但是在差異化定價條件下，單位費率并不一定符合遞遠遞減的梯度原則。并且短途初始票價不高，客流需求彈性系數也相對更小，同等比例的票價變化幅度對短途客流需求調節力度相對更弱，票價對客流的調節作用并不總能實現大量短途客流完整裂解全程席位。結合表6的票價優化結果，差異化定價方案傾向于以低票價吸引長途客流，以最大程度利用列車運輸能力，發揮高鐵運距長的優勢。

表8 各OD總客流量變化情況

差異化定價提升客票收益的關鍵在于提高列車能力利用率。票價優化前后，各區段列車客座率對比情況見表9。由表9可知，優化之后更多區段趨于飽和，部分車次在部分區間客座率有明顯提升。結合表7中各OD總客流量變化可知，長距離OD客流量增加足以彌補短距離OD客流量的部分減少，從而使得各區段客座率有不同程度提升，部分區段甚至所有列車的客座率均達到1。

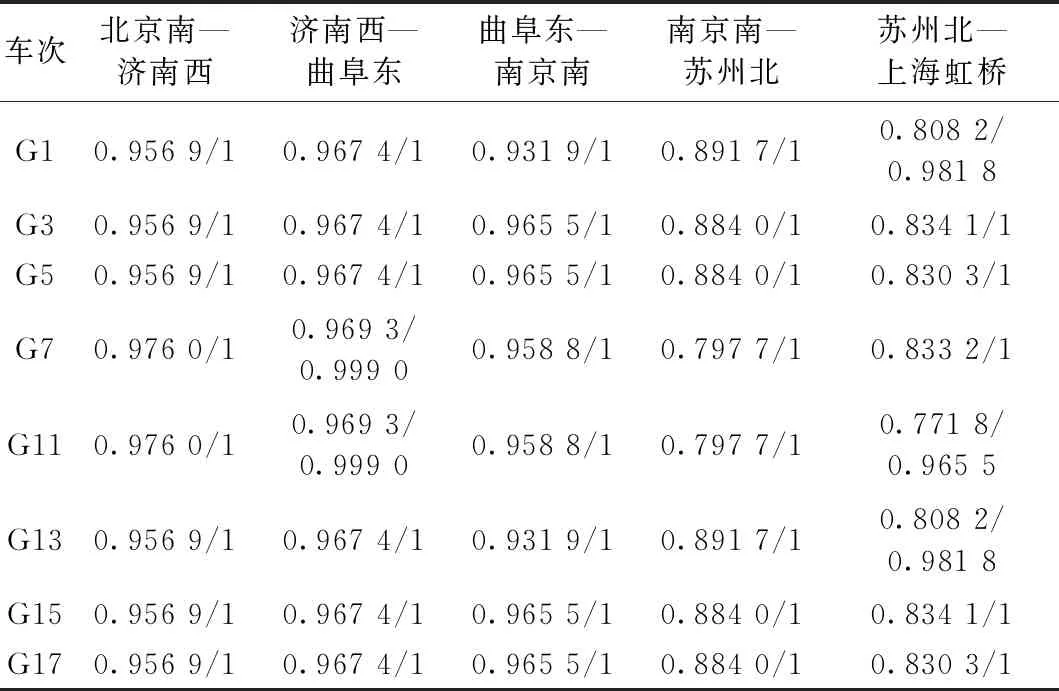
表9 不同列車不同區段客座率變化情況

各區段列車客座率的方差見圖3。由圖3可見，從列車客座率的方差角度來看，每個區段列車客座率方差均顯著減小，這說明不同列車客座率之間的差異減小，差異化定價充分發揮了客流調節作用，使得旅客在不同列車之間的分布更為平衡。

圖3 客座率方差

7 結論

固定票價無法有效調節高鐵客流，可替代列車之間客座率相差較大，造成運輸資源浪費，未能充分挖掘高鐵盈利能力。本文著眼于該實際問題，從不同高鐵列車之間的可替代性出發，對高速鐵路差異化定價進行了研究。首先，利用潛在類別模型對旅客進行分類。其次，引入CPT構建差異化定價下的彈性需求函數。之后，構建高鐵差異化定價和坐席分配的聯合優化模型，并設計改進的灰狼算法對模型進行求解。最后，通過數據實例驗證模型和算法的有效性。主要結論如下：

(1)與既有方法相比，本文考慮了出行特征不同給旅客選擇行為帶來的影響，體現了差異化定價背景下旅客決策的有限理性，從而使得構建的彈性需求函數更貼近真實情況，對于鐵路企業市場化改革更具借鑒意義。

(2)京滬高鐵算例的數值驗證結果顯示，本文方法所得各OD間各列車之間票價差異明顯，坐席分配方案科學合理。在不投入更多運輸資源的同時，差異化定價與坐席分配聯合優化可使企業客票收益上漲4.67%。本文研究成果能指導鐵路企業靈活定價和科學分配坐席數量，有助于提高服務水平，擴大收益，實現企業健康長足發展。

(3)高鐵差異化定價是復雜的組合優化問題，某OD間某列車的票價優化結果并不僅僅取決于該OD間初始客流需求，而是多OD間多列車共同作用的結果。因此，多OD間多列車定價問題研究更具意義。

(4) 差異化定價對客流有明顯調節作用。票價優化后，各OD間客流量產生明顯變化。長途旅客相較于短途旅客，彈性系數大、初始票價高，在運輸資源較為充裕的前提下，差異化定價方案更傾向于以低票價吸引更多長途旅客，從而提升客票收益。差異化定價方案有利于發揮高鐵在中長途運輸中的運距優勢。各列車區段客座率有明顯提升，多個區段能力趨于飽和。同時，各列車區段客座率方差顯著減小，說明差異化定價后旅客需求在不同列車之間分布更為均勻。