鈦合金葉片加工變形的迭代循環分析研究

方靜弦，曹 燕，2，程 寓，黃 雷

（1.南京理工大學機械工程學院，江蘇 南京 210094；2泰州職業技術學院機電學院，江蘇 泰州 225300）

1 引言

由于葉片弱剛度，變曲率等因素，航空發動機葉片仍然存在加工變形量較大、效率低、精度低和表面質量低等問題，葉片加工變形及其控制仍然是目前的研究熱點之一[1-2]。國內外學者對葉片的加工變形進行了一系列相關研究。文獻[3]通過AdvanEdge仿真并計算獲得了鋁合金銑削力模型，運用迭代算法研究了鋁合金薄壁葉片的單點變形情況。文獻[4]總結了一些鋁合金薄壁零件的切削加工變形的控制技術，并運用有限元分析切削加工導致的彈性變形，最后檢驗和優化了加工工藝設計方案。文獻[5]對鋁合金薄壁壁板類零件加工過程中瞬時變形量進行有限元仿真，并分析其變形規律，對于薄壁零件加工質量和變形控制等研究具有一定意義。文獻[6]通過有限元分析得到薄壁件在加工過程中的瞬時變形量及變形規律，建立了兩端自由、兩端固定的鋁合金薄壁件及葉輪葉片的有限元模型，得出結論：葉片的最大變形位于進氣邊處，最小變形位于葉尖處。文獻[7]運用ANSYS與MATLAB對葉片彈性變形量進行運算，實現了直紋面葉片加工變形的計算，并完成了變形結果的仿真。文獻[8]針對發動機葉片銑削加工變形，考慮由于加工變形、刀具變形及刀具偏心引起的瞬時切削厚度變化對銑削力模型中各系數的影響，通過有限元預測模型，將變形量補償到程序中，實現了葉片加工誤差的離線補償。文獻[9]先通過實驗獲得切削ZTC4鈦合金的切削力和刀具磨損的經驗公式，接著建立了有限元分析模型，利用生死單元法、移動載荷技術和刀具磨損量線性疊加方法，最終得到了該型薄壁件的加工變形規律。文獻[10]基于反變形思想，提出了葉片加工變形誤差的多次補償方法，并研究了誤差補償中的葉片補償模型重構和光順問題，最終結果表明通過該方法葉片加工精度得到了提高。

針對鈦合金葉片的銑削加工，考慮變形量和銑削力相互影響的情況，采用有限元以及迭代循環的方法，研究鈦合金葉片的銑削變形規律。為控制葉片的加工變形，提高加工精度，提供更為精準的依據。

2 鈦合金葉片變形研究

2.1 鈦合金葉片加工模型

鈦合金葉片的加工大致，如圖1所示。由于變形主要發生在精加工過程中，所以研究對象是精加工的鈦合金葉片，預先設定0.4mm的加工余量，采用點銑的銑削方式。圖中：刀具為簡化的半徑3mm的球頭銑刀，葉片總高度約為90mm，上下寬度各約30mm和50mm，厚度各位置不同，約為（2～3）mm，葉片整體具有一定曲率。將寬度方向命名為U向，由左到右為正向，高度方向命名為V向，由上到下為正向。裝夾方式采用葉片底端完全固定。

圖1 鈦合金葉片加工示意圖Fig.1 Machining Sketch of Titanium Alloy Blade

2.2 葉片彈性變形迭代循環分析

彈性變形產生“讓刀”，并且無法避免，導致實際切削深度和名義切削深度有所差異，從而使得實際變形量會發生變化；另一方面，在實際的銑削過程中，銑削力也會隨之變化，銑削力和彈性變形之間會相互作用，變形量會使得實際切削深度減小，從而銑削力會隨之減小，然而銑削力的減小會使變形量減小，從而使得軸向切削深度增大，從而銑削力增大……如此循環，如表1所示。最終達到某一平衡。

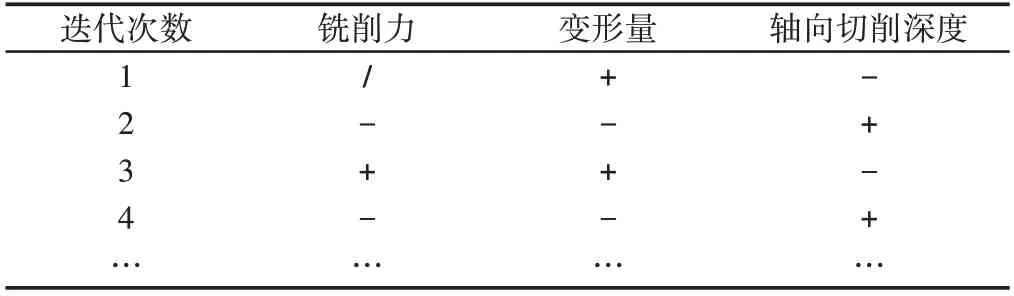
表1 迭代規律Tab.1 Iteration Rules

這里/表示還未變化的初始值，+表示增大，-表示減少。

軸向切削深度和變形量的迭代公式，如式（1）所示。

式中：ɑp(k)—第k次迭代計算得到的實際軸向切深；ɑp(0)—名義軸向切削深度；Δy(k)—第k次迭代計算獲得的在葉片曲面上某點法向變形量。

2.3 葉片加工變形有限元分析

2.3.1 有限元分析假設

由于鈦合金葉片的加工是一個很復雜、難以模擬的過程，并且會受到很多因素的影響，所以首先需要對有限元分析進行一系列的假設來簡化模型：

（1）假設球頭銑刀銑削加工時，葉片受到的銑削力為某一刀觸點上的集中力；

（2）忽略加工時余量的去除對于葉片剛度的影響；

（3）只考慮“讓刀”造成的工件彈性變形，不考慮由切削熱、殘余應力等因素造成的其他變形。

2.3.2 有限元設置

（1）邊界條件：葉片底面完全固定，精加工階段采用點銑的銑削方式。

（2）模型及材料屬性：將UG10.0建立的鈦合金葉片三維立體模型導入ANSYS19.0中，材料屬性等，如表2所示。

表2 材料屬性及單元類型Tab.2 Material Attributes and Element Types

（3）網格劃分：映射劃分，即將葉片表面劃分成長寬均勻的網格，這里單面葉片面上劃分成14*14的網格，沿U向V向各取7個均勻分布的節點施加載荷，并記錄下這些節點編號，以便后面進行變形研究，這樣兩個面上均有49個網格點。

（4）通過rotatenodecs的操作，將所有網格節點上施加載荷都設置為該點曲面法失方向。輸入想施加載荷的點標號，再輸入力的大小即可設置載荷。在230號節點處施加法向力，如圖2所示。

圖2 法向力的施加Fig.2 Normal Force Exertion

2.3.3 鈦合金葉片加工變形量的計算方法

（1）軸向銑削力和切削深度的迭代

由于在葉片的銑削加工過程中，變形主要是由軸向力導致的，所以使用通過鈦合金四因素-四水平正交銑削實驗得到的經驗公式，來表示軸向銑削力和各參數之間的關系。

將每次更新的切削深度作為變量，銑削力作為因變量，可以得到軸向銑削力和切削深度的迭代式（2）。

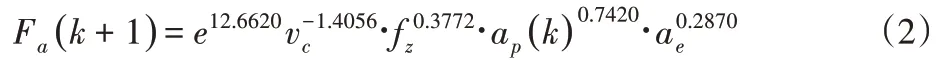
式中：Fɑ(k+1)—第k+1次迭代后的軸向銑削力；e—自然對數的底數；vc—切削速度；fz—每齒進給量；ɑp(k)—第k次迭代的軸向切深；ɑe—銑削寬度。

設定好初始參數，取參數，如表3所示。

表3 初始參數Tab.3 Initial Parameters

得出v c=94.2m/min

式中：d—球頭銑刀直徑，為6mm；n—轉速。

這樣通過式（2）可以求得初始軸向銑削力Fɑ(0)=58.1888N。

（2）變形量迭代流程

圖3 計算流程圖Fig.3 Flow Chart

其中ξ為預先設定的誤差極限。且迭代的次數設定為某一值ɑ，若超過此值迭代還沒有收斂，則停止計算并取ɑ次前的所有數據的平均值作為最終結果。取誤差極限ξ=0.05mm，ɑ=5。

（3）以某一點為例計算過程

計算刀軸矢量和該節點處曲面法矢的夾角，然后將初始軸向銑削力F0沿該點曲面法矢方向進行分解，在ANSYS上該點輸入值，再solve求解，最后用時間結果處理器獲得該點處曲面法矢方向上的變形量，為初始變形量Δy0，再通過圖2的計算流程，結合式（1）和式（3）進行迭代計算。該過程的計算量較大，可以使用MATLAB預先設定好軸向銑削力的計算公式，這樣每次只需得到更新的Δy，從而計算出更新的切削深度ɑp，輸入公式中即可得出新的銑削力，依此迭代，直到滿足誤差極限停止，得到該點的最終變形量。按照上述方法，將葉片一面所有49個點都進行求解。

2.4 變形量結果分析

（1）各節點處迭代循環前的變形量

（2）各節點處迭代循環后的變形量

以左上角銑削點為例，迭代后切削深度由初始的名義切削深度0.4mm變成了實際切削深度0.21mm，對比表4和表5可以看出，該點為最大變形點，迭代前初始變形量為249μm，迭代后該點最終變形量變為190μm，前后差距達到59μm。其他點的變形量經過迭代后也均發生變化，隨著初始變形量增大，前后差異也隨之增大。

表4 初始變形量（單位μm）Tab.4 Initial Deformation（μm）

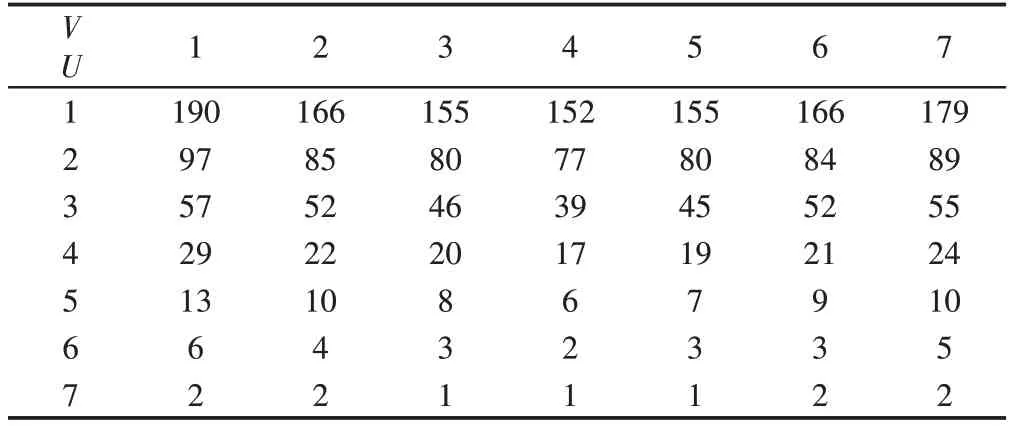
表5 迭代后變形量（單位μm）Tab.5 Deformation after Iteration（μm）

再通過MATLAB將這些點的變形量擬合，即可得到經過迭代循環分析后的鈦合金葉片加工變形預測結果圖。

3 結論

從數據和圖中大致可以看出：

（1）容易發現，由于約束的關系，葉片沿著U向正向，變形量先減小后增大，近似關于中間對稱；沿V向正向，變形量逐漸變小。

（2）在考慮了讓刀變形和銑削力之間的相互作用之后，實際變形量與初始變形量在每個銑削位置均存在差異，變形量最大處，迭代后變形量減少了59μm。使用迭代循環的方法計算變形量，可以為控制變形提供一個更為精準的依據。