基于二次回歸正交旋轉(zhuǎn)試驗熔融沉積超聲振動成型研究

何金輝，王海雄，劉善坤，李亞君

（桂林理工大學機械與控制工程學院，廣西 桂林 541004）

0 前言

FDM作為快速成型技術(shù)的一種，具有結(jié)構(gòu)簡單、材料成本低和后處理方便等特點，被廣泛應用于汽車內(nèi)飾、醫(yī)療衛(wèi)生和個性化工藝品制作等領(lǐng)域[1?2]。聚乳酸（PLA）材料由于具有良好的生物可降解性，成為FDM工藝中使用頻率最高的材料之一[3?6]。隨著對FDM的不斷研究，其應用領(lǐng)域越來越廣泛，人們對其產(chǎn)品質(zhì)量的要求也明顯提高，成型產(chǎn)品的力學性能和加工工藝之間的關(guān)系受到了許多研究人員的青睞，由于其加工工藝參數(shù)多而且內(nèi)部聯(lián)系機理較為復雜，因此通過優(yōu)化工藝參數(shù)來提高材料成型件的力學性能具有重要意義。

盡管FDM應用前景廣闊，但該技術(shù)的制造原理卻限制了FDM成型工件的力學性能上限。使其與有模制造注射成型零件相比具有因相鄰兩絲之間焊接不良而導致的強度不足等問題。為了提高FDM制品的力學性能，國內(nèi)外的研究人員普遍通過改進參數(shù)和材料改性的方式來實現(xiàn)。超聲波輔助加工技術(shù)作為一種新型的制造加工技術(shù)在許多行業(yè)應用廣泛。針對超聲波改善材料力學性能的問題，許多學者做了相關(guān)的研究，其中何智等[7]通過在電弧增材制造中增加超聲沖擊，使材料內(nèi)部柱狀晶粒的大小發(fā)生了改變，通過對比發(fā)現(xiàn)增加超聲振動后材料的拉伸強度有所提高。陳學永等[8]在激光燒結(jié)快速成型的過程中加入超聲波，使得材料內(nèi)部晶粒更加細化，硬度也明顯提高。Richard等[9]在研究納米晶表面改性時增加了超聲振動裝置，經(jīng)過超聲波處理后材料的表面粗糙度減小，硬度增加。通過以上研究發(fā)現(xiàn)超聲波在改善材料力學性能方面有很好的效果，因此本試驗在FDM的基礎上引入了超聲振動技術(shù)。在試驗方法上，朱晨穎、白鶴和文周等[10?12]一批研究人員分別使用了田口實驗法和正交試驗法對熔融沉積成型參數(shù)進行了優(yōu)化，這些方法雖然可以在試驗次數(shù)不多的情況下獲得較好的結(jié)果，但是不能在一定的試驗范圍內(nèi)根據(jù)數(shù)據(jù)樣本確定變量之間的相關(guān)關(guān)系以及相對應的回歸方程。二次回歸正交組合設計雖然能解決上述問題，但是依然存在二次回歸預測值的方差隨試驗點在因子空間的不同位置呈現(xiàn)出較大差異，由于存在誤差，因此很難由預測值找出最優(yōu)區(qū)域。而回歸正交組合的旋轉(zhuǎn)設計可利用具有旋轉(zhuǎn)性的回歸方程在進行預測時對于同一球面上的點可直接比較其預測值的好壞，克服了二次回歸正交組合設計的缺點[13]。

考慮到以上試驗設計中存在的不足，本文在原有成型方式上增加了超聲振動裝置，探究超聲振動對熔融沉積成型的影響。在此基礎上，分別選取外殼厚度、填充密度、超聲波功率3個因素為研究對象，采用二次回歸正交旋轉(zhuǎn)組合試驗法對熔融沉積成型工藝進行優(yōu)化，對提高熔融沉積成型制品的力學性能具有指導性的意義。

1 實驗部分

1.1 主要原料

本文使用的材料是ESUN品牌1.75 mm的PLA+3D FILAMENT熱塑性絲材，顏色為象牙白色；這種材料具有良好的熔體流動性和打印的平滑性；韌性高、硬度和剛度大、抗劃傷性能好、表面易于著色，被廣泛應用于FDM領(lǐng)域。

1.2 主要設備及儀器

熔融沉積成型3D打印機，Y7510，深圳巨影投資發(fā)展有限公司；

電子萬能試驗機，WDW?50，獻縣金晟試驗儀器廠；

超聲波電源（超聲波發(fā)生器），THD?T1，深圳太和達科技有限公司；

超聲波換能器，28KHZ60W，深圳旭升精密機械有限公司；

超聲振動FDM設備：在原有的FDM設備的成型基板上增加了超聲振動系統(tǒng)，通過調(diào)平裝置對設備進行了重新調(diào)平，使其能夠正常工作；組裝完成后的設備如圖1所示；超聲振動裝置主要由3部分組成，其中包括超聲波發(fā)生器、超聲波換能器以及輔助裝置；在工作中，超聲波換能器中特制的壓電陶瓷將超聲波電源產(chǎn)生的高頻電信號轉(zhuǎn)換為強有力的機械振動，最后通過輔助裝置把機械振動傳遞到成型基板上，從而實現(xiàn)超聲振動熔融沉積成型。

圖1 超聲振動FDM設備Fig.1 Ultrasonic vibration FDM equipment

1.3 樣品制備

根據(jù)GB/T 1040.2—2006中試樣的形狀與尺寸進行設計，采用的是1A型的啞鈴狀試樣[14]；FDM具體加工工藝過程如圖2所示，基本工藝流程可歸納為5步：

圖2 FDM工藝流程圖Fig.2 Flow chart of FDM process

（1）根據(jù)制造對象和設計要求利用三維繪圖軟件繪制符合尺寸要求零件的形狀并轉(zhuǎn)換為STL格式的文件。

（2）安裝材料，更換基座，進行分層切片處理加入支撐并檢查數(shù)據(jù)是否有誤，設置零件的成型位置和FDM成型的基本參數(shù)如打印溫度、噴嘴溫度、打印速度和超聲波功率等。

（3）對設備進行預熱，按照設置參數(shù)對零件進行逐層制造直至零件成型。

（4）可根據(jù)具體情況對已成型的零件進行后處理。

（5）若改變參數(shù)可重復步驟（2）、（3）、（4）進行。FDM樣品如圖3所示。

圖3 FDM樣品圖Fig.3 Diagram of FDM sample

1.4 單因素試驗設計

在FDM的過程中，有很多影響產(chǎn)品力學性能的因素，其中主要的影響因素有層厚、外殼厚度、填充密度、打印速度以及填充方式等。本試驗選擇同一種類的PLA+材料，在打印速度為60 mm/min、層厚為0.1 mm、打印溫度為220℃和填充方式為45°的條件下，研究外殼厚度（0.4、0.8、1.2、1.6 mm），填充密度（70%、80%、90%、100%）及超聲波作用功率（0、32、40、48、56 W）對FDM產(chǎn)品拉伸強度的影響。

1.5 二次回歸正交旋轉(zhuǎn)組合試驗設計

為了確定在多個因素下材料拉伸性能的最佳工藝參數(shù)，本文在單因素實驗的基礎上，選擇適當?shù)膮?shù)范圍，分別對外殼厚度（A）、填充密度（B）和超聲波功率（C）3個因素進行了二次回歸正交旋轉(zhuǎn)組合設計試驗，以拉伸強度（Y）為響應值，試驗變量因素水平如表1所示。

表1 正交旋轉(zhuǎn)試驗因素水平編碼表Tab.1 Factor level and coding of orthogonal rotation test

1.6 性能測試與結(jié)構(gòu)表征

為了排除各參數(shù)差異化對試驗造成的誤差，所有試驗采用同一個經(jīng)過改裝后的FDM超聲振動打印機。在測試過程中，保持恒定的拉伸速度不變，始終控制在3 mm/min，拉伸樣件的標距為50 mm。利用電子萬能試驗機對拉伸樣件施加縱向的拉伸載荷，可測得每個試樣的拉伸強度[15]。為了避免試驗的偶然性誤差，每組試驗數(shù)據(jù)測量3次，最終的拉伸強度取三者的平均值作為試驗值。

2 結(jié)果與討論

2.1 單因素實驗結(jié)果分析

為了研究不同外殼厚度對PLA制件拉伸強度的影響，選擇填充密度為90%，超聲波功率為40 W，結(jié)果如圖4所示。由圖可知，隨著外殼厚度的增加，拉伸強度也顯著提高。在外殼厚度小于1.2 mm時增長較快，但當外殼厚度為1.6 mm時，拉伸強度增長趨勢變緩。外殼厚度指平行于拉伸受力方向且與內(nèi)部填充物成45°夾角的壁厚。拉伸的過程中外壁往往會先出現(xiàn)斷裂而后內(nèi)部填充物才發(fā)生斷裂，在內(nèi)部填充物不變的情況下，隨著外殼厚度的增加，拉斷外壁的力也隨著增大，從而使拉伸強度不斷提高。當外殼厚度超過1.2 mm以后，在拉伸過程中整個零件內(nèi)外部受力較為均勻，外殼厚度對零件拉伸強度的影響逐漸減小，因此當外殼厚度大于1.2 mm時拉伸強度的增長趨勢會變緩。故本試驗選擇最適當?shù)耐鈿ず穸葹?.2 mm。

圖4 外殼厚度對拉伸強度的影響Fig.4 Effect of shell thickness on tensile strength

為了研究不同填充密度對PLA制件拉伸強度的影響，選擇外殼厚度為1.2 mm，超聲波功率為40 W，如圖5所示，隨著填充密度的增加，拉伸強度明顯提高，當填充密度在80%～90%之間時提高拉伸強度的效果最為顯著。其原因是：當填充密度較小時，噴嘴在走絲的過程中相鄰兩絲之間的空隙較大，缺乏有效支撐，內(nèi)部容易形成空洞的現(xiàn)象，因而導致填充密度小時，拉伸強度也較低。隨著填充密度的增加，相鄰兩絲之間的間隙也隨之減小，使零件更加致密，從而拉伸強度提升較快，特別是在填充密度為80%～90%之間時較為明顯。當填充密度超過90%時，兩絲之間是幾乎完全接觸但還沒有達到完全接觸的狀態(tài)，因此拉伸強度也有所提升但是提升速度相對變緩。由于試驗需考慮成本和效率，故選擇最佳的填充密度為90%。

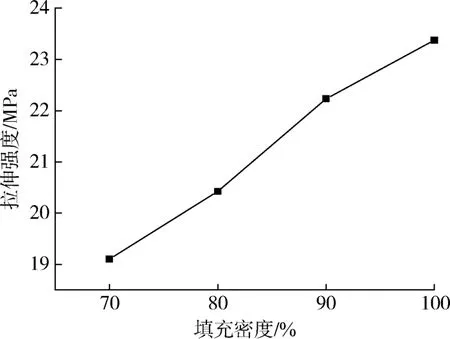
圖5 填充密度對拉伸強度的影響Fig.5 Effect of packing density on tensile strengt

為了考察不同超聲波功率對拉伸強度的影響，選擇外殼厚度為1.2 mm，填充密度為80%，由圖6可知隨著功率的增大，拉伸強度逐漸提高，當功率為48 W時拉伸強度最大，之后隨著功率的增加拉伸強度降低。其原因是，當超聲波功率在0～32 W之間時振動較小，外加能量損失嚴重，傳遞到工件上的振動較弱，因此拉伸強度增長緩慢。隨著超聲波功率的增大，振動逐漸增強，在超聲場的作用下，兩結(jié)合面處的分子鏈迅速穿過相鄰界面并產(chǎn)生聯(lián)結(jié)，同時高頻振動還會使一部分分子鏈斷裂，釋放出熱量，使熔體的黏度降低，增強了流動性，從而拉伸強度提升明顯。當超聲波功率超過48 W時，已突破了超聲波作用的界限，破壞了結(jié)合面處分子鏈的關(guān)系，同時也使工件的尺寸發(fā)生變化，因此拉伸強度出現(xiàn)了下降的趨勢。故選擇最佳超聲波功率為48 W。

圖6 超聲波功率對拉伸強度的影響Fig.6 Effect of ultrasonic power on tensile strength

在圖6中選擇了超聲波功率為0、32、40、48、56 W 5個變量進行試驗，其中每個變量中又選擇了3個平行樣進行測試，把3次測量的拉伸強度的平均值作為該變量下的拉伸強度，經(jīng)過計算分別得出5個變量下每個變量的偏差范圍，其結(jié)果如下：在0 W時最大偏差為2.55%，最小偏差為1.53%；在32 W時最大偏差為4.52%，最小偏差為3.12%；在40 W時最大偏差為1.25%，最小偏差為1.05%；在48 W時的最大偏差為2.15%，最小偏差為1.5%；在56 W時的最大偏差為3.72%，最小偏差為2.54%。由以上實驗數(shù)據(jù)的偏差范圍可知，最大偏差為4.52%，均小于5%，說明此次實驗測量結(jié)果在合理的范圍之內(nèi)。

2.2 二次回歸正交旋轉(zhuǎn)組合設計試驗結(jié)果及分析

根據(jù)單因素實驗結(jié)果，選取外殼厚度（A）、填充密度（B）和超聲波功率（C）3個因素，以拉伸強度（Y）為響應值，試驗方案及結(jié)果如表2所示。

表2 二次正交旋轉(zhuǎn)試驗方案及試驗結(jié)果Tab.2 Quadratic orthogonal rotation test scheme and test results

利用Design?Expert 8.0軟件對表2中的試驗數(shù)據(jù)進行分析，建立A、B和C三因素的回歸模型，計算得出回歸系數(shù)，得到拉伸強度（Y）的回歸擬合方程如式（1）所示：

對以上二次回歸方程進行方差分析，結(jié)果如表3所示。回歸模型的P=0.000 5，遠小于0.01，模型影響差異極為顯著。失擬項P=0.182 6>0.05，失擬項不顯著，說明預測值與試驗值之間有較強的相關(guān)性，擬合方程預測值和試驗值誤差比較小，可以用該擬合方程預測拉伸試驗的優(yōu)化工藝條件。模型的F值與拉伸強度成正比，F(xiàn)值越大則對拉伸強度的影響越大[16]。從各因素的P值大小可以判斷出A、B、C、外殼厚度和填充密度的交互項（AB）的P值均小于0.01，則說明其對拉伸強度具有極其顯著的影響。其余各項P值大于0.05則影響不顯著。從回歸方程的系數(shù)和表3中F值可以得出影響拉伸強度的因素由高至低的順序為：A>B>C。

表3 回歸模型方差分析Tab.3 Analysis of variance of regression model

利用Design?Expert 8.0軟件對上述回歸方程作3D響應曲面圖，如圖7所示，響應面可以反映因素之間的影響程度[17]，曲面越陡說明其對拉伸強度的影響越大。其中圖7（d）中隨著填充密度和外殼厚度的增加，拉伸強度先劇烈增加隨后又出現(xiàn)小幅度下降的趨勢，通過圖7（a）二維等高線可知，兩因素之間的交互作用明顯。如圖7（e）所示，隨著外殼厚度和超聲波功率的增加，拉伸強度逐漸增加，通過圖7（b）二維等高線可知，兩因素之間存在一定的交互作用。如圖7（f）所示，隨著填充密度和超聲波功率的增加，拉伸強度增加緩慢，通過圖7（c）二維等高線可知兩因素之間的交互作用不太明顯。此分析與方差分析基本吻合。

圖7 各因素對拉伸強度的等高線和響應面圖Fig.7 Contour and response surface diagram of various factors on tensile strength

2.3 驗證試驗

為了進一步驗證二次回歸模型的可靠性，任意選擇3種不同試驗方案的試樣進行驗證，每組中選擇3個樣本進行試驗，結(jié)果取拉伸強度的平均值。具體試驗結(jié)果和工藝參數(shù)見表4。從試驗結(jié)果可以得出，隨機選擇3組不同參數(shù)的試樣的拉伸強度分別為 22.253、22.232、22.316 MPa，通過二次回歸方程計算預測的拉伸強度分別為22.182、22.640、22.050 MPa，試驗結(jié)果與預測值誤差在0.3%～1.8%之間，誤差數(shù)值很小，表明試驗與回歸模型具有很高的重復性，因此回歸模型可靠。

表4 驗證試驗Tab.4 Verification test

3 結(jié)論

（1）在原有FDM設備上增加超聲振動裝置，通過試驗發(fā)現(xiàn)增加超聲振動后材料的拉伸性能比沒有增加超振動材料的拉伸性能有所提高；在同等的條件下，不加超聲波的平均拉伸強度為19.663 MPa，超聲波為40 W時的平均拉伸強度為22.38 MPa，加超聲波后對材料的拉伸性能提升了13.8%；為后續(xù)改善FDM產(chǎn)品的力學性能提供了一定的參考；

（2）通過試驗建立了外殼厚度、填充密度和超聲波功率3種影響因素和拉伸強度為響應值的相互作用模型，確定了最佳工藝參數(shù)組合為：外殼厚度1.2 mm、填充密度為90%、超聲波功率為40 W；此條件下的拉伸強度為22.05 MPa；

（3）通過響應面和等高線圖可以得到外殼厚度、填充密度、超聲波功率以及外殼厚度與填充密度之間的交互作用對拉伸強度的影響最顯著；影響拉伸強度的因素由高至低的順序為：A>B>C；采用二次回歸正交旋轉(zhuǎn)組合試驗進行回歸分析，擬合得到了拉伸強度和打印參數(shù)之間的數(shù)學回歸方程并且通過試驗對方程的可靠性進行驗證，結(jié)果表明二次回歸方程具有較高的重復性，可靠性良好。