基于深度強化學習的NOMA系統功率分配

劉樹培

(南京郵電大學通信與信息工程學院，江蘇 南京 210003)

1 概述

非正交多址(NOMA:Non-orthogonal multiple access)是一種有著廣泛應用前景的技術。NOMA的基本思想是讓多個用戶復用同一頻帶資源，主動引入干擾信息，在接收端使用串行干擾刪除(SIC：Successive interference cancelation)實現正確解調。具有高容量、低延遲、支持大規模連接等技術特點。在對NOMA系統的研究中，資源分配問題是其中的重要一環。資源管理策略包括功率控制、信道分配、用戶聚類、用戶調度、速率控制等。通過適當的資源管理和利用功率域中的用戶多樣性，可以協調NOMA用戶之間的干擾，從而提升NOMA網絡的性能[1]。

在文獻[2]中，作者針對NOMA下行鏈路的場景，在考慮用戶服務質量和最大發射功率的前提下，研究了子信道分配和功率分配問題。文獻[3]研究了上行鏈路NOMA網絡的接入時延最小化問題。作者將其分為2個子問題，即用戶調度問題和功率控制問題，并提出了一種迭代算法來解決該問題。在文獻和文獻中，作者將子信道分配和功率分配聯合考慮，但這種聯合資源分配問題通常是NP-hard的，采用傳統方法優化很難得到最優解。

由于傳統方法依賴于對系統的建模，且計算復雜度較高。而機器學習在解決這些復雜的數學問題時表現出了巨大的優勢。強化學習(RL: Reinforcement learning)作為機器學習的一個主要分支，可以作為實時決策任務的選項之一。在NOMA系統中，強化學習算法已被用于子信道分配、用戶聚類及功率分配等資源分配方法上[6-8]。

深度強化學習(DRL:Deep reinforcement learning)作為深度學習和強化學習的結合，可以直接從高維原始數據學習控制策略提供更快的收斂速度，對于具有多狀態和動作空間的系統更加有效。而深度Q網絡(DQN:Deep q-network)[9]是DRL的典型算法之一，它將神經網絡和Q學習結合起來，通過經驗回放和目標網絡來解決收斂和穩定問題。深度Q學習已經在許多研究中得到應用，例如多用戶蜂窩網絡中的功率控制[10]，多小區的功率分配[11]，以及物聯網系統[12-13]。

本文針對NOMA系統下資源配置問題，以優化系統最大和速率為目標展開研究。本文將該問題分解為2個子問題分步求解。首先根據信道條件將用戶分配至不同的子信道，然后再采用DQN算法，根據用戶信道狀態信息進行功率分配。通過仿真分析，基于DQN的功率分配方案可以得到較高的系統和速率。

2 系統模型

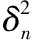
圖1 系統模型

系統總帶寬為B，將其均分為N個子信道，每個子信道的帶寬為Bs=B/N。用Sm，n表示子信道的分配索引。當用戶m分配在子信道n上時，Sm，n=1；否則，Sm，n=0。用pm，n表示第n個子信道上用戶m的分配功率。由于NOMA系統中多用戶可復用同一資源塊，設每個子信道上的最大用戶數為M。則第n個子信道上的傳輸信號為：

(1)

用gm，n表示子信道n上用戶m的信道增益。則基站接收端，接收信號的表達式為：

(2)

根據NOMA原理，在接收端采用串行干擾刪除技術(SIC)，基站接收多個不同用戶的疊加信號，將其按照一定的順序解調出來。在上行鏈路中，最優的SIC解碼順序應該是信道增益的降序[14]。因為具有較弱信道增益的設備不會對具有較強信道增益的設備造成干擾。對于子信道n中的用戶m，信干噪比可表示為：

(3)

根據香農定理，對應速率為：

Rm，n=Bslog (1+SINR)

(4)

子信道n的和速率為：

(5)

系統的和速率為：

(6)

由上述公式可以看出，系統的和速率和子信道分配、用戶的功率分配相關。因此，本文研究的是在上述場景下使系統的和速率最大化的問題，該優化問題可建模為：

(7)

其中，Pmax是用戶的最大發射功率，Rmin是用戶的最小數據速率。約束條件C1確保每個用戶的發射功率不超過Pmax。約束條件C2保證每個用戶的速率不低于最小信號速率。

由于在上述優化問題中，直接找出全局最優解的難度較高。本文將其分成2個子問題：子信道分配和功率分配，逐步去求解該優化問題。

3 子信道分配

在上行鏈路NOMA系統中，為了在基站接收端進行SIC，需要保持接收信號的差異性。而在同一子信道內，用戶的信道增益區別對于最小化簇內干擾也至關重要。用戶間信道增益差異越大，對系統性能的提升也越大。為減少接收端SIC解調的復雜度，在本文的分配方法中，每個子信道內將分配2個用戶。具體步驟如下。

子信道分配算法偽代碼

步驟1：輸入總用戶數K，組A={}，組B={}。

步驟2：將K個用按信道增益大小排序。

G=sort(K)={g1，g2……gK}

步驟3：如果用戶數K為偶數。

A={g1，g2……gK/2}

子信道數為K/2，具體分配為：

……

民間還成立有毛主席像章收藏研究會，總部設在上海。李建明感慨，當時那些收藏家們大都五六十歲了，自己還年輕。如今自己60多歲了，他們已經步入暮年。去年李建明去北京參加一個紅色收藏會議，見到幾位以前未曾謀面的老朋友，其中有位叫黃淼鑫，送他一本《追夢——毛主席像章收藏31年》。

SK/2={gK/2，gK}

步驟4：如果用戶數為奇數。

G=G-g(K+1)/2

步驟5：重復上述步驟3。

4 基于深度強化學習的功率分配

對于上行鏈路的NOMA系統資源分配，首先基于上述的子信道分配確定分配決策，再通過深度強化學習去確定用戶的功率分配。在明確具體的步驟之前，先簡要闡述強化學習的理論。

S(狀態空間)：在功率分配問題中，將用戶信號的信噪比看做狀態空間，信噪比r同用戶發射功率p、信道增益g等相關，因此，狀態空間S可表示為：

S={r1，r2……rK}

(8)

A(動作空間)：在NOMA功率分配中，將對用戶發射功率的調整看做是動作空間，可表示為：

A={-1，0，+1}

(9)

-1代表減少用戶的發射功率，+1代表增加用戶的發射功率，0表示維持不變。

Re(獎勵)：Re表示在狀態s下采取動作a得到獎勵，在本文中，將Re設為系統的優化目標和速率：

(10)

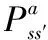
(11)

4.1 Q學習算法

Q學習(Q-learning)算法是一種時間差分算法。狀態-行為值函數(Q函數)表明智能體遵循策略π在某一狀態所執行的特定行為的最佳程度。Q函數定義為：

Qπ(s，a)=Eπ[Rt|st=s，at=a]

(12)

表示從狀態s開始采取動作a所獲得的期望回報。其中Rt表示所獲得的回報獎勵總和：

(13)

γ為折扣因子，表示對于未來獎勵和即時獎勵的重要性。γ取值位于0～1。

在本文的Q學習算法中，首先由系統環境獲得狀態s，并初始化Q函數；再根據ε貪婪策略在狀態s下采取動作a，轉移到新的狀態s′，獲取獎勵r。根據下列方程更新Q值，將其存入Q值表中。其中α為學習速率：

Q(s，a)=Q(s，a)+α(r+γmaxQ(s′，a′)-Q(s，a))

(14)

重復上述步驟若干次，直到迭代完成。

4.2 DQN算法

在具有多維狀態時，要遍歷每個狀態下的行為會花費大量時間，因此采用一個權重為θ的神經網絡來近似每個狀態下所有可能的Q值，即將該網絡作為函數逼近器來逼近Q函數，并通過梯度下降來最小化損失函數：

Loss(θ)=((r+γmaxQ(s′，a′，θ′)-Q(s，a，θ))2

(15)

在本課題中，對用戶進行子信道分配后，將其狀態空間輸入到DQN，采用ε貪婪策略來選擇動作：以概率ε在動作空間內選擇一個隨機動作，以概率1-ε選擇具有最大Q值的動作a：

a=argmax(Q(s，a，θ))

(16)

在選擇完動作后，在狀態s下執行該行為，然后轉移到新的狀態s′，并獲得獎勵r。上述信息〈s，a，r，s′〉將被保存至經驗回放池中。這些存儲信息可被用來訓練DQN。接下來，從經驗回放池中隨機采樣一批轉移信息，并計算損失函數Loss(θ)。由于連續的〈s，a，r，s′〉信息間是相關聯的，這些隨機采樣的訓練樣本將會減少信息之間的關聯性，并有助于降低神經網絡過擬合。

通過隨機選擇的訓練樣本，可以得到由目標網絡生成的Q值：

Qt=((r+γmaxQ(s′，a′，θ′))2

(17)

其中，目標網絡的權重為θ′。用于預測Q值的實際Q網絡可通過梯度下降來學習正確的權重。滯后若干時間步后，從實際Q網絡中復制權重θ來更新目標Q網絡的權重θ′，這樣可使訓練過程進一步穩定。如圖2所示。

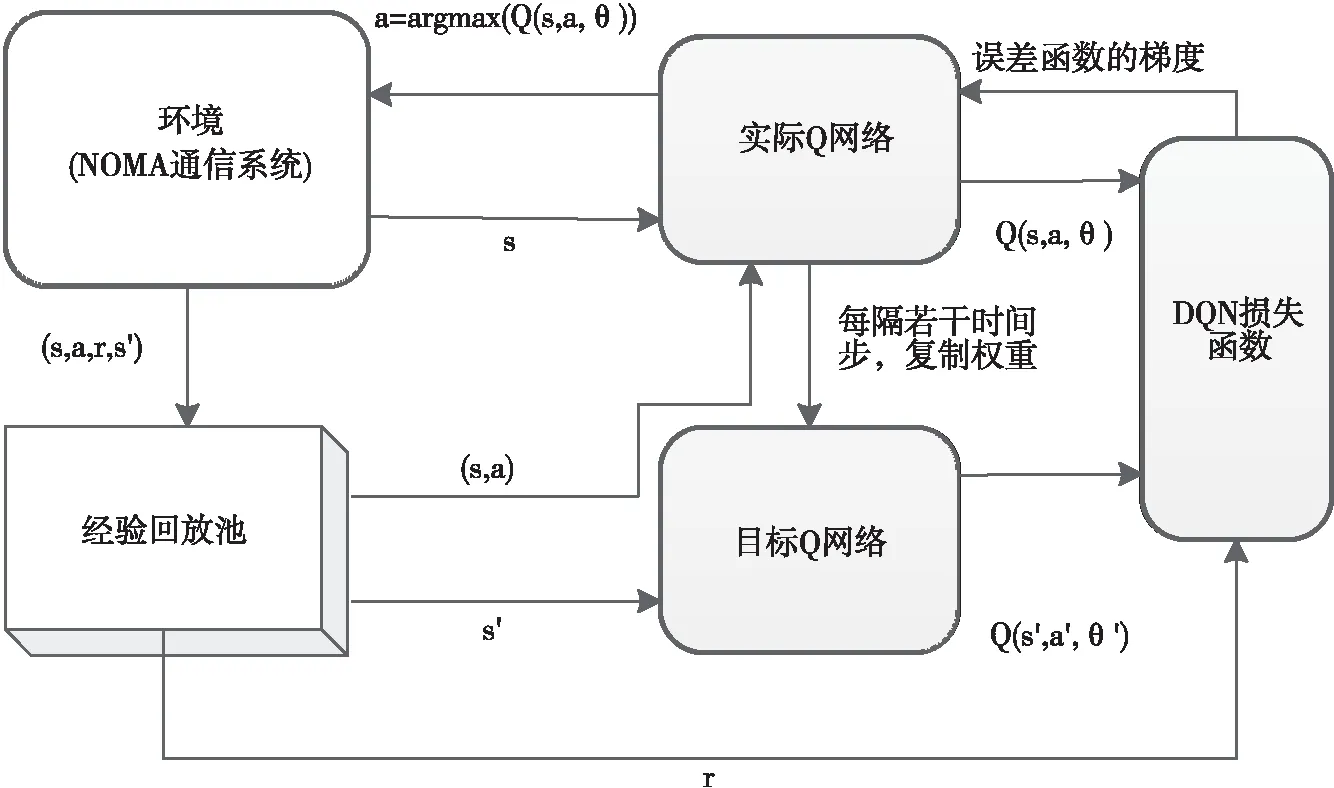
圖2 DQN主要流程圖

5 結果及分析

在本節中，通過仿真結果來評估上行鏈路NOMA系統中深度強化學習算法的有效性。基站位于小區中心，用戶隨機分布在小區內。具體參數設置如表1所示。此次仿真在Python3.6上用Tensorflow1.5完成。

表1 仿真參數設置

圖3對比了DQN和Q-learning算法的收斂速度和平均和速率。可以看出DQN相較于Q-learning算法更加穩定，相同迭代條件內且所能達到的平均和速率更大，收斂速度更快。這是因為基于神經網絡的DQN算法搜索更快，且在狀態數過多時，不容易陷入局部最優。

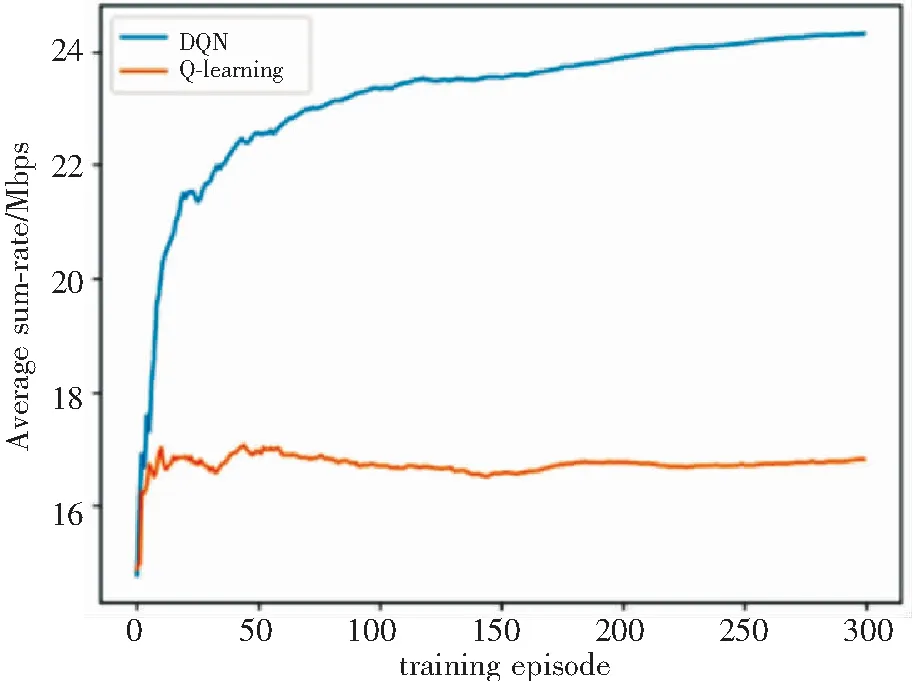
圖3 算法的平均和速率比較

圖4對比了不同發射功率下DQN，Q-learning以及固定功率分配算法(FPA :Fixed power allocation)的平均和速率。當用戶設備采用FPA算法進行功率分配時，可獲得略優于Q-learning算法的平均和速率；但FPA始終采用最大發射功率，會導致較高的能量損耗；而DQN由于收斂較快，始終能達到較高的和速率，并且使功率動態分配。

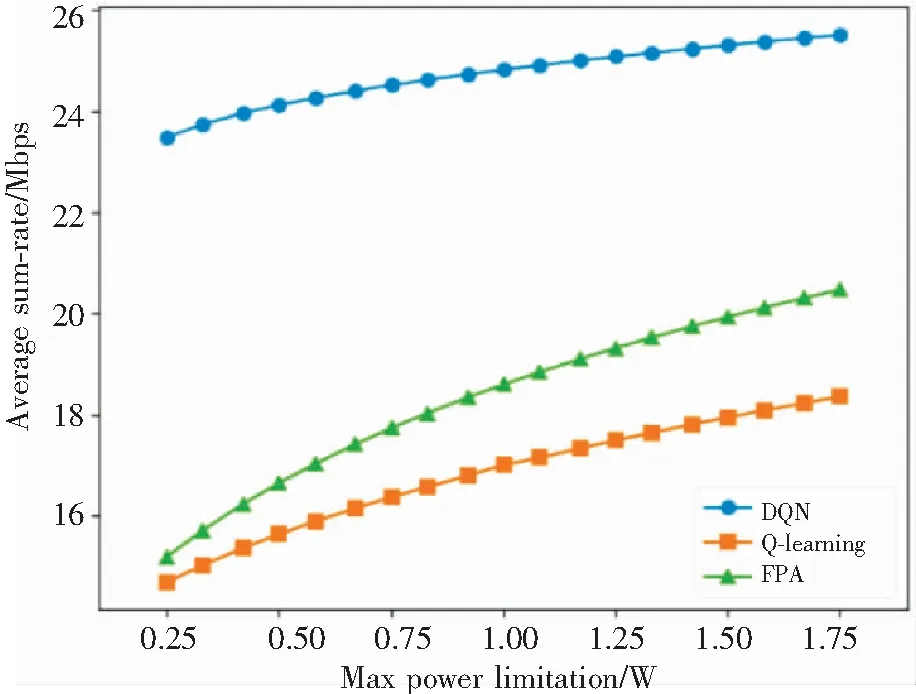
圖4 不同功率限制下和速率比較

圖5對比了在不同學習速率下的DQN損失函數的收斂情況。學習速率過大會導致函數震蕩，迭代過快；學習速率過小則會使函數收斂過慢。從圖5中可以看出，當學習速率(learning rate)設置為0.01時，DQN的收斂更加穩定。

圖5 不同學習速率下的DQN損失函數

6 結語

本文主要研究了上行鏈路NOMA系統資源分配問題，通過子信道分配和基于信道條件的DQN功率分配算法，找到較優的功率分配方案，實現了最大化系統和速率的目標。仿真結果顯示:本文提出的Q-learning算法和DQN具備較快的收斂特性。與其他方法相比，DQN算法可以實現更高的和速率，表現出了更好的性能。