采用核極限學(xué)習(xí)機(jī)的短期需水量預(yù)測(cè)模型

韓宏泉，吳 珊，侯本偉

(北京工業(yè)大學(xué) 城市建設(shè)學(xué)部，北京 100124)

短期需水量預(yù)測(cè)模型在有限的預(yù)測(cè)區(qū)間(從1個(gè)月到1天不等)內(nèi)進(jìn)行需水量預(yù)測(cè)，預(yù)測(cè)時(shí)間步長(zhǎng)通常控制在每天到每小時(shí)，其在給水系統(tǒng)的優(yōu)化調(diào)度與日常管理中發(fā)揮著重要作用[1-2]。以往的短期需水量預(yù)測(cè)模型一般面向整個(gè)城市[3-6]，預(yù)測(cè)步長(zhǎng)多以小時(shí)和天為時(shí)間步長(zhǎng)，主要應(yīng)用于城市水量的供需平衡分析。近年來(lái)，隨著硬件采集技術(shù)的發(fā)展，收集步長(zhǎng)為1～15 min的觀測(cè)數(shù)據(jù)成為可能，物聯(lián)網(wǎng)、云計(jì)算等新技術(shù)也不斷融入水務(wù)行業(yè)，期望從供水系統(tǒng)大數(shù)據(jù)的研究中挖掘出更多工程應(yīng)用價(jià)值。在此背景下，在線調(diào)度、壓力分區(qū)調(diào)控、漏損控制、爆管監(jiān)測(cè)等供水系統(tǒng)工程對(duì)短期需水量預(yù)測(cè)提出了新的速度和時(shí)間尺度需求。

很多學(xué)者對(duì)需水量預(yù)測(cè)方法進(jìn)行了研究，早期傳統(tǒng)的統(tǒng)計(jì)學(xué)方法因易于理解和實(shí)施得到了大量的應(yīng)用，然而，由于自身的局限性很多時(shí)候并不能達(dá)到良好的預(yù)測(cè)效果[2]，例如，多元線性回歸算法預(yù)設(shè)了特征與需水量之間的關(guān)系；指數(shù)平滑算法對(duì)其加權(quán)系數(shù)缺乏客觀的識(shí)別方法；自回歸移動(dòng)平均算法要求時(shí)序數(shù)列是平穩(wěn)的或者經(jīng)差分處理后是平穩(wěn)的，且本質(zhì)上只能捕捉線性關(guān)系，而真實(shí)需水量的變化是非線性的，且具有隨機(jī)性。近年來(lái)，機(jī)器學(xué)習(xí)方法被更多地應(yīng)用于短期需水量預(yù)測(cè)中，機(jī)器學(xué)習(xí)方法是典型的數(shù)據(jù)驅(qū)動(dòng)算法，通過(guò)歷史數(shù)據(jù)來(lái)深入挖掘需水量與相關(guān)變量之間的關(guān)系，從而提高預(yù)測(cè)模型的穩(wěn)定性和可靠性。其中，人工神經(jīng)網(wǎng)絡(luò)算法(artificial neural network，ANN)和支持向量回歸算法(support vector regression，SVR)以及它們的擴(kuò)展方法在文獻(xiàn)中介紹最多[3-5]，研究中也多使用二者與新提出的機(jī)器學(xué)習(xí)模型進(jìn)行性能比較，從而對(duì)新模型進(jìn)行評(píng)估。

除ANN與SVR外，極限學(xué)習(xí)機(jī)算法(extreme learning machine，ELM)由于比傳統(tǒng)機(jī)器學(xué)習(xí)方法擁有更快的訓(xùn)練速度，近來(lái)也被應(yīng)用于預(yù)測(cè)模型中，但其實(shí)際應(yīng)用效果表現(xiàn)出一定的差異性[6-8]。Huang等[9]在ELM的基礎(chǔ)上提出了核極限學(xué)習(xí)機(jī)(kernel-based extreme learning machine，KELM)算法，該算法繼承了ELM較高的訓(xùn)練速度的優(yōu)點(diǎn)的同時(shí)，被證明相比ELM具有更加穩(wěn)定的性能并且有著與SVR相似的泛化能力[10]，但該方法目前尚未在短期需水量預(yù)測(cè)領(lǐng)域得到更多嘗試。

研究人員除了不斷追求單獨(dú)預(yù)測(cè)模型效率的提高外，近來(lái)更多地傾向于組合模型的研究[11-12]，通過(guò)對(duì)兩種或多種預(yù)測(cè)模型進(jìn)行組合以形成優(yōu)勢(shì)互補(bǔ)，來(lái)提高整體預(yù)測(cè)效果。其中，傅里葉級(jí)數(shù)模型(Fourier series，F(xiàn)S)因?qū)崿F(xiàn)簡(jiǎn)單且需要較少的訓(xùn)練數(shù)據(jù)而常用于與機(jī)器學(xué)習(xí)模型進(jìn)行組合[13-14]。本研究充分利用數(shù)據(jù)信息，將短期需水量的預(yù)測(cè)步長(zhǎng)控制在15 min，引入了KELM模型以提高短期需水量預(yù)測(cè)的速度，同時(shí)，提出了以KELM模型為初始預(yù)測(cè)模塊疊加使用FS模塊進(jìn)行殘差修正的組合模型(KELM+FS)，以進(jìn)一步提升預(yù)測(cè)精度。

1 方法原理

本研究提出的基于核極限學(xué)習(xí)機(jī)的短期需水量預(yù)測(cè)模型KELM通過(guò)對(duì)樣本數(shù)據(jù)進(jìn)行訓(xùn)練，建立起歷史時(shí)刻需水量與目標(biāo)時(shí)刻需水量之間的非線性關(guān)系，進(jìn)而根據(jù)歷史數(shù)據(jù)實(shí)現(xiàn)對(duì)目標(biāo)時(shí)刻需水量的預(yù)測(cè)。模型為多維輸入單維輸出，輸入特征為與目標(biāo)時(shí)刻需水量數(shù)據(jù)高度相關(guān)的歷史需水量數(shù)據(jù)，輸出為目標(biāo)時(shí)刻的需水量預(yù)測(cè)值。KELM+FS模型中的殘差修正模塊FS則利用傅里葉級(jí)數(shù)對(duì)KELM的預(yù)測(cè)值與觀測(cè)值之間的差值進(jìn)行建模，識(shí)別出殘差序列中隱含的周期性規(guī)律，從而完成對(duì)未來(lái)時(shí)刻殘差的推測(cè)，其輸入為T個(gè)歷史殘差數(shù)據(jù)，輸出為整個(gè)預(yù)測(cè)區(qū)間的殘差序列。

1.1 極限學(xué)習(xí)機(jī)原理

ELM是在單隱含層前饋神經(jīng)網(wǎng)絡(luò)的基礎(chǔ)上提出的。與傳統(tǒng)單隱含層前饋神經(jīng)網(wǎng)絡(luò)使用梯度下降法迭代求解網(wǎng)絡(luò)參數(shù)不同，ELM在訓(xùn)練過(guò)程中隨機(jī)生成輸入權(quán)值ω和偏置b且不再調(diào)整，將最優(yōu)求解問(wèn)題轉(zhuǎn)化為簡(jiǎn)單的最小二乘求解問(wèn)題，這使得ELM具有了更快的學(xué)習(xí)和運(yùn)行速度[15]。應(yīng)用中ELM的訓(xùn)練機(jī)理可以簡(jiǎn)單描述如下[6,15-16]：

假設(shè)給定訓(xùn)練樣本{xi,yi|xi∈RD,i=1,…,n}(其中xi表示第i個(gè)樣本的D維輸入向量xi=[xi1,…,xiD]，yi對(duì)應(yīng)著第i個(gè)樣本的觀測(cè)數(shù)據(jù))，隱含層神經(jīng)元數(shù)為k，根據(jù)ELM網(wǎng)絡(luò)定義可以寫出如下表達(dá)式：

(1)

當(dāng)ELM的輸出結(jié)果能夠以零誤差逼近觀測(cè)數(shù)據(jù)時(shí)，利用矩陣表達(dá)可以寫為如下形式：

Hβ=Y

(2)

式中：H為隱含層輸出矩陣，Y=[y1,…,yn]T為觀測(cè)向量。

在ELM訓(xùn)練過(guò)程中，ω和b采取隨機(jī)生成的方法確定，為計(jì)算網(wǎng)絡(luò)的輸出結(jié)果，β是唯一需要求解的參數(shù)[17]。

以最小訓(xùn)練誤差和最小輸出權(quán)的范數(shù)為求解目標(biāo)，根據(jù)線性代數(shù)知識(shí)，方程(2)的最小范數(shù)最小二乘解為[18]

β=H+Y=(HTH)-1HTY

(3)

其中H+為隱含層輸出矩陣H的Moore-Penrose廣義逆矩陣。

1.2 核極限學(xué)習(xí)機(jī)原理

為了進(jìn)一步簡(jiǎn)化ELM的應(yīng)用，避免在確定隱含層神經(jīng)元數(shù)時(shí)應(yīng)用耗時(shí)的算法和隨機(jī)分配權(quán)重的潛在缺點(diǎn)，Huang等[18]在ELM的基礎(chǔ)上提出了KELM，KELM隱含層的映射不再采用g(*)這種簡(jiǎn)單的顯式形式而是采用核矩陣確定，而且隱含層神經(jīng)元數(shù)不再需要指定，在這種情況下KELM比ELM具有更穩(wěn)定的性能，并且KELM與SVR具有相似的泛化能力[10]。KELM的機(jī)制在ELM的基礎(chǔ)上可以描述如下[9,18-19]。

為增加模型的穩(wěn)定性和泛化能力，在對(duì)β的求解中將引入一個(gè)正數(shù)C，并以最小訓(xùn)練誤差和最小輸出權(quán)的范數(shù)為求解目標(biāo)[20]，則有

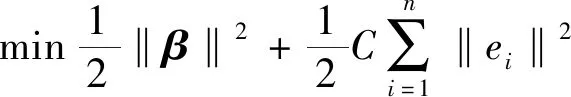
(4)

式中：ei為訓(xùn)練誤差，h(x)為隱含層特征映射函數(shù)。

(5)

此時(shí)β被計(jì)算為

β=HT(I/C+HHT)-1Y

(6)

對(duì)于KELM來(lái)說(shuō)不必知道其映射函數(shù)的具體形式，而是構(gòu)造隱式映射來(lái)代替，即構(gòu)造核矩陣來(lái)代替HTH，則有

ΩELM=HHT
ΩELMi,j=h(xi)h(xj)=K(xi,xj)

(7)

最終網(wǎng)絡(luò)輸出結(jié)果可寫為

(8)

式中：ΩELM為核矩陣，K(xi,xj)為核函數(shù)。在KELM中有多種核函數(shù)可供選擇，比如線性核函數(shù)(linear)、多項(xiàng)式核函數(shù)(polynomial)、高斯徑向基核函數(shù)(rbf)等[19]。圖1中給出了ELM與KELM多維輸入單維輸出的經(jīng)典結(jié)構(gòu)，其中a為ELM的映射函數(shù)，b為KELM的映射函數(shù)。

圖1 多維輸入單維輸出的ELM和KELM經(jīng)典結(jié)構(gòu)Fig.1 Typical structures of ELM and KELM with multidimensional input and one-dimensional output

1.3 傅里葉級(jí)數(shù)原理

傅里葉級(jí)數(shù)能夠?qū)⒅芷谛盘?hào)或函數(shù)展開為一組不同頻率三角函數(shù)的和，通過(guò)將周期內(nèi)的歷史時(shí)間序列數(shù)據(jù)擬合為傅里葉級(jí)數(shù)方程來(lái)實(shí)現(xiàn)對(duì)未來(lái)時(shí)刻數(shù)據(jù)的推斷。假設(shè)一個(gè)周期由T個(gè)時(shí)刻組成，將此周期在[0,2π]區(qū)間內(nèi)進(jìn)行標(biāo)準(zhǔn)化，則有

(9)

此時(shí)傅里葉級(jí)數(shù)方程可以定義為

(10)

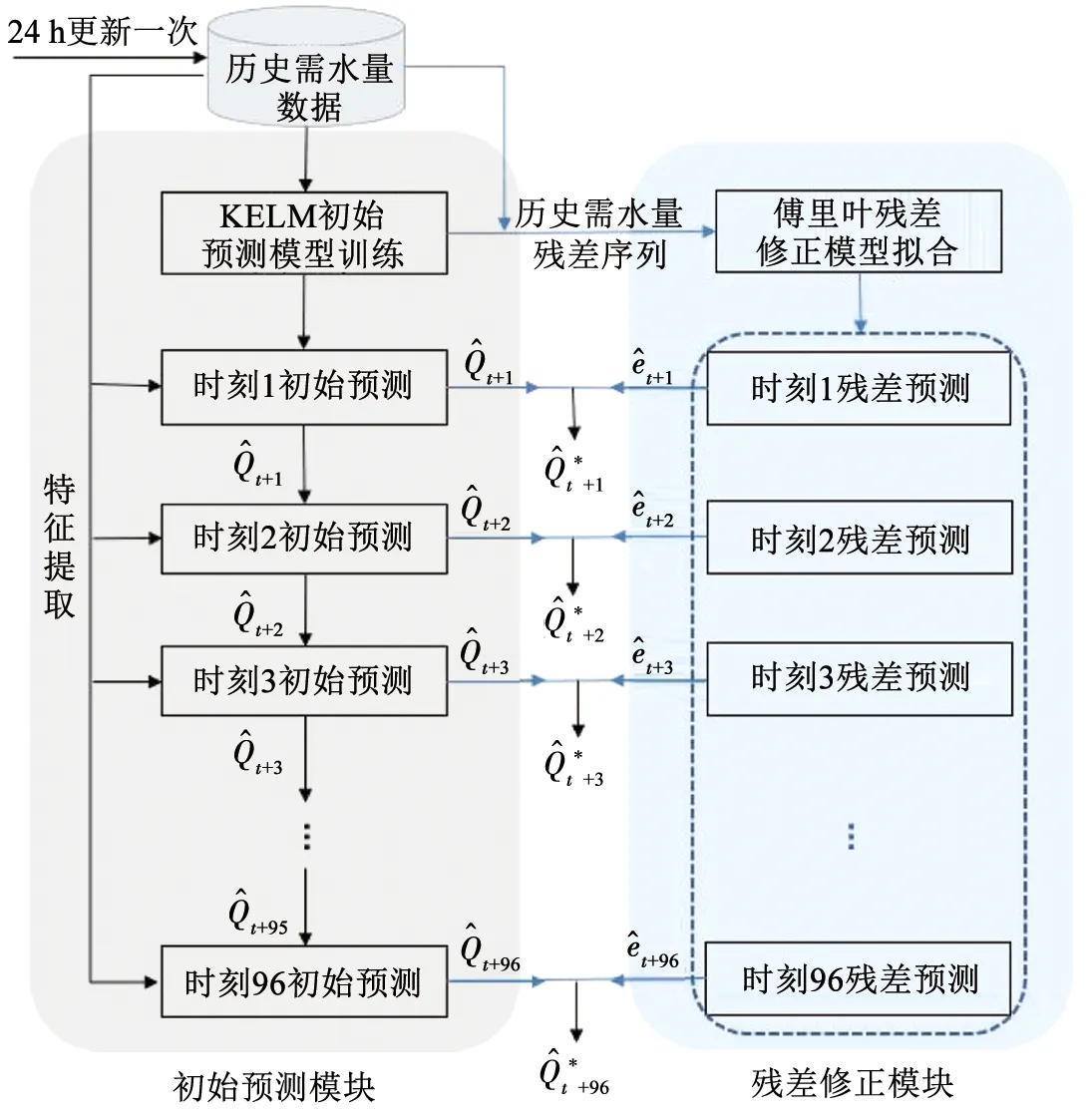
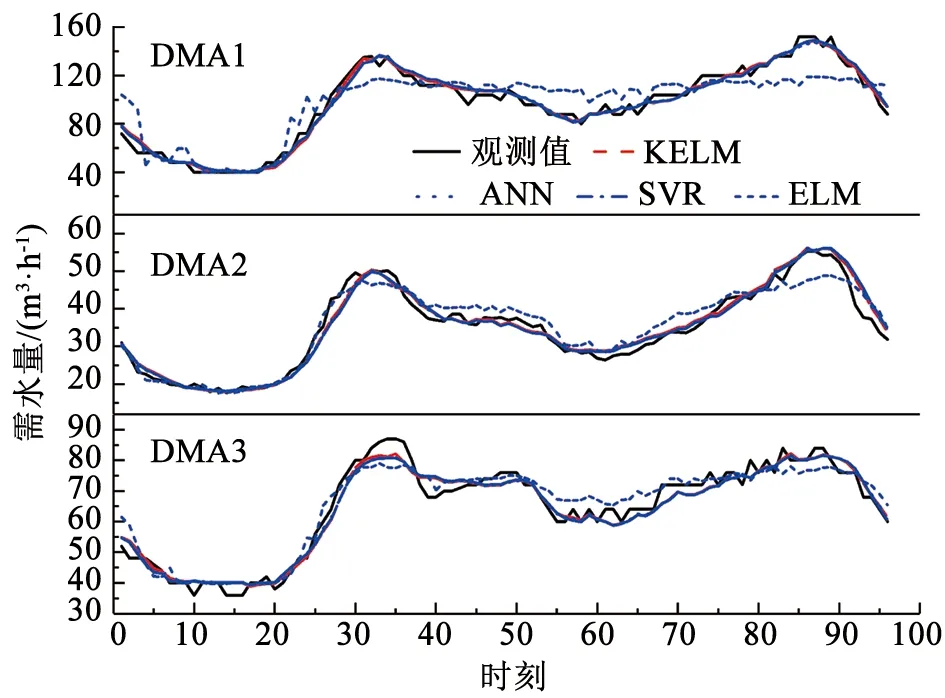
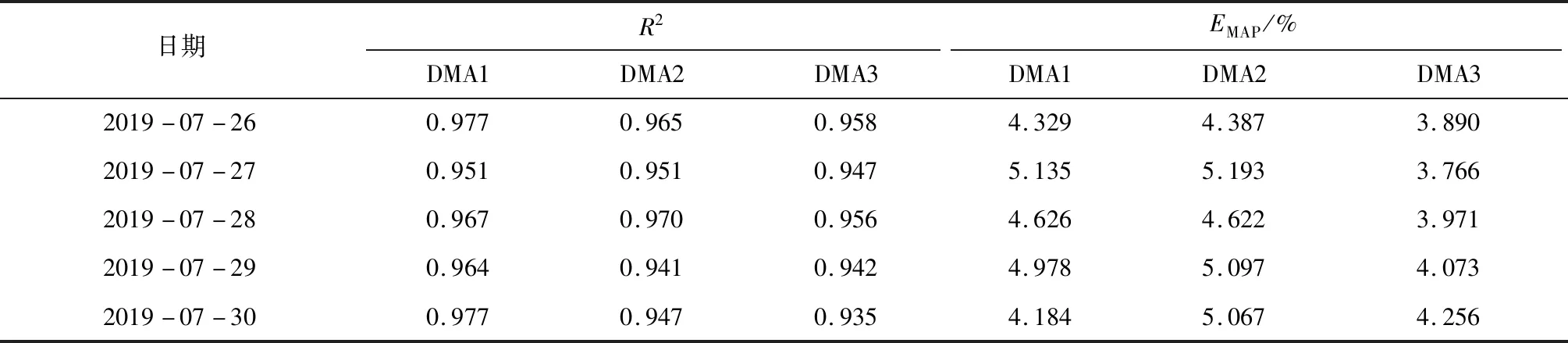
式中：tq為經(jīng)過(guò)標(biāo)準(zhǔn)化的時(shí)刻；M為傅里葉多項(xiàng)式的級(jí)數(shù)，M

以觀測(cè)值f(tq)與傅里葉級(jí)數(shù)方程估計(jì)值f*(tq)之間差值的二范數(shù)作為目標(biāo)函數(shù)，傅里葉級(jí)數(shù)方程的系數(shù)可以通過(guò)最小二乘法確定[13]：

(11)

本研究中，首先選定殘差周期，將一個(gè)殘差周期內(nèi)的歷史時(shí)刻進(jìn)行標(biāo)準(zhǔn)化處理，然后根據(jù)式(11)的系數(shù)表達(dá)式，將周期內(nèi)的殘差序列值f(tq)以及標(biāo)準(zhǔn)化時(shí)刻tq依次代入式中，便可計(jì)算出相應(yīng)的系數(shù)a0、ap和bp，從而實(shí)現(xiàn)傅里葉級(jí)數(shù)方程的擬合，繼而根據(jù)殘差序列所蘊(yùn)含的周期性特征，可使用擬合好的傅里葉級(jí)數(shù)方程推測(cè)未來(lái)時(shí)刻的殘差值。

2 建模流程

本研究所提出的短期需水量預(yù)測(cè)模型是在預(yù)測(cè)區(qū)間為24 h，預(yù)測(cè)步長(zhǎng)為15 min的條件下建立的。根據(jù)監(jiān)測(cè)條件，觀測(cè)數(shù)據(jù)每15 min進(jìn)行一次采樣，每24 h進(jìn)行一次傳輸，即歷史數(shù)據(jù)集每24 h進(jìn)行一次更新。歷史數(shù)據(jù)集的大小始終保持不變，采用移動(dòng)窗口更新，即當(dāng)增添最近96個(gè)時(shí)刻的觀測(cè)數(shù)據(jù)的同時(shí)會(huì)刪除最早的96個(gè)時(shí)刻的數(shù)據(jù)。

2.1 輸入特征選擇

選擇合適的輸入特征對(duì)模型的建立十分重要。Guo[2]、Bakker[21]、Cutore等[22]在建立短期需水量預(yù)測(cè)模型時(shí)都僅選擇歷史需水量作為唯一輸入特征，并且證明了在這一條件下可以實(shí)現(xiàn)可靠的預(yù)測(cè)。本研究同樣使用歷史需水量數(shù)據(jù)作為模型的唯一輸入特征。

綜合參考Guo[2]、Herrera[3]以及Odan等[13]的輸入特征選擇方案，并通過(guò)相關(guān)性分析和模型預(yù)測(cè)實(shí)驗(yàn)，最終選擇{當(dāng)前時(shí)刻，前1 d的目標(biāo)時(shí)刻，前2 d的目標(biāo)時(shí)刻，前1周的目標(biāo)時(shí)刻}的用水需求數(shù)據(jù)作為模型的輸入特征，即{Qt,Qt-95,Qt-191,Qt-671}。預(yù)測(cè)期間Qt-95，Qt-191和Qt-671使用對(duì)應(yīng)的歷史觀測(cè)數(shù)據(jù)作為輸入；在第1個(gè)目標(biāo)時(shí)刻時(shí)，Qt使用對(duì)應(yīng)的歷史觀測(cè)數(shù)據(jù)，從第2個(gè)目標(biāo)時(shí)刻開始，Qt使用上一時(shí)刻的初始預(yù)測(cè)值作為下一時(shí)刻的特征輸入。

2.2 KELM模型建立步驟

1)收集并通過(guò)數(shù)據(jù)清洗對(duì)歷史需水量數(shù)據(jù)進(jìn)行預(yù)處理。

2)提取歷史需水量數(shù)據(jù)的輸入特征輸入到預(yù)測(cè)模型中，通過(guò)KELM訓(xùn)練，建立歷史需水量數(shù)據(jù)與下一時(shí)刻需水量數(shù)據(jù)之間的聯(lián)系，從而實(shí)現(xiàn)KELM模型的建立。

2.3 KELM+FS模型建立步驟

KELM+FS的建立主要包括建立需水量初始預(yù)測(cè)模塊和建立殘差修正模塊兩部分。圖2展示了模型建立的流程。其中需水量初始預(yù)測(cè)模塊的構(gòu)建步驟與KELM模型相同，不再贅述。主要建模步驟如下：

圖2 KELM+FS模型建立流程Fig.2 Flow chart of KELM+FS model building

1)建立需水量初始預(yù)測(cè)模塊。

2)通過(guò)建模訓(xùn)練的歷史需水量數(shù)據(jù)、初始預(yù)測(cè)模塊對(duì)訓(xùn)練數(shù)據(jù)擬合(預(yù)測(cè))結(jié)果，獲得初始預(yù)測(cè)模型對(duì)建模數(shù)據(jù)的的殘差序列e=[e1,e2,…,eT]T。

(12)

4)計(jì)算目標(biāo)時(shí)刻的最終需水量預(yù)測(cè)值：

(13)

2.4 評(píng)價(jià)指標(biāo)

目前已有很多方法應(yīng)用于需水量預(yù)測(cè)模型的性能評(píng)價(jià)，本研究采用已廣為接受的指標(biāo)作為模型的評(píng)價(jià)指標(biāo)，其中包括用于評(píng)估預(yù)測(cè)精度的擬合優(yōu)度(R2)[2,8,14]、平均絕對(duì)百分比誤差(MAPE,EMAP)[2,14,23]以及用于評(píng)價(jià)計(jì)算速度的模型計(jì)算時(shí)間。具體計(jì)算公式如下：

(14)

(15)

3 實(shí)例分析

3.1 數(shù)據(jù)描述

采用某城市3個(gè)真實(shí)的獨(dú)立計(jì)量區(qū)(DMA)歷史需水量數(shù)據(jù)進(jìn)行預(yù)測(cè)實(shí)驗(yàn)對(duì)提出的模型進(jìn)行驗(yàn)證。這3個(gè)DMA的組成結(jié)構(gòu)相似，大部分用戶為居民用戶，包含少量商業(yè)用戶，屬于典型的城市住宅區(qū)DMA。獲取數(shù)據(jù)的時(shí)間范圍為2019年6月1日—2019年7月30日，采樣間隔為15 min。表1給出收集數(shù)據(jù)時(shí)間范圍內(nèi)這3個(gè)DMA的基本數(shù)據(jù)特征，其中DMA1的平均需水量最高，且相比具有更高的隨機(jī)波動(dòng)性；DMA2平均需水量最低；DMA3需水量數(shù)據(jù)變異系數(shù)最低。研究以2019年7月26日96個(gè)時(shí)刻的需水量數(shù)據(jù)作為測(cè)試數(shù)據(jù)，將其前55 d的數(shù)據(jù)通過(guò)特征提取后作為模型的建立數(shù)據(jù)，其中90%作為訓(xùn)練集，10%作為驗(yàn)證集。訓(xùn)練集與驗(yàn)證集用于尋找模型參數(shù)并建立模型，測(cè)試集則用于測(cè)試所建立模型的性能。

表1 3個(gè)DMA的基本需水量數(shù)據(jù)信息Tab.1 Basic water demand data for three DMAs

3.2 模型參數(shù)

為了對(duì)所提出的模型進(jìn)行客觀評(píng)估，引入了已被廣泛使用的ANN模型、SVR模型，以及KELM的同源模型——ELM模型和添加了殘差修正模塊的組合模型一起參與性能測(cè)試。所有模型的建立均以MATLAB 2016b為平臺(tái)，所用計(jì)算機(jī)CPU型號(hào)為 Inter Core i7-10510U，內(nèi)存為16.0 GB。

其中ANN模型采用單層前饋架構(gòu)構(gòu)建，并使用廣為接受的反向傳播算法進(jìn)行訓(xùn)練，其隱含層神經(jīng)元數(shù)k為該模型主要待定參數(shù)，采用logn[24](n為訓(xùn)練樣本數(shù))和2D+1[25](D為輸入特征維數(shù))確定隱含層神經(jīng)元的上下限，并通過(guò)試錯(cuò)法將產(chǎn)生最小泛化誤差的神經(jīng)元數(shù)確定為最優(yōu)隱含層神經(jīng)元數(shù)[26]。

有關(guān)SVR的理論已有很多研究人員進(jìn)行過(guò)詳細(xì)敘述，具體見(jiàn)文獻(xiàn)[4,27-28]。建立該模型需要確定的主要參數(shù)有核函數(shù)、不敏感系數(shù)ε、懲罰因子C、核函數(shù)寬度系數(shù)γ。研究中選擇徑向基函數(shù)(RBF)作為核函數(shù)。不敏感系數(shù)ε選取平臺(tái)默認(rèn)值0.1，C和γ的取值分別設(shè)為{21,22,…，25}和{2-5,2-4,…,2-1}[19]，于建模數(shù)據(jù)中使用網(wǎng)格搜索和5折交叉驗(yàn)證在取值范圍內(nèi)進(jìn)行二者的組合尋優(yōu)。

根據(jù)1.1節(jié)ELM基礎(chǔ)原理，ELM模型待定參數(shù)為隱含層神經(jīng)元數(shù)k和激活函數(shù)類型。參考Mouatadid等[6]對(duì)于ELM模型的訓(xùn)練方案，選取Sig作為激活函數(shù)，將k的取值設(shè)定為{10,20,…,200}，使用試錯(cuò)法在泛化誤差最小時(shí)獲取k的最佳取值。

根據(jù)1.2節(jié)KELM基礎(chǔ)原理可知，建立該模型需要確定的參數(shù)包括核函數(shù)、懲罰因子C。經(jīng)過(guò)試驗(yàn)選定linear作為核函數(shù)，將懲罰因子C的取值設(shè)為{2-20,2-19,…,2-10}[9]，使用試錯(cuò)法在泛化誤差最小時(shí)獲取最佳參數(shù)取值。

組合模型*+FS由初始預(yù)測(cè)模塊和FS殘差修正模塊耦合而成，初始預(yù)測(cè)模塊的參數(shù)確定方法與前述單獨(dú)模型的方法一致。對(duì)于FS模塊，Odan和Reis[13]在建立FS模型時(shí)指出按照每7 d為一個(gè)周期對(duì)傅里葉系數(shù)進(jìn)行計(jì)算且每24 h進(jìn)行一次更新是足夠的，本研究采用與之相同的計(jì)算和更新策略，將FS模塊一周期所包含的時(shí)刻數(shù)設(shè)為T=7×96=672，此時(shí)，傅里葉級(jí)數(shù)M應(yīng)該滿足M

表2給出了實(shí)驗(yàn)中各模型的主要參數(shù)取值。

表2 各單獨(dú)模型的主要參數(shù)取值Tab.2 Main parameter values of each single model

3.3 結(jié)果分析

表3給出不同模型對(duì)3個(gè)DMA進(jìn)行連續(xù)24 h且步長(zhǎng)為15 min的短期需水量預(yù)測(cè)評(píng)價(jià)結(jié)果。

3.3.1 KELM模型性能分析

對(duì)于預(yù)測(cè)日，步長(zhǎng)為15 min的觀測(cè)值曲線和各單獨(dú)模型預(yù)測(cè)值曲線見(jiàn)圖3。

KELM模型能夠產(chǎn)生與SVR、ANN模型相似的精度。根據(jù)表3統(tǒng)計(jì)數(shù)據(jù)可知，研究所引入的KELM模型在3個(gè)DMA的預(yù)測(cè)測(cè)試中都產(chǎn)生了與廣為應(yīng)用的ANN和SVR相近的較高精度。以指標(biāo)R2為例，ANN、SVR、KELM模型在3個(gè)DMA測(cè)試中評(píng)價(jià)結(jié)果的均值分別為0.96、0.96和0.97。觀察圖3也可以看出,KELM、ANN、SVR的預(yù)測(cè)曲線非常接近并且與觀測(cè)值曲線趨勢(shì)一致，同時(shí)較好地捕捉了曲線峰谷變化。

與ELM模型相比，KELM模型的表現(xiàn)更加穩(wěn)定。ELM模型在3個(gè)DMA短期需水量測(cè)試中表現(xiàn)出了較大差異，如對(duì)歷史需水量數(shù)據(jù)變異系數(shù)最高的DMA1進(jìn)行預(yù)測(cè)時(shí)，其評(píng)價(jià)指標(biāo)R2僅為0.76，EMAP也高達(dá)12%以上，而對(duì)其他兩個(gè)DMA的測(cè)試中R2均達(dá)到了0.9以上；KELM模型則始終發(fā)揮穩(wěn)定，R2保持在0.95以上。從圖3中還可觀察到相比其他單獨(dú)模型，ELM在對(duì)波峰波谷(時(shí)刻30～ 35，時(shí)刻85～ 90)的識(shí)別中也明顯不夠準(zhǔn)確。此外，從表3數(shù)據(jù)可以看出，增加修正模塊FS后，原本精度較低的ELM模型，得到的周期性殘差補(bǔ)償更為明顯，這也可從側(cè)面說(shuō)明，KELM模型相比ELM模型能夠更多地識(shí)別周期性現(xiàn)象并將其耦合到自身的預(yù)測(cè)過(guò)程中。

表3 各預(yù)測(cè)模型在測(cè)試集中的評(píng)價(jià)結(jié)果Tab.3 Performance indicators of prediction models ontest set

圖3 各單獨(dú)模型預(yù)測(cè)值與觀測(cè)值曲線Fig.3 Curves of predicted and observed values of each single model

除了在計(jì)算精度和穩(wěn)定性方面表現(xiàn)優(yōu)良外，KELM模型的更大優(yōu)勢(shì)體現(xiàn)在其計(jì)算速度上。KELM與ELM一樣，在訓(xùn)練過(guò)程中不再調(diào)整隱含層參數(shù)，使得模型訓(xùn)練所需時(shí)間明顯下降，其在3個(gè)DMA的預(yù)測(cè)實(shí)驗(yàn)中均未超過(guò)7 s，這也預(yù)示著其在產(chǎn)生與ANN、SVR相似的精度時(shí)只需花費(fèi)二者平均時(shí)間的5%左右。

為了測(cè)試KELM模型的泛化能力，使用KELM模型對(duì)3個(gè)DMA分別進(jìn)行了連續(xù)5 d(2019年7月26日—2019年7月30日)的需水量預(yù)測(cè)實(shí)驗(yàn)，其中2019年7月26日、29日和30日為工作日，2019年7月27日和28日為休息日，訓(xùn)練模型時(shí)使用每個(gè)預(yù)測(cè)日前55 d數(shù)據(jù)提取特征后的90%作為訓(xùn)練集，10%作為驗(yàn)證集。表4給出了對(duì)應(yīng)的評(píng)價(jià)結(jié)果，以R2為例，KELM模型在3個(gè)DMA中的平均精度為0.97、0.95和0.95，表現(xiàn)出良好的精度效果。圖4給出了連續(xù)預(yù)測(cè)中步長(zhǎng)為15 min的預(yù)測(cè)值與觀測(cè)值曲線，預(yù)測(cè)值始終表現(xiàn)出與觀測(cè)值非常一致的趨勢(shì)，也較為準(zhǔn)確地捕捉到了峰谷變化。此外，3個(gè)DMA工作日和休息日的EMAP平均值分別為4.47% 和4.55%，對(duì)于工作日與休息日的預(yù)測(cè)精度并無(wú)較大差別。可見(jiàn)，KELM模型在應(yīng)對(duì)連續(xù)預(yù)測(cè)休息日與工作日的不同時(shí)能夠表現(xiàn)出良好的泛化能力。

表4 KELM模型連續(xù)5 d預(yù)測(cè)的結(jié)果評(píng)價(jià)Tab.4 Performance indicators of KELM prediction model on five consecutive days

圖4 KELM模型連續(xù)5 d的預(yù)測(cè)值與觀測(cè)值曲線Fig.4 Curves of predicted and observed values of KELM model on five consecutive days

3.3.2 KELM+FS模型性能分析

測(cè)試結(jié)果表明，為KELM模型增加修正模塊FS后，其精度得到了一定程度的提升。表3的統(tǒng)計(jì)數(shù)據(jù)顯示，KELM+FS模型在對(duì)3個(gè)DMA的需水量預(yù)測(cè)實(shí)驗(yàn)中在所有模型中精度表現(xiàn)最佳，相比KELM模型，以EMAP指標(biāo)為例，KELM+FS模型在3個(gè)DMA上的相對(duì)降幅分別為12.0%、17.2%和8.4%。事實(shí)上，增加修正模塊后精度提高不僅限于KELM+FS模型，圖5展示了所有單獨(dú)模型及其組合模型的絕對(duì)百分比誤差(APE，EAP)箱線圖。可以看出，經(jīng)過(guò)殘差修正的模型相比對(duì)應(yīng)的單獨(dú)模型無(wú)論是在EAP的數(shù)值范圍、平均值，還是中位數(shù)方面都有所下降，這也在一定程度上驗(yàn)證了研究中所應(yīng)用的修正模塊的確可以捕捉殘差序列中蘊(yùn)含的周期性特征，并將其補(bǔ)償?shù)阶罱K預(yù)測(cè)結(jié)果中，發(fā)揮進(jìn)一步降低單獨(dú)模型誤差的作用。

圖5 各模型絕對(duì)百分比誤差箱線圖Fig.5 Boxplot of absolute percentage error of each model

綜合來(lái)看，所提出的KELM+FS組合模型除擁有較高的預(yù)測(cè)精度外，在完成模型預(yù)測(cè)所花費(fèi)的時(shí)間上同樣極具優(yōu)勢(shì)，表現(xiàn)出高效預(yù)測(cè)性能。圖6給出了所有模型在3個(gè)DMA中完成預(yù)測(cè)范圍24 h，預(yù)測(cè)頻率15 min的需水量預(yù)測(cè)的平均時(shí)間柱狀圖，可見(jiàn)作為耗時(shí)最短的KELM模型在添加修正模塊后，盡管其時(shí)間消耗有所提高，但KELM+FS仍然比目前廣為應(yīng)用的ANN和SVR模型快了大約10倍，這一點(diǎn)使得該模型在需要同時(shí)對(duì)大量用戶進(jìn)行預(yù)測(cè)的情況下仍然具有難以忽視的實(shí)際應(yīng)用潛力。

圖6 各模型計(jì)算所需平均時(shí)間柱狀圖Fig.6 Bar chart of the average time required for each model

4 結(jié) 論

1)對(duì)短期需水量進(jìn)行預(yù)測(cè)時(shí)，KELM模型計(jì)算精度與ANN模型、SVR模型相近(相對(duì)誤差1.8%～5.5%)，但KELM預(yù)測(cè)模型的建模時(shí)間為ANN、SVR模型建模時(shí)間的5%左右；相比極限學(xué)習(xí)機(jī)模型(ELM)，KELM的預(yù)測(cè)性能更加穩(wěn)定。

2)KELM模型具有較好的泛化能力，能夠高效地實(shí)現(xiàn)連續(xù)日用水量預(yù)測(cè)，對(duì)工作日與休息日的用水量預(yù)測(cè)結(jié)果均達(dá)到較高的精度。

3)核極限學(xué)習(xí)機(jī)模型與傅里葉級(jí)數(shù)殘差修正模塊構(gòu)成的組合預(yù)測(cè)模型KELM+FS，可以在不顯著增加預(yù)測(cè)時(shí)間的前提下，提高KELM預(yù)測(cè)模型的精度。