管單元用于縮減巖體滲透張量計算規模

王俊奇，劉博偉，岳 瀟

(1.華北電力大學 水利與水電工程學院，北京 102206；2.山東電力工程咨詢院有限公司，濟南 250014)

裂隙巖體滲流是導致水利、土木工程事故的主要原因之一[1-2]，還關系到采油、核廢料污染的防治、煤田瓦斯危害的防治和填埋垃圾的污水下滲等方面，工程中需要進行細致的考察和分析。

常用的裂隙巖體滲流分析數學模型有離散裂隙網絡模型、等效連續介質模型、雙重介質模型以及混合滲流模型[3]。因滲流主要在裂隙網絡內發生，用離散裂隙網絡模型來模擬巖體滲流規律時精度較高，并且由于離散型裂隙網絡模型忽略了巖塊本身的孔隙系統及裂隙巖體之間的水交替過程，分析時更加簡便。二維離散裂隙網絡模型由于構造簡單發展較為成熟，但計算結果和實際情況相比誤差較大。三維離散型裂隙網絡模型方面，李新強等[4]使用邊界元法計算裂隙網絡的滲透張量，并與有限元法流量分析結果比較驗證方法的有效性。于青春等[5-7]基于管單元模型通過對裂隙網絡的滲透張量進行求解來分析巖體的滲流情況，Ren等[8]提出用統一管網法對裂隙巖體內的滲流情況進行研究，Sun等[9]用3D統一管網法模擬含裂隙的多孔巖石中的裂隙情況。Wang等[6-10]從滲透張量的角度對裂隙網絡的REV尺寸進行研究。王振偉等[11]通過巖體的滲透張量來確定滲流的REV尺寸，并研究了裂隙的密度和跡長對裂隙巖體的滲透張量和REV大小的影響。也有研究發現巖體裂隙存在優勢水力路徑，Zhao等[12-13]發現在裂隙巖體中只有10%～20%的裂隙可以發生滲流，更多的裂隙僅起到存水或持水的作用。Zhang等[14-15]利用數值分析方法以及現場試驗測試進行滲流分析，對特定巖體中優勢水流的形成機理及其路徑進行了相關研究，林宏奕[16]利用質點追蹤技術來對巖體裂隙中存在的優勢水流路徑進行分析，劉華梅等[17]通過對裂隙網絡滲流路徑進行優化，發現剔除對滲流無貢獻的裂隙，可以減少計算量和縮短計算時長，倪紹虎等[18-19]通過對裂隙巖體的滲透特性進行研究發現在裂隙巖體中的滲流的確存在優勢水力路徑。另外，也有一些學者采用不同的方法對砂巖油藏中優勢滲流通道進行識別和分析，如雷霆等[20]提出改進的CRM模型結合生產動態數據來對優勢滲透通道進行識別描述。現有研究工作表明，確定滲透張量方面，一維管單元模型可以顯著縮減計算工作量，而且由于巖體中存在較大裂隙，溝通巖體范圍較大，一定程度也起到優勢水力路徑作用，因此，在確定滲透張量時，一定程度上可以忽略掉連通范圍小的裂隙，但縮減的幅度沒有相關研究。

本研究采用三維裂隙網絡模型對巖體裂隙滲流進行分析，根據巖體露頭裂隙統計參數，用蒙特卡羅法生成巖體的圓盤裂隙網絡樣本，將滲流通道簡化為管單元模型。一定程度上，巖體主干裂隙控制滲透性能，通過對裂隙規模的研究，探索不同縮減規模對滲透張量和巖體REV大小的影響，以及計算規模可縮減的幅度，并通過實際工程案例對此方法進行了驗證。

1 三維裂隙網絡生成與滲透張量求解

1.1 模型的建立與參數生成

采用Baecher模型[21]，建立離散網絡模型時采用三維整體坐標系，將生成的所有裂隙通過該坐標系確定。將坐標系的主軸方向與地理位置一一對應，即X軸正半軸指向東，Y軸正半軸指向北，Z軸正半軸的方向指向上(與高程一致)，按照右手法則來進行方向的角度旋轉。生成裂隙所需要確定的幾何參數包括裂隙的方向(傾向α,傾角β)、大小(半徑r)、位置(圓盤中心點坐標)、隙寬b，即(α,β,r,x,y,z,b)，每個參數變量的生成都遵循其自身的概率密度函數，利用積分法產生隨機變量。

裂隙的位置用裂隙面上有代表性的點來描述，在統計過程中用裂隙圓盤圓心來確定裂隙在空間中的位置，在三維空間中即圓心點(x,y,z)。假設圓心點在研究域各處出現的概率是相等的，即裂隙圓盤中心點的生成服從均勻分布。在生成裂隙網絡時，應先確定生成域的大小，記錄圓心在該生成域內的所有裂隙，然后在生成域內再創建一定范圍內的研究域，記錄圓心在該研究域內的所有裂隙和與研究域邊界相交的裂隙。

生成裂隙三維裂隙網絡后，求出各圓盤的交線，傳統方法是在此基礎上對裂隙圓盤剖分成平面單元進行裂隙網絡水力學分析，但是一個研究域的裂隙多達上萬條，用平面單元分析會產生十幾萬的自由度，使求解效率低下。為簡化分析計算過程，Tsang[22]和Cacas等[23]提出水流在裂隙面內以溝槽流形態運動，因此，可以對裂隙滲流的分析計算進行簡化，如圖1所示。張有天[1]認為可以用一維管單元進行三維裂隙網絡水力學分析。具體簡化模型為將相交裂隙節理圓盤的圓心和交線中心相互連接起來，然后生成管單元，只在管單元內產生水流，圓心與交線的中點即為節點。對于滲流區域內所有節點建立有限元方程組，用矩陣表示為

圖1 三維裂隙網絡簡化分析概念簡圖Fig.1 Conceptual simplified analysis diagram of 3D fracture network

KH=Q

(1)

式中：K為總滲透矩陣，在三維空間中有9個分量；H為節點水頭矩陣；Q為節點流量矩陣。由于是恒定流，方程可解。

1.2 滲透張量的數值求法

數值求法的基本原理為：在模型的某一相對面施加等水頭邊界，兩個面之間存在一定的水頭差，另外兩對相對面施加變水頭邊界[24](如圖2所示)，滲流邊界的節點水頭分布情況如圖3所示。利用該模型共模擬了3組實驗，第一組實驗中令其中一對相對面施加等水頭，在另外兩對相對面施加變水頭，進行計算并保存相應的計算結果。另外兩組實驗只改變等水頭邊界施加的方向，其他不變。由于對稱性，每組實驗的滲流量只計算6個即可，3組實驗共產生的流量數據為18個。根據滲透張量的定義得[21]

圖2 模型的邊界條件Fig.2 Boundary condition of the model

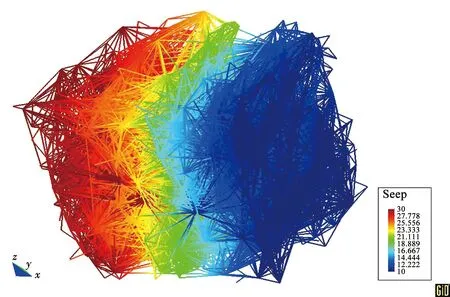
圖3 裂隙網絡滲流水頭分布示意Fig.3 Schematic of seepage head distribution in fracture network

(2)

式中：kij為滲透張量在j方向滲透坡降下產生的i方向分量，qij為滲流量在j方向滲透坡降下產生的i方向分量，ΔPi為在i方向的水力坡降。

對于均質體，在各個方向上的入滲量和出滲量都相等。然而，對于節理巖體，由于巖體中裂隙的分布具有很強的隨機性，巖體的入滲流量和出滲流量并不總是相等。

2 計算規模縮減探索

于青春等[25]研究發現，滲流主要發生在較大的裂隙中，而較小的裂隙對滲流的影響十分微小，因此，在進行裂隙滲流計算時可以在精度允許的情況下將較小的裂隙刪除掉，從而減少計算量，縮短計算時間。本文主要研究了在進行滲流計算時可縮減的規模及其相應的誤差，并用實際工程進行了驗證，當然在實際工程設計中，應根據工程的精度要求選擇合適的縮減量。在此約定：縮減規模為0.1即先將滲流裂隙網絡中的裂隙直徑按照由小到大的順序進行排列，然后去掉排在前1/10直徑的裂隙，只用剩下的裂隙來進行計算。

規模的縮減一般為全排列縮減，即對裂隙網絡空間內所有組數的裂隙從小到大進行整體的規模縮減。例如,若縮減規模為0.1，則將3組裂隙從小到大排列，刪除排在前10%的裂隙，保留剩下的90%進行計算。全排列縮減方式的弊端在于容易較多地刪除直徑最小的那組裂隙，可能會降低滲透張量的準確性。考慮到力學成因，此組裂隙可能開度較大，滲透能力并不弱，因此，提出另一種縮減方法，即對各組裂隙按指標分別從小到大規模縮減，例如,若縮減規模為0.1，分別對每組裂隙從小到大排列，再分別刪除每組前10%的裂隙，然后將各組的剩余裂隙重新統計在一起，進行滲透張量計算。該方法在計算滲透張量前保證了各組裂隙縮減的平衡性，使各組裂隙數量均勻縮減。

三維裂隙網絡的參數信息采用李新強等[4]研究的三維裂隙網絡滲流模型，如表1所示，在該區域共產生的裂隙組數為3。

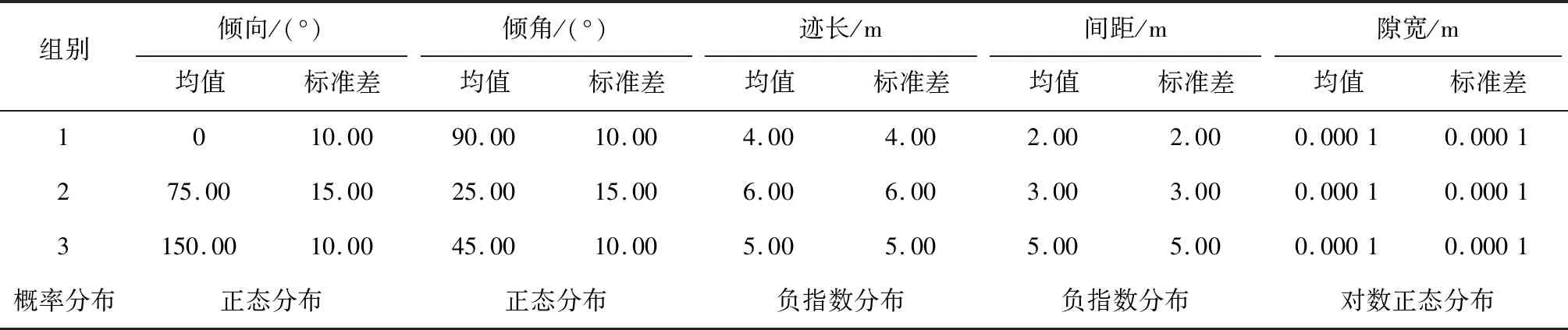
表1 三維裂隙網絡模型參數Tab.1 Model parameters of 3D fracture network

由邊界元法計算確定初值，再用現場壓水試驗校核得到滲透主系數(m/s)和滲透主方向為[4]

(3)

應用自編的C++有限元滲流程序，控制管徑與隙寬的比值為11.506 9[26]，應用上述數據進行滲流模擬，選取100 m×100 m×100 m的立方體區域作為生成域，在生成域的中心選擇20 m×20 m×20 m的立方體作為研究域。對生成的裂隙進行如上所述兩種方式的規模縮減，表2為每組裂隙分別按相同比例的規模縮減，表3為3組裂隙全排列情況下的規模縮減。表2和表3中滲透主值的誤差為

(4)

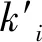
表2和表3中滲透主方向的誤差不可以直接求出，將計算所得滲透主值方向與現場壓水試驗主值方向的夾角作為主方向的絕對誤差。兩滲透主值方向的夾角余弦為

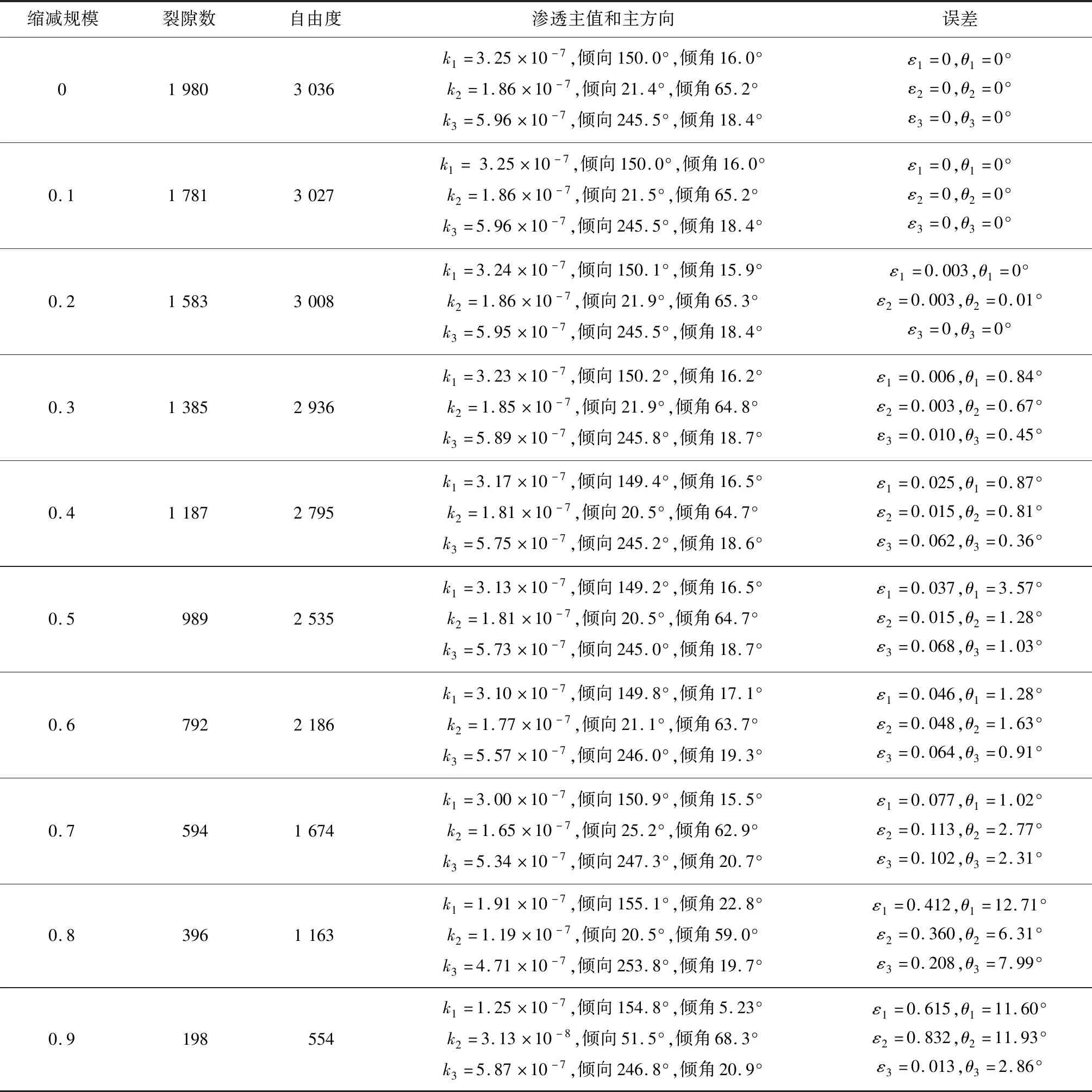
表2 每組裂隙分別按相同比例的規模縮減及相應誤差Tab.2 Scale reduction of each fracture group according to the same proportion and corresponding errors

表3 3組裂隙全排列規模縮減及相應誤差Tab.3 Scale reduction of three fracture groups with full arrangement and corresponding errors

(5)

將未縮減時所得到的滲透主系數和滲透主方向與式(3)進行比較，相應的誤差如下：

(6)

式中：εi為主值相對誤差，θi為主方向絕對誤差，i=1,2,3。

由式(6)模擬可見,模擬計算的結果與現場壓水試驗校正結果的誤差并不太大，在工程實踐可接受的范圍內。

為了便于比較兩種排列方式對滲透張量的影響，將表2和表3中數據分別繪制兩種方式的滲透主值和滲透主方向的誤差圖像，結果如圖4和圖5所示。

圖4 兩種縮減方式滲透主值相對誤差對比Fig.4 Comparison of relative errors of principal permeability for two scale reduction methods

圖5 兩種縮減方式滲透主方向絕對誤差對比Fig.5 Comparison of absolute errors of permeability directions for two scale reduction methods

由圖4可知，兩種縮減方式滲透主值誤差在縮減規模0.1～0.7基本一致。當縮減規模達到0.8時，分組排列的誤差絕對值為11%，全排列的誤差絕對值為9.7%。當縮減規模達到0.8以后，誤差絕對值開始驟然增大，分組排列的誤差絕對值為32.6%，全排列的誤差絕對值為41.3%，此時縮減效果已成病態，不適宜再縮減裂隙規模進行計算。同樣根據圖5可知，兩種縮減方式滲透主方向均值在縮減規模0.1～0.7波動較小。當縮減規模達到0.7以后，分組排列的角度誤差絕對值為2.03°，全排列的誤差絕對值為2.60°。當縮減規模達到0.8以后，誤差絕對值增幅增大，此時分組排列的誤差絕對值為9°，全排列的誤差絕對值為4.9°，此時方向誤差已經不夠準確，不適宜再縮減裂隙規模進行計算。

綜上，對于兩種縮減方式效果基本一致，實際工程中可以采用任意一種縮減方式。當最大縮減規模為0.7時，最為適宜本例，當縮減規模大于0.7時，裂隙滲流網絡中重要的裂隙將被刪除，導致滲流分析的結果與裂隙巖體的實際滲流情況差別較大。

3 巖體表征單元體(REV)的確定

由于在天然巖體中存在的裂隙是隨機分布的，國內外學者在進行巖體力學參數選取時經常會對巖體的表征單元體(REV)進行分析。巖體的各項等效參數具有十分明顯的尺寸效應，當巖體的試樣體積增加到一定值V0時，各項滲透參數趨于穩定，這一V0稱為巖體滲透性代表單元體積(REV)，確定巖體REV的尺寸是進行裂隙滲流研究的一個重要方面。目前，國內外學者對于REV尺寸有從等效力學參數進行分析確定的，也有從水力學參數方面對REV進行研究的，還有從裂隙塊體幾何參數對巖體的REV進行研究的。基于不同巖體參數的尺寸效應而得到的表征單元體的尺寸都不太相同，周創兵等[27]提出了3種確定巖體REV的方法，即數值模擬法、地質統計法和能量疊加法。

本研究運用數值模擬的方法來計算巖體的滲透張量，根據滲透張量3個滲透主系數的變化情況來確定巖體的REV尺寸，通過對不同縮減規模情況下裂隙網絡REV的研究，進一步探索規模縮減對裂隙巖體REV的影響。在縮減規模確定的情況下，對研究域從9 m×9 m×9 m開始逐漸增加到23 m×23 m×23 m，每次研究域的邊長增加1 m。以計算規模未進行縮減時的情況為例，管徑與隙寬的比值為11.506 9，控制生成域的大小為100 m×100 m×100 m，通過不斷改變研究域的大小，得到不同研究域的滲透張量，將所得的裂隙網絡滲透主系數繪制成折線圖，如圖6所示。可以看出，當所生成的裂隙網絡研究域的邊長增大到15 m后，隨著研究域邊長的增大，巖體滲透張量的滲透主系數變化情況基本趨于穩定，故當縮減規模為0時的REV尺寸可取15 m×15 m×15 m。同理，對其他縮減規模下的REV尺寸進行分析，并將得到的REV的邊長繪制在折線圖上，如圖7所示。可以看出，隨著裂隙網絡縮減規模數值的增大，巖體的REV尺寸逐漸變大，說明裂隙密度對巖體的表征單元體大小有一定的影響，REV尺寸隨裂隙密度減小而增大，該認識與李錦輝等[28]對裂隙數量與REV尺寸關系[11]的研究結論相一致。

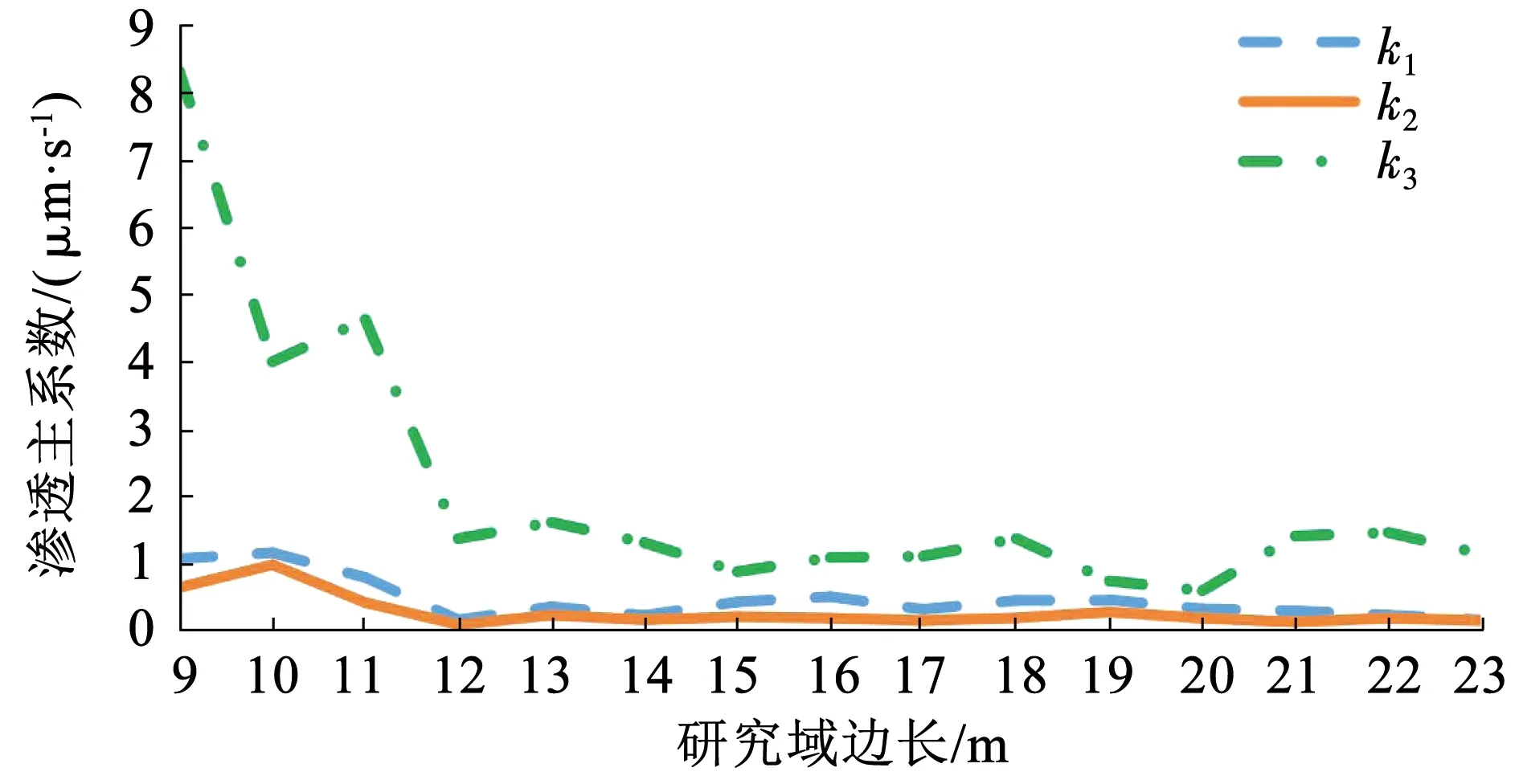
圖6 計算規模不縮減時的滲透主系數Fig.6 Principal permeability curves without calculation scale reduction

圖7 不同縮減規模下的REV邊長Fig.7 REV side lengths for different scale reductions

4 工程驗證

中國水利水電科學研究院的科研人員在新疆對某水利樞紐的左岸邊坡巖體進行現場調研后，根據巖體中結構面的分布和組合情況得到如表4所示的統計結果[29]。

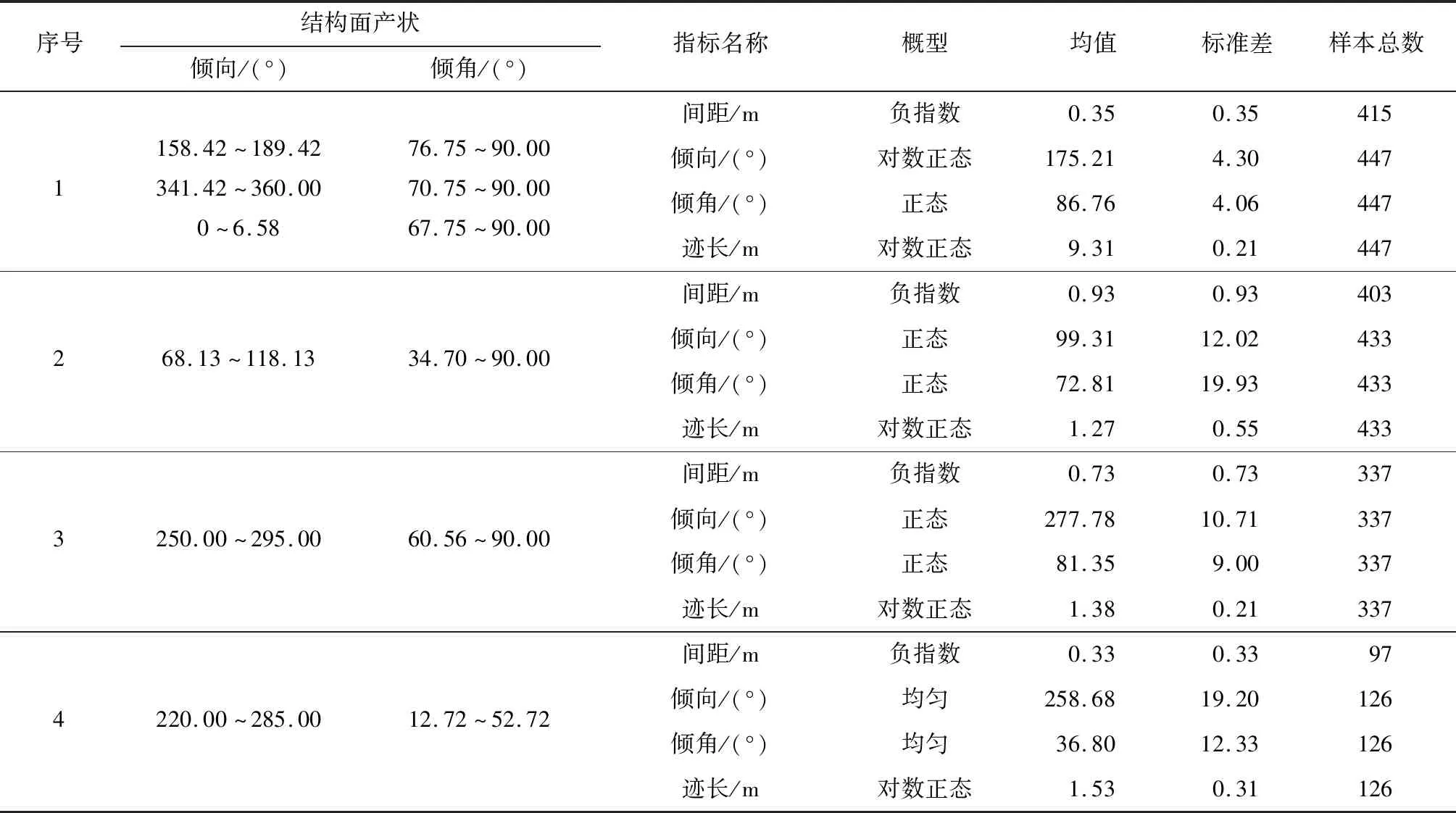
表4 巖體結構面幾何參數統計結果Tab.4 Statistical results of geometric parameters of rock mass structural surface

對此工程實例，用自編的程序進行數值模擬，將生成域的大小設為40 m×40 m×40 m，研究域的大小為15 m×15 m×15 m。不縮減時在生成的研究域內裂隙共有8 129條，在裂隙網絡中節點數為53 650，單元數為99 659，經過數值仿真模擬得到相應的滲透主系數及滲透主方向為

(7)

本工程實例采用縮減規模為0.7，經縮減后共剩2 394條裂隙，在裂隙網絡中共有15 986個節點、29 716個單元，經數值仿真模擬得到相對應的滲透主系數及滲透主方向為

(8)

為形象化滲透特性,根據滲透橢球方程

(9)

將式(7)、(8)用MATLAB軟件繪制縮減前后的滲透橢球圖，如圖8所示,由于橢球具有對稱性，為更好地顯示，取橢球的一半進行觀察。

圖8 縮減前后滲透橢球對比Fig.8 Comparison of permeability ellipsoid before and after reduction

由式(7)和(8)對比及圖8可以看出，縮減前與縮減規模為0.7的滲透張量及滲透橢球相差不大，說明采用縮減規模為0.7時，計算出的滲透主系數和滲透主方向與未縮減前計算的結果比較接近，這一方法對于工程實際具有一定的參考價值。

對縮減前后裂隙巖體模型的REV尺寸進行計算得：

1)未縮減時裂隙巖體的REV邊長為4 m，相應的滲透主系數和滲透主方向為

(10)

2)縮減規模為0.7時的REV邊長為6 m，相應的滲透主系數及滲透主方向為

(11)

將式(11)與(10)進行比較，滲透主系數及滲透主方向的誤差分別為

(12)

式中:εi為主值相對誤差，θi為主方向絕對誤差，i=1,2,3。

由式(12)可知，未縮減時邊長為4 m的REV與縮減為0.7時邊長為6 m的REV滲透主系數相對誤差的最大值為0.257，滲透主方向絕對誤差的最大值為4.62°，縮減前后REV的滲透主系數和滲透主方向誤差均較小。

5 結 論

1)通過刪減次要裂隙、保留主干裂隙進行滲透張量計算，結果表明，裂隙網絡確實存在優勢路徑，保留主干裂隙、縮減計算規模0.7時，計算得到的滲透張量仍然具有較好的精度，可以滿足工程需要。

2)對全排列和分組排列兩種方法的規模縮減程度與結果精度進行分析，裂隙的滲透主值與主方向與現場壓水試驗校核后的結果誤差在可以接受的范圍內，而且兩種方法的縮減效果基本一致。

3)裂隙巖體REV尺寸的大小會隨著縮減規模的增大而變大，通過對巖體表征單元體的討論，發現縮減規模從0變化到0.7時，裂隙巖體的REV體積由15 m×15 m×15 m逐漸增大到21 m×21 m×21 m，說明REV的尺寸受縮減規模的影響。工程實例REV的邊長隨著縮減規模的增加從4 m增大到了6 m。

4)通過實例驗證縮減計算的實用性。巖體裂隙網絡滲流滿足逾滲條件，存在REV情況下，對于那些對精度要求不高、地質條件不復雜的情況，滲透張量可以采用縮減規模數為0.7進行計算。對于工程精度要求較高、地質條件復雜的重要工程項目，應結合現場的實測資料與試驗，選擇合適的縮減規模數進行分析。在誤差允許的條件下相對地減少最大縮減量，可以達到減少計算量的目的，提高三維裂隙離散網絡模型在工程中的實用性。