基于快速多極子邊界元法的齒輪箱聲場分析

劉學良，馮治恒，吳海軍，莫 蓉

（1.上海交通大學機械系統與振動國家重點實驗室，上海 200240；2.廣西柳工機械股份有限公司，廣西柳州 545007）

0 引 言

齒輪箱在工程機械中非常重要，主要用于發動機動力輸入、扭矩輸出至軸系等方面。現今齒輪箱的輻射噪聲越來越受到重視[1-2]，其不僅會產生環境的噪聲污染問題，還會影響減速器的正常工作，降低設備的疲勞壽命。因此，準確地計算齒輪箱的輻射噪聲，對其進行噪聲評估以及低噪聲優化有著重要的意義。隨著傳動技術的提升，如何在高轉速、大功率、大扭矩的齒輪箱中降低振動和輻射噪聲，是工程設計中的嚴峻課題[3]，同時也對噪聲預測提出了更高的要求。

齒輪箱的噪聲預測方法有統計能量分析（Statistical Energy Analysis,SEA）、有限元法（Finite Element Method,FEM）、邊界元法（Boundary Element Method,BEM）[4]等多種方法，其中BEM是一種基于積分方程的計算方法[5]。邊界元方法僅需對模型邊界進行離散，并且求解精度較高，能自動滿足無限遠處的 Sommerfeld輻射條件，因而非常適用于分析自由空間下的聲傳播問題[6]。因此本文選用邊界元方法對齒輪箱進行聲場分析。目前國內外關于邊界元法在齒輪箱聲場的噪聲預測有一定的研究。王勝男等[7]運用邊界元法分析了二級齒輪箱的輻射噪聲；焦映厚等[8]建立了大型立式齒輪箱的外聲場邊界元模型并分析了輻射聲場；Le Moyne等[9]用邊界元法分析了齒輪箱的加筋板對聲輻射的影響。但以上研究所采用的均為傳統邊界元方法（Conventional Boundary Element Method,CBEM）。CBEM存在著求解效率低、內存占用大的固有缺陷[10]，無法用于大規模聲學問題的計算。而齒輪箱在不同工況下的噪聲頻譜一般比較寬，在寬頻段內的掃頻分析更加耗時，不利于產品聲學設計的及時評估及優化設計。因此需要考慮加速算法。而快速多極子的方法出現，將邊界元方法的計算量和存儲量降低到O（N）量級，其中N為計算模型的自由度，從而使邊界元方法在求解大規模聲學問題上得到了迅速發展[11]。

本文發展了寬頻快速多極子邊界元算法，并運用了多核并行方法加速計算，克服了以往傳統邊界元方法求解效率低、內存占用大的缺點。通過對工程中的某齒輪箱進行建模以及有限元仿真，得到模型表面節點的振速信息。再運用所發展的快速多極子邊界元方法對齒輪箱進行輻射聲場分析以及掃頻計算，大幅度地降低了求解時間，為后續的低噪聲優化設計提供了理論依據。

1 邊界元法理論

在均勻理想介質中，線性聲學波動方程[12]為

可以得到傳統邊界積分方程（Conventional Boundary Integral Equation,CBIE）為

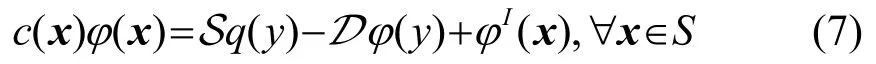
可以得到相應的超奇異邊界積分方程（Hypersingular Boundary Integral Equation,HBIE）為

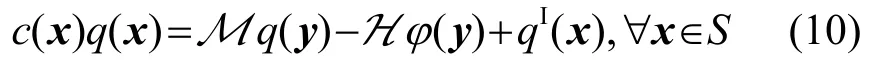
2 數值算法實現

2.1 邊界元法數值實現

如前所述，將式（7）、（10）進行線性組合，得到的Burton-Miller方程為

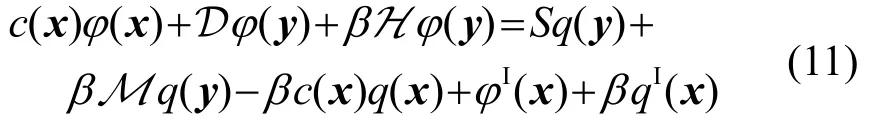
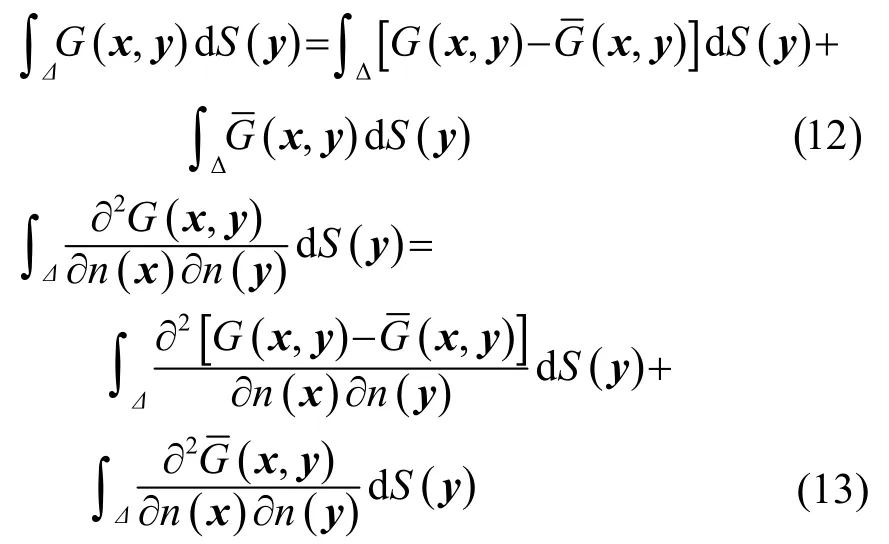
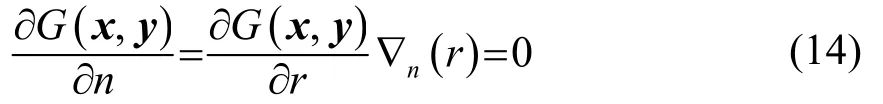
采用三角形或者四邊形常數單元進行離散，并代入已知邊界條件，將未知邊界量及其系數重組，最終可以生成方程：

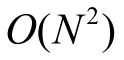
2.2 快速多極子方法

快速多極子方法[18-20]在20世紀80年代提出。該方法的引入，極大地降低了邊界元法的求解時間和內存占用量，推動了邊界元法的快速發展。快速多極子方法的核心思想是Green函數在高頻下的平面波展開和低頻下的級數展開。通過將源點對場點的貢獻進行分塊層級傳遞，達到降低計算量的目的。以高頻為例，其平面波展開形式為：

其中：x為場點；y為源點；k為波數；xc是本地系數展開中心；yc是源點矩的匯聚中心；為球面上的法向量；為向量的模，快速算法的具體步驟如圖1所示。

首先，通過模型離散和算法實現，生成樹狀結構。其次，通過上行、下行計算兩個步驟計算b向量，上行計算主要為各個柵格的源點矩計算，其公式為

其中，M為源點矩，yc為樹結構中柵格的中心點。下行運算主要為源點矩轉移（M2M）、源點矩到本地展開系數傳遞（M2L）及本地展開系數轉移（L2L）。通過層級傳遞，最終計算得到源點對場點的貢獻。本文通過運用快速多極子算法，最終完成了低頻、高頻的快速多極子邊界元方法，并將兩者結合，最終發展了寬頻的快速多極子邊界元方法。

圖1 快速多極子算法流程圖Fig.1 The flowchart of fast multipole method

3 齒輪箱模型處理

3.1 齒輪箱模型

首先建立齒輪箱的幾何模型，建模過程中需要對模型進行合理簡化，略去較小的倒角和其他細小特征。通過建立齒輪-軸-軸承系統的耦合動力學模型，對齒輪箱進行動力學分析，得到齒輪箱的載荷，并運用有限元法計算齒輪箱的各階模態。其次，對齒輪箱進行頻段為4～2 000 Hz、步長4 Hz的諧響應分析，計算得到各頻率下齒輪箱表面的節點振速信息，作為邊界元法的輸入邊界條件。

邊界元模型是結構有限元模型的外輪廓，運用商用軟件對有限元模型進行網格處理，提取得到齒輪箱輪廓的網格模型如圖2所示，其模型參數見表1所示。

3.2 邊界條件處理

邊界元方法只需要模型表面輪廓的邊界條件。將有限元分析所得到的各頻率下的齒輪箱表面的節點振速進行分析處理，可以得到離散面單元的聲壓法向導數，并將其作為邊界條件。其中節點聲壓的法向導數與振速V的關系為

圖2 三角形單元劃分的模型Fig.2 The model divided with constant triangular elements

表1 齒輪箱模型參數Table 1 The parameters of gear box model

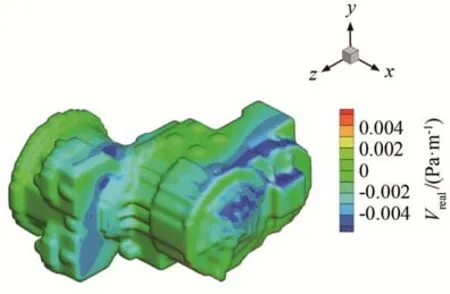
圖3 邊界條件實部云圖Fig.3 Nephogram of the real part of boundary condition

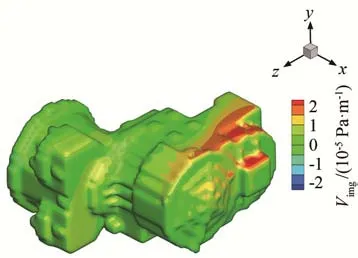
圖4 邊界條件虛部云圖Fig.4 Nephogram of the imaginary part of boundary condition

4 齒輪箱聲場分析

本節介紹齒輪箱的聲場分析結果，分別計算了頻率為 100 Hz時的場點聲壓、齒輪箱的輻射聲場以及4～2 000 Hz的掃頻分析。計算所用的計算機主要參數如表2所示。

表2 計算機配置參數Table 2 The configuration parameters of computer

4.1 場點計算

為了驗證預測結果的正確性，如圖 5所示位置布置場點，計算頻率為 100 Hz時的場點聲壓以及齒輪箱邊界聲壓。

圖5 場點分布Fig.5 The distribution of field points

運用快速多極子邊界元方法，可以計算得到全空間下齒輪箱表面的聲場，其結果如圖6、圖7所示。

為了驗證加速算法的計算精度和效率，對比了快速多極子邊界元法與某商用軟件的計算結果。商用軟件和快速邊界元方法在計算參數上的對比如表3所示。快速算法和商用軟件的場點計算結果對比見圖8所示。

從圖8中可以看出，算法與商用軟件的計算結果較為接近。

圖6 聲場實部計算結果Fig.6 Nephogram of the computational results of real part of the sound field

圖7 聲場虛部計算結果Fig.7 Nephogram of the computational results of imaginary part of the sound field

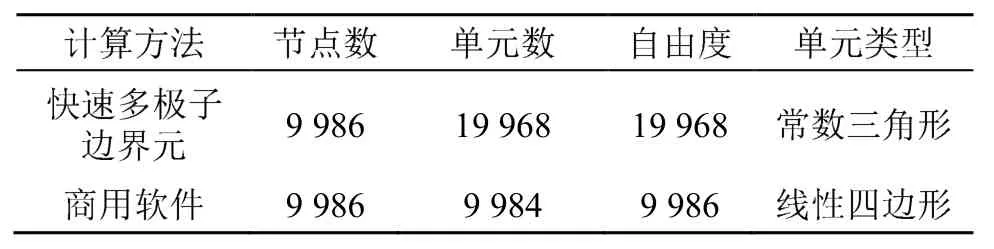
表3 快速算法和商用軟件計算參數對比Table 3 The comparison of parameters between the fast algorithm and the commercial software

圖8 快速算法和商用軟件的聲場計算結果對比Fig.8 Comparison of sound field computational results between the fast algorithm and the commercial software

4.2 齒輪箱輻射聲場計算

該部分通過計算齒輪箱附近的場點，得到頻率為 100 Hz時的齒輪箱輻射聲場。其場點模型如圖9所示。

圖9 場點模型Fig.9 The model of field points

圓環模型的圓心坐標為（0,0,0.75）m，內徑為1.2 m，外徑為 4.8 m，共有 3 202個場點，6 153個單元。運用快速多極子邊界元方法進行求解，得到其在100 Hz時的輻射聲場如圖10、11所示。

圖10 齒輪箱輻射聲場實部Fig.10 Nephogram of the real part of radiation sound field of the gearbox

圖11 齒輪箱輻射聲場虛部Fig.11 Nephogram of the imaginary part of radiation sound field of the gearbox

從云圖中可以清楚地看到齒輪箱周圍的聲場分布，進而為齒輪箱后期的降噪處理和低噪聲設計提供理論依據。

4.3 齒輪箱掃頻計算

該部分對齒輪箱進行掃頻計算，計算頻率為4～2 000 Hz，步長為4 Hz，共500步。首先對數據進行處理，得到500步中每一步的邊界條件，最終得到包含500步的邊界條件文件。將邊界條件代入快速算法進行計算，得到掃頻計算結果。最終處理數據，得到每一個場點的聲壓級LSP，其計算公式為

從圖12中可以看到，商用軟件和快速邊界元方法的掃頻結果趨勢相近，在個別頻率處的計算結果有差異。該差異由算法的方法差異所決定，快速邊界元方法采用了常數三角形單元進行模型離散，而商用軟件采用的是四邊形線性單元進行離散。從理論上講，相同自由度下，線性單元的計算精度略高于常數單元。而在目前齒輪箱的模型中，快速多極子邊界元模型的自由度為商用軟件所采用模型自由度的2倍，由此分析，理論上快速邊界元的計算結果應該更為準確一些。

此外，運用多核并行計算對掃頻分析進行加速，最終得到快速多極子邊界元方法的計算時間如表4所示。

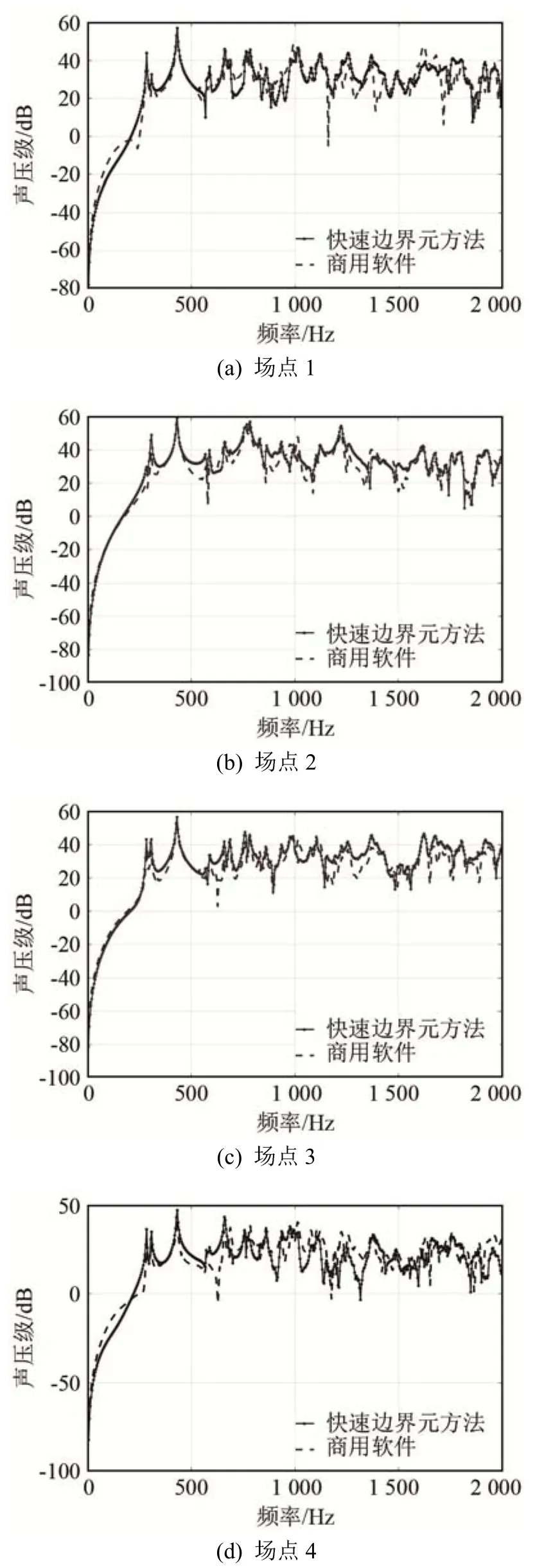
圖12 商用軟件和FM-BEM掃頻計算得到的4個典型場點的聲壓譜比較Fig.12 Comparison of the sound pressure spectrums obtained by the frequency sweeping calculations of commercial software and FM-BEM at four typical field points

表4 快速多極子邊界元方法計算時間Table 4 The computation time of FM-BEM

從表4中的數據可以看到，運用多核并行計算可以加倍提升計算效率。當采用36核進行計算時，共500步的掃頻計算僅需2 h 15 min，大大提高了計算效率。采用多核并行計算的快速多極子邊界元方法為齒輪箱噪聲預測提供了強大的算力支撐。

5 結 論

本文運用快速多極子邊界元方法，通過對齒輪箱輻射聲場的系統分析，得到了齒輪箱的聲場分布、單頻處的場點聲壓以及掃頻聲壓。通過對比商用軟件，驗證了該快速多極子邊界元方法的準確性。此外，通過運用多核并行計算，進一步加快了計算速度，最終快速完成了齒輪箱的掃頻分析，為后續的低噪聲優化設計提供了充分的理論依據。