基于偏最小二乘回歸算法的空氣質量監測系統研究*

王 剛， 張福印， 李明輝， 王金龍， 王藝博， 武傳偉

(1.漢威科技集團股份有限公司，河南 鄭州 450001；2.鄭州大學 化工學院，河南 鄭州 450001)

0 引 言

隨著我國國民經濟不斷發展和城市化進程的加快，大量工業廢氣、工地揚塵以及化石燃料燃燒產生的污染物排放到大氣中，造成嚴重的空氣污染，制約著經濟的可持續綠色發展。近年來，顆粒物污染和臭氧污染已成為影響我國城市空氣質量的關鍵因素之一[1]。隨著大氣污染防治工作逐漸向區縣、園區等精細尺度延伸，網格化高密度監測的需求逐漸旺盛[2]。針對該需求，利用低成本多參數空氣質量監測系統或標準儀器監測系統通過密集布點的模式，可以獲得更高時空分辨率的污染分布特征，實現對環境氣體的實時精確監測[3]。

低成本多參數空氣質量監測系統與標準儀器監測系統相比，具有價格低廉、體積小等優點，然而，由于傳感器與標準儀器之間的對比工作還不夠完善，對于具體的用戶來說，傳感器數據的可信度有待考證。另外，網格化布設的多參數空氣質量監測系統大多工作在室外，環境因素是一個影響很大的變量，進而導致傳感器在室外測試中的效果往往不太理想[3]。算法優化使得數據訂正結果得到明顯改善[4～8]，也為低成本多參數空氣質量監測系統的性能改善提供了參考。當前，常用的非線性多項式模型補償技術只研究了單一參數，沒有直接應用于多參數監測系統中；其他的主流建模方法還包括神經網絡法，如反向傳播(BP)神經網絡[4]、模糊神經網絡[9]，雖然獲得了較好的效果，但是仍然存在學習速度慢，容易陷入局部最優解及在不同場合參數調整復雜等缺點。

為解決上述問題，本文搭建了一種基于偏最小二乘回歸(partial least squares regression，PLSR)算法的低成本多參數空氣質量監測系統；通過采集得到的顆粒物、氮氧化物(NO2)、二氧化硫(SO2)、臭氧(O3)和一氧化碳(CO)等傳感器模組原始信息，及標準設備的相關濃度信息，分別建立PLSR模型，并對模型的參數估計進行逼近，得到最優模型；最后通過放置室外與實測值對比，進行驗證。

1 模型介紹

1.1 PLSR模型和評價方法

PLSR主要用于變量個數較多，而觀測數據數量較少，且變量之間存在多重相關性時的回歸建模[10]。用PLSR建立的模型，可以通過提取成分和篩選成分的方式，提取對因變量的解釋最強、對因變量影響最大的綜合變量，具有傳統經典回歸分析等方面所沒有的優點[10]。PLSR分析可以集成多元線性回歸分析、典型相關分析和主成分分析，可以很好解決變量之間存在多重相關性或樣本點過少的回歸難題。

通過回歸分析，將低成本多參數空氣質量監測系統得到的各個監測因子的數據與標準儀器的數據進行線性擬合，得到決定系數R2，計算公式為

(1)

還可以通過均方根誤差(root mean square error,RMSE)來評價傳感器數據本身的質量

(2)

式中yi,p和yi分別為傳感器第i個數據與標準儀器第i個數據。

模型建立和評價方法可以通過如圖1所示的數據處理流程圖來表示。

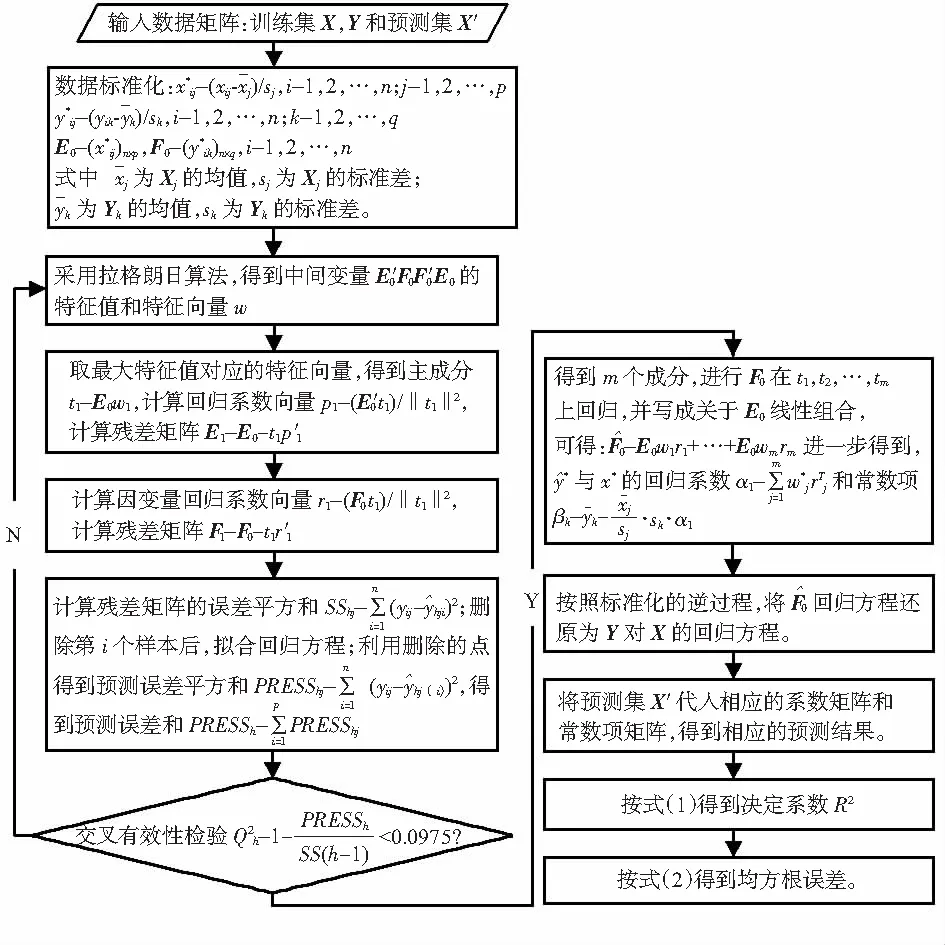
圖1 數據處理流程圖

1.2 顆粒物濃度預測模型建立與分析

本文所采用的顆粒物傳感器，可以同時輸出0.3～10 μm粒徑范圍的顆粒物數量，主要原因是小于0.3 μm的顆粒物不能散射足夠的光強而無法用光度計測量到，而大于10.0 μm的顆粒物由于很難進入光感應區而難以被測量[12]。在本模型中，將不同范圍粒徑數的顆粒物按表1進行分類。將A0.5，A1.0，A2.5，A5.0，A10.0作為PM2.5和PM10濃度貢獻的自變量，PM2.5和PM10.0為因變量，建立PLSR模型，即

表1 顆粒物傳感器粒徑輸出分類

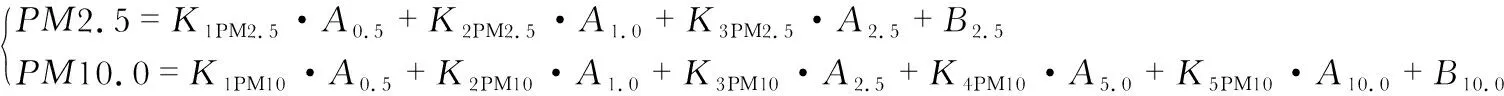
(3)

式中B2.5和B10.0為求解PM2.5和PM10.0濃度時的常數項，K為對應的系數。

1.3 氣體濃度預測模型建立與分析

由于臭氧是一種強氧化性氣體，可以對SO2,NO2產生一定的氧化還原反應。因此，在對氣體濃度建模時，同時考慮三種氣體之間的相互作用。另外，CO也是常規測試的氣體。針對4種氣體的濃度監測模型為

(4)

2 實驗部分與數據來源分析

2.1 系統結構

為了有效支撐模型驗證工作，搭建了一種低成本多參數空氣質量監測系統，其總體框圖如圖2所示。為了盡可能消除外界環境對傳感器的影響，通過采樣頭和伴熱管線提高顆粒物傳感器測量的可靠性；通過采樣泵和恒溫裝置提高SO2NO2O3CO傳感器測量的可靠性。顆粒物傳感器的測量結果通過數據總線傳輸至系統控制模塊；氣體傳感器的輸出與待測物質濃度相關的電信號，通過調理電路轉換成相應的數字信號，再傳輸至系統控制模塊。系統控制模塊把收到的數字信號加以處理，傳輸至顯示模塊，方便本地顯示處理；通過傳輸模塊把本地數據直接上傳至相應的平臺，進行數據二次處理和展示。系統控制模塊，還可以通過伴熱控制模塊和恒溫控制模塊，分別保證伴熱管線和恒溫裝置的溫度穩定性。

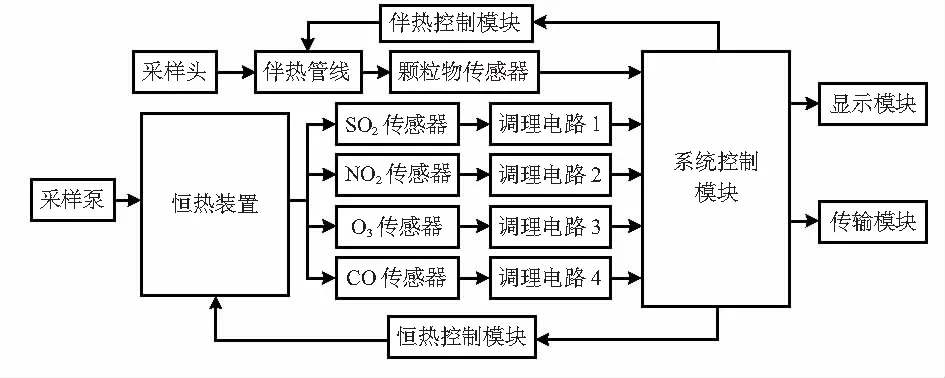
圖2 低成本多參數空氣質量監測系統框圖

本文監測系統中，所使用的顆粒物傳感器是基于光散射原理的，即空氣中的顆粒物進入傳感器之后在激光光源的照射下會發生散射，然后利用光度計來測量顆粒物散射出來的光強，通過從散射光獲得的信號使用算法來對可檢測顆粒進行粒徑分離，轉換成需要的濃度值。所使的NO2,SO2,O3,CO等四個因子傳感器則是基于電化學原理的。

2.2 標準儀器介紹

顆粒物監測的標準儀器，選用的是采用β射線衰減原理的由Thermo Scientific公司生產的5014i型環境顆粒物連續監測儀。環境空氣由采樣泵吸入，經顆粒物切割器后進入采樣，途經自動加熱管，最后沉積在采樣濾膜上。由C—14放射源發出的β粒子在穿過采集了顆粒物的采樣膜后其能量會發生衰減，根據顆粒物吸收β射線的量與粉塵粒子的質量成正比關系來計算出粉塵的質量濃度[12]。NO2監測的標準儀器，選用基于化學發光技術[13]的42i型(NO—NO2—NOx)分析儀，通過將NO2轉化成亞硝酸根，利用還原劑將亞硝酸鹽轉化為NO后與O3反應的氣相化學發光。發光強度與NO2的濃度成線性比例關系。SO2監測的標準儀器，選用基于脈沖熒光技術的43i型SO2分析儀，SO2分子在吸收紫外激勵光后，會躍遷至較高的能量狀態，然后衰減至較低的能量狀態，同時在另一個波長發射出紫外光，所發射的UV光與SO2濃度成正比。O3監測的標準儀器，選用基于朗伯—比爾定律的49i型雙光室紫外光度臭氧分析儀，利用O3濃度對254 nm紫外光吸光度成正比。CO監測的標準儀器，選用的是采用48i型氣體過濾相關法CO分析儀，基于CO對波長4.6 μm的紅外輻射有吸收的原理，且濃度與吸收成正比。

2.3 數據來源

測試數據是2020年12月2日至2020年12月8日采用自研儀器測得的PM2.5,PM10,CO,SO2,NO2,O3數據，及采用標準儀器得到的數據。為了便于對比，多參數空氣質量監測系統和標準設備的時間間隔都是5 min。

3 實驗分析

基于1.2節和1.3節的模型研究，根據式(3)，可建立顆粒物的偏最小二乘模型如式(5)所示

(5)

測得12月2日至12月8日，標準儀器測量結果與低成本多參數空氣質量監測系統的預測結果時序圖如圖3所示。其中MIPM2.5與MIPM10分別表示標準儀器測量的PM2.5和PM10濃度結果；預測PM2.5與預測PM10分別表示低成本多參數空氣質量監測系統測量的PM2.5和PM10濃度結果。可以發現預測結果與標準結果的測量結果差值均小于20 μg/m3。標準設備測量結果與預測結果的均方根誤差分別為11.64 μg/m3和13.35 μg/m3；其決定系數R2如圖4所示，分別為0.838 7和0.803 1。p>

圖3 顆粒物濃度標準儀器測量結果與預測結果的時序

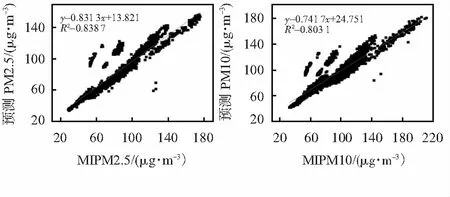
圖4 標準設備測得PM顆粒物濃度和低成本多參數系統測得濃度對比

根據式(3)，可建立四種氣體的偏最小二乘模型如式(6)所示

(6)

測得12月2日至12月8日，標準儀器測量結果與低成本多參數空氣質量監測系統的預測結果時序圖如圖5所示。其中SO2,NO2,CO和O3分別表示標準儀器測量的相應四氣體的濃度結果；預測SO2,預測NO2,預測CO和預測O3分別表示低成本多參數空氣質量監測系統測量的相應四氣體的濃度結果。可以發現預測結果與標準結果的趨勢變化是比較一致的。標準設備測量結果與預測結果的均方根誤差分別為：2.77 μg/m3,15.67 μg/m3,0.11 mg/m3和28.83 mg/m3；其決定系數R2如圖6所示，分別為0.217 8,0.447 9,0.571 5和0.353 7。

圖5 四種氣體濃度標準儀器測量結果與預測結果的時序圖

圖6 標準設備測得氣體污染物濃度和低成本多參數系統測得濃度對比

4 結 論

本文提出了一種低成本多參數空氣質量監測系統，采用偏最小二乘回歸法，建立顆粒物傳感器不同粒徑輸出與顆粒物濃度PM2.5和PM10之間的關系模型；建立氣體傳感器輸出與氣體污染物濃度之間的關系模型。建模過程簡單方便，具有較好的操作性。實驗結果表明，標準設備測量PM2.5和PM10結果與預測結果的均方根誤差分別為11.64 μg/m3和13.35 μg/m3；決定系數R2分別為0.838 7和0.803 1; 標準設備測量SO2,NO2,CO和O3的結果與預測結果的均方根誤差分別為：2.77 μg/m3,15.67 μg/m3,0.11 mg/m3和28.83 μg/m3；其決定系數R2分別為0.217 8,0.447 9,0.571 5和0.353 7。因此，在大氣空氣質量測量中，可使用偏最小二乘回歸法對PM2.5,PM10,SO2,NO2,CO和O3等污染物進行預測，并取得較好的實驗結果，且符合環保產品認證實施規則中微型環境空氣質量監測系統的技術要求。