基于移位內插互質陣列高分辨DOA估計*

曾耀平， 劉 洋

(西安郵電大學 通信與信息工程學院，陜西 西安 710121)

0 引 言

波達方向(direction of arrival,DOA)估計是陣列信號處理的關鍵技術之一，在雷達、通信、衛星導航等都發揮著重要作用[1]。近年來，由于稀疏陣列[2]更大陣列孔徑和自由度，基于稀疏陣列的DOA估計逐漸受到廣泛關注。文獻[3]提出一種嵌套陣列，通過N個陣元最多可獲得o(n2)的陣列自由度，但是互耦效應會影響波達方向估計的結果。文獻[4]提出一種互質陣列，用M+N-1個陣元可獲得o(mn)自由度，但虛擬域的孔洞缺失導致最大可用自由度減少。文獻[5]提出一種虛擬陣列協方差矩陣稀疏重建的DOA估計算法，重構虛擬域協方差矩陣來提高陣列自由度，但算法復雜度略高。文獻[6]研究了基于壓縮感知的互質陣列DOA估計，降低計算復雜度，但非均勻虛擬域中信息缺失以及預定義空間網格點造成估計偏差問題有待解決。文獻[7]提出一種基于互質陣列內插無網格化DOA估計算法，利用了全部接收信號信息，利用所有虛擬陣元，尋找最接近內插虛擬陣列協方差矩陣的協方差矩陣來進行DOA估計。

本文提出一種移位互質陣列虛擬內插的無網格化DOA估計研究，首先對互質陣列改進形成移位互質陣列，其次對虛擬域缺失孔洞填充形成連續虛擬線陣，最后通過原子范數最小化的優化設計和內插虛擬陣列協方差矩陣稀疏重建進行DOA估計。所提出的方法進一步提高陣列孔徑和自由度，解決虛擬域信息缺失和預定義網格點產生的誤差，仿真結果體現了算法的有效性。

1 移位互質陣列與信號模型

簡單互質陣列模型，由一對滿足互質條件的均勻線性陣列以首個陣元重疊的方式構成。設子陣列1有M個陣元，間距是Nd；子陣列2有N個陣元，間距為Md；d=λ/2，共包含M+N-1個陣元如圖1。本文對簡單互質陣列的兩個均勻線陣進行錯位偏移，令陣元數為M的陣列相對于陣列數為N的陣列向后偏移M的整數倍，稱之為移位互質陣列如圖2。通過差集數組擴展到虛擬域，當M+N>7時，互質陣列至少含有MN個虛擬陣元,其中2(M+N-1)+1個連續均勻虛擬陣元，移位互質陣列至少含有MN+M-1個虛擬陣元，其中2(M+N-1)+2M個連續均勻虛擬陣元。在保證陣元個數不變的情況下，移位互質陣列構成的虛擬域中增加了陣元數量，提高陣列自由度。

圖1 互質陣列

圖2 移位互質陣列

假設目標空間有K個目標信號入射到移位互質陣列上，入射信號方位角為θ=[θ1,θ2,…,θk]T，[·]T為轉置操作，則在t時刻接收信號的模型為

(1)

對于第k個入射信號的方向向量a(θk)可以表示為

(2)

(3)

式中pk為第k個入射信號的功率，E[·]為期望，(·)H為共軛轉置操作，理想協方差通常取采樣協方差進行近似代替，則采樣協方差可由采樣快拍數據表示為

(4)

當采樣快拍數在平穩遍歷的情況下趨于無窮時，采樣協方差矩陣趨近于理想協方差矩陣，但是當采樣快拍數受限時，二者之間的差異會影響DOA估計。

2 移位互質陣列虛擬域孔洞填充

為了提升陣列自由度，現將互質陣列和移位互質陣列推廣至虛擬域如圖3、圖4。

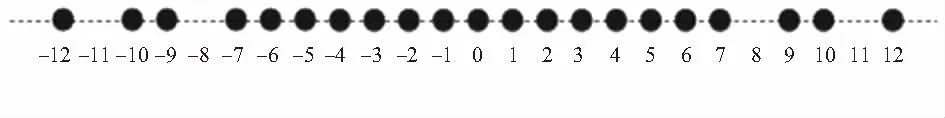
圖3 M=3，N=5的簡單互質陣列的非均勻虛擬陣列

圖4 M=3，N=5的移位互質陣列的非均勻虛擬陣列

虛擬陣列等價信號可以通過向量化接收信號的協方差矩陣R得到

yv=vec(R)=Avp+σ2i

(5)

式中Av=[a*(θ1)?a(θ1),a*(θ2)?a(θ2),…,a*(θk)?a(θk)]∈C(M+N-1)2×K,p=[p1,p2,…,pk]T包含k個入射信號的功率，i=vec(I),?為克羅內克積，vec(·)是對矩陣進行向量化，(·)*為取共軛，Av對應于虛擬陣列的導引向量。其中虛擬陣元位置可以定義為

V={ui-uj|，ui,uj∈S,i,j=0,1,…,M+N-1}

(6)

差集數組中有大量重復元素，非均勻虛擬陣列通過取差集數組中的唯一值得到：Sv?{±(Mn-Nm)|m=0,1,…,M-1,n=0,1,…,N-1}，對應的等價虛擬信號通過選取yv中相對應位置的元素獲得

(7)

一對m=3，n=5的互質整數，物理陣元個數不變的情況下，互質陣列包含21個陣元位置差，其中連續陣元位置差的范圍是[-7,7]，共有15個連續陣元位置差；移位互質陣列包含23個陣元位置差，其中連續陣元位置差的范圍是[-10,10]，共有21個連續陣元位置差。移位互質陣列使虛擬域中陣元個數增加，自由度提高。

以上虛擬陣列均存在若干缺失元素，如果將奈奎斯特采樣定理的統計信號處理方法直接引入非均勻虛擬域中，將會引起信號模型失配[8]。現有普遍做法是僅提取其中一段均勻連續虛擬陣列進行信號處理，將非連續部分丟棄[9]，非連續部分虛擬陣元所包含的有效信息未得到充分利用，導致DOA估計性能出現一定的衰減。為了利用虛擬域的全部有效信息，本文使用矩陣填充的方法，主要針對數據缺失的情況下重建矩陣[10]，具體為在孔洞位置插入虛擬陣元，將內插虛擬陣元視為未工作狀態的天線陣元，將其對應的接受信號初始化為零，內插虛擬陣列初始化為

(8)

因此,得到移位互質陣列虛擬域連續的內插虛擬陣列V如圖5，內插虛擬陣列為包含2(M-1)N+2M+1個虛擬陣元的虛擬均勻線陣。其中有兩種虛擬陣元，一種是原始非連續虛擬陣元，一種是內插虛擬陣元。內插虛擬陣列的等價接收信號yI包含虛擬域的全部有效信息，可用于奈奎斯特采樣限制的統計信號處理，式(8)中假設內插虛擬位置初始信號為0，為了實現有效DOA估計，需要優化方法恢復內插虛擬陣元位置的信號。

圖5 移位互質陣列虛擬內插V

3 重構算法

首先將理想狀態下內插虛擬陣列等價接收信號表示為

yC=ACp

(9)

式中AC=[aC(θ1),aC(θ2),…,aC(θk)]∈C|V|×K為內插虛擬陣列的導引矩陣。

將內插虛擬陣列分成每份含L=(|V+1|)/2個子向量，則理想條件下內插虛擬陣列等價接收信號向量可表示為Y={yc1,y2c,…,ycL}，為了進行連續化參數表示，Y的原子集合可定義為

Ω={ac(θ)eH(θ)|θ∈[-90°,90°]}

(10)

式中e(θ)=[1,e-jπsin(θ),…,e-jπ(L-1)sin(θ)]T為L個虛擬陣列和首個參考虛擬陣列之間的相位偏移，Y的原子范數表示為

‖Y‖=inf{h>0︰Y∈hconv(Ω)}

(11)

式中 conv(Ω)為原子集合的凸包，式(11)中是多采樣理想虛擬信號原子范數的定義，需要做到通過最少的個數的原子對Y進行原子分解。內插虛擬陣列協方差矩陣R(z)為Toeplitz矩陣，矩陣中的所有元素可以通過其首列構造。因此，內插虛擬陣列協方差矩陣R(z)的重構可以轉化為首列向量z的重構[11]。內插協方差矩陣首列z與首個參考虛擬陣列yc1所對應的等價接收信號相同，其原子范數可表示為

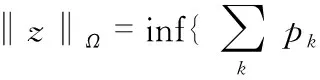
(12)

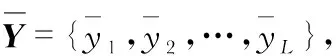
(13)

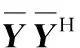
(14)

式中 〈·〉為向量中第l個元素。

通過最小化向量z原子范數的優化來重構內插虛擬陣列的協方差矩陣。需要定義一個二值向量g∈RL區分參考矩陣中的原始陣元與內插陣元，各元素值與參考虛擬陣列中的陣元一一對應，原始陣元對應的值為1，內插陣元對應的值為0。移位內插虛擬虛陣列協方差矩陣Toeplitz重構方法可表示為

subject to‖R(z)

(15)

式中G=ggT∈RL×L為構造的二值矩陣，區分Rv中的內插陣元初始化等價信號和原始非均勻陣列等價信號。為哈達馬積，‖·‖F為Frobenius范數，ε為閾值參數，用于約束擬合誤差。式(15)可用于凸優化問題進行求解，等價表示形式為

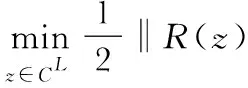
subject toR(z)≥0

(16)

式中ξ為權衡原子范數和擬合誤差的正則化參數。同時原子范數最小化問題可以進一步表示成矩陣求跡最小化問題

subject toR(z)≥0

(17)

μ=ξ/L通過內點法可得到內插虛擬陣列重建的協方差矩陣R(z)。

對移位互質陣列內插協方差矩陣進行特征分解，由于信號子空間和噪聲子空間正交，可采用譜峰搜索進行DOA估計。MUSIC算法的空間譜可以表示為

(18)

本文所提的移位互質陣列虛擬陣元內插的DOA估計算法流程。如下：

1)一對滿足互質條件的均勻線陣；2)移位互質陣列；3)通過式(4)求移位互質陣列采樣協方差陣列；4)通過式(7)移位互質陣列虛擬域等價接收信號；5)通過式(8)內插虛擬陣列信號初始值；6)通過式(9)～式(12)對理想虛擬信號的研究，實現DOA估計連續參數表示；7)通過式(13)、式(14)構建內插虛擬陣列協方差矩陣的參考矩陣；8)通過式(15)～式(17)的優化設計，求重建的內插虛擬陣列協方差矩陣；9)通過式(18)進行譜峰搜索，獲得DOA估計值。

4 仿真實驗

利用MATLAB仿真實驗來檢驗算法性能，實驗采用一對m=3,n=5的互質整數。

實驗1不同信源數算法的仿真性能

假設空間中有7個均勻分布于[-60,60]的信源，信噪比為20 dB，采樣快拍數為T=200，互質陣列和移位互質陣列均可以對7個信源進行有效實現如圖6(a)；當信源增加到10個時，互質陣列空間譜估計存在信源缺失情況，移位互質陣列可以對這10個均勻分布于[-45,45]的信號進行有效估計如圖6(b)；通過本文算法，虛擬域連續陣元范圍是[-13,13]，從而可以對13個均勻分布于[-60,60]的信源有效實現如圖7。說明虛擬陣列內插能夠有效利用虛擬陣列所提供的全部陣列自由度。

圖6 自由度性能對比

圖7 虛擬內插下的自由度性能

實驗2 不同信噪比和快拍數下算法精度性能估計

為了驗證改進算法的估計精度，定義均方誤差數學表達式如下

(19)

式中K為波達方向個數，Q為蒙特—卡羅次數，θk,q為第q次蒙特—卡羅實驗的第k個信號的估計角度，θk為第k個DOA。取Q=200的實驗平均值為最終結果。本文算法對比于簡單互質陣列MUSIC算法和移位互質陣列SS-MUSIC算法如圖8所示。根據仿真結果表明，隨著信噪比的不斷增大和快拍數的不斷增加，本文算法均方根誤差最小，因此本文算法性能優于原互質陣列算法和移位互質陣列空間平滑算法。

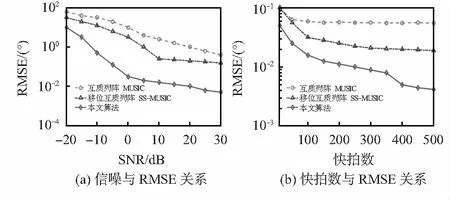
圖8 算法精度估計性能對比

5 結 論

針對互質陣列可估計信源數不足，自由度仍低的問題。本文提出一種移位互質陣列內插虛擬陣列協方差矩陣無網格化重建算法，對互質陣列進行移位處理，明顯增加虛擬陣列陣元數量，提高陣列自由度；采用虛擬陣元內插的方法，將非均勻虛擬陣列轉變為一個均勻虛擬陣列，增大虛擬陣列孔徑；最后，通過對原子范數最小化的優化設計和協方差矩陣稀疏重建來進行DOA估計。仿真結果表明：本文算法將虛擬域信息全部有效用于DOA估計中，極大地獲得自由度的提高，并且無網格化重建算法使估計精度等性能也有較大提高。