基于強化學習的六足機器人動態避障研究*

董星宇， 唐開強， 傅匯喬, 留滄海， 蔣 剛

(1.西南科技大學 制造科學與工程學院，四川 綿陽 621000；2.南京大學 工程管理學院 控制與系統工程系，江蘇 南京 210093；3.制造過程測試技術省部共建教育部重點實驗室，四川 綿陽 621000；4.成都理工大學 核技術與自動化工程學院，四川 成都 610059)

0 引 言

地震救援機器人需要在非結構環境下實現救援搜索任務，六足機器人在復雜環境下行走高效，且具有較好的穩定性，是未來救援機器人的一大選擇[1]。地震救援環境復雜,且震后易發生余震，救援環境由靜態變為動態，機器人需要擁有動態避障能力。傳統的移動機器人動態避障常用人工勢場法、快速擴展隨機樹和動態窗口法等方法[2～4]。但是傳統的動態避障方法，移動機器人需要依賴地圖信息，不能在未知、動態、復雜環境下通過自身的傳感器與環境交互進行避障決策。

近年來,由于深度學習(deep learning,DL)與強化學習(reinforcement learning,RL)得到國內外專家的廣泛研究，涌現出大量基于深度強化學習(deep reinforcement learning,DRL)的機器人避障的研究成果。文獻[5]提出對無人駕駛船舶在未知環境干擾下的深度強化學習避障算法。文獻[6]提出了一種基于深度增強學習的AGV移動機器人，創建了一個移動機器人避障和導航模型。但傳統深度強化學習即深度Q學習網絡(deep Q-learning network，DQN)易出現收斂速度慢，算法偏差變大，難以收斂到最優動作狀態值，而降低機器人動態避障的效果。

在不依靠環境信息的情況下，本文研究將六足機器人上的激光測距儀采集距離數據作為雙重深度強化學習即雙重DQN(double DQN,DDQN)的輸入項，將速度與行進方向作為單片機控制輸出，將每個時刻采集的傳感器數據整合作為馬爾可夫狀態空間。結合傳統DQN與雙重深度強化學習DDQN算法相對比，對六足機器人進行訓練、測試、驗證。

1 雙重深度強化學習算法

1.1 六足機器人運動建模

相對于傳統的輪式和履帶式機器人，六足機器人對復雜地形的適應能力更強但結構設計和步態規劃卻較為復雜。實驗通過運動學逆解得到機器人腿部股、髖和膝三個關節角度，建立笛卡爾坐標系進行足端軌跡規劃，控制舵機聯合轉動使六足機器人移動。

六足機器人的三足步態即通過控制機身一側的前足、后足與另一側的中足在運動時交替處于支撐相和擺動相[7]。圖1為六足機器人在各步態下行進周期的穩定性表現，角度波動范圍越小，機器人行走穩定性越好。圖1(a)為三足步態，圖1(b)為四足步態，圖1(c)為五足步態，由圖分析可知三足步態相較于另外兩種步態雖然穩定性較小但其具有運動效率高，控制簡單等優點。因本次實驗環境不涉及較為復雜的多結構路面，故采用三足步態作為六足機器人的輸出動作步態。

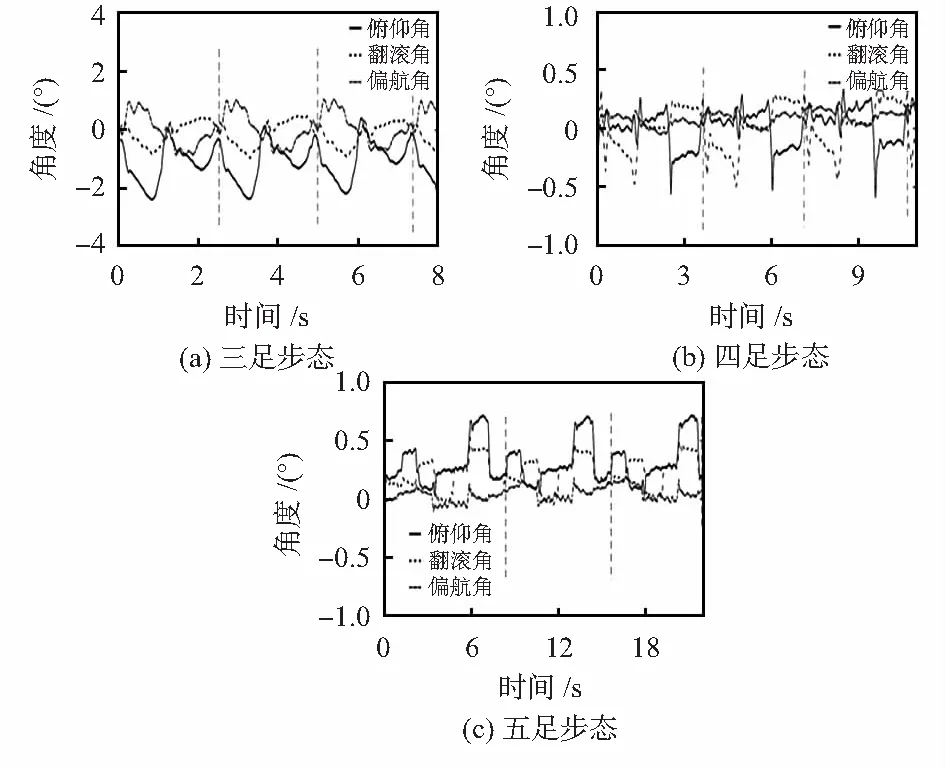
圖1 六足機器人行進步態特征

1.2 強化學習

強化學習為一種標記延遲的監督學習，六足機器人在某t時刻感知的環境狀態為st，通過策略采取動作at達到另一狀態st+1，由環境反饋獲得交互動作的獎懲回報rt，與環境交互的整個過程表現為馬爾科夫決策序列過程，整體可以表示為(st,at,rt,st+1)[8]。

經典的強化學習Q-learning算法通過當前狀態和動作決策進行不斷試錯，其目標是使總折扣回報最大化[9]。然而，傳統的Q-learning算法對輸入變量的復雜性非常敏感。當離散的值函數面對高維或連續的狀態空間時，必然會大大增加計算時間，并導致難以收斂，甚至引發維數災難[10]。

2015年，Silver D提出了一種基于卷積神經網絡(con-volutional neural network,CNN)的深度強化學習算法DQN，它是由多層神經網絡組成的深度強化學習，作為替代傳統離散值函數的一種解決方案。神經網絡強大的適應能力使得逼近動作值函數成為可能。并且通過使用深度強化學習，將狀態變量為矩陣形式的大量輸入替換為一個連續變化的函數值，從而解決了維數災難的問題[11,12]。

1.3 DDQN算法

雖然基于DQN的策略在一些機器人動態避障的問題上得到了成功的應用，但是在選擇行動和評價價值函數時使用相同的網絡存在一定缺陷，這可能導致對結果的過度樂觀估計[13]。為了避免這種情況產生，使用一種雙重深度強化學習算法，其與傳統DQN結構類似，同樣具有兩個相同結構的Q網絡。但與其不同，DDQN通過解耦目標Q值動作的選擇和目標Q值的計算來消除過度估計的問題和使用經驗回放來避免訓練數據的相關性[14]。通過實際動作價值Q網絡在現實中訓練參數，迭代C次后將權重復制更新到目標動作價值Q網絡中以降低過估計對訓練結果的影響。DDQN的目標值可以定義如下

Qtagret=r+γQ(s′,argmaxaQ(s′,a|w)|w′)

(1)

式中γ為折扣因子，w為Q現實中網絡結構權重，w′為Q估計中網絡結構權重,s′為下一時刻感知的環境狀態，a為選擇的動作，r為獎懲回報值。DDQN模型示意如圖2所示。

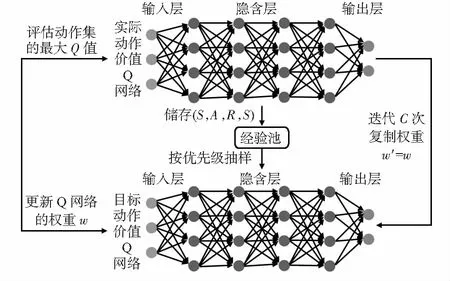
圖2 DDQN模型

2 機器人運動決策模型

2.1 數據預處理

為了提高訓練的收斂速度，保證訓練后的模型具有較好的效果，將機器人與環境交互得到的輸入數據進行降維化處理[15]，通過傳感器距離數據集輸入來避免高維深度信息帶來的收斂速度較慢和計算復雜的問題。將六足機器人不能夠跨越的地方看作障礙物，滿足六足機器人運動學參數要求的路況作為可通過的路徑。

通過激光測距儀和超聲波傳感器采集距離數據集，得到機器人在行進過程中與局部障礙物距離的數據矩陣，機器人行進速度為vrot，采集下一組數據集間隔時間為t，根據公式可判斷出障礙物運動速度vbar

(2)

式中xt為機器人距障礙物在t時刻的距離，sbar為障礙物運動狀態值，設立相對速度的閾值為3 cm/s，當vbar>3時標定障礙物運動狀態為動態障礙物，令sbar=1；反之標定為靜態障礙物，令sbar=0。通過加速度傳感器進行慣性導航，來確定機器人在行進過程中的位置，以此來判斷機器人是否到達目的地。當數據集出現異常值即出現不正常數據時，此時通過運動學的方式控制機器人的運動。數據集正常情況時，將數據集、障礙物運動狀態值和障礙物運動速度作為機器人的狀態，進行雙重深度強化學習訓練網絡參數。

六足機器人的動態避障算法主要運用卷積神經網絡對機器人在局部環境中，如圖3中坐標軸對應的四個方向特征提取障礙物的距離和速度數據。

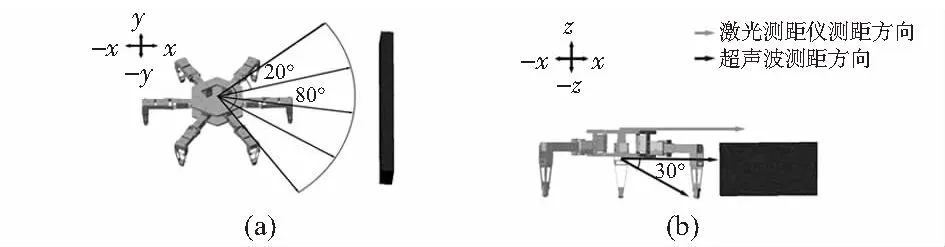
圖3 避障建模效果

在實際情況下障礙物并非質點，為保證六足機器人在行進過程中能感知障礙和具有實際避障能力，四個方向的取值角度為80°，間隔20°取值一次，即一個方向取值個數為5次，如圖3(a)所示。其避免因數據取值過少而導致六足機器人避障失敗。機器人機身全長為lhex，安全距離系數為ε，則機器人有效移動的安全距離為

dsafe=ε·lhex/sin40°

(3)

故當d0°≥dsafe或d80°>dsafe時,機器人可進行避障后的有效動作，否則視為機器人還未成功躲避障礙。

六足機器人攀爬臺階的能力是通過機身底部兩個不同放置方式的超聲波傳感器判定，如圖3(b)所示。當傾斜30°放置的超聲波和同方向激光測距儀檢測的距離無較大改變，而水平放置的超聲波檢測到障礙物則執行向上攀爬動作；當水平放置的超聲波和激光測距儀檢測距離無較大改變，傾斜30°放置的超聲波檢測距離突變，則執行向下攀爬動作。臺階高度位置應處于機器人底盤高度和激光測距儀放置高度之間。

2.2 DDQN模型

強化學習模型所建立的神經網絡設計為一層輸入層，四層隱藏層和一層輸出層，網絡輸出為各個動作對應的Q值，選擇對應最大Q值的動作和環境相交互。樣本池采用優先級抽樣，樣本的時序差分誤差越TDerr大，其訓練價值越高，被選中概率增加。DDQN策略的逼近器采用卷積神經網絡，其模型的優化目標函數L(ω)為

TDerr=Qtagret-Q(s,a|ω)

(4)

L(ω)=E[(TDerr)2]

(5)

本文通過運用增量式ε-greedy探索和利用策略。在成功到達一定終點次數前，為保證探索率足夠，設置εmax∈(0,1)，成功到達目標次數N(suc)和增量Δε，由式(6)每回合更新ε值

ε=ε+ln(N(suc)+2)·Δεandε≤εmax

(6)

由取值[0,1]的隨機數rand()與ε值比較，在當前時刻選擇最優動作和探索未知狀態進行平衡，加快神經網絡模型收斂的速度，該策略定義為

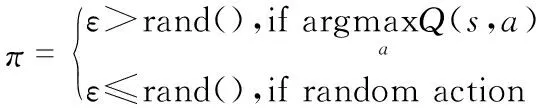
(7)

2.3 動態避障行為與獎懲函數

由于DDQN與DQN方法都具有高維輸入低維輸出的特點，故六足機器人的執行動作設計為11個離散性動作的輸出。如表1所示。

表1 執行動作設計

六足機器人通過控制舵機轉速和軌跡斷點數協同調節行進速度，舵機運行誤差積累增加而導致偏航角發生改變。偏航角越大機器人行走偏移量越大，圖4表示出機器人在三足步態下行走路程為120 cm時，3種代表性的不同行進速度下偏航角隨時間的變化。

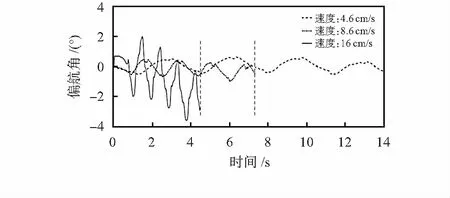
圖4 不同行進速度下偏航角對比

由圖4可知，為保證在速度和偏航角之間相對平衡，六足機器人在執行攀爬動作時為尋求機身穩定，采用行進速度為4.6 cm/s；而速度為8.6 cm/s比速度為4.6 cm/s時的偏航角誤差改變量較小，速度卻提高了進一倍，因此在無障礙和靜態障礙物時，六足機器人以8.6 cm/s的速度行走；而當六足機器人在應對動態障礙物時，為保證躲避速度的要求，使機器人在滿足能夠承受最大偏航角誤差下以速度為16 cm/s行走。

通過目標任務主次級分層制定獎勵函數避免獎勵稀疏，主任務為到達目標位置給予較大獎勵；次級任務為靜態、動態避障和快速抵達目標位置。定義機器人對障礙物最短距離為disrot。當disrot<0.2 m時，視為一次碰撞，給予懲罰值。根據機器人與目標位置的相對距離disFin進行獎勵塑形，取0.4做為懲罰因子，相對距離越小懲罰值越小同時機器人停止不動給予懲罰。應對動態障礙時，防止因動態障礙物未完全駛離而導致機器人復碰撞情況產生，如圖5所示。

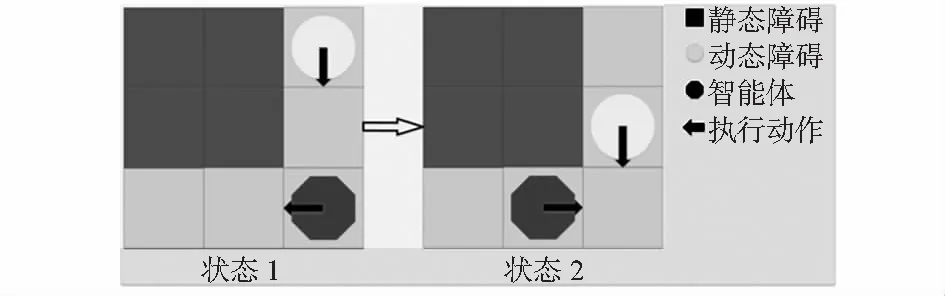
圖5 復碰撞情況示意

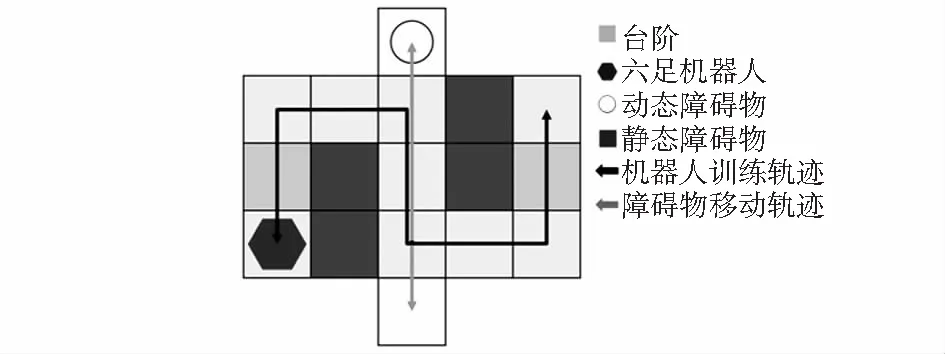
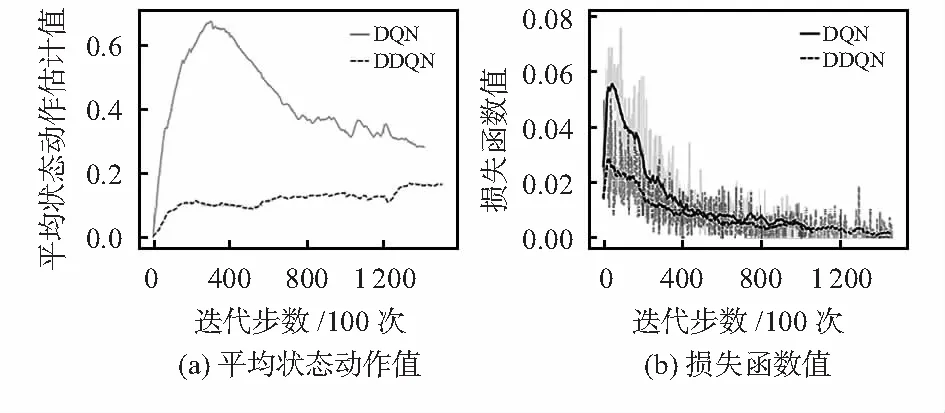
根據vbar和vrot估算出預計相撞時間為t0和預計躲避時間為t1。當t0>t1時，機器人躲避方向選擇與障礙物移動方向一致時給予獎勵；當t0

R=-(disFin)0.4+Rm(disrot,disFin|t0,t1)

(8)

3 實驗結果與分析

3.1 實驗平臺描述

機器人移動平臺為18個自由度的六足機器人，驅動硬件為單片機STM32F4。為解決運算速度的問題，電腦通過TensorFlow計算更新神經網絡權重，根據策略決定執行的動作數據，通過ATK—HC05藍牙模塊與串口進行全雙工通信，傳輸數據至單片機。機器人執行動作后將觀測值反饋給電腦進行下一次更新，通過上下位機數據傳輸的方式避免單片機內存不足導致的計算速度緩慢，時延過大的問題。

3.2 實驗過程設計

通過在實驗室搭建實驗環境，為提高強化學習訓練效率，本文采用對稱式搭建尺寸大小為5.6 m×3 m的迷宮場景，機器人完成一次抵達終點任務后，目的地與起始位置交換；實驗動態障礙物為四驅小車，小車沿移動軌跡以10 cm/s均速行進，每次行進到軌跡末端會等待3 s后再反向移動以此避免機器人很難避過小車抵達終點而導致損失函數難以收斂的情況；六足機器人訓練軌跡和動態障礙物移動軌跡如圖6所示，實際搭建的實驗場景如圖7所示。

圖6 訓練示意

圖7 算法驗證實驗環境

本次實驗設置兩組相同網絡模型參數的DQN和DDQN算法，網絡模型訓練參數：經驗回放池樣本數為12 000個，回合訓練批量為60個，折扣回報系數為0.9，網絡梯度動量為0.9，學習率為0.01，網絡權重更新回合為100。令通信中的六足機器人在搭建好的迷宮內進行循環訓練。在規定回合后機器人停止行動，對比兩種算法的訓練效果。

3.3 實驗結果與分析

六足機器人的動態避障實驗結果局部截圖如圖8所示，圖8中(a)～(f)六種情況在全局環境下發生位置與圖7中的標號相對應。

圖8 六足機器人動態避障實驗

在應對靜態障礙物時，機器人通過策略選擇常速動作穩定避開靜態障礙物，如圖8(a)所示；強化學習策略根據次級任務獎懲函數的設定，使機器人以最短回合數抵達終點，如圖8(b)所示；應對動態障礙物時，機器人向旁側閃避時間低于與小車相撞時間且旁側無障礙物，則學習策略傾向于采取向旁側躲避,等待小車完全駛離后再向前行進，以避免復碰撞的產生，如圖8(c)所示；當機器人向旁側閃避時間高于與小車相撞時間，學習策略大概率采取與小車運動方向同向移動, 如圖8(d)所示；神經網絡通過訓練傳感器采集得到的距離數據集，機器人成功對臺階進行攀爬，如圖8所示。

圖9為DQN與DDQN兩種不同算法訓練機器人動態避障后的結果對比。圖9(a)可知，DDQN有效減少了平均狀態動作值的過度樂觀估計。圖9(b)可以看出DDQN比DQN的損失函數收斂速度快。

圖9 DQN與DDQN算法避障結果對比

4 結 論

針對移動機器人在智能決策控制下的動態避障問題，本文提出基于雙重深度強化學習的六足機器人動態避障算法，與傳統的深度強化學習方法進行比較，證明了雙重深度強化學習在迭代訓練收斂速度和防止算法結果偏差變大表現出更好的性能，六足機器人能夠有效完成簡單的動態避障任務。但本次實驗的環境建模較小，只是針對性進行建模，故還不能應用于復雜的環境中，仍需要進一步研究。