電力系統交直流潮流的全純嵌入計算

姜 濤 張 勇 李 雪 李國慶 陳厚合

電力系統交直流潮流的全純嵌入計算

姜 濤 張 勇 李 雪 李國慶 陳厚合

（現代電力系統仿真控制與綠色電能新技術教育部重點實驗室（東北電力大學） 吉林 132012）

針對采用牛拉（NR）法計算電力系統交直流系統潮流存在初值選取和計算量大的不足，提出一種用于交直流潮流計算的全純嵌入方法。該方法首先依據全純函數構造原理，通過嵌入參數，分別構建全純交流潮流模型、直流潮流模型及換流站控制模型；然后，基于全純函數的泰勒級數展開特性，將非線性全純潮流方程的求解問題，轉換為隱式全純函數的顯式化問題；依據同次冪系數相等原則，求取泰勒級數展開項的冪級數系數，完成全純函數的顯式化，進而對嵌入參數賦值，實現交直流潮流的快速求解；最后，通過修改的IEEE 5節點交直流系統、RTS-96交直流系統和波蘭電網3012wp交直流測試系統進行分析和驗證，結果表明，所提方法不依賴初值便可快速、準確地計算出交直流系統潮流，且魯棒性強，為大規模交直流電網潮流計算提供了新思路。

交直流系統 電壓源型換流器 全純函數 潮流計算

0 引言

基于電壓源型換流器（Voltage Source Converter, VSC）的柔性直流輸電技術具有傳輸容量大、可控性強等諸多優點，已成為解決用電需求增長、大規模新能源并網等問題的有效手段[1-4]。近年來，我國柔性直流輸電工程數量和規模不斷增加，大規模交直流混合輸電已成為我國電網典型形態[5-6]。然而，大規模交直流混合輸電系統拓撲結構的復雜性和直流系統控制模式的多樣性，給快速、準確獲取交直流電網潮流分布帶來極大挑戰[7-8]，研究適用于計算大規模交直流系統潮流的新方法，對交直流電網規劃運行、穩定分析、可靠性評估等具有重要意義。

當前，交直流電網潮流計算方法主要分為統一求解法和交替求解法[9]：統一求解法將交流潮流方程和直流潮流方程進行聯立求解[10]；交替求解法則對交流電網潮流和直流電網潮流交替求解，并利用換流站實現交直流潮流信息交互[11]。文獻[10,12]將交流潮流修正方程和直流潮流修正方程進行聯立，并基于牛拉（Newton Raphson, NR）法求解該修正方程，實現交直流潮流的統一求解。然而該方法在實際應用中存在以下瓶頸：①當交直流電網規模增大時，Jacobi矩陣維數劇增，修正方程求解速度降低；②換流站控制方式切換將使迭代計算次數增加。因此，統一求解法難以滿足大規模交直流電網潮流計算效率的需要[11]。交替求解法可擴展性強、靈活性高，且有效降低了潮流方程的維數，在實際工程中得到了廣泛應用[13-14]。文獻[14-15]建立了VSC換流站的穩態潮流模型，并基于NR法分別計算交流電網潮流與直流電網潮流，實現交直流系統潮流的交替求解。然而，基于NR的交替求解法在交直流潮流信息交互的大循環和節點電壓修正的小循環中均會引起節點功率變化，需修正Jacobi矩陣對應元素，并重新對Jacobi矩陣求逆，計算量較大，且節點功率變化較大時易造成Jacobi矩陣奇異[16]；其次，NR法對初值比較敏感，不合理的初值有可能導致交直流潮流計算耗時增加，甚至無法收斂[17]。

為解決NR法在潮流計算中的不足，西班牙學者A. Trias博士于2012年提出利用全純函數嵌入法（Holomorphic Function Embedding Method, HEM）求解電力系統潮流的新思路，該方法具有良好的收斂性，且無需提供初值[18]。文獻[19-20]進一步提出了PV節點的全純潮流模型，完善了交流系統潮流計算的全純嵌入算法。然而，現有HEM相關研究多應用于交流系統，對交直流混合系統的潮流計算鮮有研究。此外，多端互聯交直流混合輸電系統的潮流計算需同時考慮交流電網潮流、直流網絡潮流及換流站控制方式，僅由交流全純潮流計算方法簡單地推廣至直流潮流計算中，難以適用于控制方式靈活多變的多端交直流輸電系統。因此，開發適用于交直流系統的全純嵌入潮流求解算法亟待研究。

針對上述問題，本文提出了電力系統交直流潮流的全純嵌入計算方法。首先，針對傳統潮流計算中的節點功率平衡方程，通過嵌入參數構建全純交流潮流模型和全純直流潮流模型，同時計及換流站的控制特點，構建換流站的全純控制模型；然后，基于全純函數的泰勒級數展開特性，將非線性潮流方程的求解問題轉換為隱式全純函數的顯式化問題；進而，依據同次冪系數相等原則，求取泰勒級數展開項的冪級數系數，以實現隱式全純函數的顯式化，并對嵌入參數賦值求取系統潮流解；最后，通過修改的IEEE 5節點交直流系統、RTS-96交直流系統和波蘭電網3012wp交直流測試系統對所提方法進行分析和驗證。

1 交直流系統基本描述

含VSC換流站的交直流系統結構示意圖如圖1所示。圖1中sp和sp分別表示第個VSC換流站注入交流系統公共耦合點（Point of Common Coupling, PCC）的有功和無功功率，dc和dc分別表示直流節點有功功率和節點電壓。

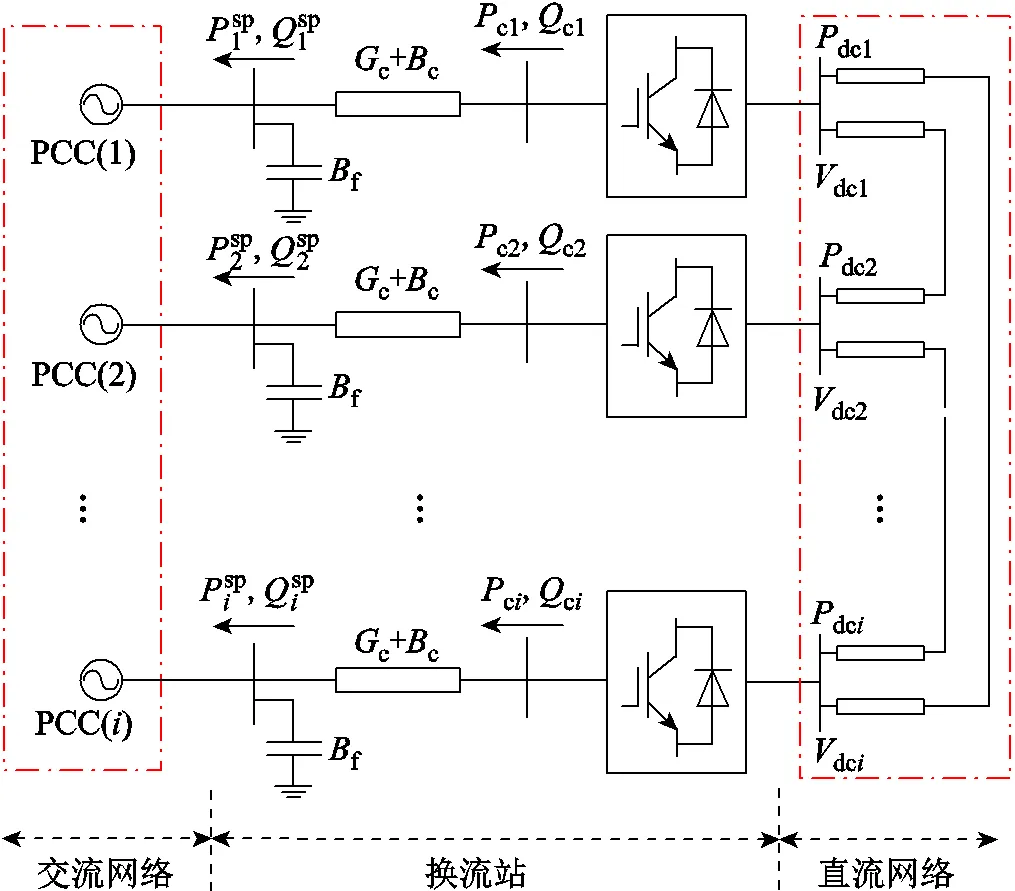
圖1 交直流系統結構示意圖

圖1中，交直流系統潮流模型可分為交流潮流模型、直流潮流模型和VSC換流站信息交互模型。極坐標系下交流側潮流模型可描述為

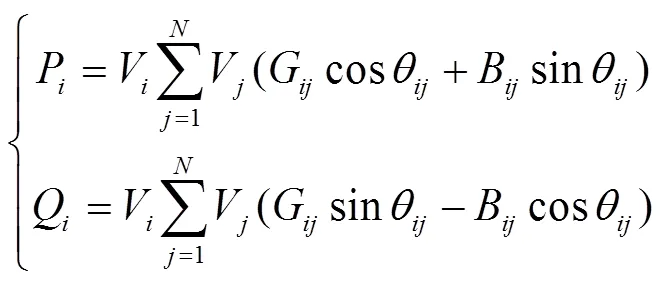
式中，V、V分別為節點和的電壓幅值；為節點與的電壓相位差；P與Q分別為節點的有功和無功注入量；G與B分別為節點與之間的電導與電納；為交流電網節點數。

直流潮流模型可表述為

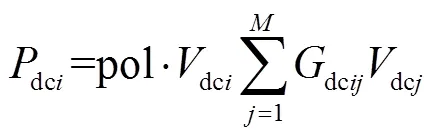
式中，dc為直流節點的有功功率；dc為直流節點的電壓；dc為直流節點與直流節點之間的電導；為直流系統節點數；pol為直流電網輸電極數。

換流站信息交互模型主要包括換流站交流側的有功平衡方程、無功平衡方程及換流器有功功率平衡方程[9]，具體形式為

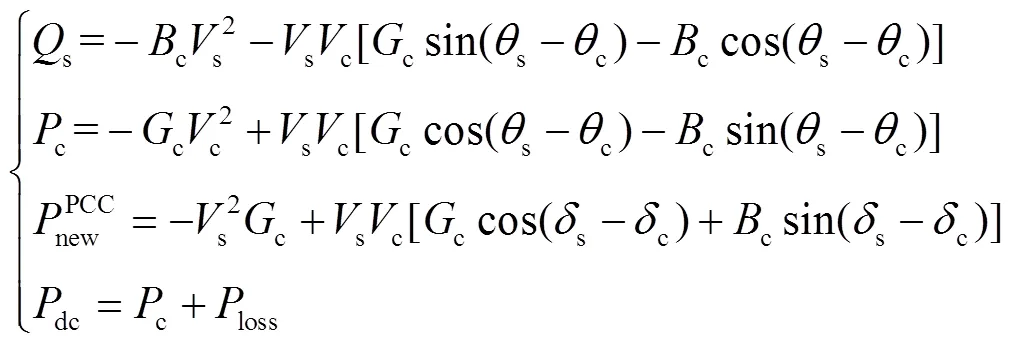
式中，c為流過換流器的有功功率；dc為直流側有功功率；loss為換流站損耗；s為換流器注入PCC節點的無功功率；PCC new為換流站注入PCC節點的更新值；c為換流站等效電納；c為換流站等效電導；s為PCC節點電壓幅值；c為換流器母線電壓幅值；s為PCC節點電壓相角；c為換流器母線電壓相角。

對式（1）～式（3）所構成的交直流系統潮流方程，目前常用的求解方法是NR法。雖然NR法已在交直流系統的潮流計算中發揮出重要作用，但在實際應用時仍存在計算量較大、對初值敏感、Jacobi矩陣易奇異等不足。為此，本文提出一種基于HEM的交直流潮流全純嵌入計算方法。

2 交直流潮流的全純潮流模型構建

為解決傳統NR法在交直流潮流計算中的不足[10-15]，本節首先基于全純函數嵌入原理，在直角坐標系下，分別構建含全純函數的交流潮流計算模型、直流潮流計算模型及換流站控制模型，進而實現交直流系統的全純潮流模型構建。

2.1 全純函數嵌入原理

2.1.1 全純函數構造原理初始振幅系數建立

若函數()定義域內每一點的鄰域均無限可微，則稱()為全純函數[21]，其在定義域內0處展開的泰勒級數可表示為

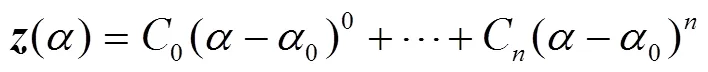
式中，C為泰勒級數展開第項冪級數的常系數。

對非線性方程，有

若待求量難以直接求解時，全純函數嵌入法通過嵌入新的復變量，構造隱式函數()，并嵌入到原方程中形成含有全純函數的方程，即

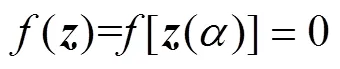
通過對函數()進行泰勒級數展開，求解其冪級數系數并代入式（4），可將該隱式函數()轉換為有具體表達式的顯式函數，進而對變量賦值得到()的具體值，即為()的解。

2.1.2 全純函數構造條件

為保證全純函數嵌入法的正確應用，構造全純方程時應滿足以下條件[22]：①所構造的隱式函數()在定義域內連續且解析，即該函數具有全純性；②由斯塔爾定理可知，在到達鞍節分岔點前的路徑上，[()]=0具有唯一解，不存在多個解合并的異常點，異常點僅在鞍節分岔點處存在；③當=0時，方程[(0)]=0的解[0]（即“冪級數常數項”）真實存在，且相對容易求取；④當=1時，[(1)]等價于()，從而保證=1時，(1)的值即()=0的數值解。

2.2 交流全純潮流模型

由2.1節可知，通過對式（5）所示的非線性方程嵌入復參數構造全純函數，可將非線性方程求解問題轉換為隱式全純函數的顯式化問題，進而實現非線性方程的求解。本節將該求解思想應用于交流側潮流求解中，分別構造如下交流系統PQ、PV及平衡節點的全純潮流方程。

1）PQ節點全純潮流方程。通常PQ節點注入功率已知，待求量為節點電壓幅值和相角，其復數形式的節點功率平衡方程為

式中，Y,tr為節點與節點之間的線路導納；Y,sh為節點對地自導納；S為節點注入功率；V為節點電壓；“*”表示共軛運算。

顯然，式（7）是關于節點電壓V的多元非線性方程，根據2.1節所述全純函數構造原則，在原方程中嵌入復參數（=+j，其中,∈R），構造關于節點電壓V的全純函數V()，故PQ節點全純潮流方程為

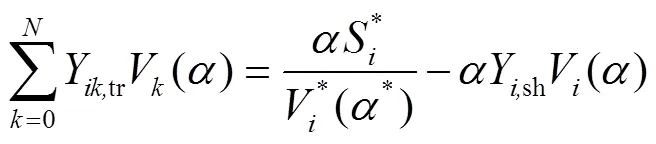
由全純函數充要條件，函數()滿足柯西-黎曼方程，()為全純函數，且文獻[18]已證明全純潮流模型滿足條件②，因此所構造PQ節點全純潮流方程滿足2.1.2小節所述構造條件①與②。

由于函數()是全純函數，將其在(0，j0)處泰數展開，并進一步化簡為冪級數形式，即

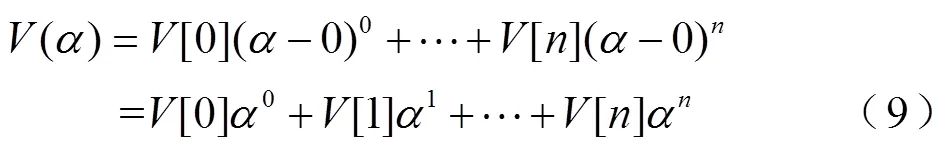
又由式（8）可知，當=0時，非線性潮流方程式（8）轉換為關于V[0]的線性方程組，便可求取V[0]數值；當=1時，式（8）與式（7）等價，故(1)的數值即為節點電壓值。因此式（8）滿足2.1.2小節所述構造條件③與④。

2）PV節點全純潮流方程。PV節點通常已知節點電壓幅值和節點注入有功功率，待求量為節點電壓相角和注入無功功率。同理，構造PV節點的全純潮流方程為

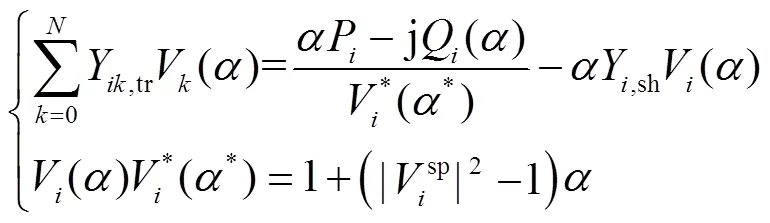
3）平衡節點全純潮流方程。平衡節點通常已知節點電壓的幅值和相角，待求量為節點注入的有功和無功功率。為便于全純潮流模型的求解，構造平衡節點全純潮流方程為

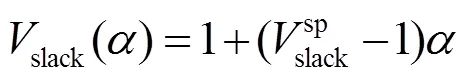
式中，sp slack為平衡節點設定的電壓；slack()為交流平衡節點的電壓全純函數。

2.3 直流全純潮流模型

不同于交流電網，直流電網的功率和電壓均為實數值，但實數域包含于復數域內，故全純嵌入法在直流電網潮流計算中依然適用。直流網絡節點類型主要分為定直流功率節點和定直流電壓節點，針對這兩類直流網絡節點類型，本節分別構造如下直流全純潮流方程。

1）定直流功率節點全純潮流方程。此類節點通常已知節點有功功率dci，待求量為節點電壓dci。依據全純函數的構造條件，通過嵌入實數域參數構造節點電壓dci的全純函數，進而得到定直流功率節點的全純潮流方程為

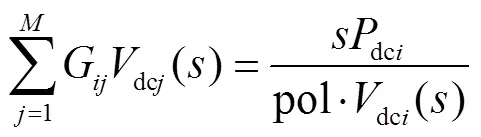
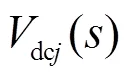
2）定直流電壓節點全純潮流方程。此類節點通常已知節點電壓dci，節點有功功率dci待求，為便于全純潮流模型的求解，構造該節點的全純直流潮流方程為

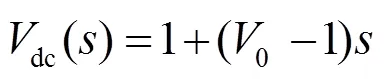
2.4 VSC換流站控制模型

換流站是連接交流系統與直流網絡的關鍵環節，在交直流系統潮流計算中，換流站潮流計算模型包括換流站等值模型、損耗模型及控制模型[23-25]。由于換流站等值模型和損耗模型的相關研究較為成熟[15]，因此，本文重點關注換流站全純控制模型的構建，有關換流站等值模型和損耗模型可詳見文獻[14]。VSC換流站控制方式可分為有功類控制和無功類控制兩大類，且不同控制方式間還存在轉換。針對換流站的控制方式及控制方式轉換特點，本節分別構建VSC換流站的有功類和無功類全純控制模型。

2.4.1 有功類控制全純潮流方程

有功類控制也稱為直流側控制，可直接控制直流電網的傳輸功率及節點電壓，通常可分為定直流功率控制與定直流電壓控制，其對應的全純潮流模型構建如下：

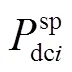
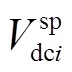
2.4.2 無功類控制全純潮流方程

無功類控制也稱為交流側控制，可間接影響交流電網傳輸的無功功率及電壓幅值，通常分為定無功功率控制與定交流電壓控制，其對應的全純潮流模型可構建為：

（1）定無功功率控制全純潮流模型。定無功功率控制方式下，VSC換流站注入交流側PCC節點無功功率為定值sp，構建定無功功率控制全純潮流模型為

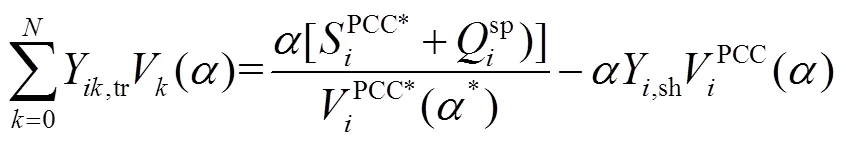
式中，PCC*為交流第個PCC節點的功率的共軛。

（2）定交流節點電壓控制全純潮流模型。定交流節點電壓控制方式下，VSC換流站控制交流側PCC節點電壓幅值為定值sp，構建的定交流節點電壓控制全純潮流模型為

系統正常運行時，需根據交直流系統實際運行情況，對VSC換流站有功類和無功類控制方式進行合理的組合，常用的VSC換流站控制組合方式主要有以下四種：①直流側定spdc控制，交流側定sp控制；②直流側定spdc控制，交流側定sp控制；③直流側定spdc控制，交流側定sp控制；④直流側定spdc控制，交流側定sp控制。

2.4.3 VSC換流站控制方式轉換

正常運行時，為保證換流站安全運行，換流站需適時調整其控制方式，以便換流站運行在安全區域內。圖2為考慮VSC換流站電壓約束和換流站傳輸容量約束的換流站安全運行區域。圖中上、下圓弧為換流母線電壓運行在上、下限時對應的無功功率邊界，圓形區域為換流器傳輸容量約束，左側為整流運行區域，右側為逆變運行區域，陰影部分為VSC換流站實際運行區域。

如圖2所示，若換流站無功類控制方式設置為定無功功率控制，正常運行時處于圖中點，假如交流PCC節點或與之相鄰的節點負荷增加，由于無功不足將導致PCC電壓幅值降低，進而導致換流母線電壓低于其下限值c,min，如圖中點所示。此時需將定無功功率控制轉變為定交流電壓控制，為系統提供無功支撐能力以提高交流節點電壓，系統運行點將移至圖中點，使VSC換流站電壓維持在合理范圍內。若換流站無功控制方式設置為定交流電壓控制，正常運行時處于圖2中點。若PCC節點負荷持續大幅增加，VSC換流站注入交流系統PCC的無功功率s也隨之增加，導致換流母線電壓高于其上限值c,max，如圖中點所示。此時應將VSC換流站控制方式由定交流電壓控制轉換為定無功功率控制，無功功率設定值為換流器傳輸容量約束下的最大無功功率注入值，系統運行在圖中點，避免了換流器潮流越限。

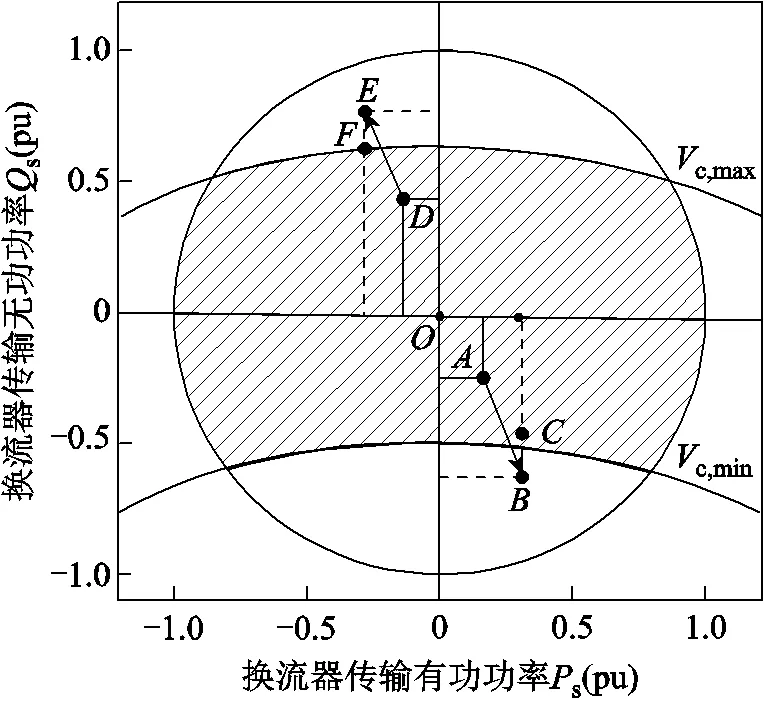
圖2 電壓約束和傳輸功率約束下換流器的運行范圍

3 全純潮流模型求解

針對第2節構建的交直流系統全純潮流計算模型，本節基于交替求解算法分別對其進行求解，以實現交直流系統潮流的求解。

3.1 交流全純潮流模型求解

全純潮流模型求解的關鍵是建立全純函數冪級數系數[]與[-1]之間的遞歸關系，進而求取全純函數表達式并對嵌入變量賦值，即可完成交流潮流的求解。

1）PQ節點求解

為消除式（8）中的分式，進而作如下假設

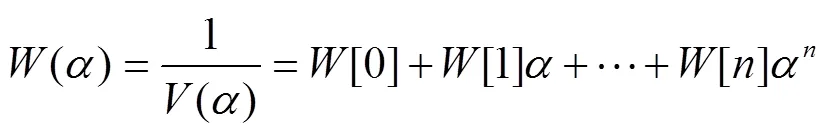
將全純函數在(0，j0)處展開為泰勒級數，并代入式（8）得

式中，V[]為節點電壓冪級數α的系數；為冪級數階次。獲取遞歸關系式（20）后，便可利用低階的[-1]和[-1]求取高階的[]。

又因()和()互為倒數，故滿足

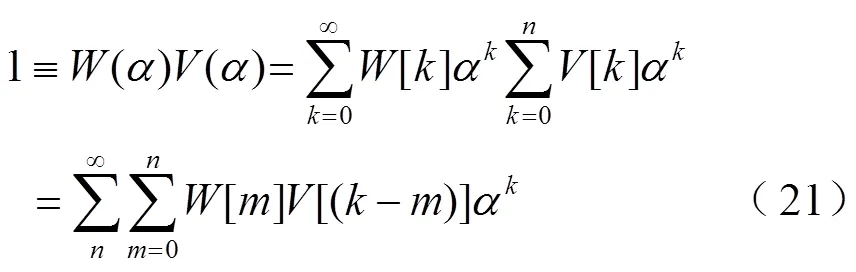
通過比較式（21）等號兩邊同次冪系數可得

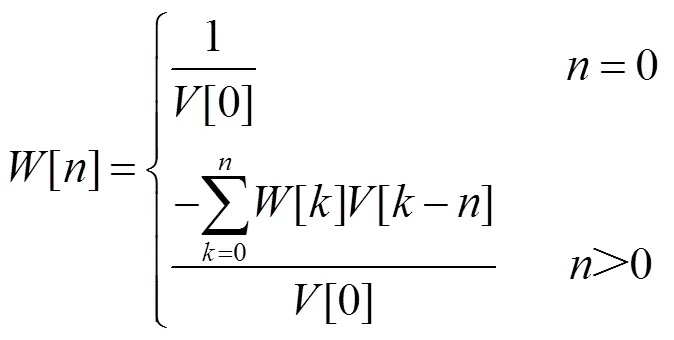
綜上所述，電壓函數的冪級數系數[]求解過程如圖3所示。

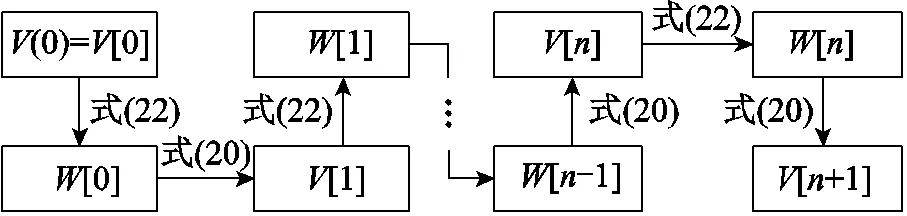
圖3 冪級數系數遞歸求解示意圖

2）PV節點求解

對PV節點，將全純函數進行泰勒展開并代入式（10）中，對比等式兩邊同次α冪級數系數，求得的冪級數系數遞歸式為

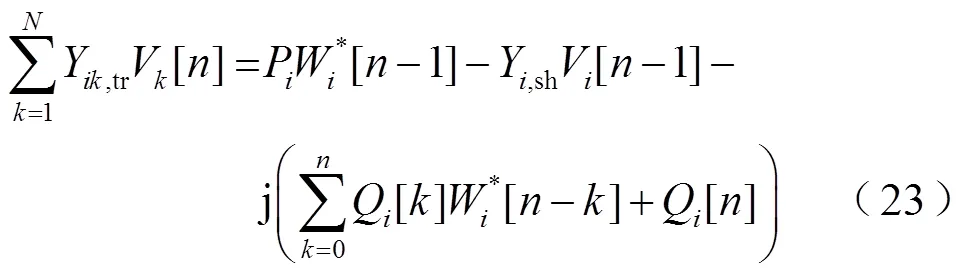
定義新符號Rhs_Known[-1]為

因此，式（23）可進一步表示為

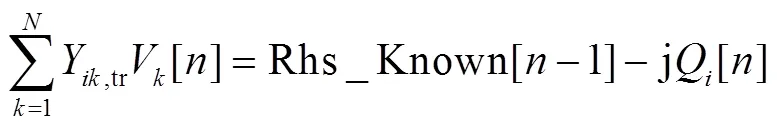
將式（24）中未知量Q[]移至等式左邊，則該等式左邊為第項的系數，等式右邊為第-1項的系數，通過求解該線性方程即可求得PV節點電壓冪級數α的系數。

3）平衡節點求解

根據平衡節點全純模型，對比式（11）等式兩邊同次冪系數，得遞歸式為

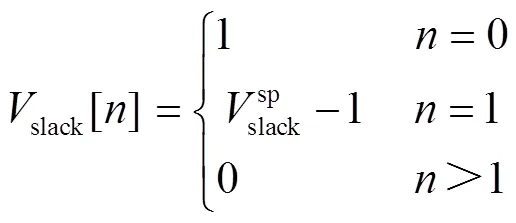
式中，slack[]為全純電壓函冪級數α對應系數。

綜上所述，本文所提基于HEM的交流側全純潮流求解步驟如下：

1）根據2.1節所述全純構造規則，對節點潮流方程嵌入變量，構造式（8）、式（10）和式（11）所示的交流全純潮流模型。

4）利用所求得節點電壓值，計算系統的最大功率不平衡量Δac（ΔacRe(ac(acac)*)）。若Δac大于設定閾值，則繼續計算更高階冪級數系數；若差值小于設定閾值，結束算法，完成交流側潮流求解。

3.2 直流全純潮流模型求解

直流全純潮流模型求解需分別構建定直流電壓節點和定直流功率節點的冪級數系數遞歸關系，求取電壓全純函數的表達式，直流全純潮流求解過程如下。

1）定直流功率節點

為消除式（12）中的分式，定義電壓函數dci()的倒數dci()為

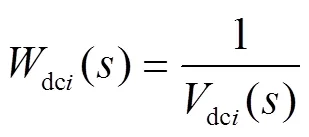
將函數dci()和dci()進行泰勒級數展開為

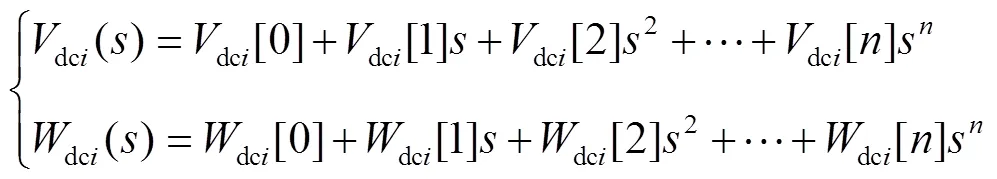
進而將式（28）代入式（27）得

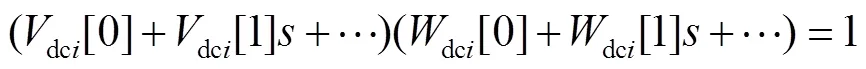
對比等式兩邊同次冪級數系數可得冪級數系數和之間遞歸關系為

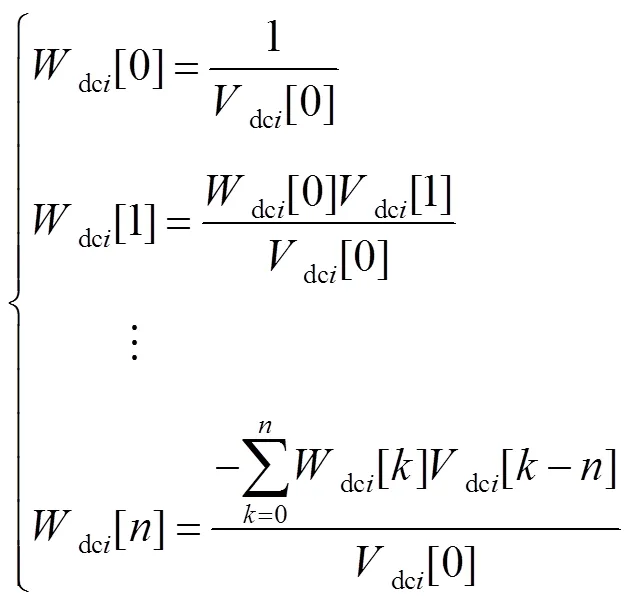
將式（28）代入式（12）并進行冪級數展開為

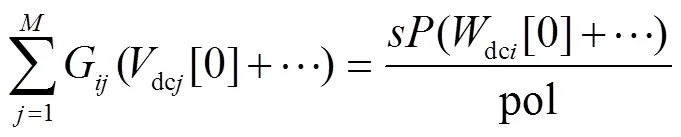
當=0時，代入式（31）可得

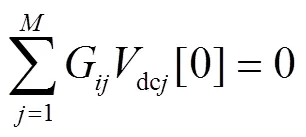
P直接與嵌入變量相乘，在=0時，分子項全部為0，此時非線性潮流方程轉換為線性方程，通過求解該線性方程組可獲得冪級數常數項。

當＞0時，比較等式（31）兩邊同次冪級數系數可得

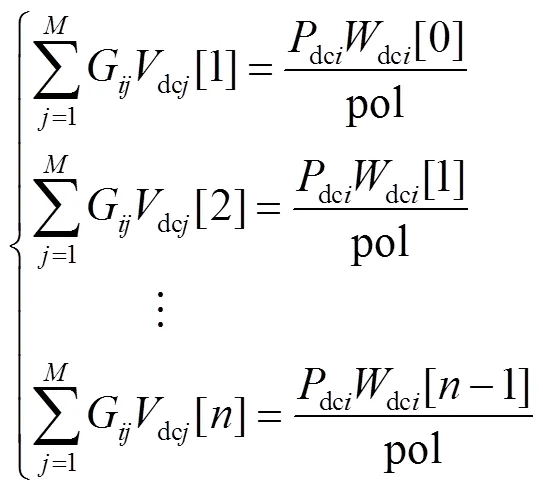
由式（33）得冪級數之間的遞歸關系式，進而可求取任意階數的冪級數系數，實現全純函數的顯式化。

2）定直流電壓節點

將定直流電壓節點的dc()展開為冪級數形式代入式（13）得

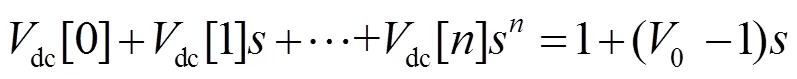
對比式（34）兩邊同次冪級數系數得定直流電壓節點的冪級數系數遞歸關系式為

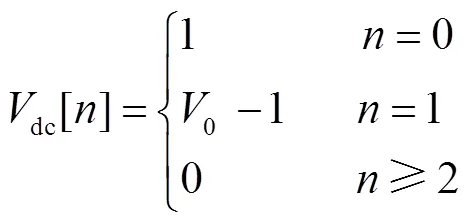
3）構建求解全純潮流模型的線性方程組

在實際潮流計算中，需基于直流電壓冪級數系數的遞歸關系式構建線性方程組，以求解各直流節點電壓的冪級數系數。此處以三節點直流網絡為例，假設節點1和節點3為定直流功率節點，設定有功功率分別為dc1和dc1，節點2為定直流電壓節點，構建線性方程組如式（36）所示。

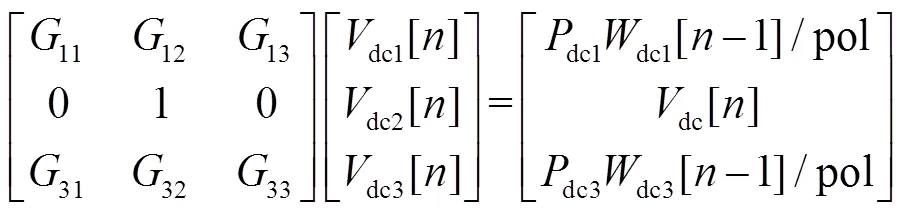
分析式（36）可知，該線性方程組的系數矩陣是節點導納矩陣的一種變形，故該矩陣為常數矩陣且具有較高的稀疏度。同理可知，交流側全純潮流求解中，用于冪級數求解的線性方程組對應系數矩陣，也可由節點導納矩陣變形得到，與傳統NR迭代計算方法相比，潮流計算過程中僅需對該矩陣進行一次求逆運算，有效降低了低潮流計算量。

3.3 交直流潮流信息交互

圖4進一步對比了本文所提基于HEM的交直流潮流求解算法和基于NR法的交直流系統潮流求解算法的異同。顯然，由圖4可知，采用交替求解法求解交直流系統潮流時，本文所提求解算法與NR法在交直流潮流中交互的信息均相同，但在交流側和直流側潮流計算部分，兩者具有顯著的區別：①與NR法相比，本文所提基于HEM的交直流潮流求解算法在求解交流側和直流側潮流時，用于冪級數求解的線性方程組對應系數矩陣為常數陣，在整個交直流潮流交替求解過程中僅需對其進行一次求逆即可，且計算大規模交直流系統潮流時，可提前生成逆陣并存儲，便于在每次遞歸計算中使用，大大縮短了運行時間；而NR法在整個交替求解過程中需進行頻繁的Jacobi矩陣求逆運算，計算量較大。②本文所提基于HEM的交直流潮流求解算法將傳統非線性代數方程的求解問題轉換為隱式函數顯式化的問題，無需為其提供初值便可準確計算出系統潮流解，而NR法對初值比較敏感，不合理的初值有可能導致潮流計算結果不收斂。③本文所提求解算法中，用于冪級數求解的線性方程組對應系數矩陣為常數陣，且矩陣元素僅與線路導納有關，不會出現類似NR法在求解潮流過程中Jacobi矩陣奇異的問題，故所提算法具有較強的魯棒性。

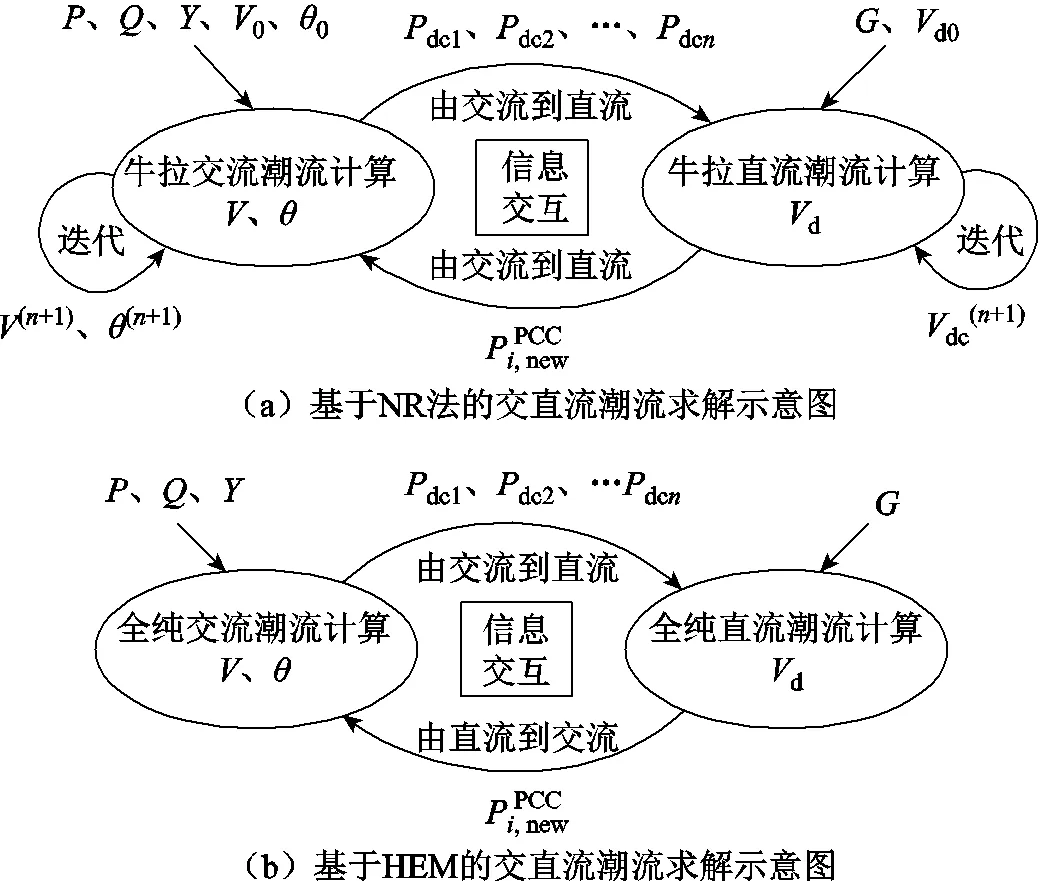
圖4 交直流潮流計算方法對比

3.4 計算流程

綜上所述，本文所提基于HEM的電力系統交直流潮流求解算法流程如圖5所示。具體步驟如下：

1）基于HEM分別構建式（8）、式（10）和式（11）所示的交流全純潮流模型，基于換流站控制方式，構建式（16）或式（17）PCC節點全純潮流模型，并依據式（20）、式（25）和式（26）構建線性方程組，求取交流側潮流分布。

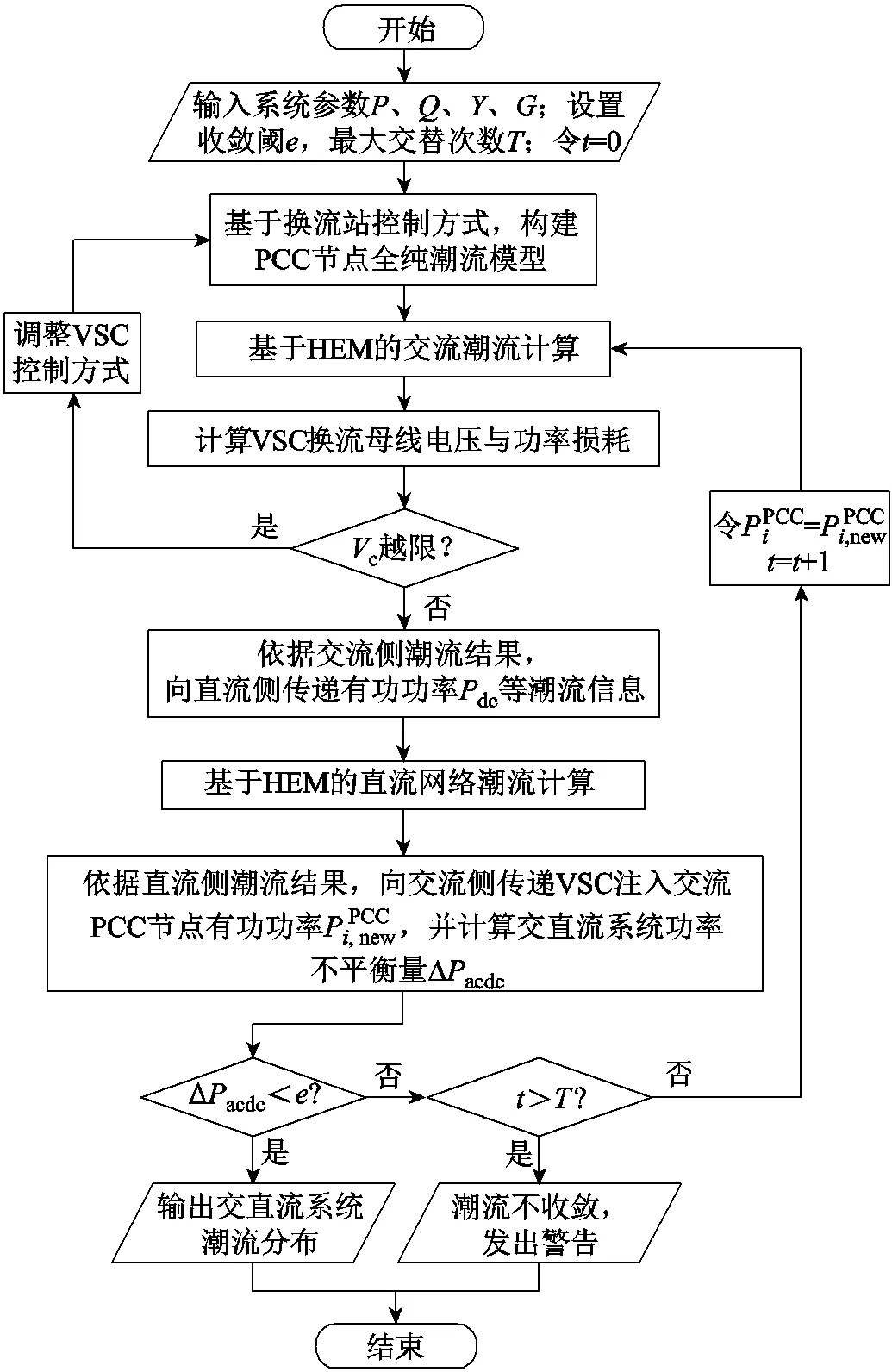
圖5 電力系統交直流潮流的全純嵌入算法流程

2）確定交流側潮流分布后，可將PCC節點電壓PCC與節點功率PCC、PCC視為定值，依據圖1所示換流站等效電路模型，計算換流母線電壓c、換流站損耗loss等相關換流站數據，進而由式（3）求得各直流節點有功功率dc，將交流潮流信息傳遞至直流側。

3）基于HEM構建式（12）和式（13）所示直流全純潮流模型，并依據式（27）～式（35）進行求取直流電壓函數dc()的冪級數系數遞歸公式，進而構建式（36）線性方程組，求取直流側潮流分布。

4）獲取直流潮流分布后，由式（3）計算“定直流電壓”控制的VSC注入交流PCC節點有功功率PCCnew，將直流潮流信息傳遞至交流側；并計算交直流系統之間的功率不平衡量ΔacdcPCC-PCCnew，若Δ大于設定閾值，則繼續執行步驟1）；若Δ小于設定閾值，結束算法，輸出系統潮流結果。

4 算例分析

本節分別通過修改的IEEE 5、RTS-96和波蘭電網3012wp的交直流測試系統對所提基于HEM的交直流潮流求解算法進行分析、驗證，并將結果與文獻[15]開發的基于NR法的交直流潮流開源計算軟件MATACDC進行分析、對比，以驗證所提方法的準確性、有效性和魯棒性。

4.1 修改的IEEE 5節點交直流系統

為驗證所提基于HEM的交直流潮流求解算法的準確性和有效性，本文在Matlab（版本 8.3.0.532，R2014a）平臺上開發了所提算法的潮流計算程序，并以修改的IEEE 5節點交直流系統為例進行分析、驗證，該系統拓撲結構如圖6所示。

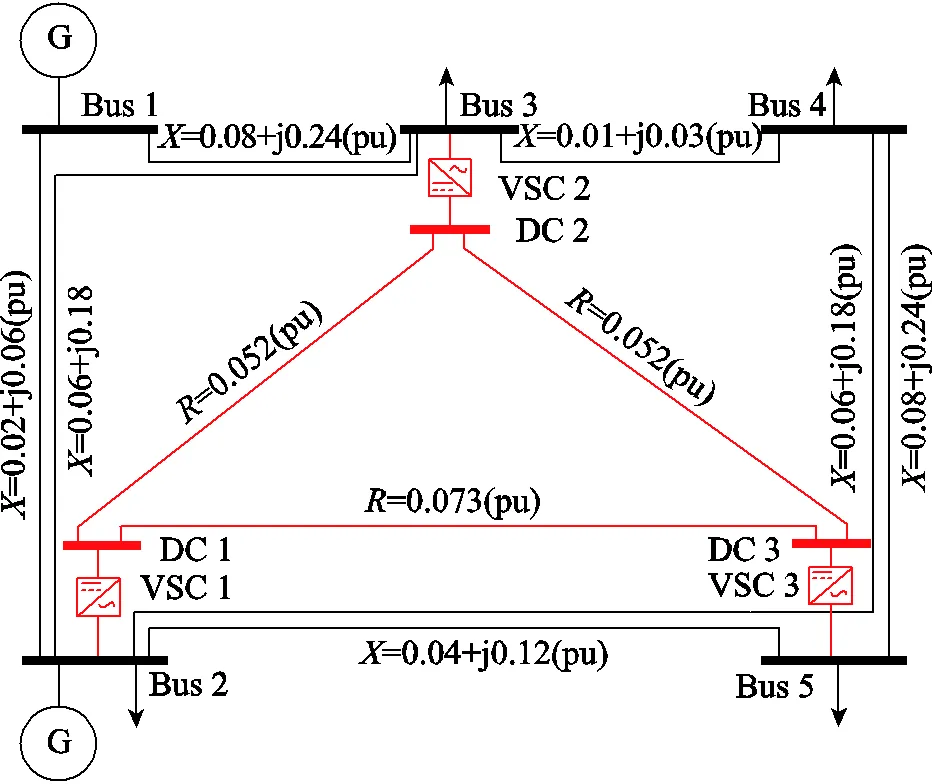
圖6 修改的IEEE 5交直流測試系統

圖6所示的交直流混合輸電網絡由5節點交流輸電網絡和3端直流輸電網絡構成，其交流和直流額定功率均為100MV·A，交流母線額定電壓為345kV。圖6中VSC換流站參數均相同，分別為tf=0.001 5+j0.112 1(pu)，c=0.000 1+j0.164 28(pu)，f=j0.088 7(pu)；直流母線額定電壓為345kV；潮流收斂閾值=10-4；換流站控制方式及參數見表1。

表1 IEEE 5節點交直流系統VSC換流站初始運行參數

Tab.1 Initial operation parameters of VSC in IEEE 5 AC-DC hybrid test system

4.1.1 算法準確性驗證

由3.4節電力系統交直流潮流的全純嵌入算法流程圖，計算交直流潮流需先進行交流側潮流計算，求取交流電壓冪級數系數見表2。

表2 IEEE 5節點交直流系統交流側節點電壓冪級數系數

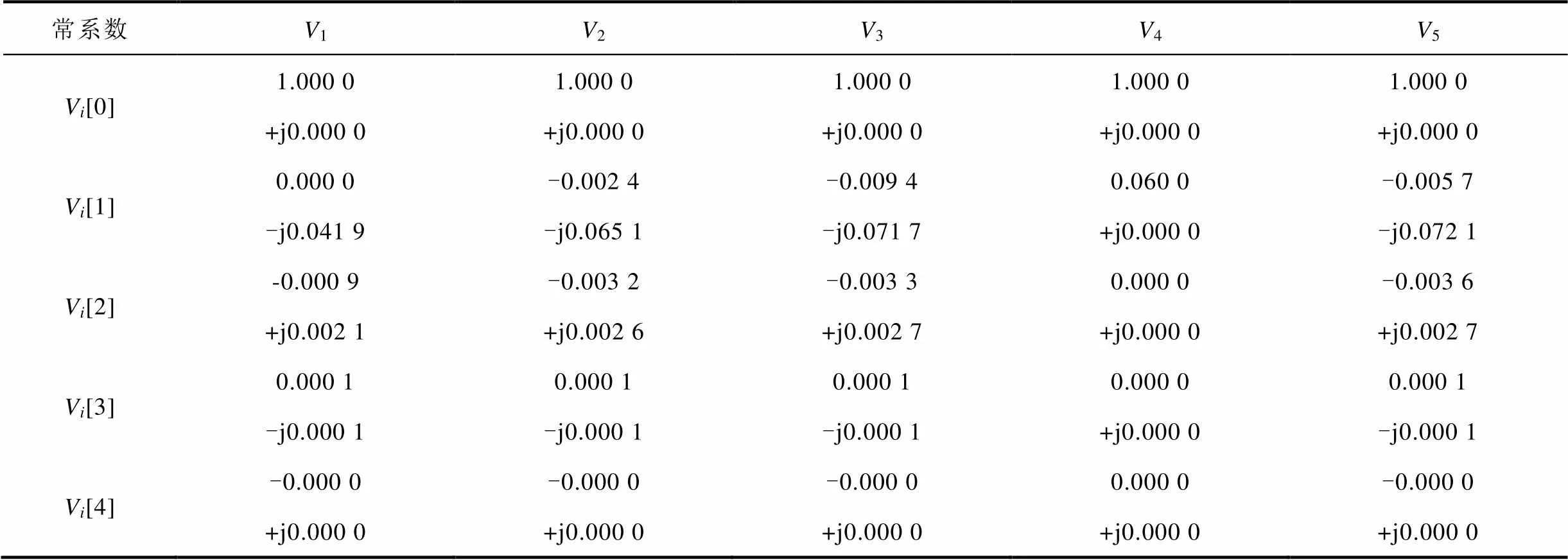
Tab.2 Power series coefficients of voltage in AC side of IEEE 5 AC-DC hybrid test system

表2中，第1行是各節點電壓冪級數0階的系數1[0]～5[0]，第2行是各節點電壓冪級數1階的系數1[1]～5[1]，將各節點電壓函數的0階與1階系數代入式（9）并令=1，求得1階冪級數對應的交流節電壓值分別為1=1.000 0-j0.041 9(pu)、2=0.997 6-j0.065 1(pu)、3=0.990 6-j0.071 7(pu)、4=1.060 0-j0.000(pu)、5=0.994 3-j0.072 0(pu)，對應的系統最大功率不平衡量Δmax=0.031 1(pu)，顯然不滿足所設定的收斂條件，應繼續計算更高階電壓冪級數系數，以提高潮流精度，圖7給出了冪級數階數與系統有功不平衡量之間關系。

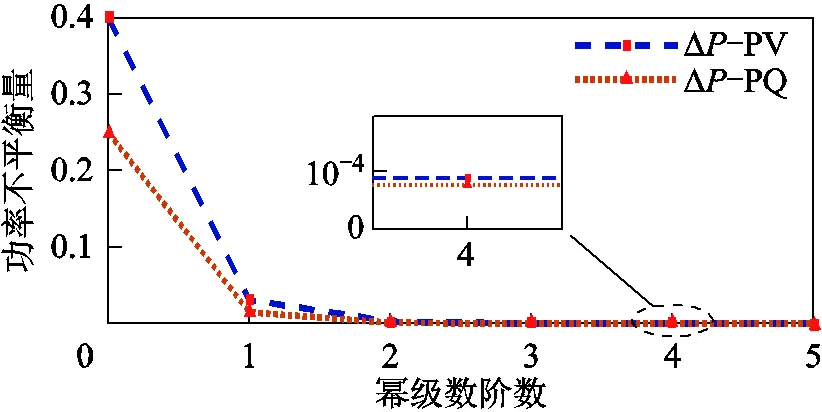
圖7 冪級數階數與功率不平衡量關系

由圖7可知，隨著冪級數階數增加，系統功率不平衡量隨之減小，通過求取高階冪級數系數可得系統高精度潮流解，本算例中僅需4階冪級數即可滿足收斂條件，完成交流側潮流計算。

確定交流側潮流分布后，需將交流PCC節點潮流信息傳遞至直流側，此時PCC節點電壓與節點功率可視為定值，依據圖1所示換流站等效電路分別計算換流母線電壓c、換流站損耗loss等相關換流站數據，并求取各直流節點有功功率dci，然后進行直流側潮流計算，直流側各節點電壓冪級數系數見表3。

表3 IEEE 5節點交直流系統直流側節點電壓冪級數系數

Tab.3 Power series coefficients of voltage in DC side of IEEE 5 AC-DC hybrid test system

表3給出了直流節點的電壓冪級數0～3階系數，將其代入式（20）求得各節點電壓標幺值為dc1=1.007 9(pu)、dc2=1.000 0(pu)、dc3=0.997 7(pu)，并校驗此時直流網絡功率不平衡量Δdc，經計算直流網絡功率不平衡量的最大值Δdc=4.518×10-5(pu)。因此，在實際計算中僅需計算出3階冪級數即可滿足收斂條件，實現直流側潮流的準確計算。

根據直流側潮流計算結果更新交流側PCC節點功率，再次計算交流側潮流，如此交替計算，直至功率不平衡量小于設定閾值，求得交直流系統潮流分布。將所得潮流計算結果與MATACDC計算結果進行對比，結果見表4和表5。

表4 IEEE 5節點交直流系統交流側電壓計算結果對比

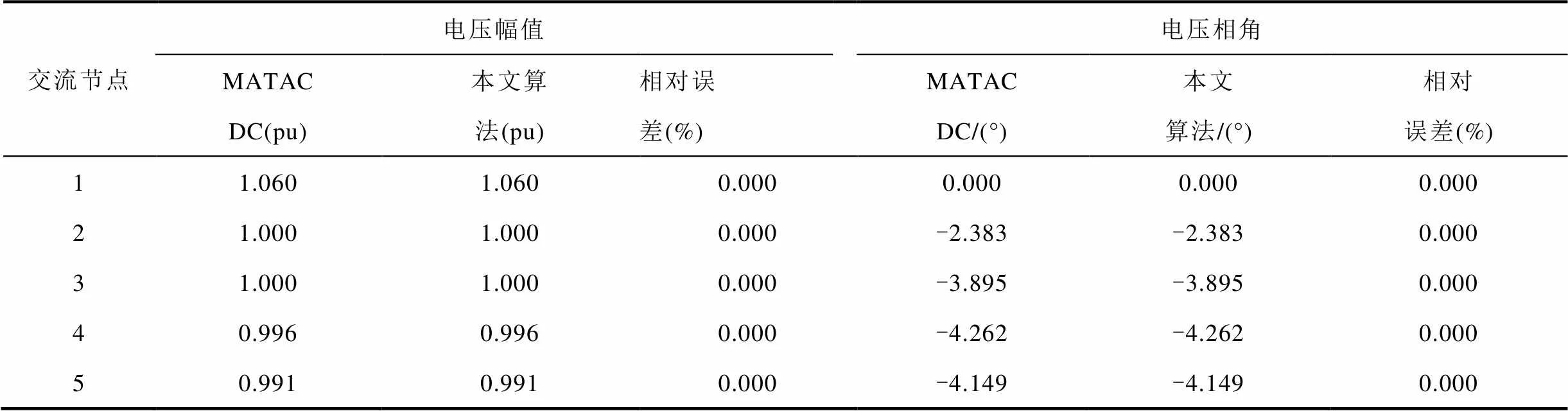
Tab.4 Comparison of the calculated voltages in AC side of IEEE 5 AC-DC hybrid test system

表5 IEEE 5節點交直流系統直流側潮流計算結果對比

Tab.5 Comparison of the calculated power flow in DC side of IEEE 5 AC-DC hybrid test system

由表4和表5可知：利用本文所提方法計算修改的IEEE 5節點交直流系統潮流結果與MATACDC的計算結果完全一致，驗證了本文所提電力系統交直流潮流的全純嵌入計算方法可實現交直流系統潮流的準確求解。

4.1.2 VSC換流站控制方式轉換功能驗證

為驗證所提算法可實現VSC換流站控制方式轉換的功能，本節對IEEE 5節點交直流系統的換流站控制方式進行切換，并將切換后的潮流計算結果與MATACDC進行對比，結果見表6。

表6 VSC換流站控制方式轉換前后潮流計算誤差對比

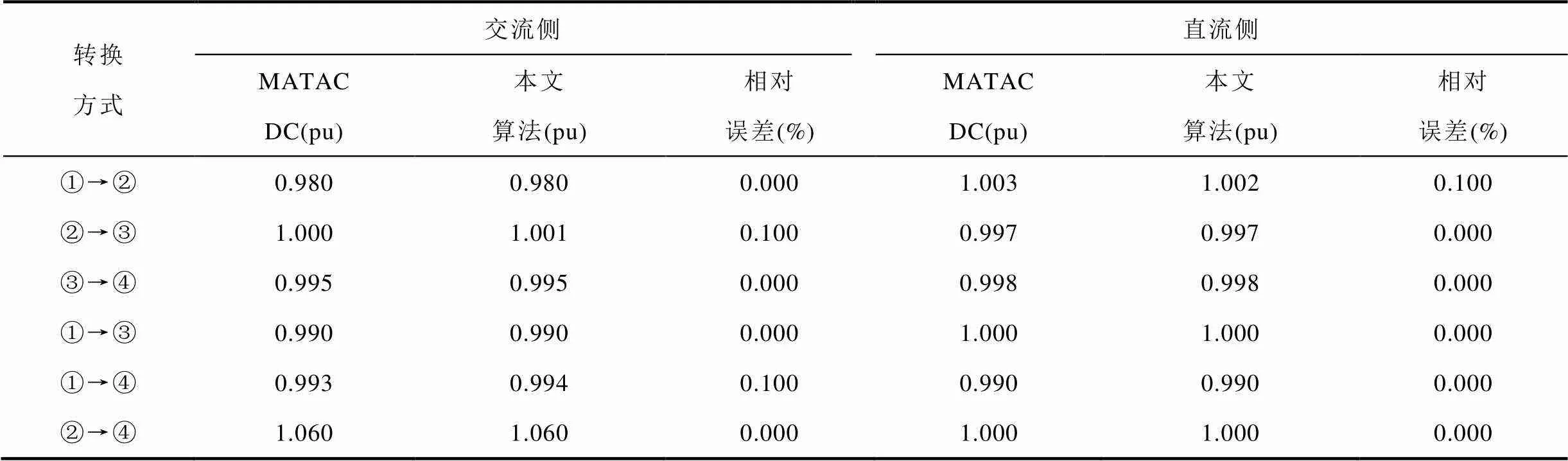
Tab.6 Comparison of calculation errors before and after VSC control mode switching

由表6可知：所提方法計算的交直流節點電壓幅值與MATACDC的結果一致，二者最大相對誤差僅為0.1%，有效驗證了所提基于HEM的交直流潮流求解算法可實現不同控制方式下交直流潮流的準確計算。

4.2 RTS-96多端交直流互聯系統

本節將所提的交直流潮流全純嵌入計算方法應用到拓撲結構更為復雜的RTS-96多端交直流互聯系統中，以驗證所提方法的通用性和有效性。該多端交直流系統由三個交流系統子區域和兩個直流網絡構成，其系統網絡結構如圖8所示。

4.2.1 準確性驗證

本節將所提基于HEM的交直流潮流求解算法與MATACDC所得潮流結果進行對比，按相對誤差百分比降序排列，圖9和圖10為交流側前10個具有最大相對誤差的節點電壓，表7為直流側潮流結果對比。

由圖9和圖10可知：基于HEM的交直流潮流求解算法所得的交流側節點電壓幅值和相角與MATACDC的計算結果一致，滿足潮流準確度要求。

圖8 RTS-96多端交直流互聯系統示意圖

圖9 RTS-96交直流系統交流側節點電壓幅值對比

圖10 RTS-96交直流系統交流側節點電壓相角對比

由圖9、圖10和表7的潮流計算結果可知：采用本文所提交直流潮流求解算法得到的RTS-96系統潮流計算結果與MATACDC計算結果完全一致，由此驗證了本文所提潮流求解算法同樣適用于拓撲結構較復雜的多分區、多端交直流互聯系統潮流計算。

表7 RTS-96交直流系統直流側潮流計算結果對比

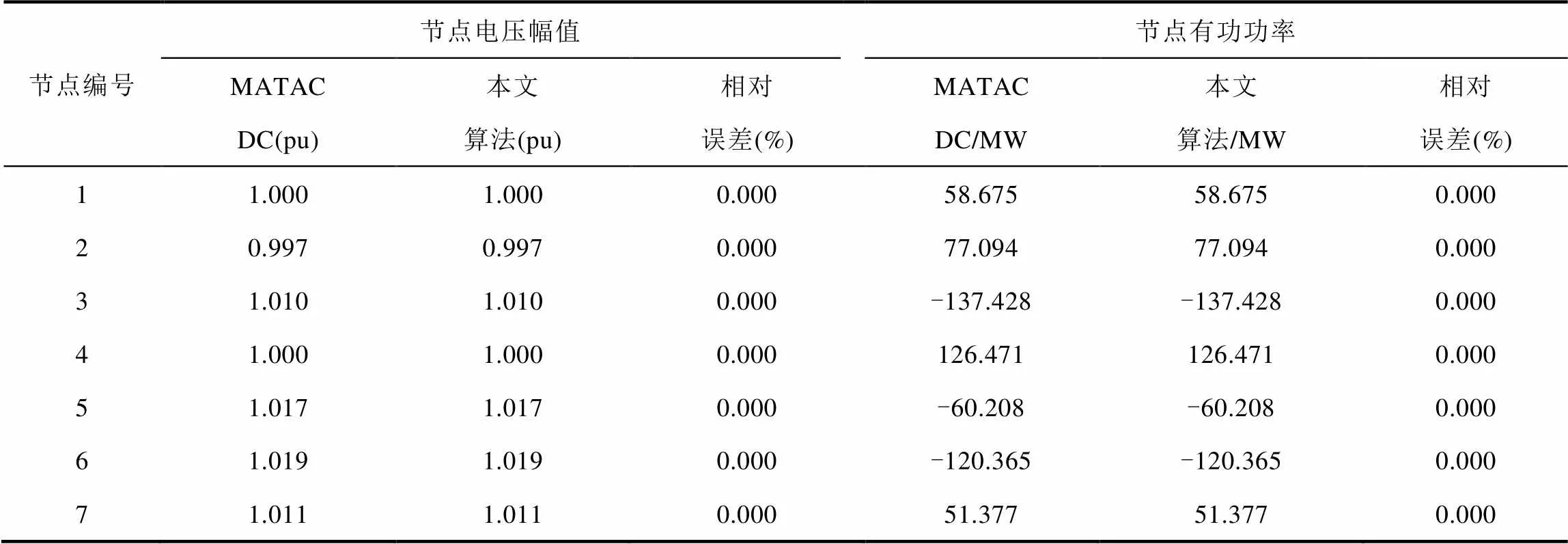
Tab.7 Comparison of power flow results in DC side of RTS-96 AC-DC hybrid test system

4.2.2 換流站控制策略轉換

參考文獻[15]，本節設置換流母線電壓幅值上、下限分別為c,min=0.850(pu)，c,max=1.150(pu)。2號和7號換流器無功類控制方式均為定功率控制，若交流203和217節點無功負荷分別增大至180Mvar和230Mvar，此時該節點無功支撐能力不足，交流節點203和217的電壓幅值分別為0.868(pu)和0.917(pu)，換流母線電壓分別為0.742(pu)和0.823(pu)，電壓越下限。將換流站控制方式由定無功功率控制改為定交流電壓控制，交流電壓設定值為1.000(pu)。轉換前后交流系統PCC節點電壓幅值如圖11所示，各換流母線電壓幅值如圖12所示。

圖11 換流站控制策略轉換前后交流PCC節點電壓對比

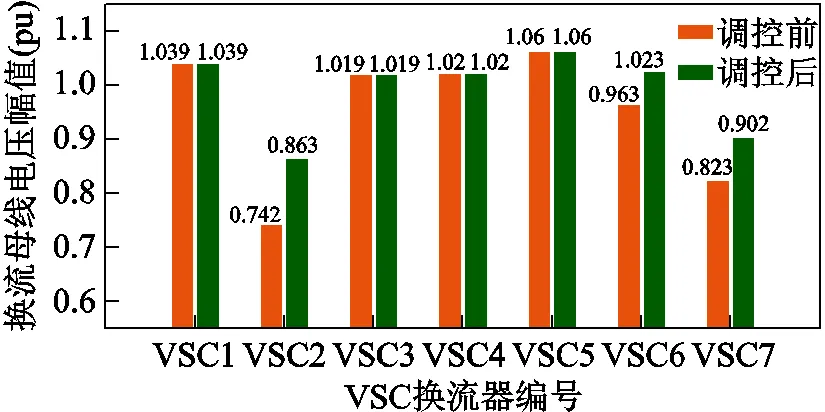
圖12 換流母線電壓越下限控制策略轉換前后對比

由圖11和圖12分析可知，VSC換流站交流側控制方式由定無功功率控制轉變為定交流電壓控制后，VSC換流站為交流PCC提供了充足的無功功率，顯著改善了交流側節點電壓。由于交流PCC節點電壓的提高，換流母線電壓也相應的提高，進而使得換流器在額定電壓范圍內安全運行。

若交流節點203和217無功負荷功率分別繼續增加100Mvar和150Mvar，此時PCC節點PCCs不變，換流站注入交流系統PCC的無功功率PCCs持續增加，進而導致c越上限c,max。為維持換流站的穩定運行，需將交流側控制方式由定交流電壓控制轉換為定無功功率控制，無功功率設定值為221Mvar和306Mvar，控制方式轉換前后換流母線電壓幅值如圖13所示。

由圖13可知，換流站控制方式由定交流電壓控制轉變為定無功功率控制，限制了換流站無功功率注入量，有效解決了換流母線電壓越上限問題。上述結果進一步驗證了所提方法可實現換流器控制策略的靈活轉換。

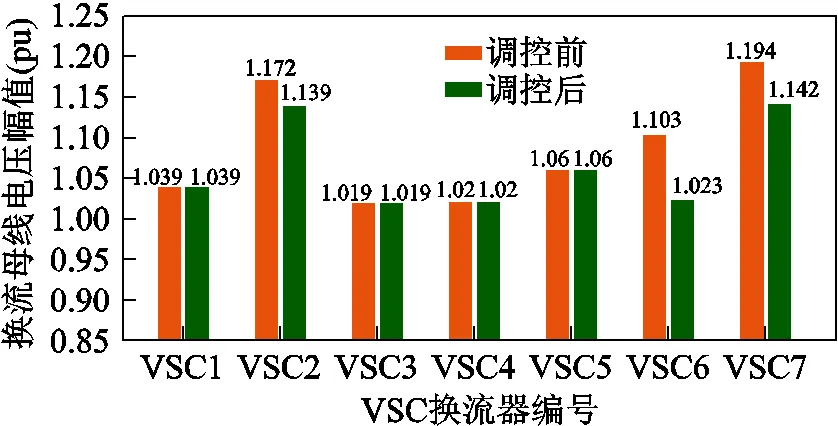
圖13 換流母線電壓越上限控制策略轉換前后對比

4.2.3 計算效率對比

為驗證所提算法的計算效率，將本文所提基于HEM的交直流潮流求解算法與MATACDC的潮流計算耗時進行對比（處理器Intel(R) Core(TM) i7-4500U CPU@1.80GHz，內存4.00GB），結果見表8。

表8 RTS-96交直流系統不同潮流算法計算耗時對比

Tab.8 Computational time comparison in RTS-96 AC-DC hybrid test system with different methods

由表8中結果分析可知：當交直流交替計算收斂精度均為10-4時，本文所提基于HEM的交直流全純潮流求解算法與MATACDC的交替計算次數均為4次，但所提算法計算耗時僅為0.25s，計算速度較MATACDC提高4.56倍。其原因為：本文所提基于HEM的交直流潮流求解算法在計算交流側和直流側潮流時，用于冪級數求解的線性方程組對應系數矩陣為常數陣，與傳統NR法相比，交直流潮流信息交互的大循環和節點電壓修正的小循環引起的節點功率變化均不會對該矩陣產生影響，所以僅需進行一次求逆運算即可滿足交替計算需求，有效降低了計算負擔。因此，本文所提基于HEM的交直流全純潮流求解算法具有更高的計算效率。

進一步通過不斷增加系統的負荷水平來測試所提方法的魯棒性，不同負荷水平下兩種算法的耗時對比結果見表9。

表9 不同負荷水平下兩種算法的耗時對比

Tab.9 Comparisons of computational time with two algorithms under different load levels

由表9可知：①在滿足相同潮流收斂條件下，所提基于HEM的交直流潮流求解算法收斂用時更少，具有更高的計算效率；②當負荷增加至一定程度，系統處于重載時，易造成NR法的Jacobi矩陣奇異，導致潮流無法收斂，而所提交直流潮流求解算法不會出現類似矩陣奇異問題，故所提算法在8次交替后仍可準確計算出交直流系統的潮流解，驗證了所提方法具有較強的魯棒性。

4.3 波蘭電網3012wp交直流測試系統

本節進一步以圖14所示波蘭電網3012wp交直流測試系統為例，驗證所提算法計算大規模交直流系統潮流的魯棒性和有效性。波蘭電網3012wp交直流測試系統，由原波蘭電網3012wp測試系統和一個4端直流電網構成，各直流換流站接入位置如圖14所示，換流站控制方式及運行參數詳見表10。

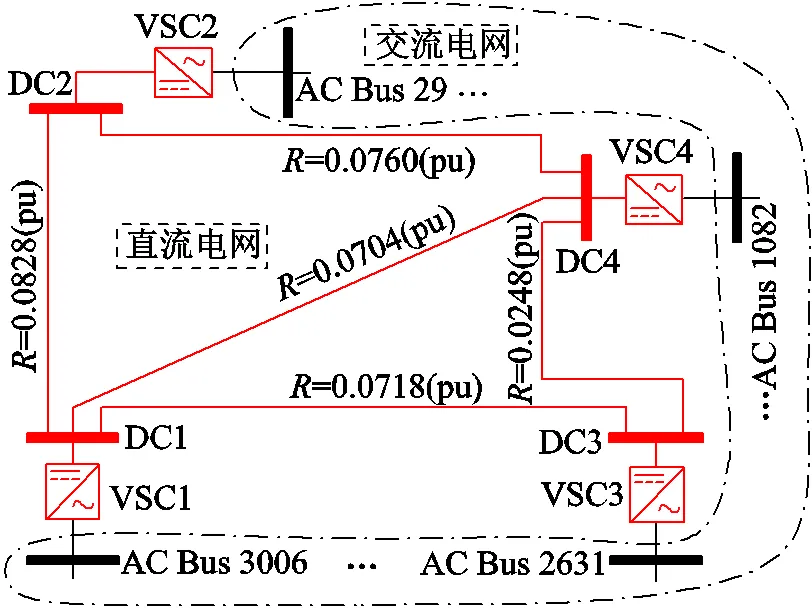
圖14 波蘭電網3012wp交直流測試系統示意圖

表10 VSC換流站初始運行參數

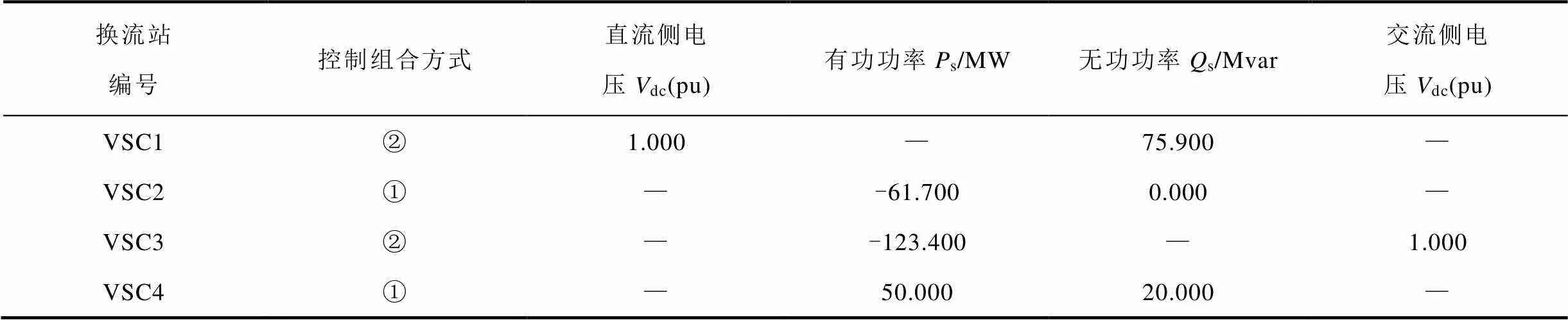
Tab.10 Initial operating parameters of VSC converter station in Polish 3012wp power grid

采用本文所提基于HEM的交直流潮流求解算法對該交直流測試系統進行潮流計算，按相對誤差百分比降序排列，表11給出了交流側前10個具有最大有功計算誤差的節點，直流側各節點潮流計算結果見表12。

表11 波蘭3012wp交直流系統交流側潮流計算結果

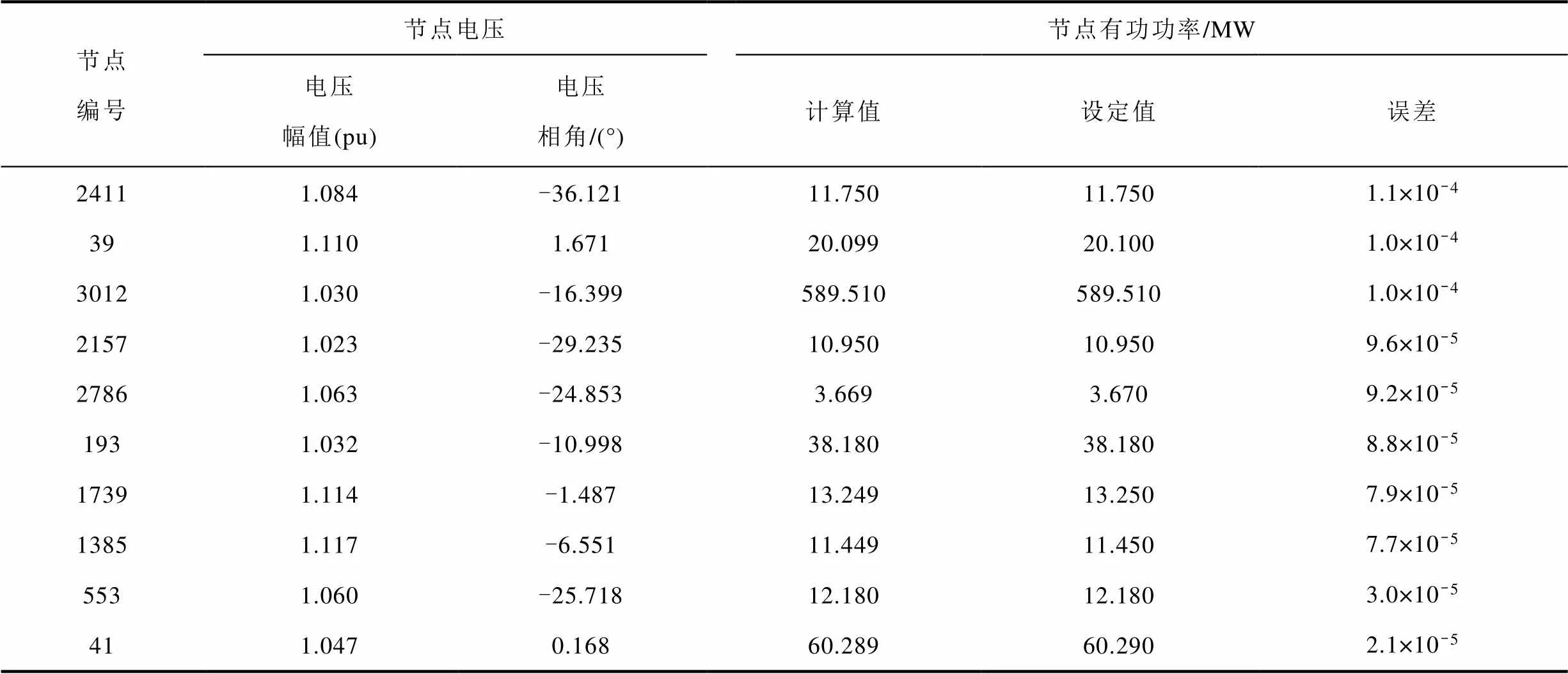
Tab.11 Power flow results of AC side in Polish 3012wp power grid

表12 波蘭3012wp交直流系統直流側潮流計算結果

Tab.12 Power flow results of DC side in Polish 3012wp power grid

由表11和表12的潮流計算結果可知：本文所提基于HEM的交直流潮流求解算法所得交直流測試系統的潮流最大功率不平衡量僅為1.1′10-4MW，驗證了所提算法在計算大規模交直流系統潮流時具有較高的計算精度。

表13進一步對比了本文所提算法與MATACDC在求解該系統的計算耗時，由表中結果可知，本文所提算法僅需1.69s即可準確計算出該系統潮流，而MATACDC計算結果不收斂。

表13 波蘭3012wp交直流系統潮流計算耗時對比

Tab.13 Comparison of time consumption for power flow calculation in the Polish 3012wp power grid

上述結果表明：所提基于HEM的交直流潮流求解算法，不僅適用于較小規模交直流系統的潮流計算，對大規模交直流互聯電網的潮流計算也展現出良好的計算精度、計算效率和魯棒性。

5 結論

本文提出一種基于HEM的交直流潮流計算方法，并通過修改的IEEE 5節點交直流系統、RTS-96交直流系統和波蘭電網3012wp交直流測試系統進行分析、驗證，結果表明：

1）所構建的全純交流潮流模型、全純直流潮流模型及換流站全純控制模型合理、可行，可實現基于HEM的交直流潮流快速、準確計算。

2）所構建VSC換流站全純控制模型，可準確、有效地計及不同控制方式間的相互轉換，實現基于HEM的多種控制方式下的交直流潮流準確計算，具有較強的通用性。

3）所提基于HEM的交直流潮流計算方法不依賴初值便可快速、準確地計算出交直流系統的潮流，且相對NR法更具有較強的魯棒性。

4）所提基于HEM的交直流潮流計算方法為交直流電網的潮流計算提供了新思路，也為電力系統運行調度和研究人員進行規劃運行、穩定性分析、可靠性評估等提供了新的潮流計算工具。

需要指出的是，盡管本文所提方法可實現電力系統交直流潮流的準確計算，但現階段VSC換流站全純控制模型主要是主從控制模式，未對換流站下垂控制模式的全純模型構建進行深入研究。而構建VSC換流站全純下垂控制模型，完善基于HEM的交直流潮流求解算法中VSC換流站各項全純控制模型，將是本文后續研究的重點。

[1] 朱介北, 周小堯, 曾平良, 等. 英國交直流輸電網規劃方法及對中國電網規劃的啟示[J]. 全球能源互聯網, 2020, 3(1): 59-69.

Zhu Jiebei, Zhou Xiaoyao, Zeng Pingliang, et al. UK AC-DC power grid planning method and its implications for China power grid planning[J]. Global Energy Internet, 2020, 3(1): 59-69.

[2] 駱悅, 姚駿, 張田, 等. 大規模風電直流外送系統單極閉鎖場景下送端系統協調控制策略[J]. 電工技術學報, 2019, 34(19): 4108-4118.

Luo Yue, Yao Jun, Zhang Tian, et al. Coordinated control strategy of sending-end system in the single-pole blocking scenario of large-scale wind power DC transmission system[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4108-4118.

[3] 李巖, 滕云, 冷歐陽, 等. 含多端柔性直流互聯的交直流電力系統靜態安全分析[J]. 電力系統自動化, 2019, 43(10): 155-163.

Li Yan, Teng Yun, Leng Ouyang, et al. Static security analysis of AC-DC power system with multi-terminal flexible DC interconnection[J]. Automation of Electric Power Systems, 2019, 43(10): 155-163.

[4] 李國慶, 邊競, 王鶴, 等. 適用于直流電網的環流式線間直流潮流控制器[J]. 電工技術學報, 2020, 35(5): 1118-1127.

Li Guoqing, Bian Jing, Wang He, et al. Circulating line-to-line DC power flow controller for DC power grids[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1118-1127.

[5] 周曉風, 付艷, 崔晨, 等. 提高分接開關可靠性的直流輸電控制策略優化[J]. 電氣技術, 2020, 21(9): 54-58.

Zhou Xiaofeng, Fu Yan, Cui Chen, et al. The optimization of high voltage direct current control strategy to improve on-load tap changer reliability[J]. Electrical Engineering, 2020, 21(9): 54-58.

[6] 王浩翔, 趙冬梅, 陶然, 等. 基于分解的多目標進化算法的含MMC-HVDC交直流混合系統最優潮流研究[J]. 電工技術學報, 2020, 35(17): 3691-3702.

Wang Haoxiang, Zhao Dongmei, Tao Ran, et al. Research on optimal power flow of MMC-HVDC AC-DC hybrid system based on decomposition-based multi-objective evolutionary algorithm[J]. Transac-tions of China Electrotechnical Society, 2020, 35(17): 3691-3702.

[7] 陳厚合, 黃亞磊, 姜濤, 等. 含VSC-HVDC的交直流系統電壓穩定分析與控制[J]. 電網技術, 2017, 41(8): 2429-2438.

Chen Houhe, Huang Yalei, Jiang Tao, et al. Voltage stability analysis and control of AC-DC system with VSC-HVDC[J]. Power System Technology, 2017, 41(8): 2429-2438.

[8] 杜萍靜, 楊明, 曹良晶, 等. 含電壓源換流器交直流系統的仿射潮流算法[J]. 電工技術學報, 2020, 35(5): 1106-1117.

Du Pingjing, Yang Ming, Cao Liangjing, et al. Affine power flow algorithm for AC-DC system with voltage source converter[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1106-1117.

[9] 鄭超, 周孝信, 李若梅, 等. VSC-HVDC穩態特性與潮流算法的研究[J]. 中國電機工程學報, 2005, 25(6): 1-5.

Zheng Chao, Zhou Xiaoxin, Li Ruomei, et al. Study on VSC-HVDC steady-state characteristics and power flow algorithm[J]. Proceedings of the CSEE, 2005, 25(6): 1-5.

[10] Lei Jingting, An Ting, Du Zhengchun, et al. A general unified AC-DC power flow algorithm with MTDC[J]. IEEE Transactions on Power Systems, 2017, 32(4): 2837-2846.

[11] Beerten J, Cole S, Belmans R. Generalized steady-state VSC MTDC model for sequential AC-DC power flow algorithms[J]. IEEE Transactions on Power Systems, 2012, 27(2): 821-829.

[12] 鄭超, 盛燦輝. 含VSC-HVDC的交直流混合系統潮流統一迭代求解算法[J]. 中國電力, 2007(7): 65-69.

Zheng Chao, Sheng Canhui. A uniform iterative algorithm for power flow solution of AC-DC hybrid system with VSC-HVDC[J]. China Electric Power, 2007(7): 65-69.

[13] 陳謙, 唐國慶, 王潯. 多端VSC-HVDC系統交直流潮流計算[J]. 電力自動化設備, 2005(6): 1-6.

Chen Qian, Tang Guoqing, Wang Xun. AC-DC power flow calculation for multi-terminal VSC-HVDC system[J]. Electric Power Automation Equipment, 2005(6): 1-6.

[14] Beerten J, Cole S, Belmans R. A sequential AC-DC power flow algorithm for networks containing multi-terminal VSC-HVDC systems[C]//IEEE PES General Meeting, Providence, RI, 2010: 1-7.

[15] Beerten J, Belmans R. Development of an open source power flow software for high voltage direct current grids and hybrid AC-DC systems: MATACDC[J]. IET Generation, Transmission and Distribution, 2015, 9(7): 966-974.

[16] 李雪, 劉燁, 姜濤, 等. 電力系統負荷裕度的并行計算方法研究[J]. 中國電機工程學報, 2019, 39(14): 5105-5117.

Li Xue, Liu Ye, Jiang Tao, et al. Research on the parallel calculation method of load margin in power system[J]. Proceedings of the CSEE, 209, 39(14): 5105-5117.

[17] Marcos T, Kamel S, Jurado F. Robust and efficient approach based on richardson extrapolation for solving badly-initialized/ill-conditioned power flow problems[J]. IET Generation Transmission & Distribution, 2019, 13(13): 3524-3533.

[18] Trias A. The holomorphic embedding load flow method[C]//IEEE Power and Energy Society General Meeting, San Diego, 2012: 1-8.

[19] Shruti R, Yang Feng, Daniel J, et al. The holomorphic embedding method applied to the power flow problem[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3816-3828.

[20] Muthu K, Yang Feng, Daniel T. PV bus modeling in a holomorphically embedded power-flow formulation[C]//North American Power Symposium (NAPS), Manhattan, KS, 2013: 1-6.

[21] Jonckheere EA, Ke NP. Complex-analytic theory of the-function*[C]//Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 1997: 366-371.

[22] Liu Chengxi, Wang Bin, Hu Fengkai, et al. Online voltage stability assessment for load areas based on the holomorphic embedding method[J]. IEEE Transactions on Power Systems, 2018, 33(4): 3720-3734.

[23] 徐經民, 徐在德, 童超. 基于模糊下垂控制的VSC-HVDC交直流系統潮流計算方法[J]. 電力系統保護與控制, 2019, 47(20): 50-57.

Xu Jingmin, Xu Zaide, Tong Chao. VSC-HVDC AC-DC system power flow calculation method based on fuzzy droop control[J]. Power System Protection and Control, 2019, 47(20): 50-57.

[24] 陳厚合, 李國慶, 姜濤. 控制方式轉換策略下的改進交直流系統潮流算法[J]. 電網技術, 2011, 35(8): 93-98.

Chen Houhe, Li Guoqing, Jiang Tao. Improved AC-DC power flow algorithm under control mode switching strategy[J]. Power System Technology, 2011, 35(8): 93-98.

[25] 劉英培, 解賽, 梁海平, 等. 計及換流站間電壓誤差的VSC-MTDC系統自適應下垂控制[J]. 電工技術學報, 2020, 35(15): 3270-3280.

Liu Yingpei, Xie Sai, Liang Haiping, et al. Adaptive droop control of VSC-MTDC system considering voltage error between converter stations[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3270-3280.

A Holomorphic Embedded Method for Solving Power Flow in Hybrid AC-DC Power System

Jiang Tao Zhang Yong Li Xue Li Guoqing Chen Houhe

(Key Laboratory of Modern Power System Simulation and Control & Renewable Energy Technology Ministry of Education Northeast Electric Power University Jilin 132012 China)

In order to address the initial value selection and large calculation amount when Newton Raphson(NR) method is used to calculate AC-DC power flow, this paper proposes a holomorphic embedding method for AC-DC power flow calculation. Firstly, according to the construction principle of holomorphic function, the holomorphic AC-DC power flow model and converter station control model are constructed by embedding parameters. Then, based on the Taylor series expansion characteristics of the holomorphic function, the problem of solving nonlinear power flow equations is transformed into an explicit problem of implicit holomorphic functions. Moreover, according to the principle that the same power coefficient is equal, the power series coefficient of Taylor series expansion term is obtained, and the explicit holomorphic function is completed, and then the embedded parameters are assigned to realize the fast solution of AC-DC power flow. Finally, it is analyzed and verified through modified IEEE 5 node AC-DC system, RTS-96 AC-DC system and Polish power grid 3012wp AC-DC test system. The results show that the proposed method can quickly and accurately calculate the power flow of AC-DC power system without relying on the initial value, and has strong robustness, which provides a new idea for power flow calculation of large-scale AC-DC power grid.

AC-DC hybrid system, voltage source converter, holomorphic function, power flow calculation

10.19595/j.cnki.1000-6753.tces.201306

TM744

國家自然科學基金（52077029, U2066208, 52061635103）和國家重點研發計劃（2016YFB0900900）資助項目。

2020-09-29

2020-11-23

姜 濤 男，1983年生，博士，教授，博士生導師，研究方向為電力系統安全性和穩定性、可再生能源集成、綜合能源系統。E-mail：t.jiang@aliyun.com

李 雪 女，1986年生，博士，副教授，碩士生導師，研究方向為電力系統安全性與穩定性、電力系統高性能計算、電力市場。E-mail：xli@neepu.edu.cn（通信作者）

（編輯 赫蕾）