低開關頻率下基于MRAS的永磁同步電機無位置傳感器控制延時分析

翁 聰，周明磊，游小杰，郝瑞祥

（北京交通大學電氣工程學院，北京 100044）

0 引言

永磁同步電機（Permanent Magnet Synchronous Motor，PMSM）具有功率密度大、運行效率高、控制性能好等優點，在軌道交通、航空航天、伺服控制等領域得到了廣泛應用。永磁同步電機的控制需要獲得可靠的轉子位置信息，現多采用霍爾傳感器、光電編碼器、旋轉變壓器等機械式傳感器，增加了硬件成本及后期維護成本，降低了系統的可靠性。因此，永磁同步電機無位置傳感器控制的研究受到了國內外學者的廣泛關注。目前，常用的無位置傳感器控制方法分為零低速范圍內無位置傳感器控制方法和中高速范圍內無位置傳感器控制方法兩類。其中，零低速范圍內常用的方法有：高頻旋轉電壓信號注入法[1]、高頻脈振電壓信號注入法[2]和載波頻率成分法[3]等；中高速范圍內常用的方法有：模型參考自適應法[4]、擴展Kalman濾波器法[5]和滑模觀測器法[6]等。模型參考自適應法具有算法簡單、魯棒性強、參數估計易收斂、穩態性能優良等特點，在無傳感器控制領域得到了廣泛應用。

永磁同步電機無位置傳感器控制的關鍵是能夠準確辨識出永磁同步電機的轉子位置，然而數字控制中因為各種原因引起的系統延時將導致電機實際發出電壓的相位與期望相位之間存在偏差，該偏差會導致永磁同步電機轉子位置估算誤差增大，降低無位置傳感器控制性能。

針對數字控制中的延時問題，國內外學者已經有了許多研究。文獻[7]、文獻[8]在傳統采樣模式的基礎上，通過提高采樣率來減少采樣延時。文獻[9]從理論上分析了延時對電流PI調節器帶寬的影響，并提出了改進的電流采樣方法。文獻[10]提出了一種新的電流環時序，通過限制電壓輸出能力來消除計算延時。文獻[11]設計了一種改進型離散電流控制器，可以對延時進行補償。文獻[12]分析了延時對交流傳動控制系統穩定性的影響，提出了一種基于q軸電流誤差的延時補償方法。

當前，永磁同步電機無位置傳感器控制雖然是研究熱點，但是針對大功率永磁同步電機雙頻計算控制框架下的延時分析還較少。本文針對大功率永磁同步電機無位置傳感器控制延時問題進行了具體分析，確定了大功率永磁同步電機無位置傳感器控制中延時的具體大小，并且根據分析對延時進行了直接補償。

1 基于MRAS的PMSM無位置傳感器控制

1.1 PMSM的數學模型

本文的研究對象是一臺內置式永磁同步電機，在同步旋轉坐標系下，其定子電壓方程為

定子磁鏈方程為

電磁轉矩方程為

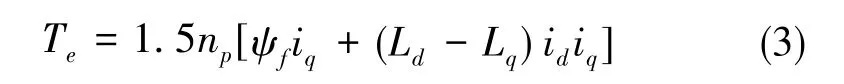
機械運動方程為

式（1）～式（4）中， ud、 uq分別為定子電壓d軸、q軸的分量，id、iq分別為定子電流d軸、q軸的分量，Rs為定子電阻，ψd、ψq分別為定子磁鏈 d軸、q軸的分量，Ld、Lq分別為d軸、q軸的電感，Te為電磁轉矩，np為電機極對數，ψf為永磁體磁鏈，J為轉動慣量，ωr為電角速度，ωm為機械角速度，B為阻尼系數，TL為負載轉矩。

1.2 基于MRAS的PMSM無位置傳感器控制策略

在MRAS中，常以永磁同步電機定子電流方程或者磁鏈方程為參考模型。本文采用定子電流方程為參考模型，永磁同步電機在同步旋轉坐標系下以定子電流作為狀態變量的狀態方程為

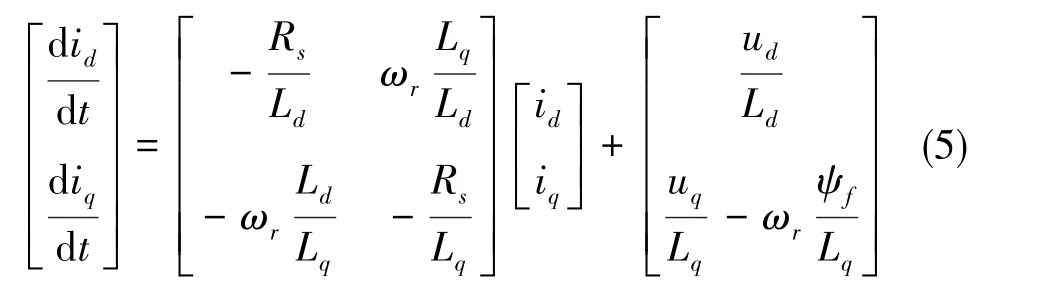
式（5）即為參考模型，根據式（5）可以建立對應的可調模型，然后根據參考模型和可調模型設計合適的自適應律（詳細推導可參考文獻[4]），最后基于Popov超穩定性理論確定自適應律為

轉子位置可通過對轉速進行積分得到

于是得到了基于定子電流的MRAS轉子位置估算系統框圖，如圖1所示。

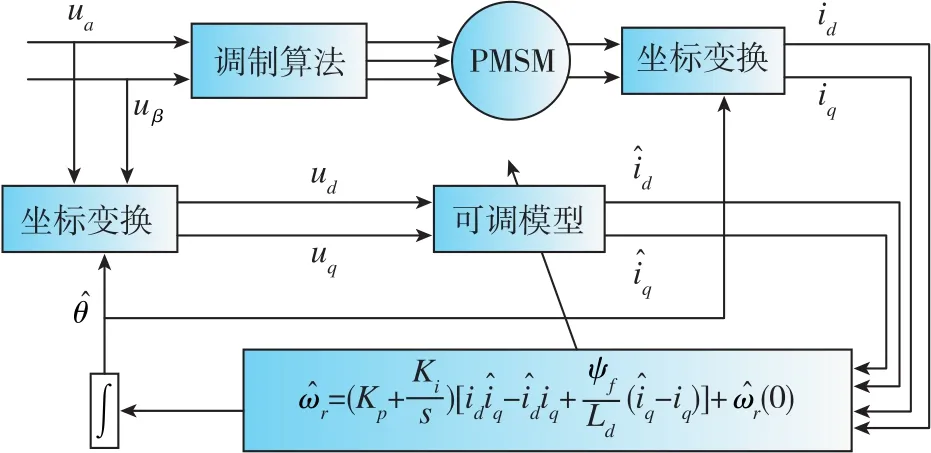
圖1 基于MRAS的PMSM轉子位置估算框圖Fig.1 Block diagram of PMSM rotor position estimation based on MRAS

2 大功率系統控制框架

在小功率系統中，因為其逆變器開關頻率很高，在全速度范圍內的載波比都可以保持在很高的水平，因此采用一種調制方法即可。而在大功率系統中，由于其電壓高、電流大的特點，其逆變器開關頻率最大為幾百赫茲，從而在中高速范圍內載波比維持在一個較低的水平，造成基波電壓誤差增大、相位延時和諧波增多等問題。因此，在大功率傳動系統中通常采用多模式調制策略。

本文采用的多模式調制策略如圖2所示，為了與逆變器開關頻率對應，電機轉速單位用赫茲表示。調制策略分為高載波比下的調制策略和低載波比下的調制策略兩個部分，即：在電機轉速低于20Hz的高載波比范圍內采用異步調制策略，此時調制頻率為300Hz；在電機轉速高于20Hz的低載波比范圍內采用同步調制策略，此時調制頻率隨著電機轉速的變化而變化。

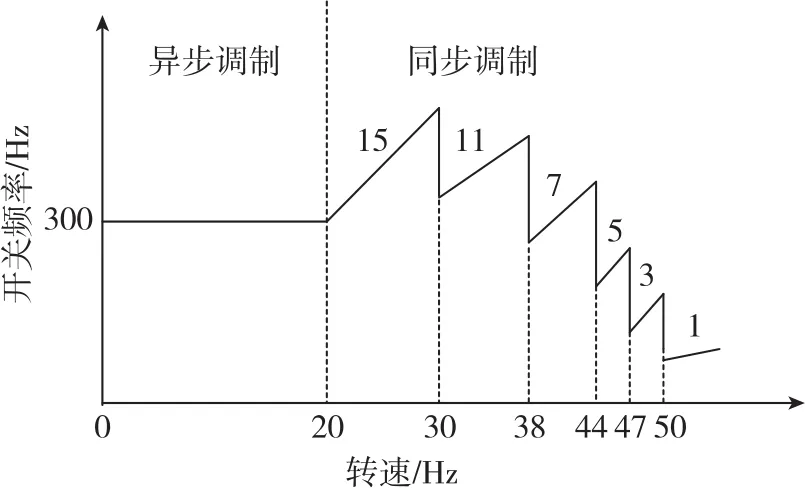
圖2 多模式調制策略示意圖Fig.2 Schematic diagram of multimode modulation strategy

由于調制部分計算頻率不固定，控制部分計算頻率固定不變，本文采用控制部分和調制部分分開的控制框架，如圖3所示。控制部分計算頻率固定為10kHz，電機進入方波工況前采用傳統矢量控制方案；進入方波工況后，由于輸出電壓不可調節，傳統的矢量控制方案失效，此時采用改進型矢量控制方案。控制部分和調制部分通過相角調節器連接。

圖3 大功率永磁同步電機控制框圖Fig.3 Control block diagram of high-power PMSM

相角調節器的結構原理圖如圖4所示。控制部分發出的轉子位置角θc減去調制部分上一拍坐標變換所用的電壓矢量角，差值通入P調節器，再將調節器輸出疊加到控制部分發出的電機轉速fr上，修正后的頻率信號通過調制算法中的積分器可以得到調制部分坐標變換所需的電壓矢量角θmod。

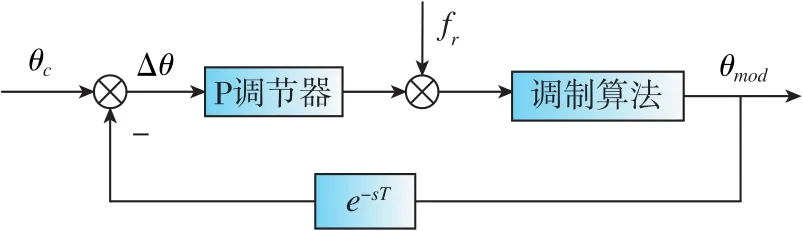
圖4 相角調節器結構原理圖Fig.4 Structure schematic diagram of phase angle regulator

3 延時分析

3.1 典型數字控制時序延時分析

在數字控制系統中，DSP計算延時和PWM輸出延時在系統延時中占據主導地位。

在小功率系統中，典型的電流采樣和PWM更新時序圖如圖5所示，包括采樣、計算、PWM更新和PWM輸出。圖5中，Ts為調制周期，Tc為計算延時，Tpwm為PWM輸出延時，Td為系統延時。在實際系統中，采樣和計算所用的時間可以忽略不計。

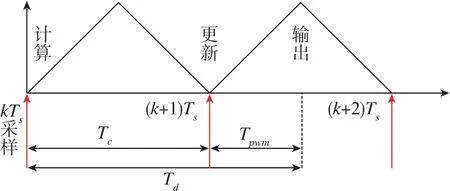
圖5 小功率系統中的電流采樣和PWM更新時序圖Fig.5 Sequence diagram of current sampling and PWM update in low-power system

計算延時即采樣時刻到PWM更新時刻的一個調制周期，有

文獻[13]推導出了PWM更新作用到系統上的延時為半個調制周期，即更新后的PWM等效在半個采樣周期后輸出。因此，PWM輸出延時為

故在典型數字控制系統中，總的系統延時為

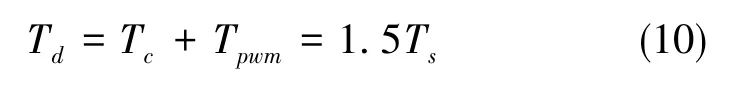
3.2 大功率系統延時分析

在大功率系統中，由于其逆變器開關頻率低，因此采用多模式調制策略。此時，為了準確發出指令電壓矢量，通常在控制部分與調制部分之間加入相角調節器，使調制部分坐標變換所用的電壓矢量角θmod能夠跟蹤上控制部分發出的轉子位置角θc。 由于轉子位置角可以由電機轉速積分得到，故圖4的相角調節器結構原理圖可以轉化為圖6所示的結構原理圖。

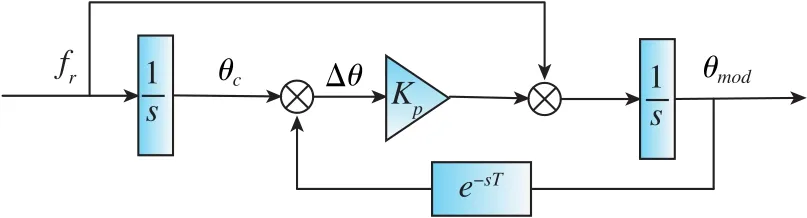
圖6 轉化后的相角調節器結構原理圖Fig.6 Structure schematic diagram of phase angle regulator after conversion

根據圖6所示的相角調節器結構，可以得到

故當PMSM轉速穩定不變時，圖6所示的系統穩態誤差為0，即調制部分坐標變換所用的電壓矢量角能夠無靜差地跟蹤上控制部分發出的轉子位置角。

大功率系統中的電流采樣和PWM更新時序圖如圖7所示，從電流采樣到PWM更新之間存在控制延時Tk和計算延時Tc。 由于調制頻率為幾百赫茲，而采樣頻率為幾千赫茲，故一個調制周期內進行多次電流采樣，PWM更新采用最近一次電流采樣計算結果。由于采樣頻率相較于調制頻率很高，控制延時Tk可以忽略不計，計算延時Tc可視為一個調制周期Ts。在不考慮相角調節器的作用時， 存在θmod（k）=θc（k）。 但是在大功率系統中由于相角調節器的相位跟蹤作用，調制部分坐標變換所用的電壓矢量角θmod（k+1）等于kTs時刻控制部分發給調制部分的轉子位置角θc（k）， 即控制部分超前給調制部分發出轉子位置角。因此，相角調節器的存在相當于補償了PWM計算到PWM更新時刻之間一個調制周期的計算延時。更新后的PWM脈沖信號等效在0.5Ts+（k+1）Ts發出PWM信號，即PWM輸出存在的0.5Ts延時。故低開關頻率下，由于相角調節器的相位跟蹤作用，總的系統延時為

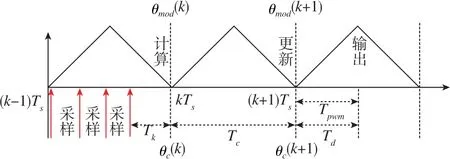
圖7 大功率系統中的電流采樣和PWM更新時序圖Fig.7 Sequence diagram of current sampling and PWM update in high-power system

低開關頻率下，在異步調制區域內，開關頻率不變，隨著電機轉速升高，延時導致的滯后角度增大。此時，滯后角度為

在同步調制區域內，開關頻率和轉速都發生變化，但同步調制中調制每次增加的角度固定。本文采用的同步調制方式為每次增加10°，此時的滯后角度為

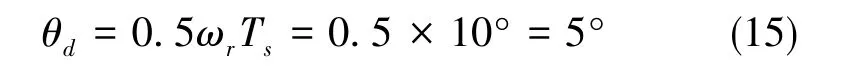
本文采用直接補償法，即在無位置傳感器估算出的轉子位置角的基礎上加上延時所導致的滯后角度 0.5ωrTs， 以此作為期望發出的電壓矢量角。

經過延時補償后的大功率永磁同步電機控制框圖如圖8所示。

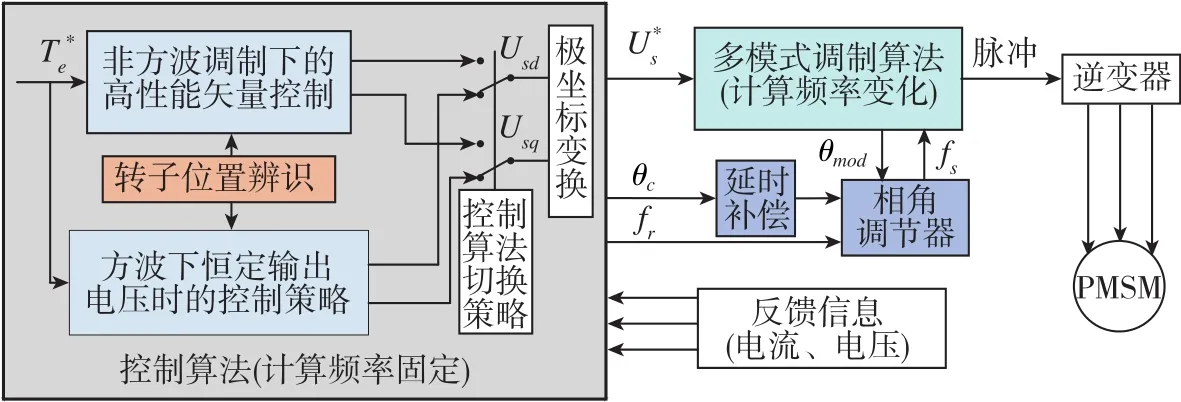
圖8 含有延時補償的大功率永磁同步電機控制框圖Fig.8 Control block diagram of high-power PMSM with time-delay compensation

4 仿真分析

4.1 延時分析仿真條件

為了驗證前面的理論分析結果，采用Matlab／Simulink軟件對本文所研究的基于MRAS的轉子位置估算方法進行仿真驗證，仿真用電機參數如表1所示。低開關頻率下采用多模式調制策略，即：中低速段采用異步調制、中高速段采用同步調制，分別分析異步調制區域內和同步調制區域內系統延時對基于MRAS的轉子位置觀測的影響。

表1 電機參數Table 1 Parameters of motor

4.2 延時補償前的仿真驗證

（1）異步調制區域內

仿真工況為：低開關頻率下，控制頻率為10kHz，開關頻率為300Hz，轉矩指令值為10N·m，電機分別穩定在10Hz、15Hz下運行，仿真結果如圖9所示。

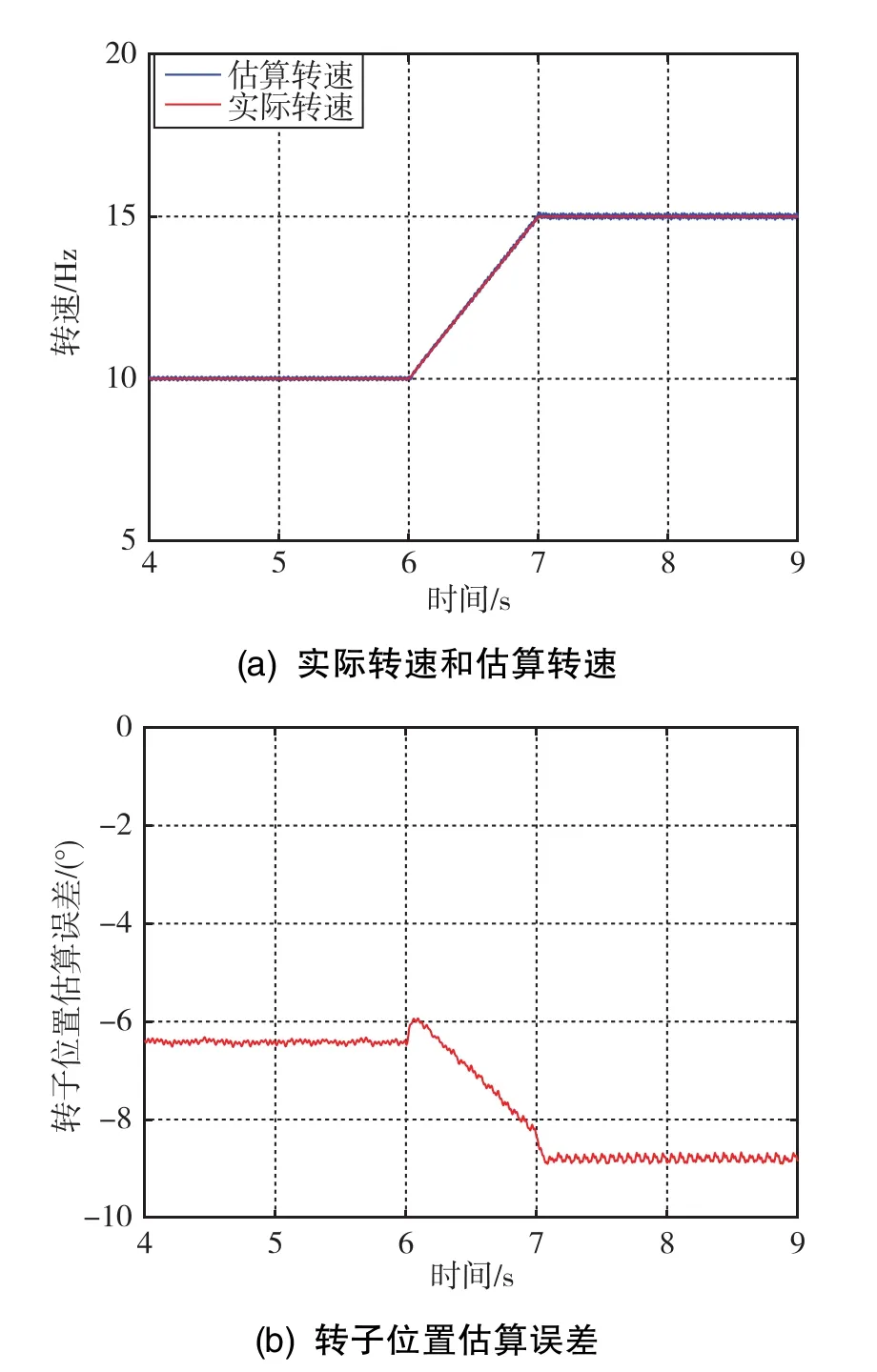
圖9 異步調制區域延時補償前的仿真結果Fig.9 Simulation results before time-delay compensation in asynchronous modulation area

由圖9（b）可知，在異步調制區域內，隨著電機轉速的升高，實際逆變器發出的電壓矢量滯后期望方向的角度增大，導致電機轉子位置估算誤差增大。按照3.2節的分析，可以得到以下結論：

當電機轉速為10Hz時，此時的轉子位置誤差為

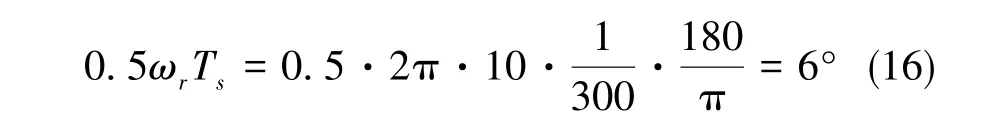
當電機轉速上升到15Hz時，此時的轉子位置誤差為

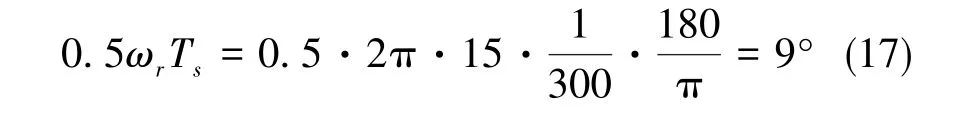
圖9（b）中，當轉速為10Hz時，轉子位置估算誤差為6°左右；當轉速為15Hz時，轉子位置估算誤差為9°左右，仿真結果與3.2節的分析一致。

（2）同步調制區域內

仿真工況為：低開關頻率下，控制頻率為10kHz，開關頻率隨轉速變化而變化，轉矩指令值為10N·m， 電機分別穩定在 25Hz、 35Hz、 40Hz、45Hz、50Hz、55Hz下運行，仿真結果如圖10所示。

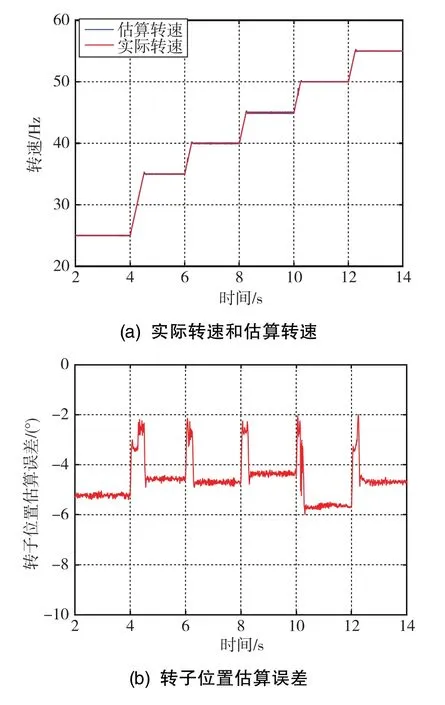
圖10 同步調制區域延時補償前的仿真結果Fig.10 Simulation results before time-delay compensation in synchronous modulation area

由圖10（b）可知，在同步調制區域內，轉子位置觀測誤差都在5°附近，仿真結果與3.2節的分析一致。

綜上所述，在大功率系統中，不管是在異步調制區域還是在同步調制區域，仿真結果都驗證了3.2節中大功率系統延時分析的準確性。由于延時的影響，轉子位置誤差最大可超過10°。為了提高永磁同步電機無位置傳感器控制的性能，有必要對系統延時進行補償。

4.3 延時補償后的仿真驗證

對3.2節中提出的延時補償方法進行仿真驗證，在控制部分傳遞給調制部分的電壓矢量角度的基礎上加上0.5ωrTs的延時補償，延時補償后進行仿真。

（1）異步調制區域內

仿真工況為：低開關頻率下，控制頻率為10kHz，開關頻率為300Hz，轉矩指令值為10N·m，電機分別穩定在10Hz、15Hz下運行，仿真結果如圖11所示。

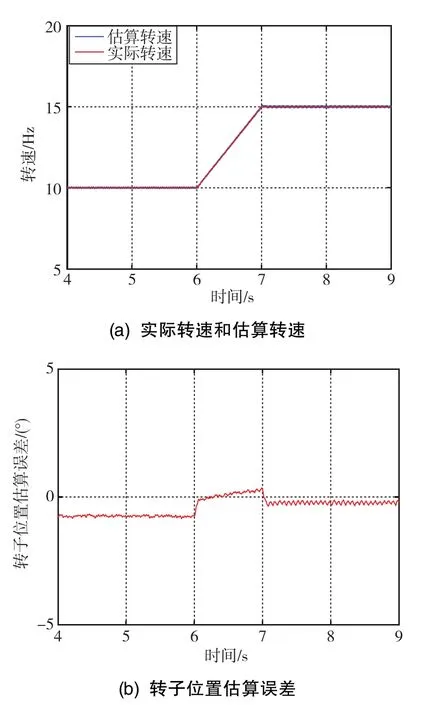
圖11 異步調制區域延時補償后的仿真結果Fig.11 Simulation results after time-delay compensation in asynchronous modulation area

由圖11（b）可知，在異步調制區域內，經過延時補償后，轉子位置觀測誤差都在0°附近，轉子位置觀測精度顯著提高。

（2）同步調制區域內

仿真工況為：低開關頻率下，控制頻率為10kHz，開關頻率隨轉速變化而變化，轉矩指令值為10N·m， 電機分別穩定在 25Hz、 35Hz、 40Hz、45Hz、50Hz、55Hz下運行，仿真結果如圖12所示。

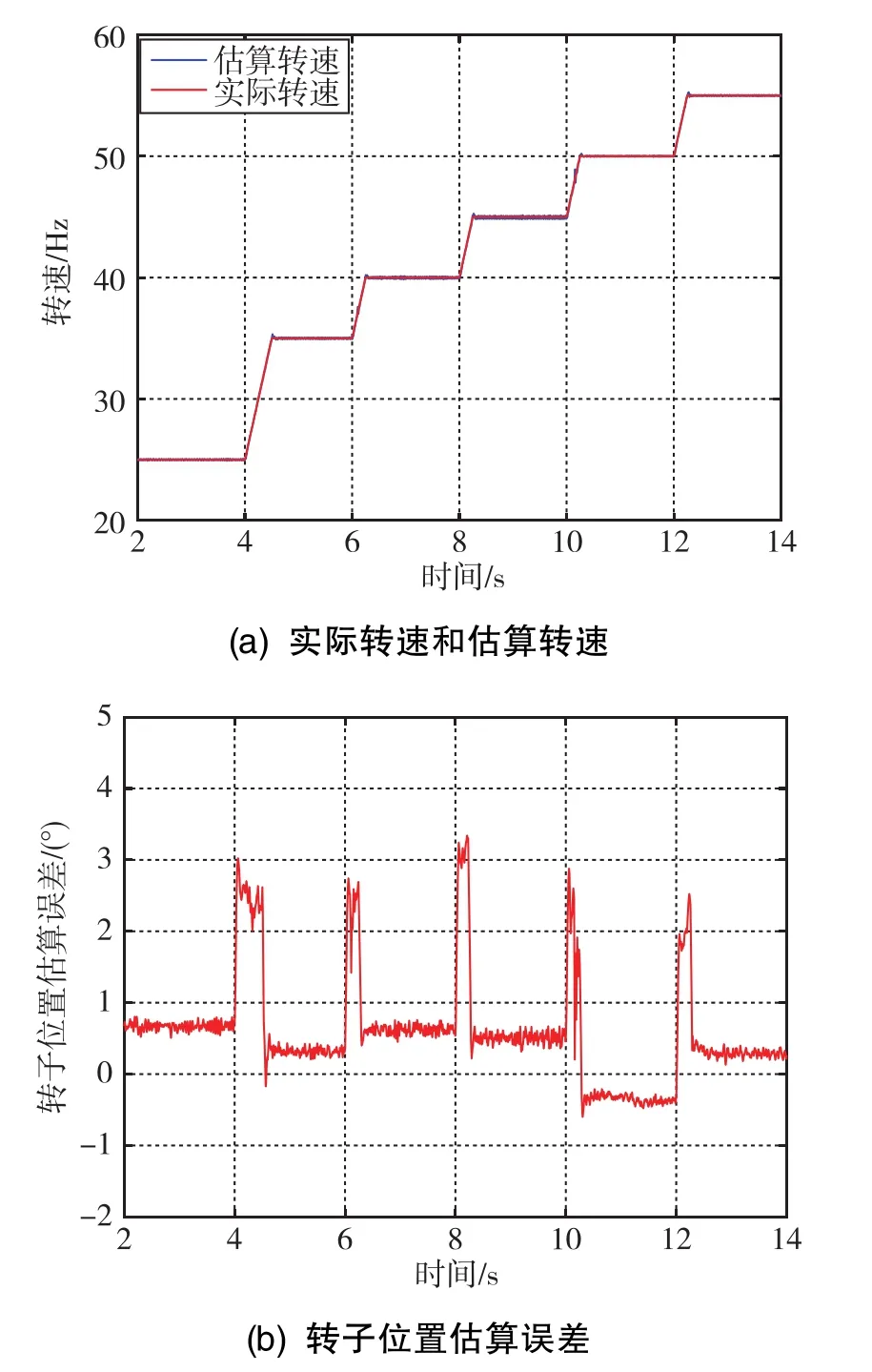
圖12 同步調制區域延時補償后的仿真結果Fig.12 Simulation results after time-delay compensation in synchronous modulation area

由圖12（b）可知，在同步調制區域內，經過延時補償后，轉子位置觀測誤差都在0°附近，轉子位置觀測精度顯著提高。

綜上所述，不管是在異步調制區域還是在同步調制區域，經過延時補償后，基于 MRAS的PMSM轉子位置觀測精度顯著提高，仿真結果驗證了3.2節中提出的直接延時補償方法的有效性。

5 結論

本文針對大功率永磁同步電機無位置傳感器控制系統延時進行研究，分析了大功率永磁同步電機雙頻計算控制框架下相角調節器在系統延時中的補償作用，確定了低開關頻率下系統延時的具體大小，并且根據理論分析進行延時補償，仿真結果驗證了本文關于大功率系統中延時分析的準確性。仿真結果顯示，經過延時補償后，在全速度范圍內，基于MRAS的永磁同步電機轉子位置觀測誤差都在0°附近，轉子位置觀測精度顯著提高。