世界優秀羽毛球男子單打后場技戰術行動與成績關系的研究

陳穗欽

1 前言

已有的對世界優秀羽毛球男子單打后場技戰術研究中，有兩個顯著的結論，一是在羽毛球前、中和后場，后場技戰術運用僅次于前場技戰術，二是后場不同技術使用率，從高到低排列依次是殺球、吊球、高遠球。

2012年倫敦奧運會林丹和李宗偉大戰中，林-李的后場球比例分別為25.88%和32.87%。都達到25%以上的占比，僅次于前場技戰術（王德平，2013）；2017年世錦賽八強比賽統計分析結果表明：優秀男子單打運動員擊球區域比例從高到低依次是前場51.8%、后場31.4%、中場16.8%（唐開悅，2018）。

對李宗偉和林丹30屆奧運會決賽研究表明在后場技術運用中按高低順序為：殺球占52%，吊球22%，高遠球12%（高偉華和王德平，2013）；單打選手林丹、李宗偉后場進攻技術的對比研究中殺球占71.1%和57.2%，吊球45%和52%，（姜來，2015）；2017年世錦賽八強比賽統計結果顯示后場技戰術使用率依次為：殺球40.5%、吊球30.1%、高遠球29.4%（唐開悅，2018）。

已有的研究揭示了后場技戰術運用的一些特征，如后場技戰術運用僅次于前場、各種技術使用頻率排列為殺球-吊球-高遠球。研究中存在的主要問題是：（1）多以個別的最優秀的運動員為研究對象，采用頻數的統計方法分析數據，由于樣本量較小，及研究者的意識，沒有采用集中趨勢和離散趨勢來分析數據，因此研究雖為描述性研究，但研究的規范性限制了對特征的深入描述；（2）沒有進一步探索羽毛球后場技戰術運用的因果關系，以及由此形成的深層次的機理和規律，可認為這是制約競技羽毛球運動發展的極為重要的原因之一。

2 結果與分析

美國《哈珀柯林斯社會學詞典》對理論的定義是：理論是“由邏輯的或數學的陳述所連接的一組假設或命題，它對經驗現實的某一領域或某一類現象提出解釋”；理論是“以一種系統化的方式將經驗世界中某些被挑選的方面概念化并組織起來的一組內在相關的命題”。

2.1 高遠球與成績關系的研究

后場高遠球是由底線擊至對方底線的一種高弧線飛行球。

后場高遠球由于飛行弧線高，速度慢、到達對方底線所用時間較長，而且不易被對方攔截，因而它能迫使對方遠離“中心位置”退到底線擊球，在被動狀態下運用此技術可為自己爭取回位時間，以便過渡和調整擊球位置，調整場上的比賽節奏，從而擺脫被動局面。

如圖1所示，進攻隊員p在右后場區打一拍正手直線高遠球，防守隊員就要從中場跑動至左后場區去回擊高遠球，回擊的高遠球可以是回直線、也可以回中線、同時也可以回大對角，落點如DP1、DP2、DP3。從圖中可以看出，直線落點DP1、中線落點DP2、的跑動距離都在半場的范圍之內，進攻隊員可以做出很多的回球動作，并且回球質量也會很高，只有落點DP3的球在另一個場區，所以進攻隊員跑動的距離是最遠的，也是最被動的，回球質量也是最差的。此時落點DP3的球才有可能把被動的局勢扭轉。因此，我們假設：“在打高遠球時，將球擊到對手的反手位，高遠球的得分就越高”。

統計結果表明（表1）：（1）高遠球落點次數（t）方面，運動員在D2t落點的平均數0次之間，D1t和D3t落點的平均數5～9次之間，（t＝1.729，p＝0.144，p＞0.05），可認為差異無統計學意義；D1t和D2t、D2t-D3t處落點之間平均數差異明顯，且達到顯著性水平（D1t-D2t，t＝5.171，p＝0.004，p＜0.05；D2t-D3t，t＝7.201，p＝0.001，p＜0.05）。（2）高遠球偏度得分（S2）方面，由于根據我們的判斷，距離中場站位越遠、接球難度越大，因此，區域D2接球最易、區域D1和D3接球最難，表1中D1t和D3t數據呈現出明顯的趨勢特點，直接支持我們這個觀點。正是基于該觀點，不同區域賦權后，區域D1s2-D3s2（t＝-0.050，p＝0.962，p＜0.05）差異達不到顯著性水平；區域D1s2-D2s2之間（t＝5.171，p＝0.004，p＜0.05）；區域D2s2-D3s2（t＝-7.201，p＝0.001，p＜0.05）差異達到非常顯著性水平。

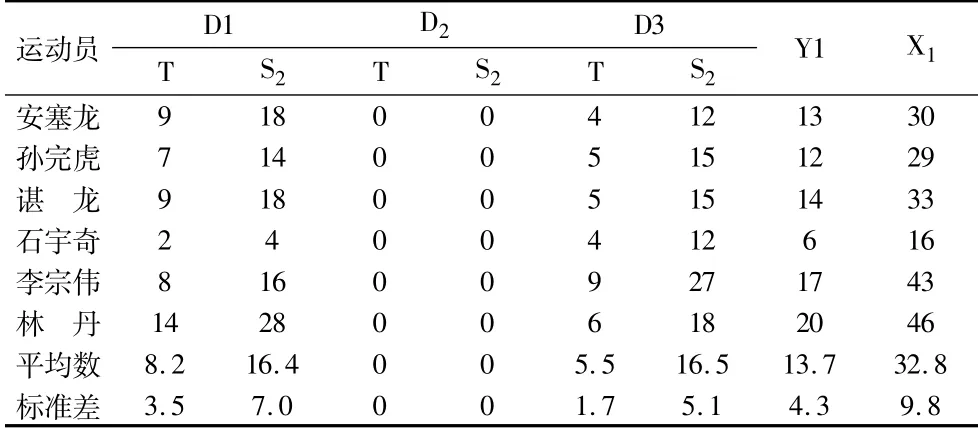
表1 運動員勾球落點及得分統計表

為了驗證Y1（三個區域落點總次數）與X1（三個區域總偏度得分）之間的關系，本研究采用皮爾遜相關系數的方法進行計算。為此，首先做出兩變量的散點圖，以判斷統計數據是否呈近似直線的關系，即檢驗本研究變量數據是否達到使用皮爾遜相關系數統計方法的要求。由散點圖（圖2）可知，高遠球得分與高遠球距離偏度總得分呈近似直線關系，因此，可采用皮爾遜相關系數r計算兩變量的相關系數。

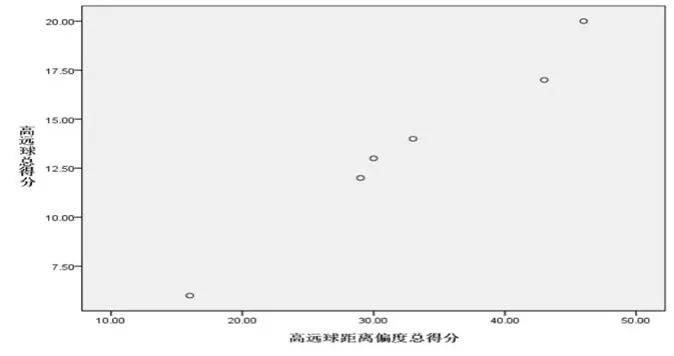
圖2 運動員偏度得分與得分散點圖

統計結果表明，Y1與X1之間達到高度相關（r＝.991**，p＜0.05），證實“在打高遠球時，將球擊到對手的反手位，高遠球的得分就越高”的假設。

2.2 吊球與成績關系的研究

后場吊球是將后場區域端線附近位置的球，回擊到對方前場區域（前發球線附近與球網之間）緊靠邊線兩角的近網小球。它可分為正手吊球和反手吊球兩種。

從圖3中可以看出，進攻隊員p可以在正手位右場區一個直線吊球落點為DP1，也可以斜線吊球落點為DP2，這兩個落點的球對于站在中場防守的隊員來說，距離基本是相等的。他回球的難易程度也差不多，但是對于進攻隊員來說，正（反）手的直線吊球的操作難度比斜線吊球的難度大。所以一般為了減少自己的主動失誤，保持主動的局面，在場上都會采用較容易操作又保險的技術動作。因此，我們假設：“后場吊球采用高手位主動吊球，擊球線路為斜線（落點為DP2），吊球的得分就越高”。

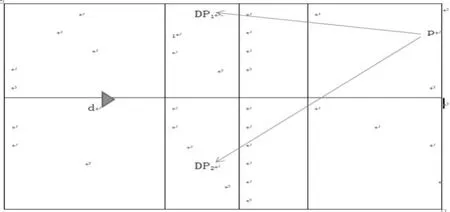
圖3 后場吊球的落點及防守隊員的站位示意圖

吊球落點次數（t）方面，運動員在D1t和D2t處落點的平均數8～10次之間，（t＝-0.672，p＝0.531，p＜0.05），可認為差異無統計學意義。這檢驗結果與我們的預期假設不一致，為了再次驗證數據，我們對接球區域難易程度進行賦值。

吊球偏度得分（S2）方面，由于根據我們的判斷，正（反）手的直線吊球的操作難度比斜線吊球的難度大，因此，區域D1吊球難度大、區域D2吊球容易，易得分。不同區域賦權后，區域D1s2-D2s2（t＝-3.433，p＝0.019，p＜0.05）；差異達到顯著性水平。

表2 運動員吊球落點及得分統計表

由散點圖（圖4）可知，吊球得分與吊球距離偏度總得分呈近似直線關系。因此，可采用皮爾遜相關系數r計算兩變量之間的相關系數。

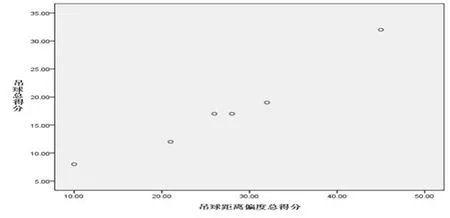
圖4 運動員偏度得分與得分散點圖

相關分析表明（表3），吊球落點距離偏度總得分與吊球得分相關系數r＝.975**（p＜0.05），表明吊球得分與吊球落點距離偏度總得分呈高度正相關關系，證實“后場吊球采用高手位主動吊球，擊球線路為斜線（落點為DP2），吊球的得分就越高”。

表3 吊球得分與吊球距離偏度總得分相關系數

2.3 殺球與成績關系的研究

后場殺球是針對對方擊至后場或中場區域的來球，爭取盡量高的擊球點，將球由高而下地想對方場區全力扣壓過去的一種球，采用高手位擊球。

從圖5中可以看出進攻隊員在正手位的一拍殺球可以有四種選擇，可以直線短殺落點為DP1，也已直線長殺落點為DP2，同時還可以選擇斜線短殺落點為DP4，還可以選擇斜線長殺落點為DP3。對于落點DP1和落點DP4的殺球，防守隊員上一步就可以將球救回，但是對于落點為DP2和DP3靠近邊線的長殺，防守隊員對于這種情況完全是屬于被動局勢。很有可能是直接失分的。所以在后場殺球中，靠近邊線的重長殺更有威力。因此，我們假設：“后場殺球越靠近邊線，落點越靠近底線的高手位重長，殺球的得分就越高”。

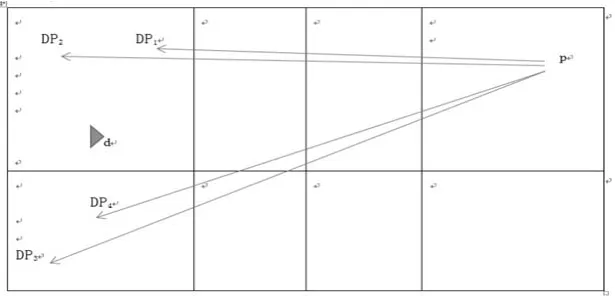
圖5 后場殺球的落點及防守隊員的站位示意圖

殺球落點次數（t）方面，運動員在D1t和D4t和D2t和D3t處落點的平均數8～38次之間，落點之間平均數差異明顯，且達到顯著性水平（t＝-23.606，p＝0.000，p＜0.05）。

殺球偏度得分（S2）方面，由于根據我們的判斷，距離中場站位越遠、接球難度越大，因此，區域D1接球最易、區域D3接球最難，表4中D3t數據呈現出明顯的趨勢特點，直接支持我們這個觀點。正是基于該觀點，不同區域賦權后，區域D1t和D4t和D2t和D3t（t＝-38.363，p＝0.000，p＜0.05）差異達到非常顯著性水平。

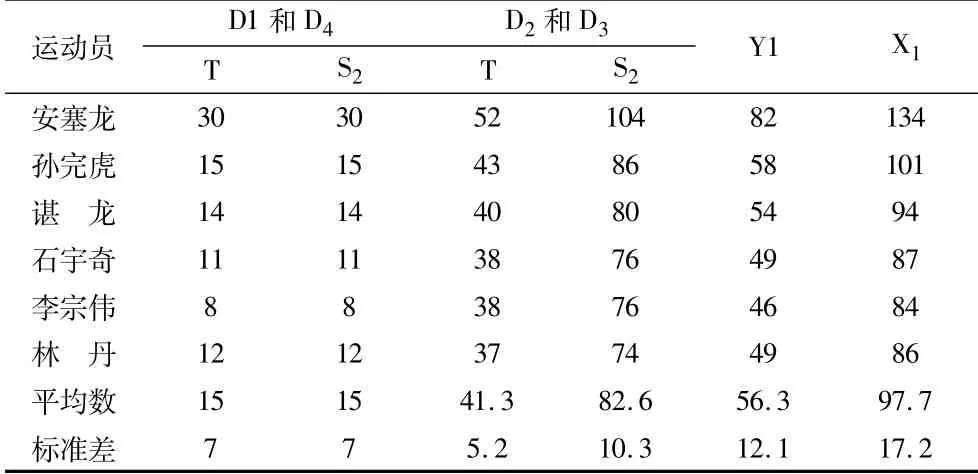
表4 運動員勾球落點及得分統計表

由散點圖（圖6）可知，殺球得分與殺球距離偏度總得分呈近似直線關系。因此，可采用皮爾遜相關系數r計算兩變量之間的相關系數。

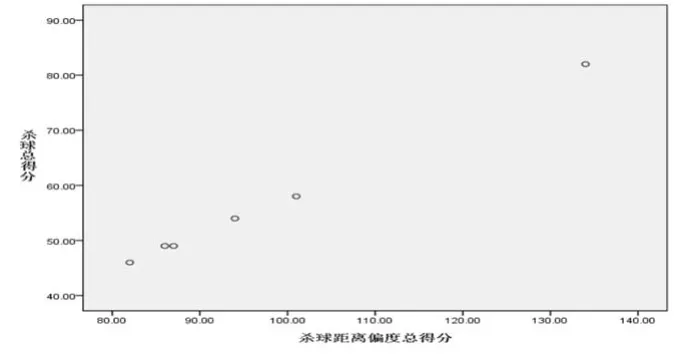
圖6 運動員偏度得分與得分散點圖

相關分析表明（表5），殺球落點距離偏度總得分與殺球得分相關系數r＝.999**（p＜0.05），表明殺球得分與殺球落點距離偏度總得分呈高度正相關關系，證實“后場殺球越靠近邊線，落點越靠近底線的高手位重長，殺球的得分就越高”。

表5 殺球總得分與殺球距離偏度總得分相關系數

3 結論

3.1 在30場71局的比賽中，針對運動員后場技戰術行動進行分析，后場技術使用率從高到低依次是殺球、吊球、高遠球。但是其中高遠球屬于防守類型的技戰術，不是主要的得分手段。雖然不是主要的得分手段，但是只要高遠球技術過硬，依然影響著后場技戰術行動與成績之間的關系。

3.2 對世界優秀羽毛球男子后場單打技戰術行動與成績關系的觀察統計與皮爾遜相關系數計算分析，以及配對樣本T檢驗的統計方法進行驗證，證實了以下假設是成立的：

3.2.1 證實了“在打高遠球時，將球擊到對手的反手位，高遠球的得分就越高”。

3.2.2 證實了“后場吊球采用高手位主動吊球，擊球線路為斜線（落點為DP2），吊球的得分就越高”。

3.2.3 證實了“后場殺球越靠近邊線，落點越靠近底線的高手位重長，殺球的得分就越高”。