邊疆高校非數學專業學生數學素養調查
——以普洱學院為例

普粉麗，孫衛新，丁曉敏

1.普洱學院 數學與統計學院，云南 普洱 665000；2.普洱學院 發展規劃中心，云南 普洱 665000；3.普洱市思茅區第二小學，云南 普洱 665000

1 研究背景

在互聯網快速發展的今天，理解和應用數學已經成為人們日常生活和工作的需求。作為一名非數學專業大學生在將來的社會中分析與解決問題、進行各類計算、使用計算機等都離不開數學。2011 年頒布的《數學課程標準》指出，“數學素養”是現代社會每一個公民應該具備的基本素養[1]。2017 年頒布的《普通高中數學課程標準（2017 年版）》指出，數學學科核心素養是數學課程目標的集中體現，是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現，是在數學學習和應用過程中逐步形成和發展的[2]。數學素養既是數學教育改革的目標也是提高數學教育質量的關鍵。

2 數學素養的內涵界定

早在20 世紀80 年代，著名數學教育專家科克羅夫特（Wilfred Cockcroft）就提出“數學素養”是指個人在社會生活中所需要的數學，并能運用數學技能處理日常生活中的數學問題，懂得欣賞和理解用數學語言表達的信息（如圖表、曲線、百分比等）[3]。

1994 年張奠宙[4]認為，數學素養包括知識觀念、創造能力、思維品質、科學語言。2000 年顧沛[5]認為，數學素養是指抓住數學問題的背景和本質的素養；用準確、嚴格、簡練的數學語言表達數學思想的素養；具有良好的科學態度和創新精神，合理地提出數學猜想、數學概念；探尋解決問題的素養；數學模型的素養。2009 年康世剛[6]認為，學生的數學素養包含數學知識素養、數學應用素養、數學思想方法素養、數學思維素養與數學精神素養。2015 年何小亞[7]認為，數學素養包括數學運算、數學意識、數學推理、數學思想方法和數學情感態度價值觀。

3 調查對象

普洱學院地處祖國西南邊陲，位于大昆曼國際通道上的樞紐城市——普洱市。40 多年的辦學歷程，形成了自己的特色。因此，調查對象選取本校的物理教育專業、園林專業、生物教育專業等學生。

4 調查問卷與統計軟件

參考楊海艷的《數學專業大學生數學文化素養的調查研究》的問卷，改編本次的調查問卷。問卷設計共20 道目，編號為A1—A7 是對數學的認知考查，編號為B1—B3 是對數學應用意識的考查，編號為C1—C3 是對數學思想方法的考查，編號為D1—D4 是對數學美學價值的考查，編號為E1—E3 是對數學語言與交流的考查。每道題采用5 級量表，從“完全贊同”到“完全反對”分成5 個等級，對應得分從高到低依次記為5 分到1 分，也就是得分越高，說明學生的數學素養越好。共發放問卷169 份，回收且有效問卷為152 份，有效率為95%。本文應用統計軟件SPSS24.0 對非數學專業大學生的年級差異進行獨立樣本T 檢驗，根據統計結果進行分析。

5 調查結果與分析

5.1 數學知識素養

5.1.1 數學知識素養的調查

問卷調查中顯示，91%的學生認同“數學是研究現實世界中一切可能的量的關系的科學”的說法，僅有9%的學生持有反對態度，說明絕大多數學生認同數學是研究現實世界中一切可能的量的關系的科學。數學是大量的公式、定理和枯燥的計算，有30.9%的學生持反對態度，34.2%的學生保持中立態度，34.9%的學生持贊同。這說明學生對數學研究的對象認識還不夠明確，部分認識還存在片面性。

對“數學反映了人們積極進取的意志、細致周詳的推理、以及對于完美境界的追求”的認識中，僅有10.5%學生持反對態度。“數學問題的答案都是充分的，沒有答案的問題不能算數學問題”，有32.2%的學生認為反對，32.2%的學生基本反對，17.1%的學生持中立態度，18.4%的學生贊同。這說明大部分學生都知道數學問題并非都有答案。“數學可以鍛煉人們的邏輯思維能力”，有1.3%的學生完全反對，5.9%的學生基本反對，3.9%的學生持中立態度，88.9%的學生贊同。數學是思維的體操，絕大多數學生能認可這種說法，只有少部分學生不贊同。

5.1.2 數學知識素養的年級差異性分析

A1 的p 值為0.966 在于0.05，接受原假設，說明二、三年級的學生對數學是量的關系的科學認識無顯著性差異，二、三年級的均值相等。A2 的p 值為0.009 小于0.05，拒絕原假設，說明二、三年級的學生在對數學知識素養有顯著性差異，二年級的均值高于三年級的均值。A3 的p 值為0.025 小于0.05，拒絕原假設，說明二、三年級的學生對數學反映了人們積極進取的意志、細致周詳的推理、以及對于完美境界的追求有顯著性差異，三年級的均值低于二年級的均值。A4 的p 值為0.013 小于0.05，拒絕原假設，說明二、三年級的學生對數學問題的答案都是充分的，沒有答案的問題不以能算數學問題的認識存在顯著性差異，二年級的均值高于三年級的均值。A5 的p 值為0.232 在于0.05，接受原假設，說明二、三年級的學生對數學可以鍛煉人們的邏輯思維能力的認識無顯著性差異，三年級的均值高于二年級的均值。A6 的p 值為0.047 小于0.05，拒絕原假設，說明二、三年級的學生對數學的抽象思維能力的認識存在顯著性差異，三年級的均值高于二年級的均值。

非數學專業的學生到二、三年級時，有的專業可能會繼續學習相關數學課程。這表明二、三年級學生的數學知識素養水平相差不大。

5.2 數學應用意識素養

5.2.1 數學應用意識素養的調查

“數學與人們的社會實踐活動密切相關”，2%的學生完全反對，7.2%的學生基本反對，17.8%的學生持中立態度，40.1%的學生基本贊同，32.9%的學生完全贊同。“數學在自然科學和社會科學中都有著廣泛的應用”中，3.9%的學生完全反對，3.3%的學生基本反對，13.8%的學生持中立態度，36.1%的學生基本贊同，42.1%的學生完全贊同。“估算、記錄、做決定都是數學的應用”，有6.6%的學生反對，27%的學生持中立態度，66.4%的學生持贊同意見。這說明絕大多數學生能正確理解數學應用的特點，只有少數學生對數學應用的認識水平不高。

5.2.2 數學應用意識素養的年級差異性分析

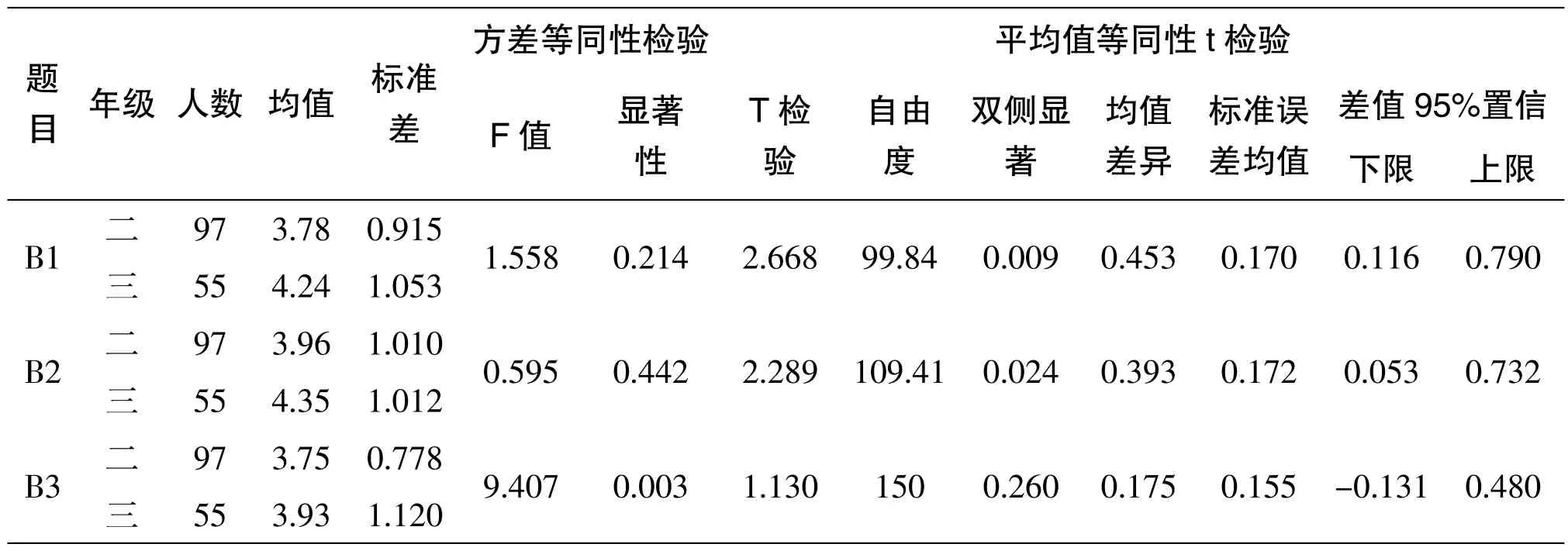
表2 數學應用意識的年級差異

B1 的p 值為0.009 小于0.05，拒絕原假設，說明二、三年級的學生在數學與人們的社會實踐活動密切相關的認識中有顯著性差異，三年級的均值高于二年級的均值。B2 的p 值為0.024 小于0.05，拒絕原假設，說明二、三年級的學生在數學在自然科學和社會科學中都有著廣泛的應用的認識中有顯著性差異，三年級的均值高于二年級的均值。B3 的p 值為0.260 大于0.05，接受原假設，說明二、三年級的學生對數學的應用的認識中無顯著性差異，但三年級的均值也略高于二年級的均值，說明三年級學生的數學應用意識素養比二年級的學生好。

5.3 數思想方法素養

5.3.1 數學思想方法素養的調查

“數學的發展主要靠嚴密的演繹推理，與人們的實踐活動和歸納法聯系不強”中有63.8%的學生反對，有19.7%的學生贊同這一說法。“極限斷想是整個數學中最根本最重要的數學思想之一”有僅有8.6%的學生持反對意見；“掌握數學的精神、思想和方法對于一個人在未來工作中解決問題有重要意義”中僅有8.5%的數學持反對態度，66.5%的學生持贊同意見，25%的學生持中立態度，這說明學生對數學精神、思想和方法對一個人未來的生活影響至深。

5.3.2 數學思想方法素養的年級差異性分析

C1 的p 值為0.000 小于0.05，拒絕原假設，說明二、三年級的學生在數學的發展主要靠嚴密的演繹推理，與人們的實踐活動和歸納法聯系不強的認識中有顯著性差異，三年級的均值小于二年級的均值。C2 的p 值為0.095 大于0.05，接受原假設，說明二、三年級的學生在極限斷想是整個數學中最重要的數學思想的認識中無顯著性差異，三年級的均值高于二年級的均值。C3 的p 值為0.077 大于0.05，接受原假設，說明二、三年級的學生在掌握數學的精神、思想和方法對于一個人在未來工作中解決問題有重要意義的認識中無顯著性差異，但三年級的均值也略高于二年級的均值。

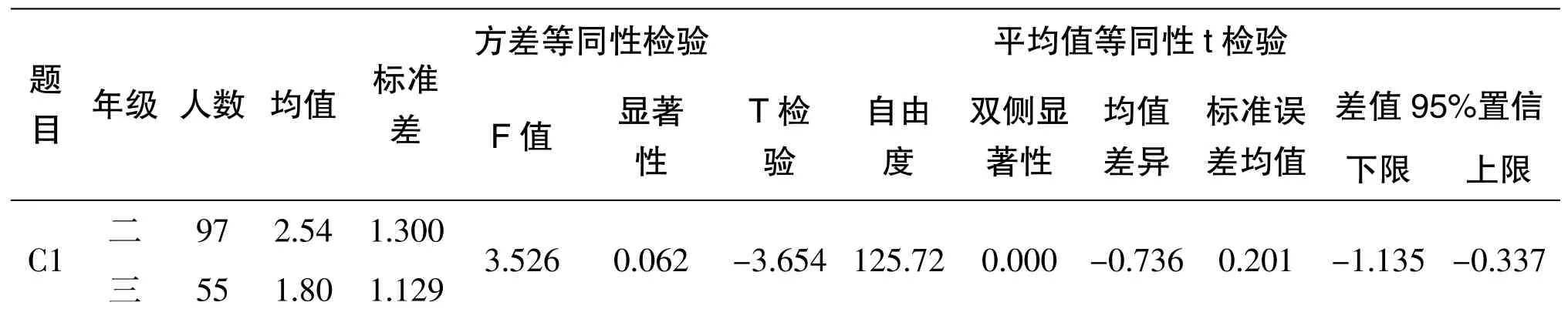
表3 數學的思想方法年級差異

5.4 數學美學素養

5.4.1 數學美學素養的調查

“數學有著和音樂或詩一樣的美”有6.6%的學生完全反對，3.9%的學生基本反對，28.9 的學生保持中立，26.3%的學生基本贊同，34.2%的學生贊同。“數學中高度的抽象性、邏輯的嚴密性和應用的廣泛性中也蘊含著極其豐富的審美因素”中僅有2%的學生完全反對，3.9%的學生基本反對，25%的學生持中立態度，30.3%的學生基本贊同，38.8%的學生完全贊同。這表明絕大多數非數學專業的學生除能體會到數學的特點之外也能認識到數學特點之中的美學價值，也有一小部分學生無法體現會數學特點中蘊含的美學價值。“數學具有簡單美、對稱美、統一美和奇異美”有1.3%的學生完全反對，8.6%的學生基本反對，21.1%的學生持中立態度，32.9%的學生基本贊同，36.2%的學生完全贊同。這說明69.1%的非數學專業學生對數學的美可以從不同的角度審視，數學的簡單美、對稱美、統一美和奇異美構成數學美的主體。“數學中對復雜的對象施以復雜的運算結果得到最簡單的數1，體現了數學是帶有神秘色彩的藝術品”有3.3%的學生完全反對，5.9%的學生基本反對，28.3%的學生持中立態度，30.9%的學生基本贊同，31.6%的學生完全贊同。這說明絕大多數學生能感受到數學的簡潔美。

5.4.2 數學美學素養的年級差異性分析

D1 的p 值為0.001 小于0.05，拒絕原假設，說明二、三年級的學生在數學中高度的抽象性、邏輯的嚴密性和應用的廣泛性中也蘊含著極其豐富的審美因素的認識中有顯著性差異，三年級的均值高于二年級的均值。D2 的p 值為0.000 小于0.05，拒絕原假設，說明二、三年級的學生在數學具有簡單美、對稱美、統一美和奇異美的認識中有顯著性差異，三年級的均值高于二年級的均值。D3 的p 值為0.075 大于0.05，接受原假設，說明二、三年級的學生在數學中對復雜的對象施以復雜的運算結果得到最簡單的數1，體現了數學是帶有神秘色彩的藝術品的認識中無顯著性差異，但三年級的均值也略高于二年級的均值。

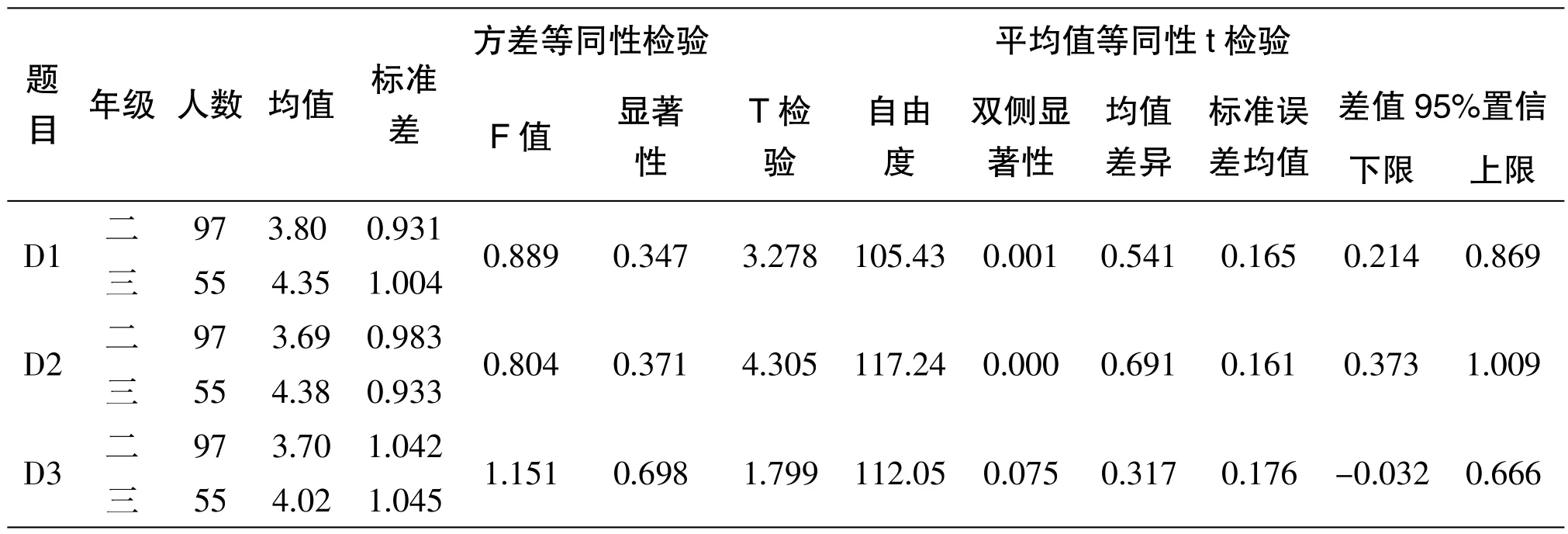
表4 數學美學素養的年級差異

5.5 數學語言與交流素養

5.5.1 數學語言與交流素養的調查

“數學語言是表達和交流的一種重要工具”有3.3%的學生完全反對，12.5%的學生基本反對，25.7%的學生持中立態度，40.8%的學生基本贊同，17.8%的學生完全贊同，將近五分之一的學生并不認同數學語言是表達與交流的一種重要工具。“十進位制計數法是人類最美妙的文明之一”中3.9%的學生反對，34.2%的學生持中立態度，61.9%學生持贊同意見。由此可知，非數學專業學生對數學語言的理解有了一定的認識，但也有少部分學生對數學語言的理解還不夠深入。因此，加強數學語言的教學是提升每個人的數學素養途徑之一。

5.5.2 數學語言與交流素養年級差異性分析

E1 的p 值為0.045 小于0.05，拒絕原假設，說明二、三年級的學生在數學語言是表達和交流的一種重要工具的認識中有顯著性差異，三年級的均值略高于二年級的均值。E2 的p 值為0.004 小于0.05，拒絕原假設，說明二、三年級的學生在數學符號語言對數學的發展有重要的意義的認識中有顯著性差異。三年級的均值高于二年級的均值，兩個年級的均值都在4 分以上，且三年年級的分數達到4.45 分。E3 的p 值為0.013 小于0.05，拒絕原假設，說明二、三年級學生在十進位制計數法的認識中有顯著性差異，三年級的均值高于二年級的均值。

表5 數學語言與交流素養的年級差異性分析

6 提高非數學專業學生數學素養的策略

6.1 注重數學的精神、思想和方法的有效滲透

能否能從數學角度出發，用數學思想方法去分析問題、解決問題，是判斷一個人是否具有一定的數學素養。匈牙利著名的數學家羅莎彼德曾有一個生動的比喻：假如在一群科學家面前有煤氣灶、水龍頭、水壺和火柴，要想燒開水，應當怎么做？這可以鍛煉學生處理復雜的實際問題時，自覺地從數學角度出度、用數學的思想方法觀察和思考問題，并努力培養學生尋求數學解決問題的辦法。

6.2 滲透數學文化知識的教學

能否感知與欣賞美，反映出一個人的素養、情操、品位、境界的高低與否。數學美是數學問題的結論或解決過程適應人類的心理需要而產生的一種滿足感。因此，數學有結論之美、方法之美、結構之美，數學之美，美在純潔，美在和諧，美在對稱，美在奇異。因此，教學中融入數學文化知識，培養一定的數學審美情趣，提高審美能力，在美的熏陶下啟迪思維，陶冶情操，提升口味，促進學生的數學知識素養與數學美學素養。

6.3 整合數學與其他學科，增強數學應用意識素養

數學是一種工具，一種思維的工具，一種解決數學問題與實際問題的工具。教師教學時，可將社會活動或有社會背景的問題引入到課堂教學時，將有助于發展學生的數學素養。強調學生在理解基本概念的基礎上，能應用相關的數學知識來識別、處理和解決這些問題。可加大數學建模和數學在其他學科領域的應用，使學生體會到數學在各行各業的廣泛應用意識，激發和培養學生主動運用數學知識的意識與能力，提高大學生的數學素養。

6.4 注重數學語言與交流的教學

數學語言是一切科學的共同語言。比如波動理論靠傅立葉分析來說明，經濟學家用數學語言表述經濟運行規律；量子力學要通過理論來描述；生物學中的遺傳基因DNA 原來是數學中的雙螺旋線；物理中的布朗運動成為概率論中的語言；天文學的語言是微積分等。數學課程教學時，鼓勵學生學會數學思維、數學表達，從而提升學生的數學素養。

6.5 改變教學方法，增加數學文化素養

“教學有法，教無定法，貴在得法”，在課堂教學中選擇合適的教學方法，利用現代教育技術手段與網絡教學平臺進行教學。借助學習通、學銀在線、MOOC 及雨課堂網絡教學平臺中的數學文化、數學史與數學教育、大學數學等，為學生提供教學視頻，方便學生學習，從而增加學生的數學文化素養。