永磁同步電機分數階改進快速終端滑模控制

王興亮，秦露露，顧 華，陳 依，曹基南，陸敏安

（1.國網上海市電力公司青浦供電公司，上海 201799；2.國網上海市電力公司松江供電公司，上海 201600）

現階段，在汽車、有軌電車和電力傳動系統等許多領域都廣泛應用了永磁同步電機PMSM（permanent magnet synchronous motor），其具有結構簡單、效率高、損耗小、動態性能好等優點[1]，但由于自身電磁特性，使得PMSM存在非線性性、外部抗干擾能力弱、參數不確定等缺點，PID控制方法無法達到所期待的控制要求。

國內外學者相繼提出了一些控制方法，包括自適應控制[2]、狀態反饋控制[3]、預測控制[4-5]和滑模控制SMC（sliding mode control）[6-9]等來提高PMSM的控制性能，其中SMC因對外界擾動和系統參數變化具有很強的魯棒性而得到廣泛的應用[10-11]。文獻[6]提出了改進滑模極值搜索控制算法，即在無穩態振蕩情況下，無需載波就可以直接產生開關信號的功率滑模控制器來改善系統的跟隨性，避免了傳統的風能轉換系統PI控制器中參數調整的過程。文獻[7]利用積分滑模控制ISMC（integral SMC）方法來控制PMSM，在傳統滑模面中加入了積分項，消除了穩態誤差，證明了SMC比PI控制在系統穩定性和抗擾動性方面具有優越性。文獻[8-9]采用基于精確反饋線性化的非奇異終端滑模控制NTSMC（nonsingular terminal sliding-mode control）方法控制永磁同步電機，在傳統SMC的基礎上提升了控制性能，保證了系統的有限時間穩定性。另外，相關學者針雙級矩陣變換器TSMC（two-stage matrix converter）可能存在的收斂速度慢的缺點，提出了快速終端滑模控制FTSMC（fast terminal SMC）[12-14]。

上述文獻研究的SMC都是整數階控制，隨著分數階微積分理論的完善和系統控制性能要求的提高，分數階控制被不斷研究并廣泛應用于各類線性和非線性系統中[15]，包括分數階PI即FOPI（fractional-order PI）控制、分數階自適應控制、分數階最優控制和分數階滑模控制FOSMC（fractional-order SMC）等[16]。傳統控制器微分、積分階次都可以設置成不同整數，分數階控制器的微分、積分階次可以為任意實數，這使得其在參數調節上具有更大的靈活性，能夠提高系統的控制性能[17]。近年來，FOSMC也被研究并應用于PMSM控制中。文獻[18]將傳統滑模趨近律中的符號函數用分數階次的符號函數取代，提高了趨近速度，抑制了系統抖動，但其并不是在滑模面中直接引入分數階微積分。文獻[19]將傳統滑模面的微分項改進為分數階次微分項，提高了系統的綜合控制性能。文獻[20]提出分數階ISMC方法，證明了該控制方法對定子電阻和電感的不確定性具有較強的魯棒性。

本文以FTSMC為基礎，提出一種分數階改進快速終端滑模控制FOIFTSMC（fractional-order improved FTSMC）方法。在PMSM速度環上采用可以實現系統的有限時間控制和快速收斂的FOIFTSMC，電流環上應用FOPI控制器。同時，針對外部負載擾動和系統參數不確定的問題，設計了1個分數階擾動觀測器FODOB（fractional-order disturbance observer），將擾動觀測值反饋給滑模控制器。本文所提出的控制方法通過Lyapunov定理證明是穩定的[21]，而頻域分析主要用來證明系統的穩定性區域，因此本文僅進行時域分析就能檢驗控制方法的改進效果。仿真結果表明FOIFTSMC方法具有更好的動態響應性能和抗擾動性能。

1 PMSM數學模型

PMSM在dq軸參考坐標下的狀態方程[22]為

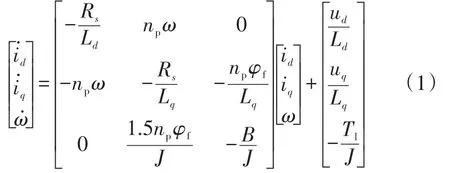
式中：ud、uq分別為d、q軸定子電壓；id、iq分別為d、q軸定子電流；Ld、Lq分別為d、q軸定子電感，Ld=Lq；Rs為定子電阻；ω為電機轉子機械角速度；np為電機極對數；φf為轉子磁勢；Tl為負載轉矩；B為黏性摩擦系數；J為轉動慣量。

從式（1）可以看出，PMSM的交軸和直軸電流存在耦合關系，不能獨立調節。在實際控制過程中，通常將直軸參考電流設為0，來消除耦合關系。圖1為PMSM雙閉環控制結構，其中ω*為參考轉速。

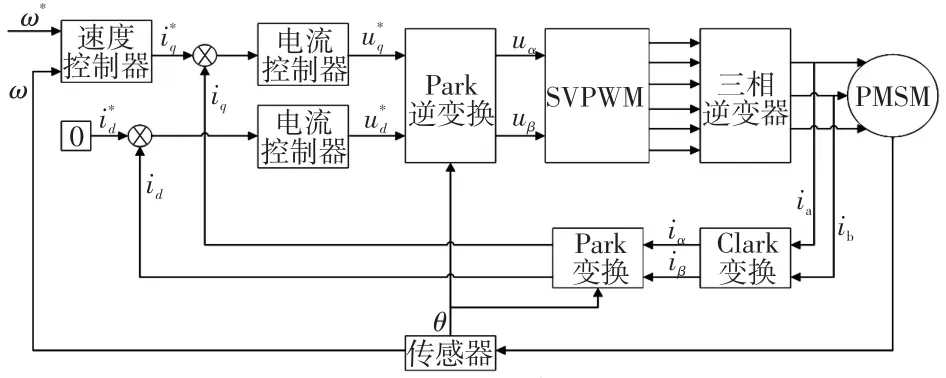
圖1 PMSM控制結構Fig.1 Control structure of PMSM

對于傳統的PMSM控制，一般在系統的電流環采用PI控制，速度環采用SMC方法[6-9]。本文將同時對兩個控制器進行改進，在電流環上采用FOPI控制，相比傳統的PI控制，FOPI多了1個可調的積分階數參數，能讓dq軸電流更好地跟蹤給定信號id*和iq*；在速度環上采用FOIFTSMC方法，在保證系統有限時間控制的基礎上，提升了系統的控制性能和抗擾動性能。

2 控制器設計

2.1 分數階微積分

分數階微積分是整數階微積分的擴展，相關分數階微積分的定義有很多，其中使用最廣泛的是Riemann-Liouville（RL）定義的分數階微積分。RL型分數階積分定義可表示為

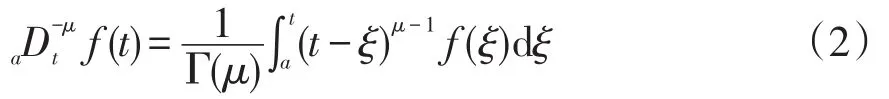
式中：t、a分別為積分上限、下限；μ為分數階積分階次，μ＞0；Γ（μ）為gamma函數。RL型分數階微分定義為

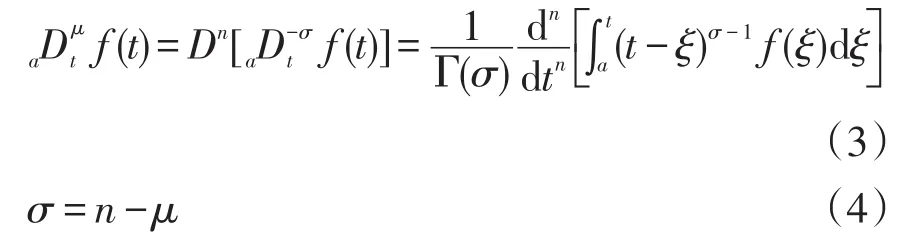
式中：σ為分數階積分階次的差值；n為大于μ的最小整數。

為了方便計算，分數階微積分通常在Laplace域中計算，其零初始條件下（輸入、輸出同時滿足在初始時刻之前各值及其導數均為0）的Laplace變化為

在工程應用中，分數階微積分傳遞函數可以用整數階傳遞函數來近似替代。本文仿真過程中使用Oustaloup算法來近似分數階傳遞函數，算法的具體計算過程在文獻[23]中有詳細介紹，剩余部分用Dμ來替代aDtμ。

2.2 電流環FOPI控制器設計

本文PMSM的電流環設計了FOPI控制器，其傳遞函數為

式中：kp、ki分別為比例增益、積分增益，kp＞0、ki＞0 ；λ為積分階次，λ∈[0，2]。當λ=1時，G（s）為傳統的PI控制。由圖1可知，iq可表示為

由式（1）可以得到iq和ω在Laplace域的關系式為

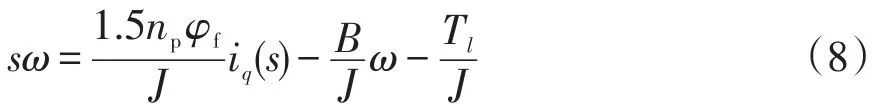
結合式（7）和式（8）可以得到系統分數階速度方程為

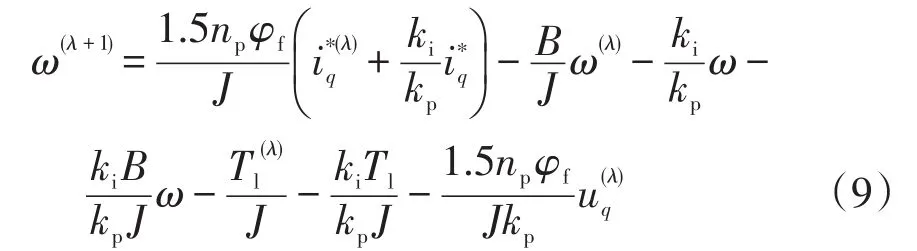
式中，ω(λ+1)為分數階電機機械角速度。

這里做如下定義：

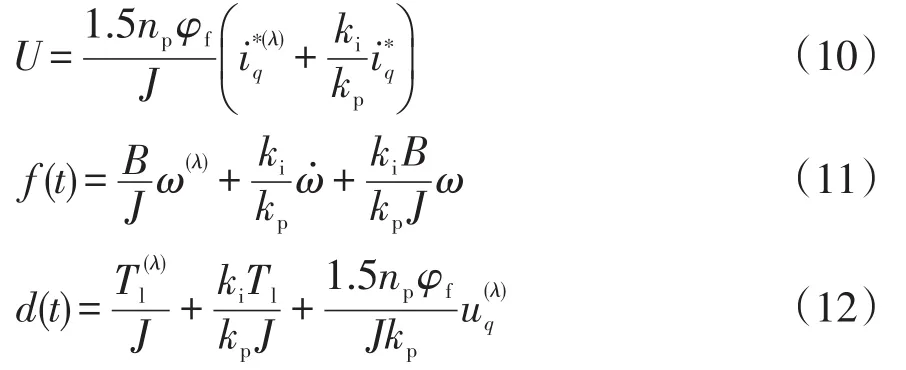
式中：φf為轉子磁勢；d（t）為系統參數不確定和外部擾動項。

式（9）可以簡化為

2.3 速度環FOIFTSMC控制器設計

本文PMSM的速度環設計了滑模控制器，滑模面設計為速度誤差(e=ω*-ω)的函數。根據式（13）可以得到如下的系統誤差方程：

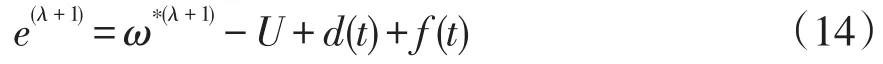
滑模控制器設計包含兩個步驟：①設計合適的滑模面；②設計合適的控制方法使系統能夠在有限時間內到達滑模面。為了實現系統有限時間控制，可以選用如下的終端滑模面：

然而，當系統狀態遠離平衡點時，TSMC的收斂速度較慢。為了提高系統的全局收斂速度，FTSMC和改進快速終端滑模控制IFTSMC（improved FTSMC）可分別表示為

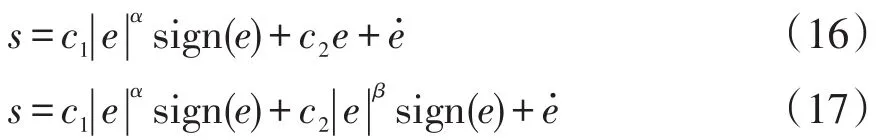
當誤差e遠離平衡點時，動態方程近似為，可以實現快速收斂；當誤差e接近平衡點時，動態方程近似為，可實現有限時間收斂[24]。

為了進一步提高系統的控制性能和魯棒性，本文將分數階微積分與IFTSMC相結合，提出了FOIFTSMC控制方法，其滑模面可表示為

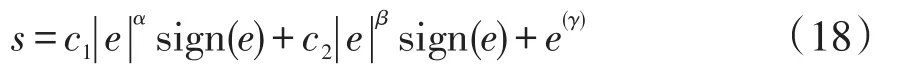
式（15）～（18）的滑模面中，c1、c2、α、β均為常數，c1＞0、c2＞0、0＜α＜1＜β＜2；γ為分數階微分階次，0＜γ＜1。式（18）的微分式為

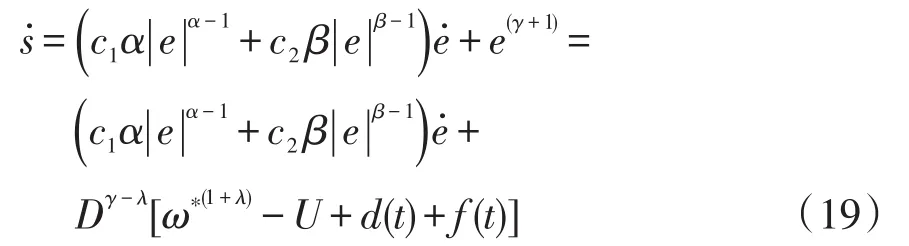
系統的控制律可由式（19）得到，即

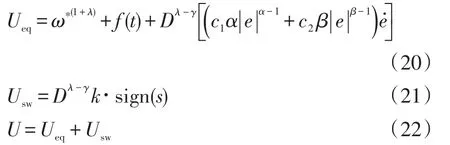
式中，k為切換增益，k＞0。

論點1若切換增益k滿足式（23），則當系統控制律如式（22）所示時，所設計的FOIFTSMC控制系統是Lyapunov穩定的，即

證明1定義1個Lyapunov能量函數為

結合式（19）和式（22）可得

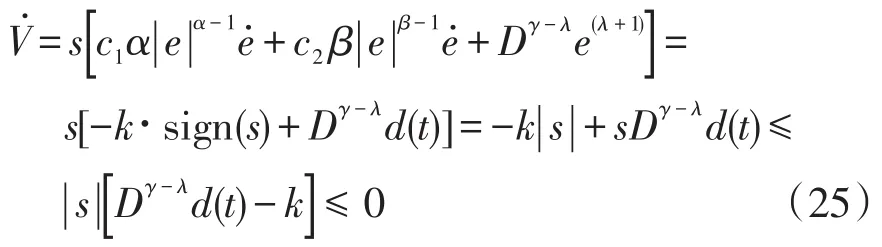
根據Lyapunov穩定性理論可知，所設計的基于FOIFTSMC+FOPI控制的PMSM是穩定的。

3 FODOB設計

第2節設計的FOIFTSMC+FOPI控制器只有當切換增益k滿足式（23）時，系統才能穩定。由于擾動項d（t）是不確定的，因此切換增益k必須設計得足夠大，但是k值過大會加重SMC的抖振現象。相關文獻研究設計了擾動觀測器來解決此問題。

由于本文PMSM所設計的FOIFTSMC+FOPI控制是1個分數階控制系統，所以傳統的擾動觀測器并不適用。本文參考文獻[25]提出的FODOB并設計應用在本文所提的控制系統中。1個分數階系統可表示為

式中：α為分數階次，0＜α＜1；(x1,x2,…,xn)T為系統狀態量；u為控制輸入；d為擾動量；（fx）、g（x）為已知函數。擾動d滿足

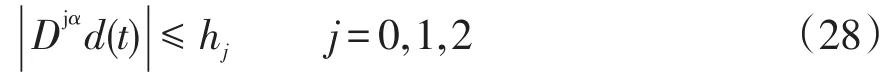
式中，hj為未知正實數。

FODOB可設計為

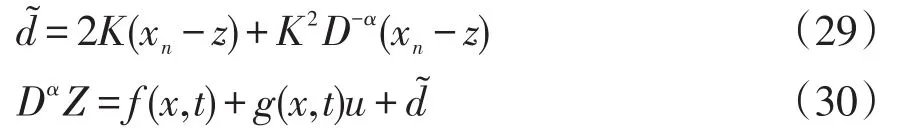
式中：K為待確定的正實數；z為輔助變量；為擾動觀測值。

系統速度誤差方程（14）可以修改為

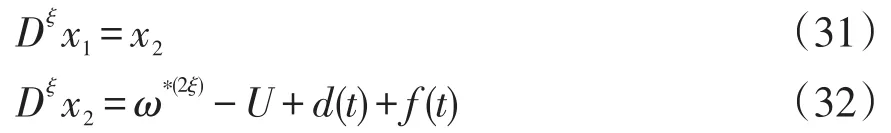
式中：ξ=(1+λ)/2；x1=e；x2=e(ξ)。FODOB可改寫為

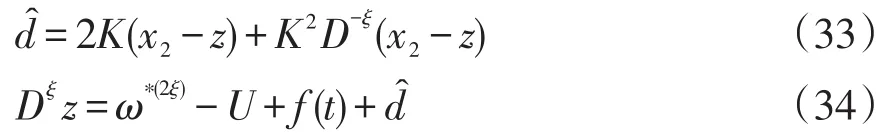
根據上述分析，控制律方程式（22）可以改為

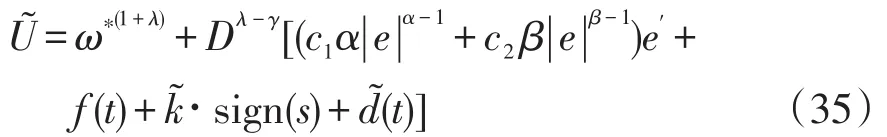
論點2若切換增益滿足式（36），則當系統控制律如式（35）所示時，所設計的FOIFTSMC+FODOB控制系統是Lyapunov穩定的，即

證明2定義Lyapunov能量函數仍為式（24），結合式（35）與式（19）可得

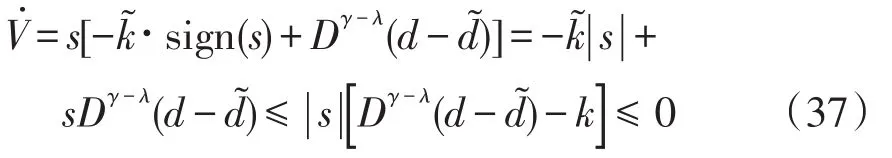
根據Lyapunov穩定性理論可知，所設計的基于FOIFTSMC+FOPI+FODOB的控制系統是穩定的。圖2為綜合分數階控制器下的PMSM控制系統。

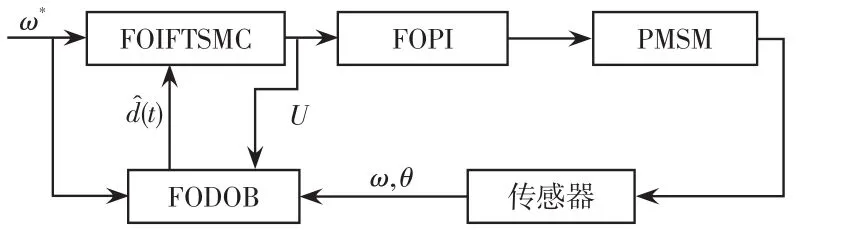
圖2 綜合分數階控制器下的PMSM控制系統Fig.2 PMSM control system with composite fractional-order controller

4 仿真結果

為了說明綜合分數階控制器的有效性，本文在Matlab/Simulink下對PMSM控制系統進行了仿真。仿真所用PMSM參數如表1所示。

表1 PMSM參數Tab.1 Parameters of PMSM

4.1 起動時系統特性

仿真中對 TSMC+PI、IFTSMC+PI、FOFTSMC+FOPI和FOIFTSMC+FOPI等4種控制方法進行對比分析。為了方便比較，各控制器參數選取基于以下原則：①4個控制方法的切換增益、比例增益、微分增益和α值相同；②參數c1與c2之和(c1+c2)相同；③IFTSMC與FOIFTSMC之間只有分數階微積分階次γ和λ不同；④FOFTSMC與IFOFTSMC的微積分階次γ和λ相同。

假設PMSM參考速度為700 r/min。圖3為系統起動時速度與電流iq對比曲線。從圖3可以得出如下結論：①啟動過程中，TSMC的收斂速度慢，IFTSMC能明顯提高收斂速度；②分數階統整數階控制系統，能夠更快地到達穩定狀態；③相比FOFTSMC，FOIFTSMC的速度超調量更小，電流波動也更小；④分數階控制存在系統起動電流較大的缺點。

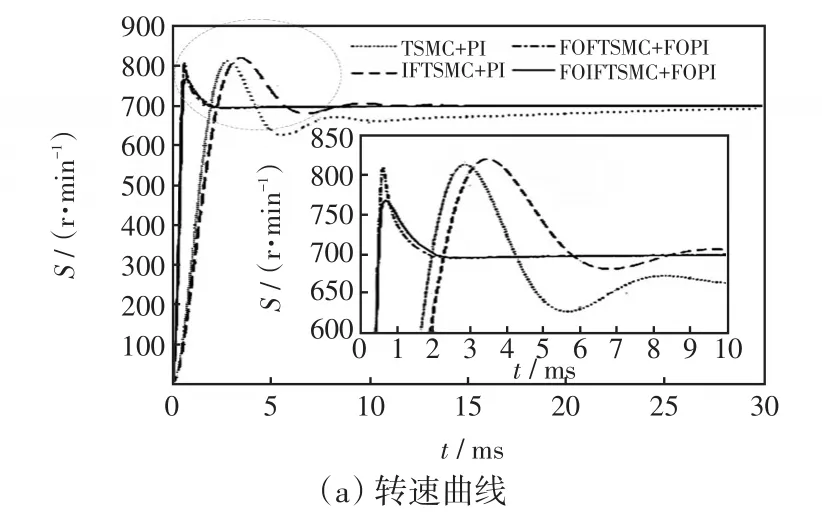
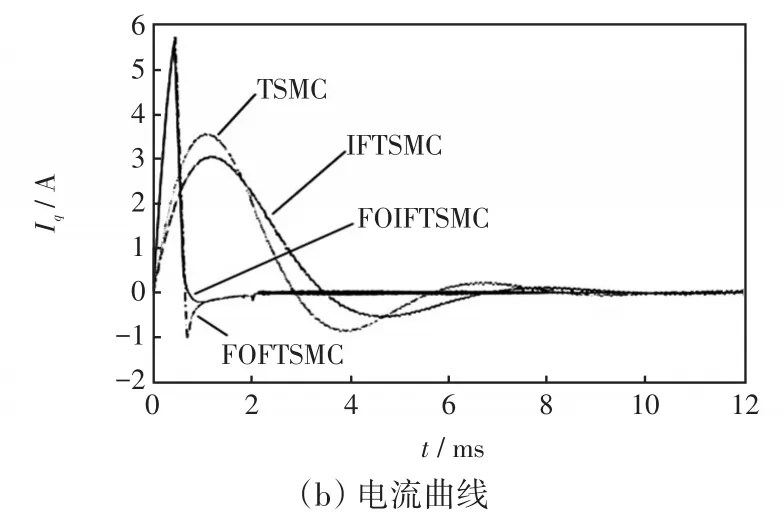
圖3 系統啟動時的速度電流響應曲線Fig.3 Response curves of speed and current when system starts

4.2 負載變動時系統特性

圖4和圖5分別為PMSM存在外界負載擾動時，IFTSMC和FOIFTSMC下速度與電流曲線對比。

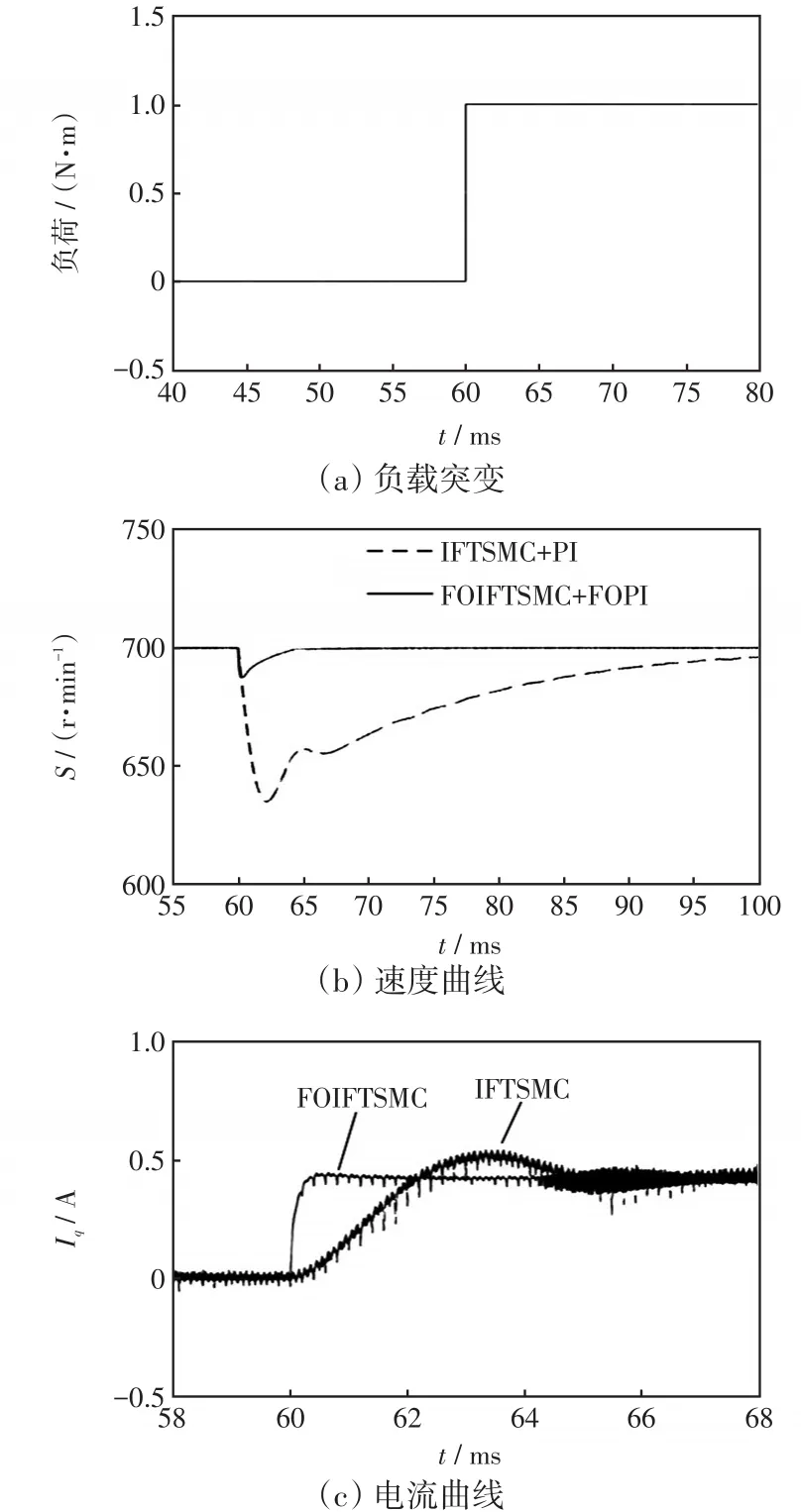
圖4 負荷突變時的速度、電流的響應曲線Fig.4 Response curves of speed and current when load changes suddenly

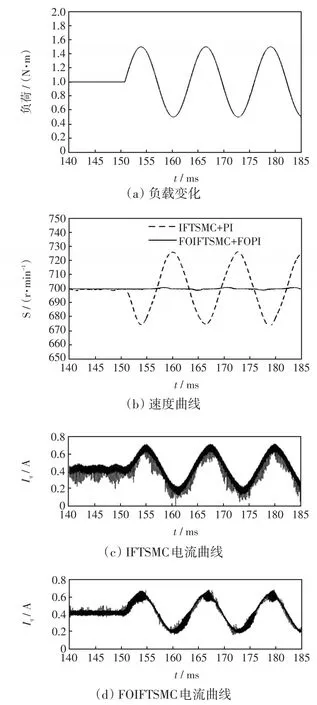
圖5 負荷持續變動時的速度電流響應曲線Fig.5 Response curves of speed and current when load changes continuously

從圖4可以看出，負載突變時，相比于IFTSMC，FOIFTSMC下系統速度突變量更小，能更快地恢復到參考值，電流調整到新穩態值的調整時間也更短。由圖5可知，當負載持續變動時，FOIFTSMC下系統速度的波動量被大大降低了，同時分數階滑模控制器能抑制電流的抖動問題。因此，將控制器從整數階改進到分數階能極大地增強系統的抗擾動性能。

第3節分析了擾動觀測器能進一步增強系統的抗干擾能力。為了說明所設計FODOB的有效性，圖6和圖7給出了PMSM在負載擾動時，FOIFTSMC加入FODOB控制下的速度、電流曲線。從圖6可知，當負載突變時，FODOB可以降低系統速度突變量，減少其恢復到參考值的時間，但是會引起1個瞬時大電流。從圖7可以看出，當負載持續變化時，FODOB能進一步降低系統速度波動上限、下限。

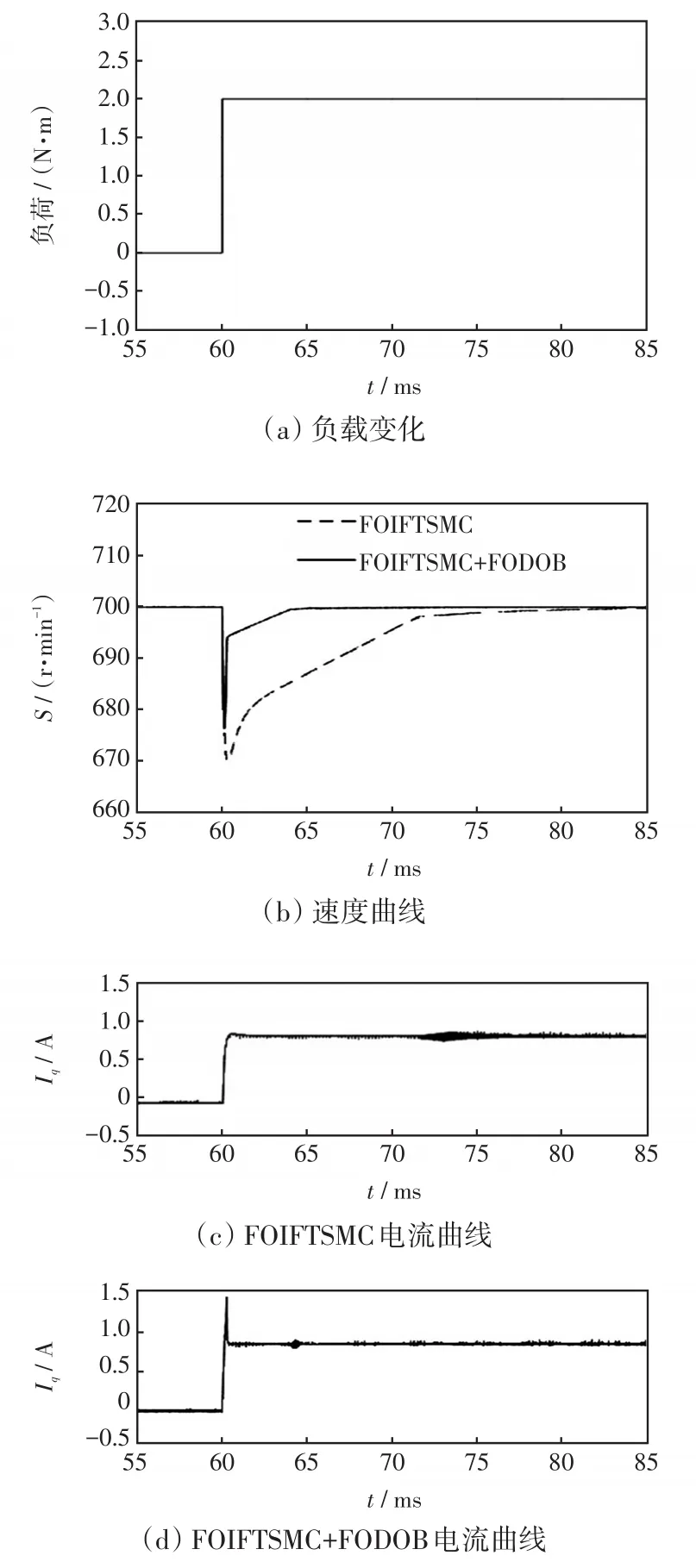
圖6 負荷突變時FODOB作用下的響應曲線Fig.6 Response curves with FODOB when load changes suddenly

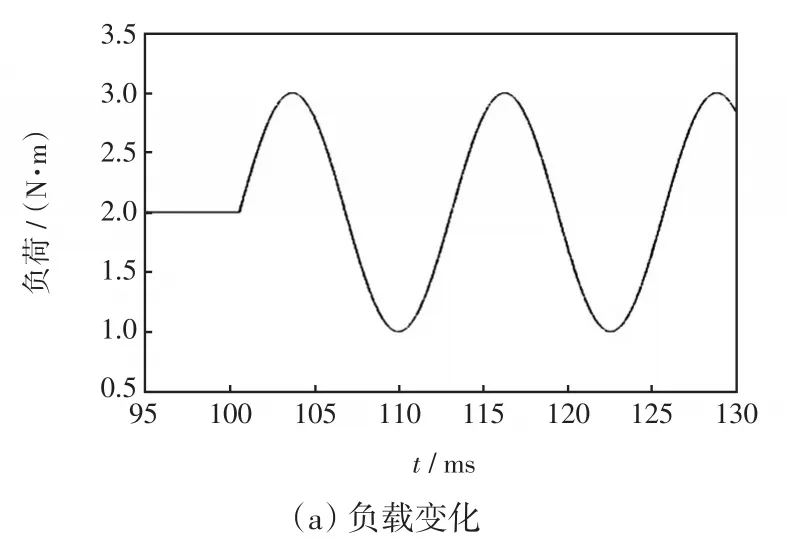
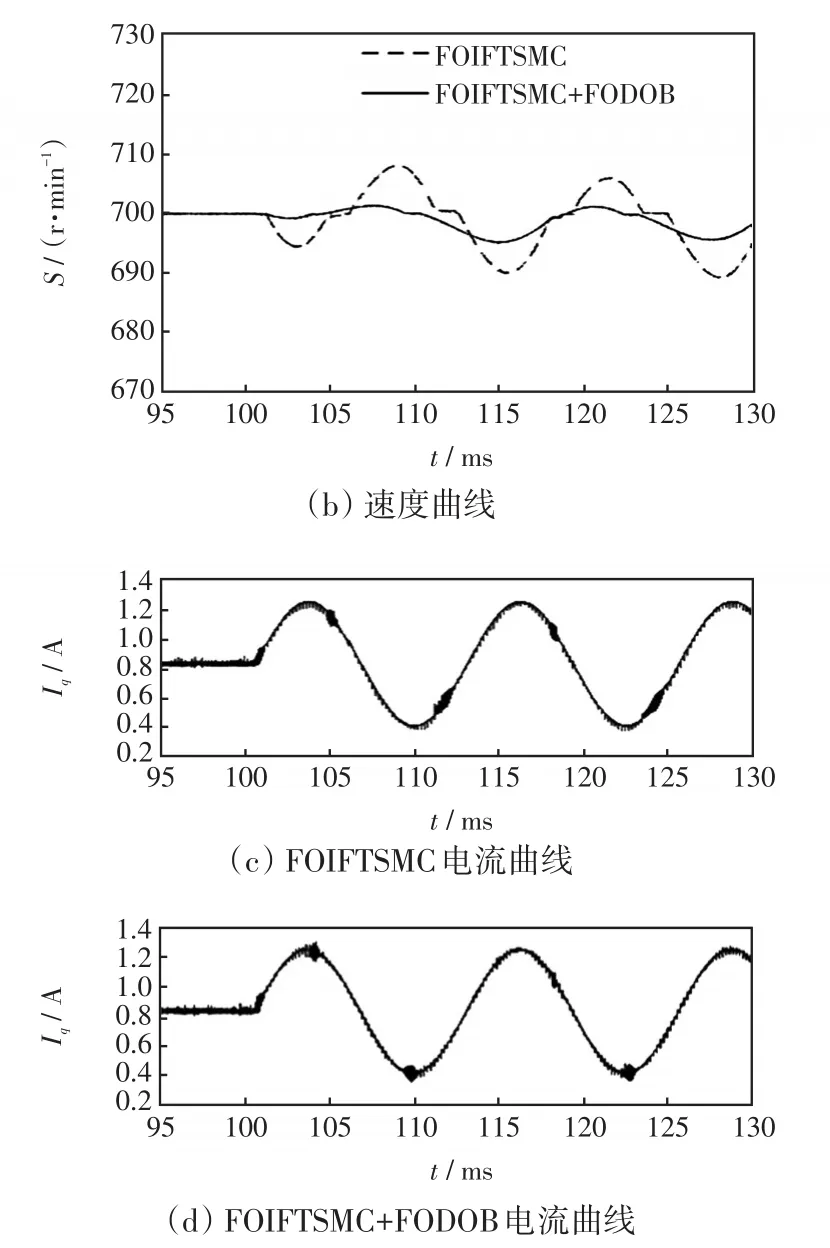
圖7 負荷持續變動時FODOB作用下的響應曲線Fig.7 Response curves with FODOB when load changes continuously

5 結語

本文將分數階微積分理論與SMC理論相結合，提出了一種FOIFTSMC方法來控制PMSM。此方法與PMSM中傳統SMC方法不同，在PMSM控制系統的電流環采用了FOPI控制，在速度環采用了本文所設計的FOIFTSMC方法。為了降低擾動對控制性能的影響，本文設計了1個分數階擾動觀測器。仿真實驗結果表明，相比整數階滑模控制，FOSMC方法能夠有效地提高系統的控制性能和抗擾動能力。同時，所設計的FODOB能進一步增強系統的抗擾動性能，減小了SMC的抖振問題。因此，本文方法適用在對PMSM調速性能要求高的系統上，但所設計的分數階控制方法存在起動電流偏大的缺點，這將是今后需要進一步研究的問題。