網絡環境下學生自主學習概率論能力的培養

曹曉春 荊文君 王艷梅

山西財經大學，山西 太原 030006

隨著信息化技術的發展，網絡、平板、手機等新型媒體深刻地改變著我們的學習和生活方式。高校學生作為受教育程度較高的主體，容易接受新事物、思想活躍，新型媒體對于他們來說已是飛入尋常“百姓家”。新型媒體尤其是網絡對傳統的教學產生了深刻的變革：以前是教師在課堂上占主導地位，學生被動地聽，兩者之間溝通和互動較少，而現在師生可以隨地在QQ、微信等上面快捷方便地交流和互動，老師能及時解決學生問題；學生還可以根據學科和自身需要隨時利用工具查閱學習信息，實現移動學習；網絡環境下的學習需要學生更加積極主動地參與，使得學生學習自主性有了更大的主觀能動性；網絡環境下的學習能給學生營造一種寬松自由的學習環境，能使得學生充分發揮他們的聰明才干；網絡環境下的學習使得學生不迷信老師，可以培養學生的獨立思考能力，使之能批判地、創造性地學習。如何有效利用網絡的便利性和靈活性，結合傳統教學模式，創立與時俱進的教學課堂，給教學方式改革帶來一股清風是我們研究的重點。

概率論與數理統計是一門應用性很強的學科，生活中很多實際問題都可以用概率論中的方法來分析和解決。如何使學生掌握基本概念、原理、思想和方法，對概率論與數理統計的整個知識體系有所了解，并將所學在實際問題中得以創新和運用，是數學教師在教學過程中需要不斷探索的問題。針對學生“學不致用”或“學難致用”問題，我們將利用網絡環境，結合此次新冠疫情，發動學生利用各種網絡環境收集相關數據，用概率論中的數學期望知識研究核酸檢測混采分組中的人數問題。除了讓學生順利完成課堂教學安排的基本內容外，還讓學生“學以致用”，能夠舉一反三，提高網絡環境下學生自主學習概率論的能力。下面我們將具體闡述這一過程在課堂上如何實施。

首先學習數學期望的概念。數學期望是隨機變量的數字特征之一，刻畫了隨機變量總體取值的平均水平。離散型隨機變量數學期望的定義如下：

定義［1］：設離散型隨機變量X的分布律為，若級數絕對收斂，則稱的值為離散型隨機變量X的數學期望，記作（E）X，即。

結合課本完成課堂教學安排的基本內容后，讓學生在國家衛生健康委員會網站、武漢市衛生健康委員會網站、世界衛生組織網站等網絡上了解新型冠狀病毒肺炎疫情的波及范圍、危害、診斷、預防、治療、疫苗等相關信息，獲取各地區確診病例、人口、核酸檢測等關鍵數據，為解決目標問題做好鋪墊。

一、問題提出

自2019年12月末以來，新冠疫情在全球已具有大流行特征，傳染速度快、傳播廣、變種多、致死率高，對社會生產和人民生活帶來巨大影響。根據世界衛生組織報道，截至2021年11月2日，新型冠狀病毒肺炎國外累計報告確診病例247755167例，造成累計死亡病例5015641例；國內累計報告確診病例126163例，累計死亡病例5696例［2］。為有效遏制疫情，核酸檢測是病患預防檢測及確診檢測的重要技術之一。核酸檢測方法有單采和混采兩種。單采就是一個人的采集拭子放到一個采集管中。混采是將若干個人的采集拭子放到一個采集管中，檢測結果為陰性時，混采樣本均視為陰性，代表混采的所有人都是安全的；如果出現陽性，相關部門會立即對該混采管的受試者暫時單獨隔離，并重新采集單管拭子進行復核，再確定這當中到底哪一個是陽性。混采最常用的包括5合1混采和10合1混采2種。一般情況下，對于發熱門診有癥狀患者、密切接觸者、重點區域人群等高風險人群檢測，建議采用單采單檢。在陽性率極低（0.1%）的情況下或進行大面積篩查則可以進行混采。而對于目前，對大面積篩查采用的是10合1混采。混采大幅提升了核酸檢測能力，可使日檢測能力在不增加人力物力的情況下，效率增加10倍，起到多篩查、減少傳播、節約社會成本的作用，提升了新冠病毒核酸檢測能力和效率，有效滿足了疫情常態化防控需求。

那么，為什么是10合1混采？15合1的混采可以嗎？究竟幾合1的混采在理論上是最經濟、高效的？檢測機構在決定10合1混采時，是通過理論計算還是根據實踐操作？在目前陽性率極低的情況下，可不可以把混采人數增多？根據這些提問，激發學生對新事物的探究熱情，引導學生自主探索，有效地啟發學生的思考，使學生成為學習的主體，為解決問題做好熱身準備。

二、數學期望在核酸檢測混檢分組人數問題中的應用

為使研究的問題具有一般性，假定n和1的混采是有效合理的。設每組核酸檢測的次數為隨機變量X，若混采采樣為陰性，則X=1若混采采樣為陽性，則CR武漢市截至2020年4月8日解封時，累計病例為50008例［3］，按留在城里900萬人口計算，個體被感染的概率為50008/900萬=0.5556%，從而得到隨機變量X的分布律

X 1 n+1 P （1-0.5556%）n 1-（1-0.5556%）n

按照離散型隨機變量數學期望的定義可知，每組平均檢測次數為

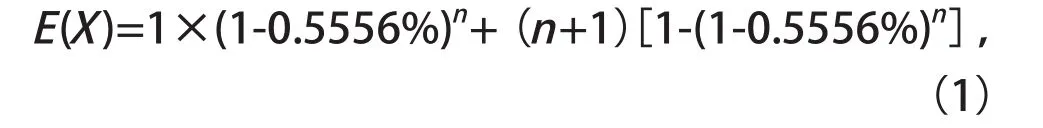
則全市900萬人平均檢測次數為：全市的分組數乘以每組平均檢測次數，即

要使檢測效率高，花費時間短，經濟成本低，就是要算當每組人數n為何值時，f（n）取最小值。

通過（1）（2）式解析式的建立，學生不僅掌握了當堂課的內容，還應用所學來解決國民經濟中遇到的問題，培養了分析問題解決問題的能力，鍛煉了采集數據、分析數據、處理數據的技能，進一步激發學習興趣，增強學習概率論與數理統計課程的信心。

要想求出（2）式中f（n）的最小值，學生們討論后發現用代數的方法在理論上是可行的，但是對于實際問題來說，不能得到理想的結果，研究后決定借助Matlab或Excel軟件處理大量數據的運算。概率論與數理統計課程有很多圖像和大量數據運算，學生可利用Matlab軟件繪制圖形，通過數形結合來加深對知識點的理解；借助于Excel、SPSS等辦公或統計軟件處理大量數據的運算，將學生從繁瑣的數字運算中解放出來，把更多的時間放在對概念和思想方法的正確理解上。通過本課程的學習，讓學生掌握一些基本的統計軟件，也是我們的培養目標之一。最后，學生借助Excel軟件，采用枚舉法算出全市平均檢測次數f（n），并制表1如下：

從表1可以看出，每組中隨著人數的增加，全市平均核酸檢測次數呈遞減趨勢，當n=14時達到最小值，隨后又呈遞增狀態，也就是說，在個體被感染概率為0.5556%的前提下，核酸檢測每組14人可以使全市平均檢測次數最少、花費最少、效率最高。由此學生們可以得出結論：不一定非得是10合1的混檢模式，14合1的混檢模式在理論上是更有效的。又注意到，（2）式中用到的個體被感染的概率為0.5556%。實際上，個體感染率應該小于0.5556%，因為在計算個體感染概率的時候，是用50008除以900萬，其中50008是武漢市從疫情以來到城市解封這一時間段內的累計確診病例，且患者一旦確診就被隔離，所以真正同時存在于社交網絡的染病者一定會遠遠小于50008，也就是說，0.5556%應該是高估了感染率，在此情況下，混檢采樣每組中的人數應該比理論算出的值14還要大。

表1 武漢市平均檢測次數（陽性率為0.5556%）

人們工作和生活中遇到的問題可能會有不止一種答案，但是如果不懂問題的來龍去脈和答案的確切含義，多種答案只能是學生的負擔。缺乏批判性思維、創新性的學生，就會被浩如煙海般的知識所淹沒。通過對核酸混檢幾合一問題的討論，培養學生用批判的眼光看待遇到的一切問題，從普遍認為是真理、定論、不可更改的事實中找出不合理的因素，用理性、科學的思維和方法對待周圍一切事物。

三、舉一反三

進一步啟發學生，如果個體被感染的概率較低，如從武漢市5月11日—5月21日對900萬人的核酸檢測結果知，陽性率僅為0.018%［3］，面對如此低的陽性率，10合1的混采檢測需要改進嗎？如果要改進，那么幾合1的混采模式是更合理有效的？需要學生進一步利用網絡搜集數據解決這類實際問題。與表1類同，學生們利用Excel，用枚舉法羅列出了5月11日—5月21日武漢市理論上的平均檢測次數f（n）。

從表2可以看出隨著每組混采人數的增加，在陽性率僅為0.018%的前提下，全市平均檢測次數逐漸減少，直到n=75時減到最低，隨后又逐漸增加，因此從數學理論上講，混采人數每組75人時，可以使全市平均檢測次數最少。

表2 武漢市平均檢測次數（陽性率為0.018%）

根據其他國家的新冠疫情，核酸檢測又該幾合1比較合理呢？鼓勵學生在網絡上搜集數據解決相關問題，加深對數學期望的理解，能舉一反三解決實際問題。

四、總結

在教學活動中，教師把握了教學內容的實質和學生的實際情況，創設情境、設計問題，通過恰當的提問，引導學生積極思考，激發學生的好奇心，努力營造生動活潑的課堂氛圍，形成了有效的學習活動，使學生成為學習的主體，逐步學會學習。學生通過親身參與對核酸檢測分組人數問題的研究，在思考、解決問題和情感態度方面得到發展，在應用中獲得知識技能，鞏固了數學期望的學習，加深了對概念的理解，詮釋了理論聯系實際、學以致用的重要性。同時，借助網絡平臺，鍛煉了學生自主收集信息、查找數據、靈活應用理論知識、解決實際問題的能力，也培養了學生不唯書、不唯上、遇到具體問題冷靜分析、獨立創新的批判精神。