充分挖掘物理思想 提升學生核心素養

李慶國 帥厚梅

（江蘇省揚州市新華中學，江蘇 揚州 22509）

物理思想是物理學科素養的重要組成部分，物理思想對學生科學素養的養成、學習能力的提升有著重要的價值.物理思想教育是物理學科教育的重要組成部分.物理思想是物理學的精髓，是知識轉化為能力的橋梁.在物理教學中教師要引導學生充分挖掘物理思想，使物理思想充分顯現出來，發揮物理思想對學生核心素養的真正培養作用.下面討論了如何充分挖掘教材中、習題中蘊含的物理思想，以達拋磚引玉之用.

1 充分挖掘教材中蘊含的物理思想

1.1 理解重要物理概念建立過程中蘊含的物理思想

物理概念是物理學大廈的基石，在教學中通過實驗器材演示、多媒體的展示等，讓學生概括出物理概念.要讓學生建立物理知識體系，必須充分理解這些概念的內涵與外延.最關鍵的是讓學生理解得出概念的過程中所蘊含的物理思想.只有這樣，才能觸類旁通，才能啟迪思維.下面以“加速度”這一重要概念的得出加以分析.

甲：10m/s→20m/s，用時5s；乙：10m/s→20m/s，用時10s；丙：10 m/s→25 m/s，用時10s.

問題1：比較甲和乙，誰速度增加得快？問題2：比較乙和丙，誰速度增加得快？問題3：比較甲和丙，誰速度增加得快？

在實際教學中發現，對于問題1和問題2學生能順利回答出：甲比乙速度增加快，丙比乙速度增加快.

經詢問，學生的方法為：速度增加量相同時，看時間，時間短即速度增加快；時間相同時，看速度增加量，速度增加量大即速度增加快；學生用的實際上就是“控制變量”的思想.

但對于問題3，學生一時回答不出來，因為甲和丙速度的增加量和用時均不同，控制變量的思想看似不好用.

教師啟發：仍用控制變量的思想，比較甲丙在相同時間內速度的增加量，而相同時間就取單位時間即1s，則甲丙在單位時間內速度的增加量為多少？

問題4：若甲、乙、丙速度變化情況如下，則甲和乙、乙和丙、甲和丙相比誰速度減小得快？

甲：20m/s→10m/s，用時5s；乙：20m/s→10m/s，用時10s；丙：25 m/s→10 m/s，用時10s.

由于有了前述分析，學生能很快給出答案.

總結：當物體的速度發生變化時，有的變化快，有的變化慢，要比較速度變化快慢只要比較即可，若大，則速度變化就快，反之則慢.物理中將命名為“加速度”的實質就是物體在單位時間內的速度變化量，也就是“控制變量”的思想.

“加速度”對于初學者是比較難理解的，在得出概念的過程中主要用了“控制變量”的思想.用這樣的思想，“加速度”概念的得出比較自然，實際教學效果相當好.同時也提問學生，以往學過的哪些概念也是用相同的方法得出的？學生最容易想到的是“速度”.這樣不但學習了新的知識，對學過的內容也是一個很好的回憶和總結，起到“學一個帶一片”的作用.

1.2 理解物理規律的形成過程中蘊含的物理思想

物理規律，是物理學中的靈魂，是物理學大廈中的棟梁，物理學就是利用一個個規律去解決實際問題的學科.一個規律的得出往往要經歷很長的過程.在教學中，讓學生重演重要物理規律的發現過程，讓學生感受科學家探究規律過程表現出來的恒心和毅力，更要讓學生深刻理解物理規律、領悟規律發現過程中所用的物理思想.這對學生產生科學情感、形成科學態度都是大有裨益的.下面以伽利略研究自由落體運動為例加以分析.

自由落體運動究竟是什么性質的運動？在伽利略那個時代，很多科學家都在研究，但都沒有得出令人信服的結論，主要是當時計時技術很難滿足測定自由落體時間的要求.當時進行研究主要在實驗室進行，現在我們知道，若一個小球從5m自由下落，下落時間也就1s左右.一般實驗室高度沒有5m高，故時間太短，較難測量.再說當時是滴水計時，這樣的工具是不能測量自由落體時間的.這就阻礙了對自由落體運動的進一步研究.

伽利略采用了間接實驗的方法，他用一個黃銅小球從阻力很小的斜槽上滑下，并用水鐘測定時間，他經過數百次實驗，發現一個從靜止開始滾下的物體，在連續相等時間間隔內通過的各段距離之比，等于從1開始的一系列奇數之比，即1∶3∶5∶7…結合勻變速直線運動規律可知，小球沿斜槽下滑是勻加速直線運動.

在斜面實驗的基礎上伽利略將斜面的傾角不斷變大，如圖1所示.根據前述結論可知，不管傾角多大都應該是勻加速直線運動，只不過加速度大小不一樣而已.然后將斜面傾角逐漸增大直到90°，小球仍然應該是勻加速直線運動.當斜面變成90°，小球沿槽下滑時跟槽之間沒有力的作用，也就是小球就是做自由落體運動了，即自由落體運動為初速度為0的勻加速直線運動.

圖1

伽利略采用了一個巧妙的方法來“沖淡”重力，小球在斜面上運動的加速度，要比它豎直下落的加速度小得多，所用時間長得多，所以容易測量.在此基礎上再進行合理外推，得到自由落體運動為初速度為0的勻加速直線運動這一重要結論.“弱化”重力真的是一個特別有創意的思想.從斜面外推到豎直，這種合理外推是將實驗和邏輯推理有機結合起來.伽利略“理想斜面實驗”也采用了相同的思想方法.這樣的思想方法開創了物理研究的先河.愛因斯坦和英費爾德在《物理學的進化》中評論說：“伽利略的發現以及他所應用的科學的推理方法是人類史上最偉大的成就之一，而且標志著物理學的真正開端”.

在很多規律得出的過程中，都蘊含著令人拍案叫絕的思想方法，比如庫侖定律的得出.18世紀中期物理學家既沒有度量帶電體所帶電荷量多少的方法，也沒有測量電荷之間非常小的相互作用力的工具.法國人庫侖憑著物理學家敏銳的直覺，斷定一個帶電金屬球與另一個半徑、材料完全相同的不帶電的金屬球接觸后再分開，每球的帶電量應該是原帶電球電荷量的一半，從而巧妙地解決了金屬球所帶電量成倍變化的問題，這種方法可叫作“倍分法”.類似這樣的事例還有很多很多，這里不再一一贅述.

在教學中不但要讓學生體會科學研究的艱難，讓學生對知識有“敬畏感”，更要充分揭示得出規律過程中蘊含的物理思想，讓這些有價值的物理思想方法“浮出水面”.教學過程中教師要將這些隱性的物理思想方法作為教學內容的一部分，將其明朗化、顯性化、條理化地提出來并有機融入知識傳授過程中，啟迪學生的思維，調動和激發學生學習興趣.

1.3 挖掘教材插圖中所蘊含的物理思想

物理教材中有大量的插圖，插圖是一種很好的教學資源.許多插圖中蘊含著很多的物理思想，只有把蘊含的物理思想充分挖掘出來，才能真正發揮插圖的教學作用.

在曲線運動這一節，為了說明物體做曲線運動速度方向，書上有一幅插圖如圖2所示，教師應該引導學生思考圖中蘊含的物理思想：若物體這一段時間內從A運動到B點，則在AB這個過程中平均速度的方向由A指向B，而當B點越來越靠近A，則AB這個過程中平均速度的方向沿AB連線越來越接近A點的切線方向.當B與A點的距離接近0時，則AB平均速度即在A點的瞬時速度方向就是A點的切線方向，由此得到這樣的結論：做曲線運動的物體在某一點瞬時速度方向，沿曲線在這一點切線方向.

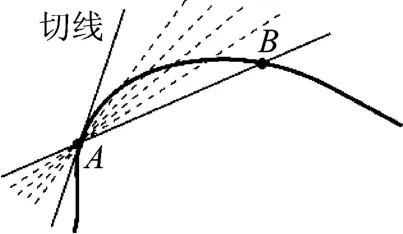
圖2

插圖中蘊含了“極限”的物理思想，將瞬時速度這個比較抽象的問題，用比較直觀的方法進行解決.極限思想對許多具有瞬時性的物理概念的建立均有指導，如瞬時加速度、瞬時功率、瞬時電動勢等.將“極限”思想遷移到物理學其他分支，就能比較順利地實現物理量從平均值到瞬時值的過渡，同時也實現了對物理對象粗略認識到精細認識的升華.

在講彈力的時候，我們知道不管多大的力都可以使物體產生形變，有的形變比較明顯，有點形變比較微小，微小形變怎么能顯示呢？書上有插圖如圖3所示.給桌面施加一個壓力，桌面發生的是微小形變，微小形變放大如何顯示呢？引導學生思考：桌面受力后向下“凹陷”，兩平面鏡由豎直變成傾斜，則經平面鏡反射后的光斑會沿標尺移動.反之，通過光斑的移動，說明桌面發生了形變.

圖3

通過光斑移動來間接的顯示桌面的形變，這是一個“轉化”的思想，也是一個“放大”的思想.可以再激發學生思考，為什么要用二次反射呢？這是多次放大的思想.同時可以再啟發學生思考，還有很多地方也是用這樣的方法.比如說一個電路中是否有電流，你們無法用肉眼觀察到，可以看燈泡是否亮，也可以看串在電路中的電流表的指針是否偏轉.這樣的例子還有很多.通過這些思想將“看不見摸不著”的東西直觀的顯示出來，這就是一種重要的思想.

教材插圖是教學內容的一個重要補充，教師在教學中要充分運用這些素材，挖掘插圖中所蘊含的物理思想，真正發揮插圖的教學功能，提升學生能力，更好落實物理學科核心素養.

2 充分挖掘習題中蘊含的物理思想

2.1 體會題目設計中包含的物理思想

例1.跳傘運動員做低空跳傘表演，他在離地面224m高處，由靜止開始在豎直方向做自由落體運動，一段時間后，立即打開降落傘，以12.5m/s2的平均加速度勻減速下降，為了運動員的安全，要求運動員落地的速度最大不得超過5m/s（g取10m/s2），問：

（1）運動員打開傘時，離地面高度至少為多少？

（2）運動員著地時速度為5m/s，則相當于從多高處自由落下？

解析：第（1）問不再討論，著重討論第（2）問，求解方法很多，故過程忽略，結果為1.25m.第（2）問應該說很簡單，出題者究竟想考我們什么？難道僅僅是為了考查學生對基本公式的運用嗎？在實際教學中我的確提出過這個問題，學生面面相覷，無法回答.

落地速度太大，人會受傷，但通常人對速度的大小，可能沒有太大的感覺，而對長度、高度可能感覺更直觀一些.如果人從高1.25m的墻上跳下是否會受傷，學生應該可以輕易判斷的.

題目的本意是讓我們體會轉化的思想，把對速度大小比較抽象的認識轉化為對高度比較直觀的認識.在這問中還體現了把所學知識應用于生活的思想，知識不會應用就是“無用”的知識.

例2.水分子直徑約為4×10-10m，若把9g水的分子一個挨一個緊密排成單行，則可繞地球赤道約多少圈？（赤道周長約為4×10-10m）

解析：水的摩爾質量為18g/m o l，則9g為0.5m o l，近似取NA=6×1023m o l-1，則水分子總數n=0.5NA=3×1023，則一個挨一個緊密排成單行，總長s=n d=1.2×1014m，則繞赤道的圈數為

通過這個題目讓學生熟悉與阿伏伽德羅常數相關的計算，想說明組成物質的分子數是大量的.哪怕是看似很小的宏觀物體，組成它的分子數也是大量的，但大量怎么體現呢？因為分子是很小的，肉眼看不出，故對大量沒有直觀印象.題目通過轉化的思想將“大量”通過繞赤道的圈數來體現，一是將“大量”直觀化，二是通過繞赤道的圈數之多讓學生更加理解組成物體的分子是“大量”的概念.轉化成一個宏觀的現象，可能會讓學生更感震撼.這樣對阿伏伽德羅常數，對大量的概念會理解得更深.在教學中若想讓學生更震撼，理解更深，還可以再進行補充，如學生1s喝進去1000 0個水分子，9g水需要多長時間才能喝完？通過計算，一年若按365天算，則喝完9g水約需9.5×1016年.這樣學生對“大量”應該會徹底理解到位，可能一輩子也不會忘.

只有充分理解題目中所包含的物理思想，才能將題目的真正作用發揮出來，才能體現題目的價值，否則就是為了解題而解題，顯得枯燥無味，也就失去了學習物理的真正的意義和作用.

2.2 在題目分析中凸顯物理思想

為了鞏固所學知識，解題是必不可少的，但關鍵是在題目分析時，一定要凸顯解題的物理思想.這樣對學生的學習才有幫助，才能使學生在解決問題時養成思考習慣，學習力才能不斷增強，下面舉一例說明.

例3.運動學中有人認為引入“加速度的變化率”沒有必要，然而現在有人指出“加速度的變化率能引起人的心理效應，車輛的平穩加速（即加速度基本不變）使人感到舒服，否則人感到不舒服.關于“加速度的變化率”，下列說法中正確的是

（A）從運動學角度的定義，“加速度的變化率”的單位應是m/s3.

（B）加速度的變化率為0的運動是勻速直線運動.

（C）若加速度與速度同方向，a-t圖像如圖4所示，表示的是物體的速度在減小.

（D）若加速度與速度同方向，a-t圖像如圖4所示，已知物體在t=0時速度為5m/s，則4s末的速度大小為17m/s.

圖4

解析：在實際教學中發現，（A）、（B）、（C）選項以大多數學生的能力都能準確判斷，但（D）選項感到困難.在解決此問題時，我為學生設立了一個臺階，模仿（D）選項的問題：若物體加速度與速度同方向，a-t圖像如圖5所示，已知物體在t=0時速度為5m/s，則4s末的速度大小為多少？

圖5

對于這個問題，學生很快就給出了答案.再問學生4 s內物體速度的增加量多大？圖像與坐標軸圍成的面積的值是多少？能找出他們之間的關系嗎？學生們都得到了“圖像與坐標軸圍成的面積的值等于物體速度的增加量”這一結論.接著再問，能不能把這個結論直接遷移到圖6這種情況？此時出現了不同答案，有的說行，有的說不行.筆者不置可否.

圖6

提示學生將物體運動時間平均分成n段（n→∞），每一段時間為Δt，如圖6所示.由于每一段時間極短，故可認為在每一段極短時間內加速度是恒定的，故由前述結論可知：圖像與坐標軸圍成的面積的值等于物體速度的增加量.依此類推，每一個Δt均有同樣的結論，故可得到0—4s內圖像與坐標軸圍成的面積的值等于4s內物體速度的增加量，計算可得Δv=12m/s，即4s物體速度為17m/s.

得出結果后，一定還要跟學生講清分析過程中運用了如下物理思想.

（1）用勻變速結論推出非勻變速結論，充分體現了用已知推未知，從簡單到復雜的物理思想.

（2）將運動時間無限分段，即使全過程加速度是變的，但每一段可以認為是恒定不變.這樣在每一段就可以運用已有結論，充分體現了“化變為恒”的思想.

（3）無限分割實際使用的也就是“微元”的思想.“微元法”在中學階段用得也很多，教師也可以借機讓學生回憶一下，在推導勻變速直線運動的位移與時間關系時就用了“微元法”.這樣學生就覺得有似曾相識之感，接受起來就不會覺得很陌生.

在進行題目分析時，一定要將所用的物理思想凸顯出來，一是讓學生體會運用知識解決問題的過程.二是讓學生感知知識的魅力，不斷引導學生學會思考，激發斗志，最終達到能力的提升.

物理思想是物理知識及物理方法的靈魂.物理思想具有隱蔽性、抽象性和創造性，它蘊含在知識的發生、發展和應用的過程中.傳統物理教學往往是重視必考知識的傳授和解決能力的培養.隨著新課程改革的實施，教師一定要改變這種狀況.只有使學生在進行物理課程學習時，深入到對于物理思想的了解和挖掘，才能夠形成系統的、完善的物理學科學習理念.掌握物理學習的精髓，才能夠為學生今后的發展開辟一個全新的學科領域，真正使學生感受到物理的奧秘和魅力.