空化泡表面附近馬蘭戈尼力的數值模擬研究

王小伍，李雙君，虎驍

(華南理工大學物理學院，廣州 510640)

由于表面張力與溫度有關，當表面溫度不一致時，將在表面上產生熱毛細力，受這個切向應力作用，液體形成馬蘭戈尼(Maragoni)對流或熱毛細對流。在薄膜噴涂[1]、液滴蒸發[2]和熔體單晶生長[3]等領域中，馬蘭戈尼對流或熱毛細對流起到重要作用。

一般液體的表面張力都隨溫度升高而降低，因此溫度高的地方表面張力相對較小，該處的流體就會向溫度低的地方流動。在一些換熱設備中，工質需要由溫度較低處流回溫度較高處，以實現工質的循環，如果以一般液體為工質，馬蘭戈尼對流使得液體由溫度較高處流回溫度較低處，此時馬蘭戈尼對流將不利于換熱。一些醇類水溶液表面張力與溫度的關系與一般液體不同，在一定濃度和溫度范圍內，其表面張力隨溫度升高而增大[4]，從而將形成由溫度較低處到溫度較高處的馬蘭戈尼對流，這種對流與換熱設備要求的液體循環方向一致，能增強換熱設備的傳熱性能。

在超聲波作用下，當液體局部壓力低于某一臨界壓力時，液體內部或液固界面處產生空化泡，在超聲場和熱動力聯合作用下，空化泡將經歷膨脹、收縮和崩潰。本文研究了超聲波在2.5%的正戊醇水溶液和純水中產生的空化泡的氣液界面附近的馬蘭戈尼力，以期為進一步研究超聲波強化傳熱提供參考。

1 物理數學模型

根據陳淑玲等[4]的實驗研究，在一定溫度范圍內，2.5%的正戊醇水溶液的表面張力隨溫度增加而增大的現象較為明顯，由最小二乘法擬合得到的2.5%的正戊醇水溶液的表面張力σ與溫度T的關系為：

σ=[0.016 7×(T-273)2-1.268(T-273)+48.714)]×10-3

(1)

如圖1(a)所示，簡化后的空化泡模型為附著在固體表面的一球冠狀氣泡，在超聲波的作用下氣泡半徑r隨時間發生變化。假設：1)空化泡球心固定并保持以球心對稱；2)液體不可壓縮；3)忽略重力作用和擴散作用；4)泡內氣體為理想氣體；5)除了表面張力，空化泡外的液體和空化泡內的氣體的物理特性均為常數。如圖1(b)所示，空化泡壁附近存在一厚度為δ的熱邊界層，空化泡內氣體通過熱邊界層與周圍液體進行熱量交換。

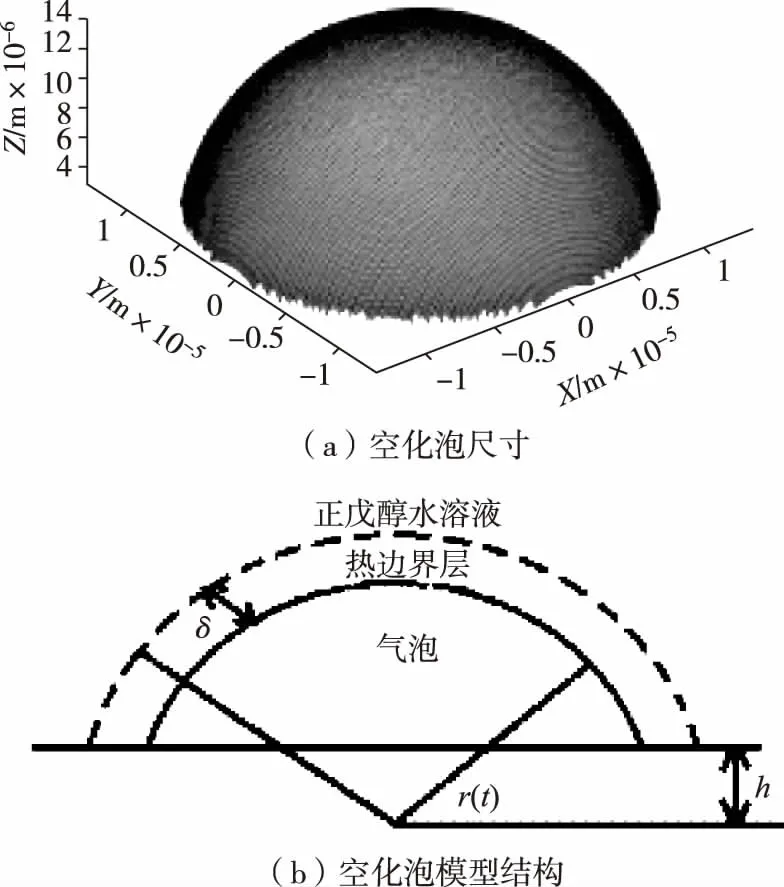
圖1 空化泡物理模型

空化泡邊界方程：

x2+y2+z2=r(t)2z>h

(2)

式(2)中，h為球心到達空化泡附著固體面的距離。r(t)為某時刻空化泡半徑，滿足方程：

(3)

式(3)中，ρl、ρv分別為液體、空化泡內氣體的密度；c為液體中的聲速；pwall及pfar分別為空化泡壁外側及遠處液體中的壓強，pwall滿足方程：

(4)

式(4)中，r0為空化泡初始半徑；γ為空化泡內氣體的絕熱指數；μ為粘滯系數；pv為空化泡內的蒸汽壓。若將空化泡內氣體視為理想氣體，pv可以根據理想氣體狀態方程近似求得。

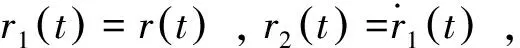
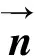
(5)

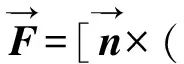
(6)

熱邊界層內與球心距離為r'處某點的溫度Tδ為：

(7)

式(7)中，Twall、Tfar分別為空化泡壁和遠處液體的溫度。空化泡壁溫度為：

(8)

式(8)中，kl、kg分別為液體和空化泡內氣體的導熱系數；Tc為空化泡中心的溫度，將空化泡的膨脹、壓縮視為理想氣體絕熱過程，Tc可以根據理想氣體絕熱過程方程算得。

空化泡內與球心距離為r'的某點的溫度Tr為：

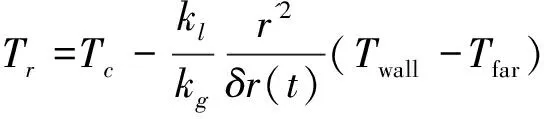
(9)

計算中用到的相關參數取值為：Tfar=353 K，ρl=1 000 kg/m3，ρv=1.205 kg/m3，pv=3.169×103MPa，c=1 483m/s，pfar=1.013×105Pa，μ=1.022×104kg·s/m3，超聲波聲壓p=-pmsin2πft，pm取為0.5 MPa，f為超聲波頻率，本文取為20 kHz。

2 結果與討論

空化泡半徑隨時間的變化如圖2所示，從圖2中可以看出，一開始空化泡半徑隨時間增大，達到峰值以后急速減小。當t為9.9×10-6s時，空化泡處于膨脹狀態，空化泡內溫度低于遠處液體溫度；當t為23.6×10-6s時，空化泡處于壓縮狀態，空化泡內溫度高于遠處液體溫度。

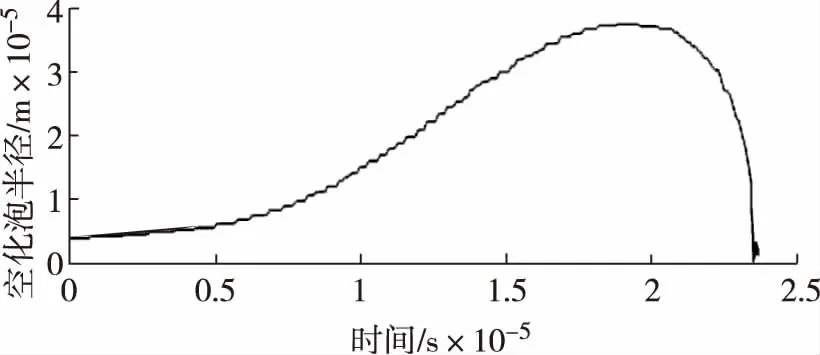
圖2 空化泡半徑隨時間的變化

圖3為t=9.9×10-6s時熱邊界層和空化泡內的溫度分布。從圖3可見，隨著與球心距離的增加，邊界層內溫度增加，溫度梯度值減小，在接近外部正戊醇水溶液時趨近于遠處液體溫度。隨著與球心距離的增加，空化泡內溫度增加，溫度梯度值變大。

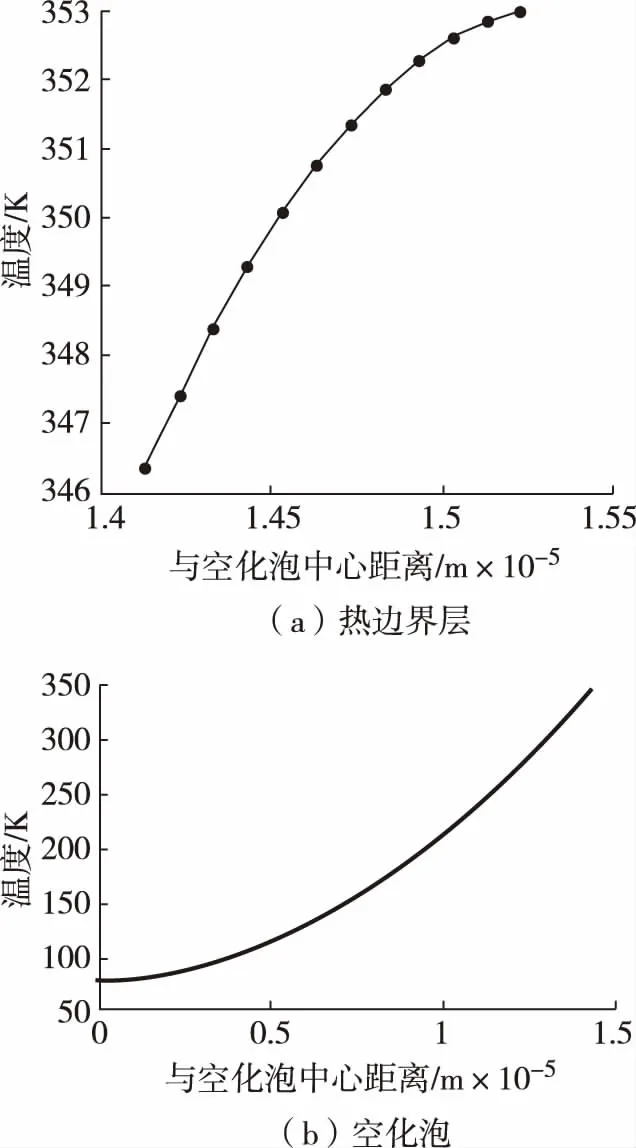
圖3 時間為9.9×10-6 s時熱邊界層和空化泡內溫度分布

圖4為t=23.6×10-6s時熱邊界層和空化泡內的溫度分布。從圖4可見，隨著與球心距離的增加，邊界層內溫度減小，溫度梯度值減小，在接近外部正戊醇水溶液時趨近于遠處液體溫度。隨著與球心距離的增加，空化泡內溫度減小，溫度梯度值變大。

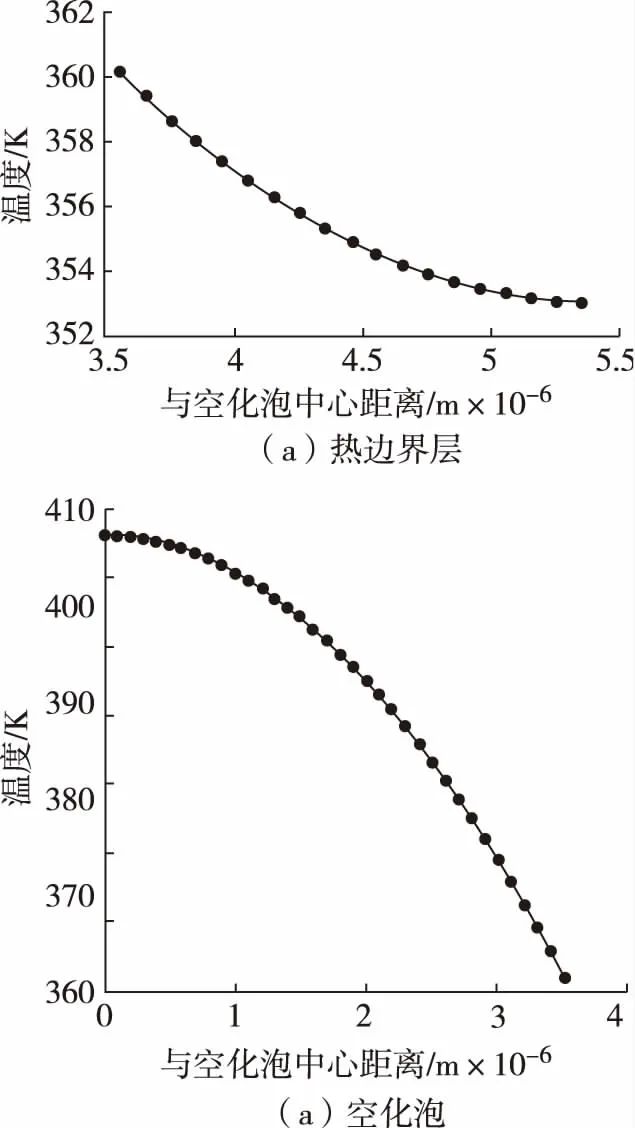
圖4 時間為23.6×10-6 s時熱邊界層和空化泡內的溫度分布

圖5為t=9.9×10-6s時2.5%的正戊醇水溶液中的空化泡壁面附近的馬蘭戈尼力。從圖5可見，空化泡壁面附近沿X軸和沿Y軸方向的馬蘭戈尼力呈馬鞍狀分布，除x>0且y>0區域的部分位置外，馬蘭戈尼力的方向均指向坐標軸正軸；等高線呈拋物線狀，沿X軸方向的馬蘭戈尼力的等高線開口向X軸正方向，沿Y軸方向的馬蘭戈尼力的等高線開口向Y軸正方向。空化泡壁面附近沿Z軸方向的馬蘭戈尼力呈勺狀分布，以y=x平面對稱，y>0且x>0區域的馬蘭戈尼力小于y<0且x<0區域的，大部分區域的力的方向指向Z軸正軸，部分y>0且x>0區域的力的方向指向坐標軸負軸，部分等高線為閉合曲線。由矢量圖可知，大部分區域的馬蘭戈尼力的方向指向空化泡外側。

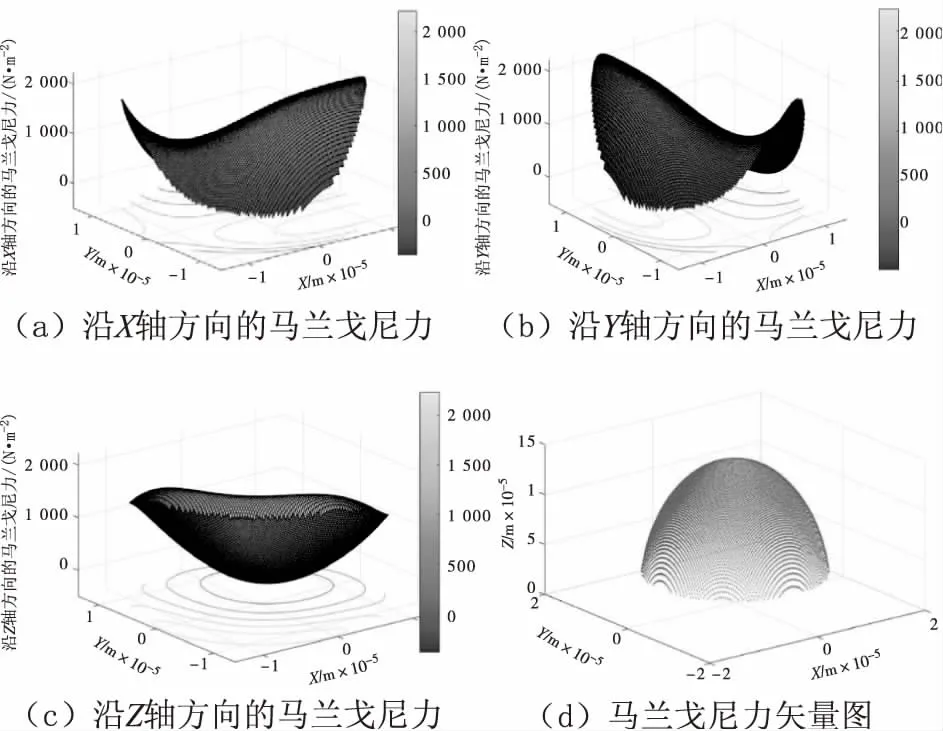
圖5 時間為9.9×10-6 s時2.5%的水溶液中的空化泡壁面附近的馬蘭戈尼力

圖6(a)給出的是t=9.9×10-6s時，純水中的空化泡壁面附近的馬蘭戈尼力。從圖6可見，空化泡壁面附近沿X軸和沿Y軸方向的馬蘭戈尼力呈馬鞍狀分布，除x>0且y>0的部分位置外，馬蘭戈尼力的方向均指向坐標軸負軸；等高線呈拋物線狀，沿X軸方向的馬蘭戈尼力的等高線開口向X軸正方向，沿Y軸方向的馬蘭戈尼力的等高線開口向Y軸正方向。空化泡壁面附近沿Z軸方向的馬蘭戈尼力呈倒置的勺狀分布，勺把向Z軸正反向翻轉，以y=x平面對稱，部分y>0且x>0位置的馬蘭戈尼力指向Z軸正軸，其它區域的馬蘭戈尼力均指向Z軸負軸，部分等高線為閉合曲線。由矢量圖可知，大部分區域的馬蘭戈尼力的方向指向空化泡內側。

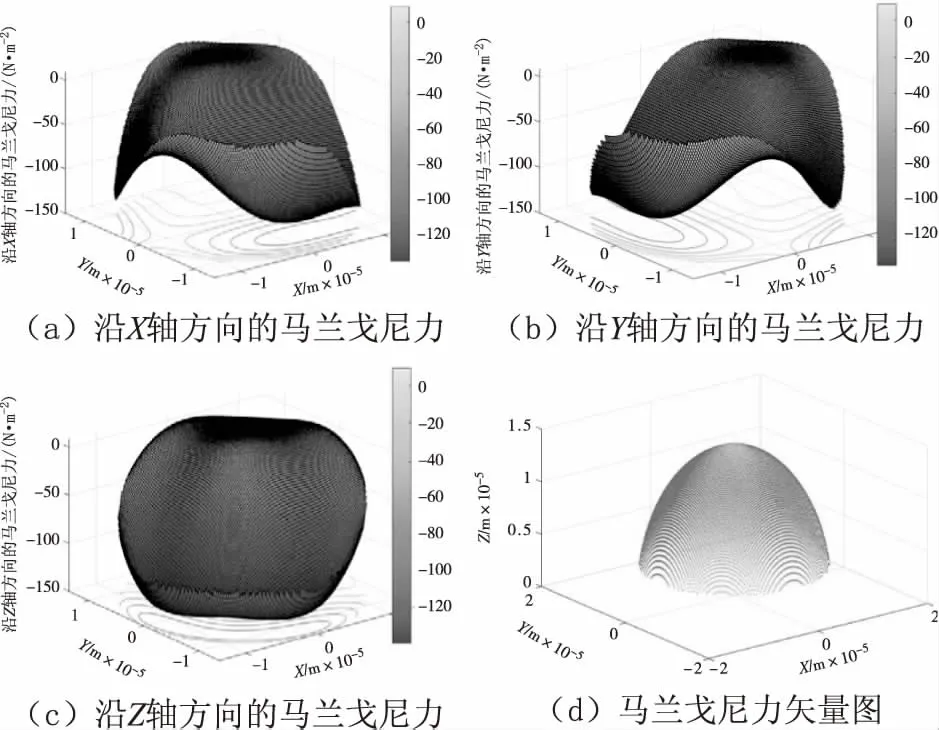
圖6 時間為9.9×10-6 s時純水中的空化泡壁面附近的馬蘭戈尼力

對比圖5和圖6可見，2.5%的正戊醇水溶液中的空化泡壁面附近的馬蘭戈尼力要遠遠大于純水中的馬蘭戈尼力，因此，2.5%的正戊醇水溶液中由馬蘭戈尼力引起的對流強度也將較大。此外，由于2.5%的正戊醇水溶液中的表面張力對溫度的相關特性與純水中的不同，兩種液體中沿X、Y以及Z軸方向的馬蘭戈尼力的方向相反，因此由馬蘭戈尼力引起的對流方向也將不同。由于t=9.9×10-6s時，空化泡正處于膨脹期，熱邊界層內溫度沿徑向增加，2.5%的正戊醇水溶液中的馬蘭戈尼力指向空化泡外側，由此引起的馬蘭戈尼對流有利于空化泡膨脹以及熱量傳遞。

圖7 為t=23.6×10-6s時2.5%的正戊醇水溶液中的空化泡壁面附近的馬蘭戈尼力。從圖7可見，空化泡壁面附近沿X軸和沿Y軸方向的馬蘭戈尼力仍舊呈馬鞍狀分布，方向均指向坐標軸正軸。在y<0區域，沿X軸方向的馬蘭戈尼力的等高線呈拋物線狀，開口指向X軸正方向；在y>0區域，沿X軸方向的馬蘭戈尼力的等高線為不相交的曲線。在x<0區域，沿Y軸方向的馬蘭戈尼力的等高線呈拋物線狀，開口指向Y軸正方向；在x>0區域，沿Y軸方向的馬蘭戈尼力的等高線為不相交的曲線。空化泡壁面附近沿Z軸方向的馬蘭戈尼力呈倒置的勺狀分布，以y=x平面對稱，y<0且x<0區域的力的方向指向Z軸正軸，部分y>0且x>0區域的力的方向指向Z軸負軸。由馬蘭戈尼力的矢量圖可知，部分位置的馬蘭戈尼力的方向指向空化泡內側。

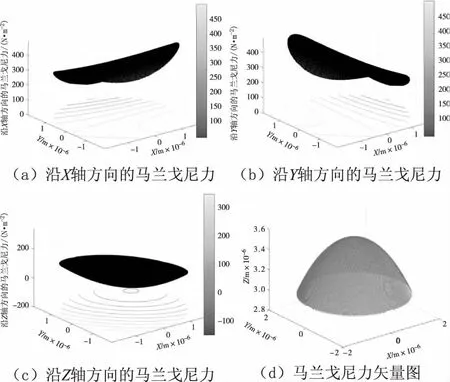
圖7 時間為23.6×10-6 s時 2.5%正戊醇水溶液中的空化泡附近的馬蘭戈尼力

對比圖5和圖7可以發現，在t=9.9×10-6s、t=23.6×10-6s時，雖然2.5%的正戊醇水溶液中的沿X與Y軸方向的馬蘭戈尼力分布輪廓均呈現馬鞍狀，沿Z軸方向的馬蘭戈尼力分布輪廓均呈倒置的勺狀，但對應t=23.6×10-6s時的馬鞍平坦，勺把也沒有反向翻轉，這是由于在t=23.6×10-6s時，空化泡迅速收縮，邊界層厚度較大，溫度梯度值較小，因此，t=23.6×10-6s時的馬蘭戈尼力要遠遠小于t=9.9×10-6s時的馬蘭戈尼力，由此產生的馬蘭戈尼對流強度也將小于膨脹時的對流強度。此外，t=23.6×10-6s時，沿Z軸負方向的馬蘭戈尼力對應的區域增加，即指向空化泡內側的馬蘭戈尼力對應的區域增加，由于此時空化泡處于壓縮期，指向空化泡內側的馬蘭戈尼力有利于空化泡壓縮以及熱量傳遞。

3 結語

正戊醇水溶液表面張力隨溫度的變化關系與純水不同，本文研究了超聲波在2.5%的正戊醇水溶液中產生的空化泡的氣液界面附近的馬蘭戈尼力，并與純水中的空化泡的氣液界面附近的馬蘭戈尼力進行了比較。主要結論如下：

(1)空化泡膨脹時，2.5%的正戊醇水溶液和純水中的空化泡壁面附近的馬蘭戈尼力的分布輪廓相似，但方向相反，2.5%的正戊醇水溶液中的空化泡壁面附近大部分區域的馬蘭戈尼力指向空化泡外側。此外，2.5%的正戊醇水溶液中的馬蘭戈尼力要遠遠大于純水中的馬蘭戈尼力，由馬蘭戈尼力引起的對流強度也將較大，有利于空化泡膨脹以及熱量傳遞。

(2)空化泡收縮時，相比膨脹時，2.5%的正戊醇水溶液中的空化泡壁面附近更多的區域的馬蘭戈尼力的方向指向空化泡內側。由于空化泡收縮時，熱邊界層厚度較大，溫度梯度值較小，因此，2.5%的正戊醇水溶液中空化泡受到的馬蘭戈尼力小于其在膨脹時受到的馬蘭戈尼力，由此產生的馬蘭戈尼對流強度也將小于空化泡膨脹時的馬蘭戈尼對流強度。