雙太陽翼GEO 衛星在軌角動量管控方法

洪振強，俞 潔，劉 偉，楊立峰，陸國平，施晨康，趙 輝

（1.上海衛星工程研究所，上海 201109；2.上海航天技術研究院，上海 201109）

0 引言

地球同步軌道（Geosynchronous Earth Orbit，GEO）三軸穩定衛星在軌穩態輪控模式下，通過飛輪吸收環境干擾力矩，保持衛星姿態穩定。在環境力矩的作用下，飛輪角動量存在隨時間累積項，需要定期進行角動量卸載，避免飛輪轉速飽和。目前，國內外針對航天器環境干擾和動力學特性的在軌辨識已經開展了廣泛研究。文獻［1］提出了一種利用光壓力矩輔助衛星太陽電池翼角度調整進行角動量管控的方法，但該卸載方法僅對對日定向衛星適用。文獻［2］設計了一種基于以飛輪極限角動量為參考的零運動力矩分配輪系角動量管控策略，主要目的是避免系統角動量未達到包絡面時部分飛輪角動量出現飽和。文獻［3］的研究對象限定在采用慣性系為控制基準的航天器角動量管理。文獻［4］主要解決引力梯度力矩和氣動力矩常值部分帶來的角動量積累問題。文獻［5］采用引力梯度力矩平衡姿態，設計了基于極點配置的空間站角動量管理控制器。文獻［6］對環月地軌道環繞衛星所受重力梯度力矩進行了分析。文獻［7］研究了當軌控推力器存在大力矩擾動時系統角動量管控方法。文獻［8］研究了角動量管理對衛星軌道的影響，但均不涉及太陽光壓力矩。文獻［9］研究電推進衛星通過將推力器的指向略微偏離質心來產生控制力矩，完成角動量卸載。文獻［10］設計了一種基于氣動力矩和模型預測的低地軌道（Low Earth Orbit，LEO）衛星角動量管控算法，但不適用于GEO 衛星。文獻［11］用幾何方法詳細討論了航天器各表面受曬的情況，推導了不同太陽光入射條件下航天器各面所受到的太陽光壓力矩數學模型。文獻［12］提出一種精確求取太陽光壓有效作用面積的方法。文獻［13］對太陽光壓力矩與大氣阻力力矩的建模與仿真提出了新的方法，準確地對太陽光壓力矩與大氣阻力力矩進行了估計。文獻［14］論述了大型三軸氣浮臺轉動慣量和干擾力矩高精度聯合辨識技術，但需要進行主動激勵，不便于在軌操作。文獻［15］闡述了導航衛星太陽光壓建模方法與模型特性分析，主要研究太陽光壓對軌道攝動的影響，而不是姿態控制的影響。本文針對對稱布局GEO衛星角動量緩慢累積的特點，開展在軌環境力矩辨識和角動量管控研究，可為姿控系統的精細化設計提供參考依據，并以此為基礎提出使用3 臺飛輪接入閉環控制狀態下的角動量管控策略，延長角動量卸載周期。

1 慣性系下角動量模型

靜止軌道衛星運行在穩態輪控模式時，通過飛輪吸收外界干擾力矩而保持衛星姿態三軸穩定。由于地球靜止軌道高度達到36 000 km，地磁力矩和大氣阻尼力矩可以忽略不計，只需要考慮太陽光壓和重力梯度力矩的影響。

1.1 太陽光壓干擾力矩

關于太陽光壓力矩，已經在很多文獻中進行了詳細的推導和描述。本文的目的是在慣性坐標系中建立太陽光壓干擾模型，提取特征參數，為在軌精確辨識奠定基礎。單邊太陽翼與雙邊對稱太陽翼的太陽光壓力矩分析方法一致，其最大區別是太陽光壓壓心和衛星質心距離存在較大差別。

以雙邊對稱太陽翼為例建立太陽光壓干擾力矩模型，如圖1 所示。由于角動量守恒定理須在慣性系下描述，因此，首先建立慣性參考系

O

X

Y

Z

，其原點

O

位于衛星質心，

O

X

指向衛星星下點時刻為12：00 對應的飛行方向，

O

Y

沿軌道負法向，

O

Z

、

O

X

和

O

Y

滿足右手定則。設太陽光壓壓心在

O

X

Y

Z

坐標系中的初始位置矢量為

P

=[

P P P

]，太陽光壓法向力為

F

=[0 0

F

]，切向力為

F

=[0

F

0]，力的大小與太陽光入射角

α

的關系見文獻［1］。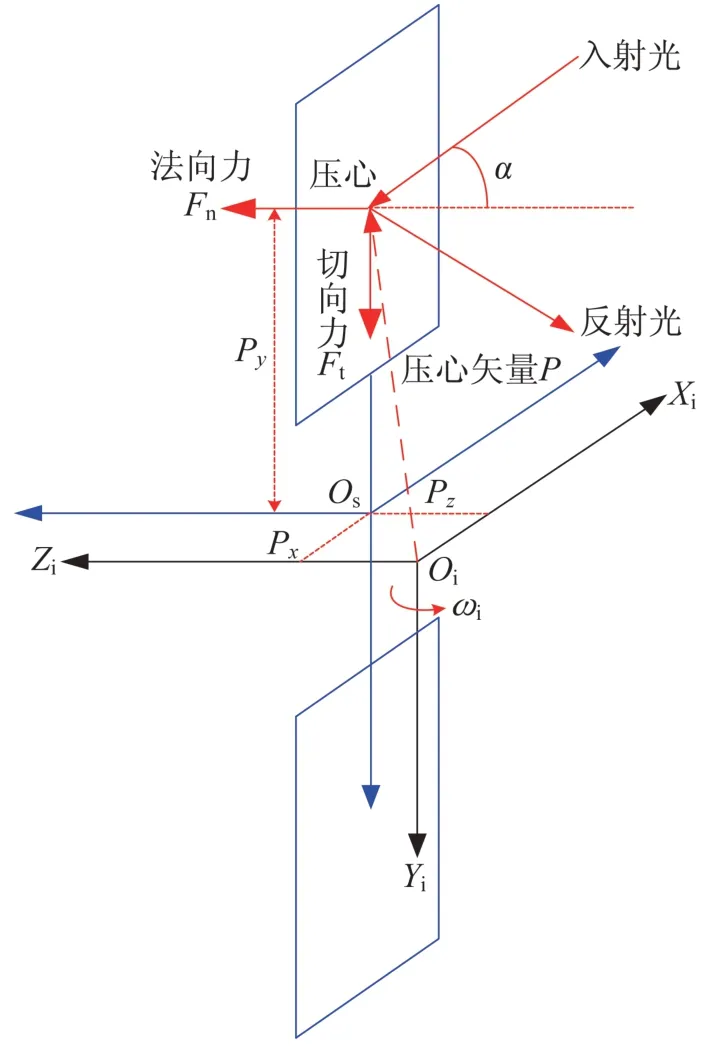

圖1 太陽光壓作用示意圖Fig.1 Schematic diagram of solar pressure effects

設慣性系中太陽光壓力矩為

T

，其可根據太陽光壓力和壓心矢量計算得到。由于壓心矢量隨衛星的軌道運動相對慣性空間旋轉，所以先計算時變的壓心矢量：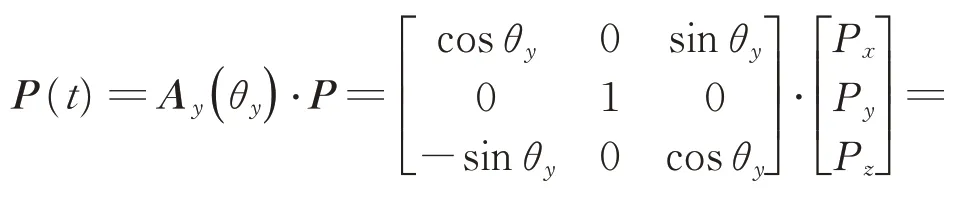

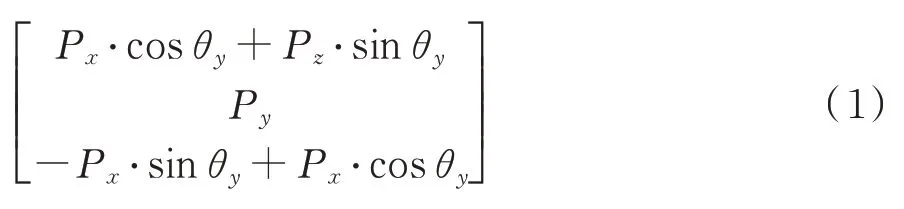
式中：

A

(

θ

)為繞

y

軸的旋轉矩陣；旋轉角

θ

與軌道角速度相關。對于GEO 衛星，可直接由軌道角速度

ω

乘以時間得到。進一步可得慣性系下時變的太陽光壓力矩

T

(

t

)為

1.2 重力梯度干擾力矩

對于圓軌道衛星，在小姿態情況下，衛星本體坐標系下的重力梯度力矩

T

可表示為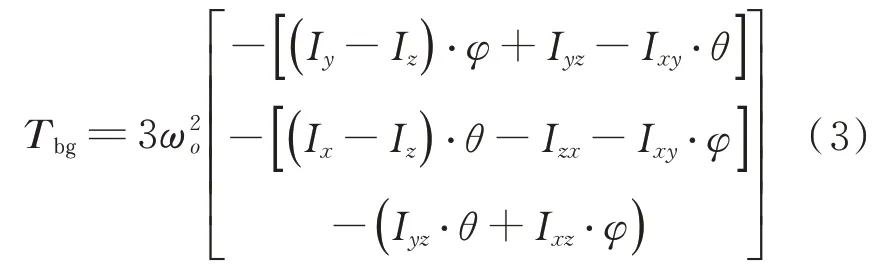

式中：

φ

、

θ

分別為衛星的滾動角和俯仰角。從而可得慣性系中的重力梯度力矩

T

(

t

)為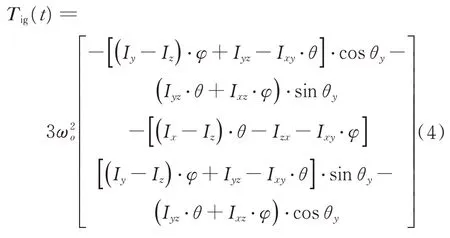

穩態輪控下，衛星本體坐標系與軌道坐標系近似重合，即

φ

≈

θ

≈0，因此，式（4）可簡化為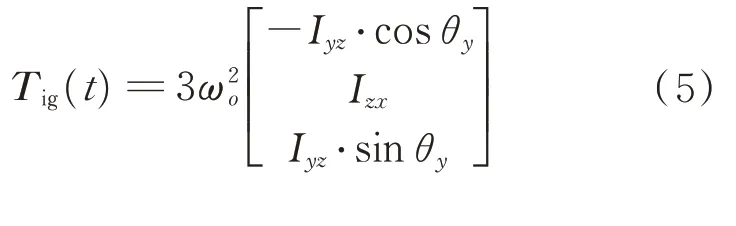

1.3 整星角動量積累模型

根據角動量守恒定理，在慣性系下對干擾力矩進行積分即可得到慣性系中的角動量變化曲線。設慣性系中的角動量為

H

=[

H

H

H

]，有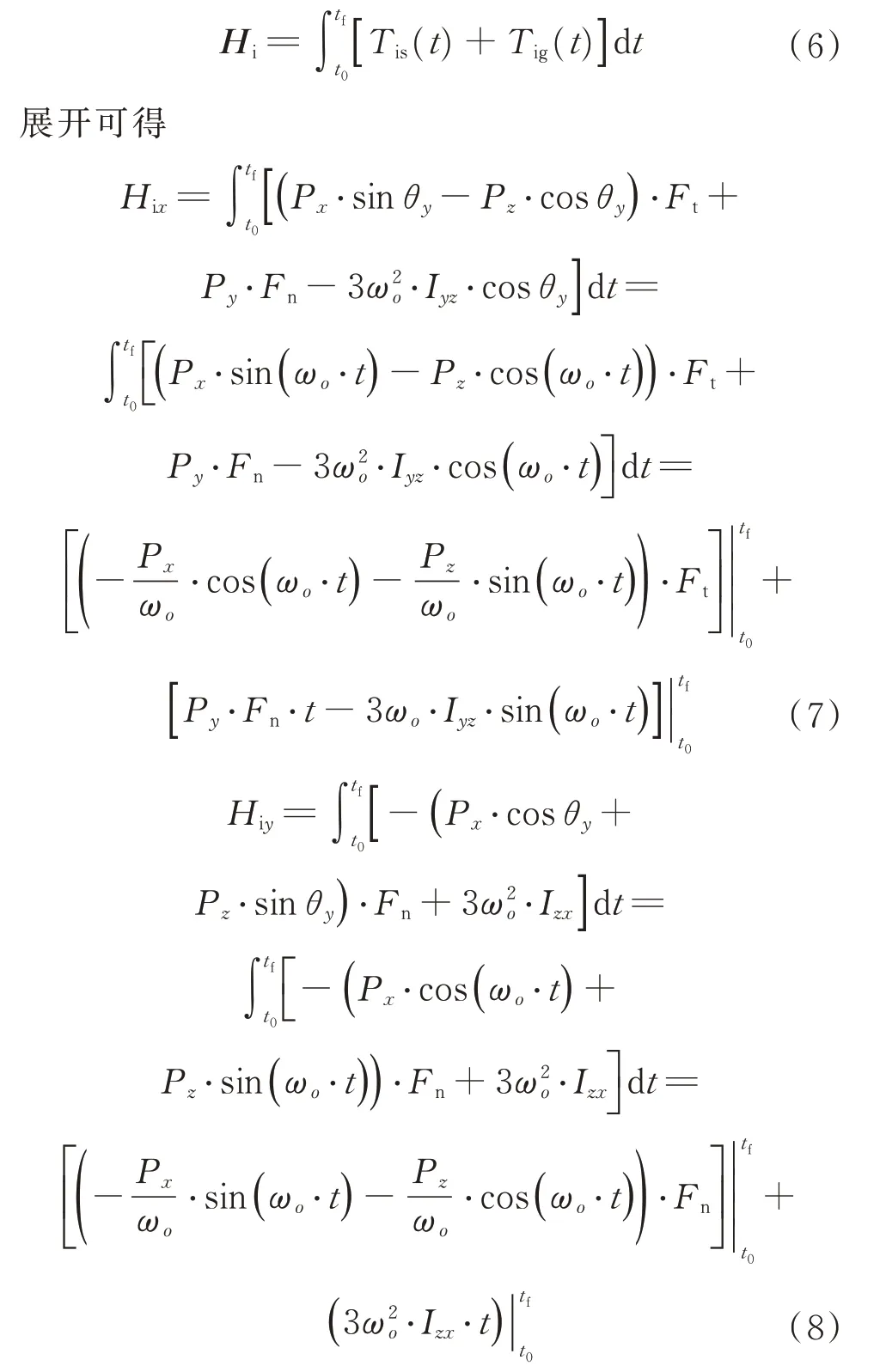

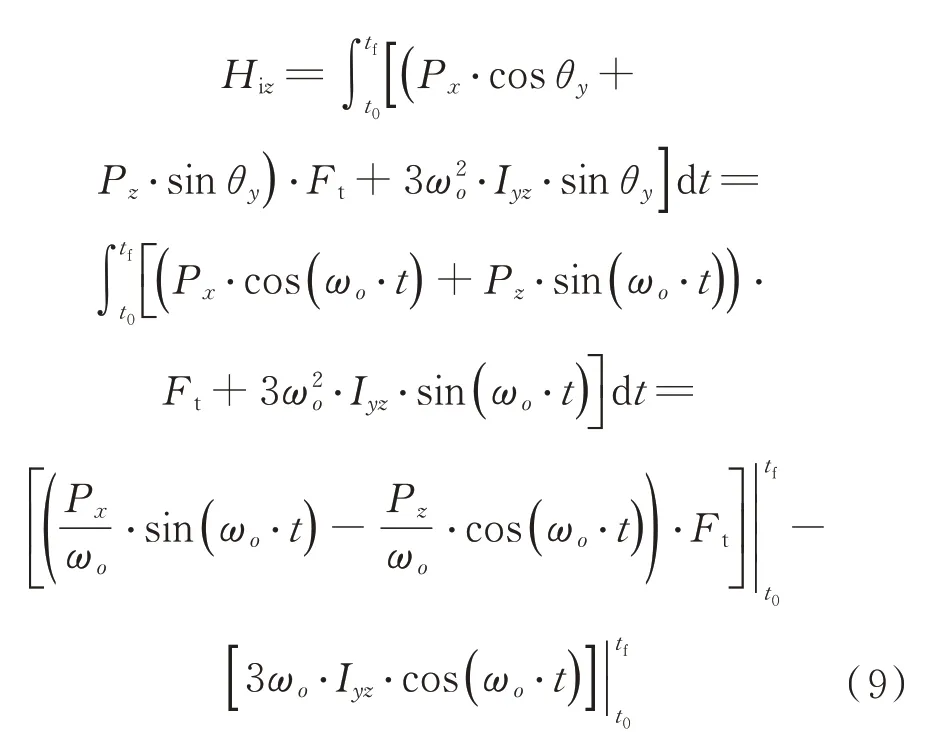
進一步，結合衛星的軌道和姿態運動，可將慣性系中的角動量映射到衛星本體系中，得到衛星本體系下的角動量

H

=[

H

H

H

]，對于GEO衛星，有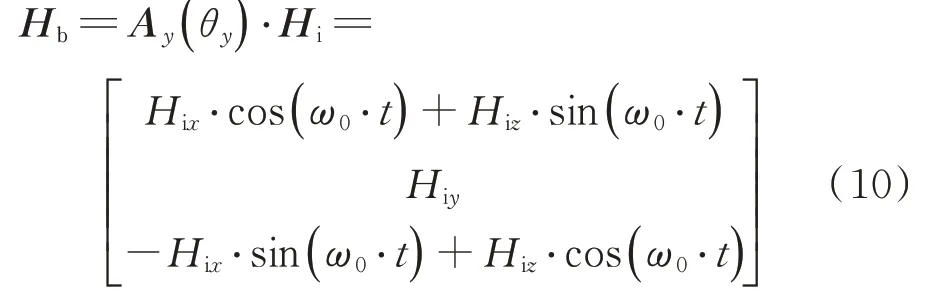

經上述分析，可得GEO 軌道衛星環境干擾力矩特性，見表1。

X

、

Z

軸合成角動量反映了太陽光壓干擾力矩的累積效應，

Y

軸角動量反映了重力梯度力矩的累積效應。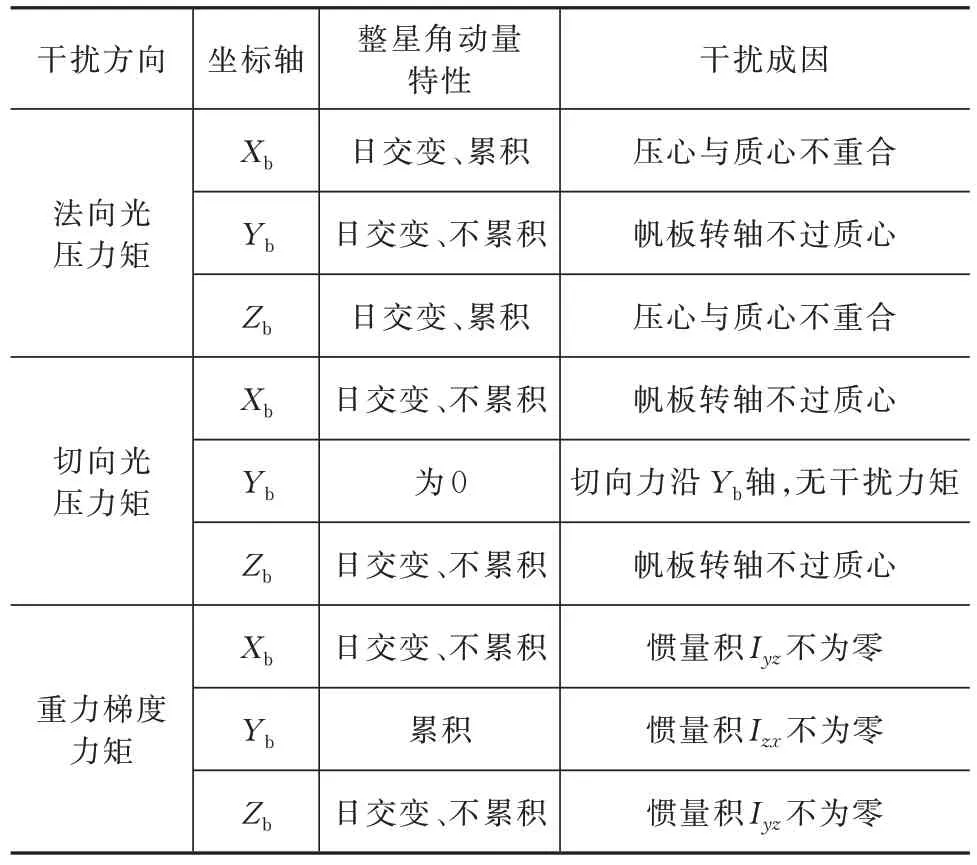

表1 GEO 軌道環境干擾力矩分析總結表（相對軌道系零姿態時）Tab.l Analysis summary of GEO orbit environment disturbance torques（relative to the zero attitude of the orbit system）

2 環境干擾力矩辨識

2.1 辨識算法

根據慣性系下的角動量模型式（7）和式（8），其中，式（7）反映了法向太陽光壓引起的角動量累積和切向太陽光壓及重力梯度力矩引起的角動量交變，式（8）反映了重力梯度力矩引起的角動量累積和切向太陽光壓引起的角動量交變。提取特征參數，改寫環境干擾角動量累積模型如下：

式中：

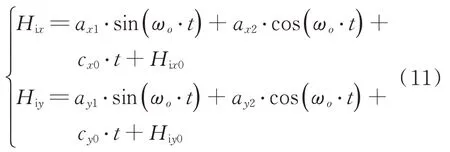
H

、

H

分別為

X

向和

Y

向的初始角動量；特征參數

a

、

a

、

c

、

a

、

a

、

c

分別為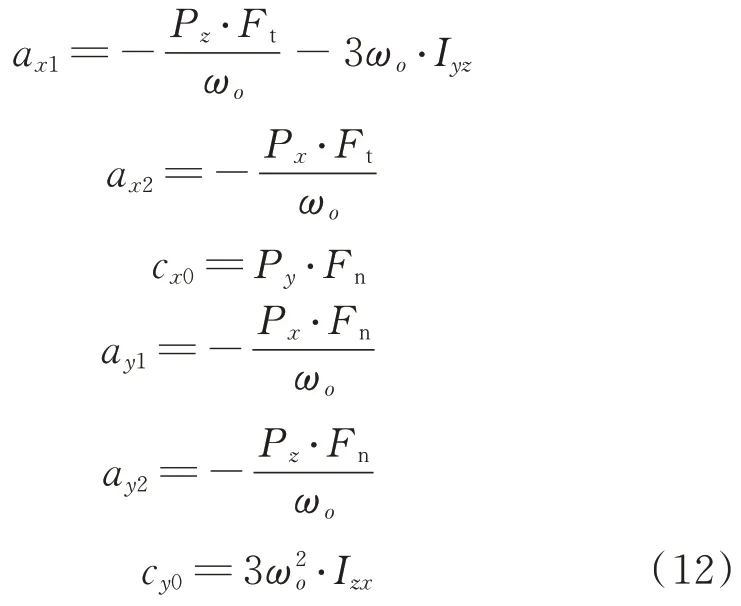

根據上述模型，結合在軌遙測數據，采用最小二乘擬合即可得到各特征系數。根據特征參數，可計算得到法向和切向太陽光壓力引起的干擾力矩辨識結果如下：

結果1，法向太陽光壓力引起的繞

O

X

軸干擾力矩，

P

?

F

=

c

；結果2，法向太陽光壓力引起的繞

O

Y

軸干擾力矩，

P

?

F

=-

a

?

ω

；結果3，切向太陽光壓力引起的繞

O

Z

軸干擾力矩，

P

?

F

=-

a

?

ω

；

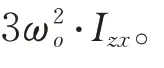
2.2 辨識結果

根據飛輪在軌轉速遙測數據，處理得到衛星本體系中和慣性系中的角動量變化曲線如圖2 所示。

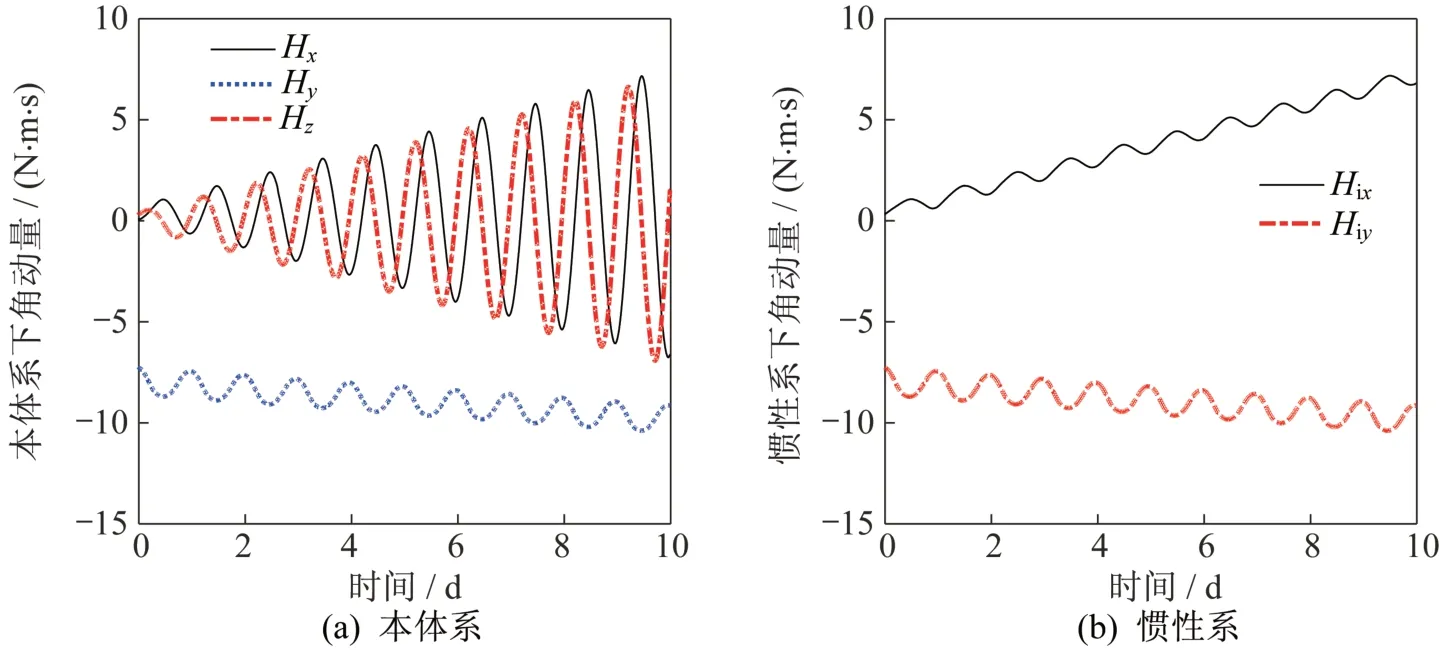
圖2 衛星在軌角動量變化示意圖Fig.2 Angular momentum change of the on-orbit satellite

對慣性系下的角動量曲線進行擬合，得到擬合結果如圖3 和圖4 所示。

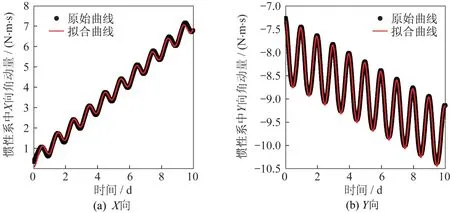
圖3 慣性系下整星角動量擬合結果Fig.3 Fitting results of the angular momentum of the whole satellite in the inertial frame

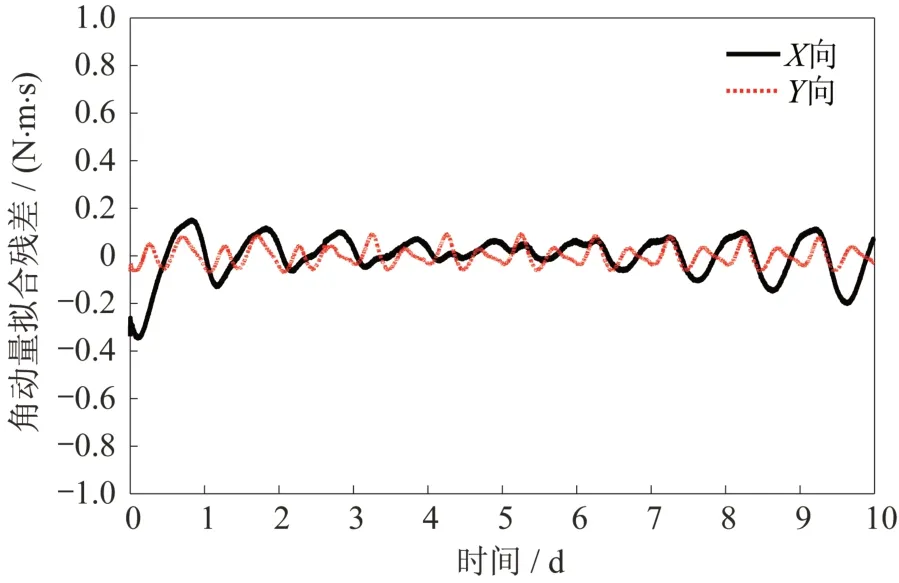
圖4 慣性系下整星角動量擬合殘差Fig.4 Fitting residual error of the whole satellite angular momentum in the inertial frame

對應特征參數的數值辨識結果如下：

已知衛星慣性角速度

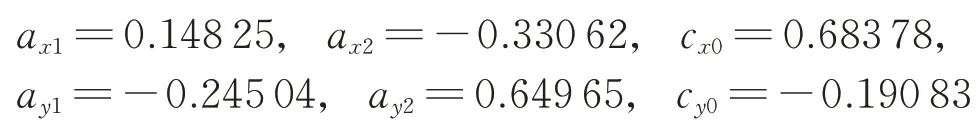
ω

=7.272 2×10rad/s，根據上述辨識結果可解得，在星下點時刻為12：00 對應的慣性參考系中：結果1，法向太陽光壓力引起的繞

O

X

軸干擾力矩，

P

?

F

=7.91×10N ?m；結果2，法向太陽光壓力引起的繞

O

Y

軸干擾力矩，

P

?

F

=3.54×10N ?m；結果3，切向太陽光壓力引起的繞

O

Z

軸干擾力矩，

P

?

F

=2.40×10N ?m；結果4，切向太陽光壓力引起的繞

O

X

軸干擾力矩，

P

?

F

=-2.24×10N ?m；結果5，繞

O

Y

軸重力梯度力矩，

T

=3

ω

?

I

=-2.20×10N ?m。

將上述辨識結果代入式（10），將仿真結果與在軌遙測結果比對，如圖5 所示，誤差在0.5 N·m·s 以內，表明所建角動量模型和特征參數辨識算法正確且有效。

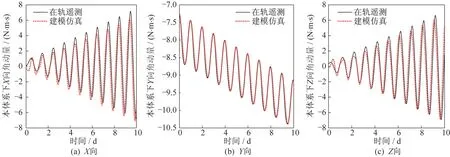
圖5 角動量仿真模型與在軌實際角動量比對示意圖Fig.5 Comparison diagram of the angular momentum simulation model and the actual on-orbit angular momentum

3 角動量管控

根據前文的角動量積累機理分析可知，為了延長GEO 衛星在軌的角動量卸載周期，一方面應盡量減小衛星質心與太陽光壓壓心之間的距離（尤其是在軌道法向）；另一方面應盡量減小衛星慣量積

I

，從而減小角動量積累的梯度。但是，隨著季節的變化和星上剩余燃料的減少，衛星的壓心、質心、轉動慣量和慣性積均不可避免發生變化。角動量管控的目的是為了延長卸載周期，根據角動量增長趨勢設置合理的角動量初值（即對應飛輪初始轉速）。因此，有必要對太陽光壓力矩和重力梯度力矩進行辨識，并根據辨識結果合理設置飛輪卸載轉速（而不是簡單卸載到零轉速），從而延長角動量卸載周期，提升衛星的在軌應用效能。假設衛星配置三正一斜總共4 臺飛輪，正裝

XYZ

飛輪與衛星本體軸一致，斜裝

S

飛輪與

XYZ

夾角一致，均為54.74°。以上一節的太陽光壓力矩和重力梯度力矩辨識結果為例，將其代入整星動力學模型，以飛輪轉速超過±2 000 r/min（對應角動量約15 N·m·s）為卸載標志，則可得不同飛輪組合接入狀態下，角動量管控前（對應飛輪初始轉速均為0 r/min）對應的卸載周期和進行角動量管控后的卸載周期見表2。由表2 可見，角動量管控后使得角動量卸載周期增加1 倍，管控前后的整星角動量累積曲線如圖6 和圖7 所示。圖7 中，從左到右4張圖分別展示了4 種接入工況下的飛輪轉速變化曲線，每張圖的最左側為設置的飛輪轉速初值，最右側為卸載時對應的飛輪轉速，橫坐標表示卸載周期。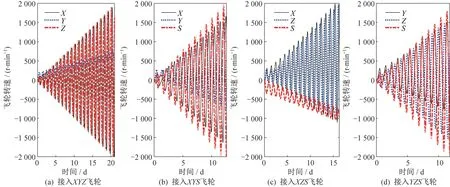

圖6 角動量管控前不同飛輪組合下的飛輪轉速變化仿真曲線Fig.6 Simulation curves of flywheel speed changes under different flywheel combinations before angular momentum management and control

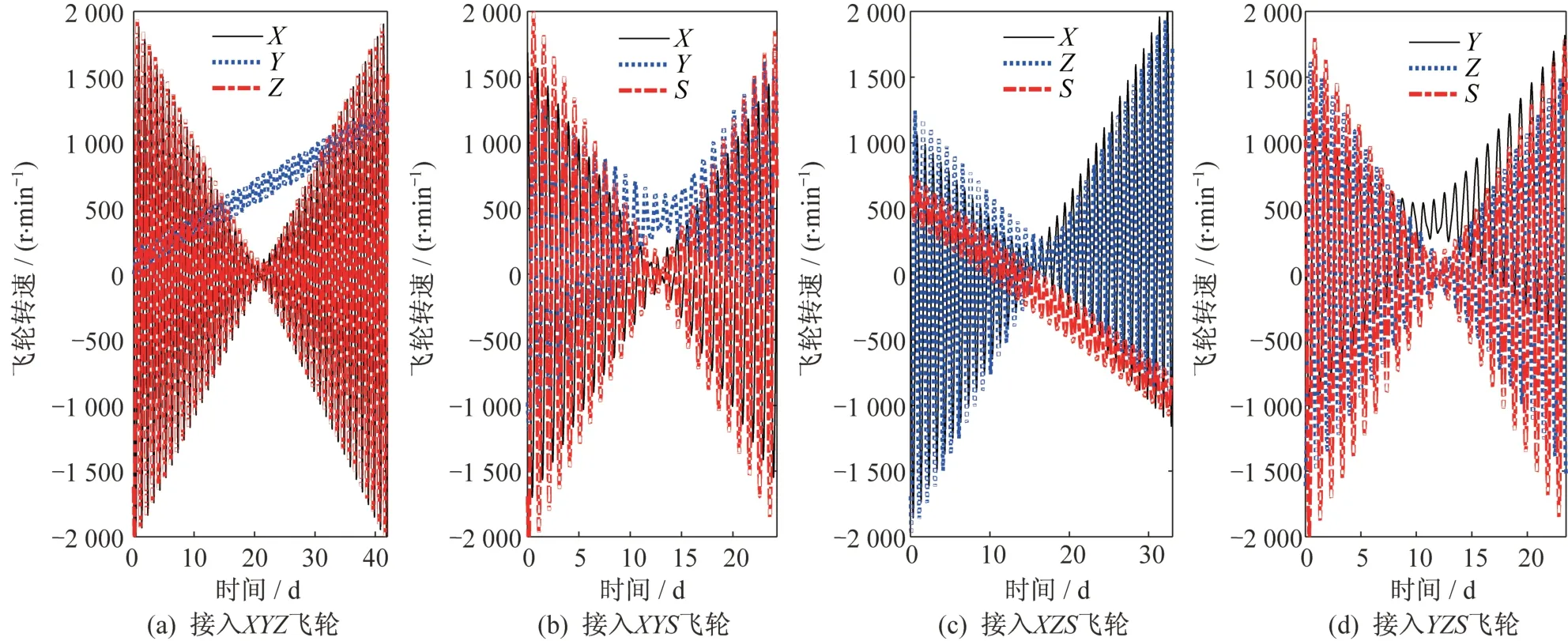
圖7 角動量管控后不同飛輪組合下的飛輪轉速變化仿真曲線Fig.7 Simulation curves of flywheel speed changes under different flywheel combinations after angular momentum management and control

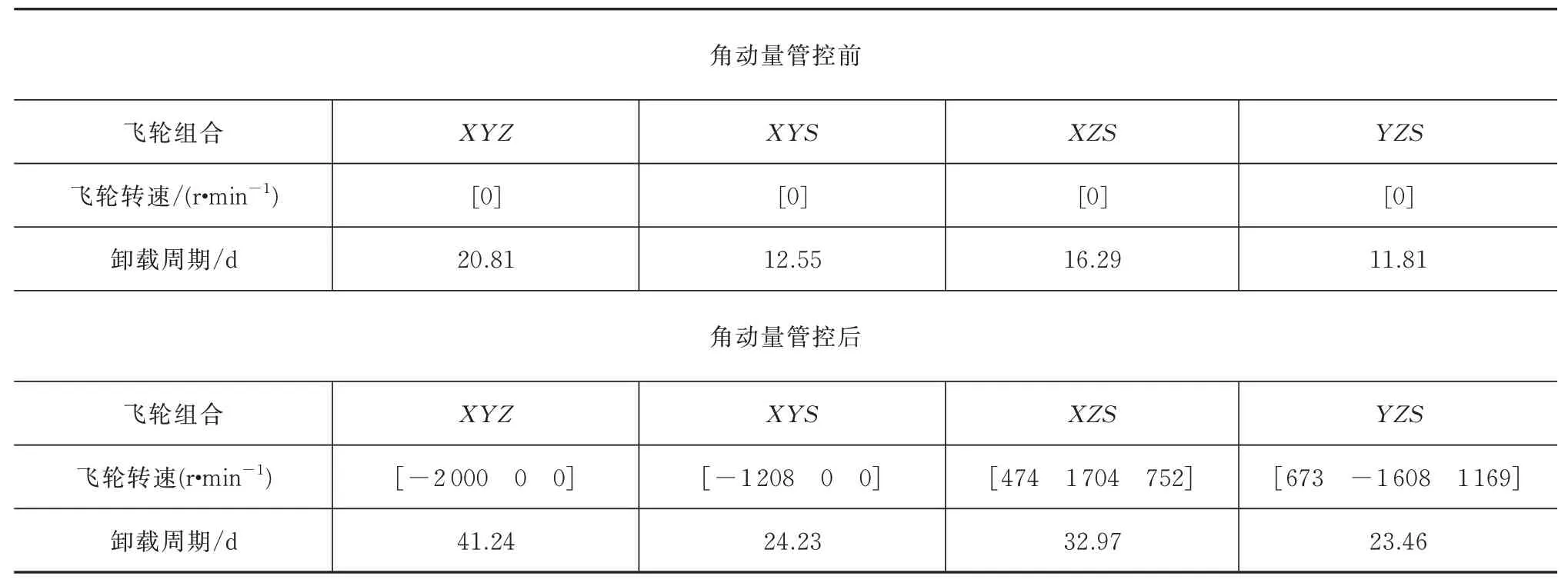
表2 不同飛輪組合下角動量管控前后卸載周期統計表Tab.2 Statistics of unloading periods before and after angular momentum management and control under different flywheel combinations

4 結束語

本文建立了慣性系下雙對稱太陽電池陣GEO衛星的角動量積累模型，并投影到衛星本體系中，將角動量積累轉化為實際飛輪轉速的變化。結合實際在軌飛輪轉速遙測數據，精準辨識GEO 衛星在軌環境干擾力矩，獲取定量結果，并作為輸入條件，仿真了不同飛輪組合接入狀態下的飛輪轉速變化情況。以角動量卸載周期最長為原則，優化了角動量管控策略，將飛輪的角動量卸載周期提升為原來的2 倍，大幅提升衛星在軌的應用效能。