星箭耦合力學(xué)分析中的衛(wèi)星混合模型研究

吳 松，秦 川，劉 松，趙玉震，郭其威，唐國安

（1.復(fù)旦大學(xué) 航空航天系，上海 200433；2.上海宇航系統(tǒng)工程研究所，上海 201109）

0 引言

為確保航天飛行器能安全可靠地運(yùn)行，航天飛行器結(jié)構(gòu)不僅要進(jìn)行靜態(tài)分析和靜力試驗(yàn)，還要進(jìn)行動力學(xué)分析與動態(tài)試驗(yàn)，必須采用以結(jié)構(gòu)動力學(xué)分析與試驗(yàn)為基礎(chǔ)的動態(tài)設(shè)計(jì)技術(shù)和動態(tài)優(yōu)化設(shè)計(jì)技術(shù)。為準(zhǔn)確預(yù)示衛(wèi)星所承受的載荷和動力學(xué)環(huán)境，需要衛(wèi)星研制單位提供代表衛(wèi)星動力學(xué)特性的數(shù)學(xué)模型給運(yùn)載火箭研制單位，形成運(yùn)載-衛(wèi)星系統(tǒng)級耦合動力學(xué)模型，進(jìn)行星箭耦合系統(tǒng)的動特性響應(yīng)分析，從而確定衛(wèi)星所承受的載荷及動力學(xué)響應(yīng)。

用于星箭耦合分析的衛(wèi)星模型通常以動態(tài)子結(jié)構(gòu)方法的縮聚形式提供，即將有限元物理模型內(nèi)部節(jié)點(diǎn)的剛度、質(zhì)量信息縮聚在邊界點(diǎn)上，采用有限元縮聚模型代替物理模型進(jìn)行力學(xué)分析，一方面可以避免輸出結(jié)構(gòu)設(shè)計(jì)的技術(shù)細(xì)節(jié)，起到技術(shù)保密的作用；另一方面可以大大減少模型本身的自由度，有利于提高力學(xué)分析的計(jì)算效率。長期以來，我國衛(wèi)星特點(diǎn)以“矮胖型”為主，以星箭界面載荷進(jìn)行結(jié)構(gòu)設(shè)計(jì)不會造成較嚴(yán)重的過試驗(yàn)。隨著航天任務(wù)需求的增加，多艙段結(jié)構(gòu)形式的衛(wèi)星逐步增多，單純以星箭界面載荷作為衛(wèi)星結(jié)構(gòu)設(shè)計(jì)的依據(jù)會帶來較嚴(yán)重的過設(shè)計(jì)，需要在星箭耦合分析時提取內(nèi)部界面的載荷。然而，由于衛(wèi)星方的動力學(xué)模型往往是單純的縮聚模型，無法直接提取內(nèi)部界面載荷，需要形成一種適應(yīng)內(nèi)部界面載荷提取的衛(wèi)星縮聚模型生成方法。

動態(tài)子結(jié)構(gòu)法是計(jì)算大型復(fù)雜結(jié)構(gòu)動態(tài)特性十分有效的方法，已被廣泛應(yīng)用于航空、航天、艦船、建筑、海洋工程、核工程，以及復(fù)雜機(jī)械結(jié)構(gòu)的設(shè)計(jì)與分析，例如運(yùn)載火箭的建模、星箭耦合分析、大型部件如航天相機(jī)、氦氣瓶等的建模、復(fù)合柔性結(jié)構(gòu)衛(wèi)星建模，以及衛(wèi)星的動力學(xué)分析。在星箭耦合分析研究方面，文獻(xiàn)［15］提出衛(wèi)星星箭耦合分析模型的二次縮聚方法，將由衛(wèi)星本體物理模型和天線一次縮聚模型組成的混合模型二次縮聚為滿足運(yùn)載格式的星箭耦合分析出口模型，并與火箭研制方聯(lián)合開展星箭耦合分析及結(jié)果校驗(yàn)，驗(yàn)證了該方法的有效性。文獻(xiàn)［10］介紹了采用約束邊界模態(tài)展開表達(dá)式進(jìn)行星/箭耦合響應(yīng)分析的方法，通過解析推導(dǎo)可以將整個星/箭耦合結(jié)構(gòu)多自由度方程減縮為僅含星/箭連接界面處自由度的方程，使動力學(xué)問題自由度數(shù)大大減縮。航天領(lǐng)域的動態(tài)子結(jié)構(gòu)方法研究主要集中在縮聚模型生成方法和自由度縮減方面，用于星箭耦合分析的衛(wèi)星混合模型研究則較少。

本文針對衛(wèi)星內(nèi)部界面載荷計(jì)算需求，將衛(wèi)星結(jié)構(gòu)進(jìn)一步拆分為多個子結(jié)構(gòu)；再基于動態(tài)子結(jié)構(gòu)的裝配規(guī)則，用物理單元將多個子結(jié)構(gòu)進(jìn)行組裝，形成用于耦合分析的衛(wèi)星混合模型。

1 衛(wèi)星混合模型生成的基本原理

1.1 衛(wèi)星子結(jié)構(gòu)劃分

假定衛(wèi)星需要輸出一個內(nèi)部界面載荷，其構(gòu)型如圖1 所示，將衛(wèi)星劃分2 個子結(jié)構(gòu)

a

、

b

。

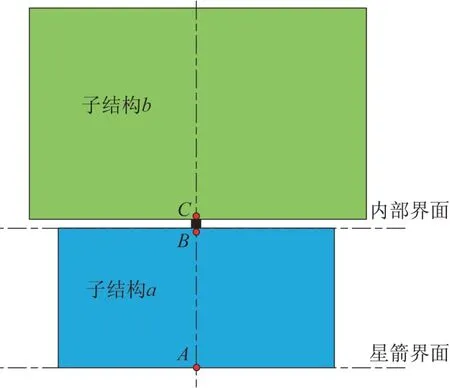
圖1 衛(wèi)星構(gòu)型示意圖Fig.1 Schematic diagram of satellite configuration

1.2 子結(jié)構(gòu)縮聚模型生成

對于子結(jié)構(gòu)系統(tǒng)，其振動方程為

定義子結(jié)構(gòu)的外部物理節(jié)點(diǎn)，計(jì)算其主模態(tài)和約束模態(tài)為

式中：

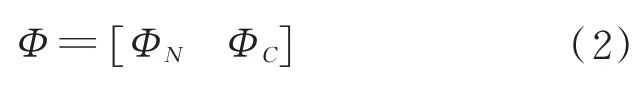
Φ

為結(jié)構(gòu)的主模態(tài)集，即固定界面模態(tài)，

Φ

=[

Φ

… 0]；

Φ

為結(jié)構(gòu)的約束模態(tài)集，

Φ

=[

Φ

…

I

]。

將子結(jié)構(gòu)系統(tǒng)的物理坐標(biāo)采用模態(tài)坐標(biāo)進(jìn)行表示：

式中：

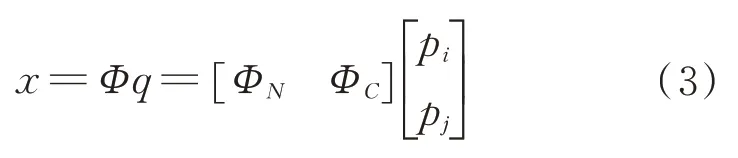
p

為對應(yīng)主模態(tài)的模態(tài)坐標(biāo)；

p

為對應(yīng)約束模態(tài)的模態(tài)坐標(biāo)。利用式（3）將子結(jié)構(gòu)振動方程變換到模態(tài)坐標(biāo)

p

上，得到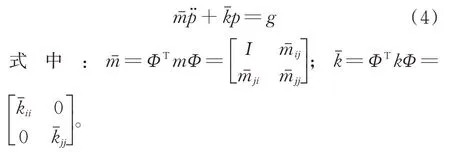

因此，若子結(jié)構(gòu)

a

的外部節(jié)點(diǎn)為

A

點(diǎn)和

B

點(diǎn)，則子結(jié)構(gòu)

a

縮聚模型對應(yīng)的質(zhì)量陣和剛度陣分別為

式中：下標(biāo)1 為子結(jié)構(gòu)

a

與運(yùn)載火箭連接界面自由度；下標(biāo)2 為子結(jié)構(gòu)

a

與子結(jié)構(gòu)

b

連接界面自由度；

q

為子結(jié)構(gòu)

a

縮聚模型的廣義坐標(biāo)。若將子結(jié)構(gòu)

b

的

C

點(diǎn)定義為外部節(jié)點(diǎn)，則子結(jié)構(gòu)

b

截?cái)嗪蟮馁|(zhì)量陣和剛度陣為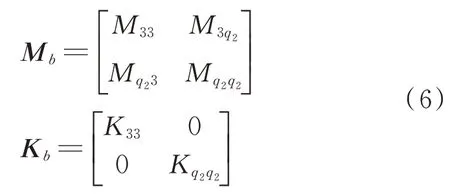

式中：下標(biāo)3 為子結(jié)構(gòu)

b

與子結(jié)構(gòu)

a

連接界面自由度；

q

為子結(jié)構(gòu)

b

縮聚模型的廣義坐標(biāo)。

1.3 子結(jié)構(gòu)間的連接剛度

子結(jié)構(gòu)

a

、

b

之間的界面連接剛度可等效為6 個方向的剛度，記為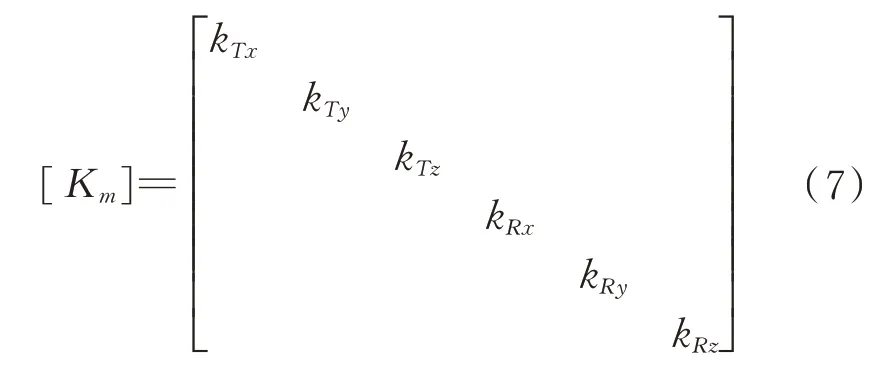

則子結(jié)構(gòu)

a

、

b

連接界面的剛度矩陣為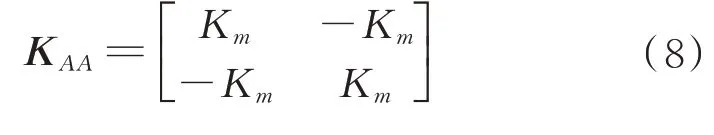

1.4 子結(jié)構(gòu)裝配

若不考慮子結(jié)構(gòu)

a

、

b

間連接剛度時，對子結(jié)構(gòu)

a

、

b

進(jìn)行組裝，則衛(wèi)星綜合后質(zhì)量陣和剛度陣分別為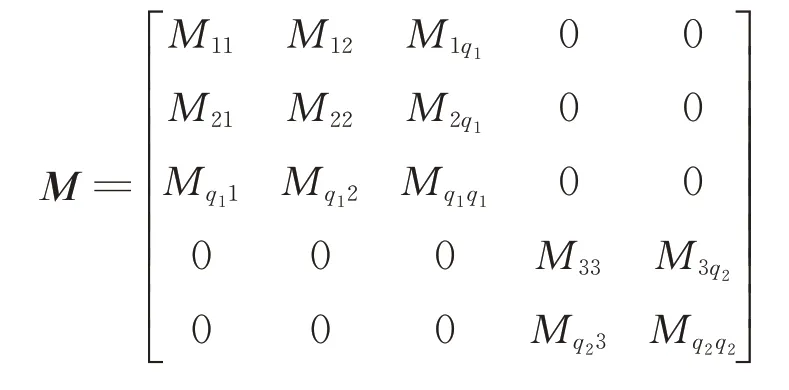

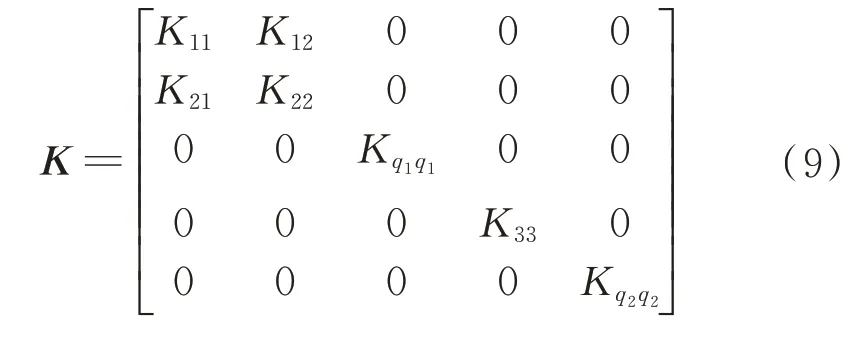
若計(jì)及子結(jié)構(gòu)

a

和子結(jié)構(gòu)

b

間的連接剛度時，衛(wèi)星綜合后的剛度矩陣為

在建立衛(wèi)星有限元模型時，子結(jié)構(gòu)間的連接剛度可采用彈簧單元或梁單元進(jìn)行建模。因此，在定義好各子結(jié)構(gòu)的外部節(jié)點(diǎn)后，可首先按照動態(tài)子結(jié)構(gòu)縮聚理論分別生成各子結(jié)構(gòu)的縮聚模型，再依據(jù)各子結(jié)構(gòu)間的連接剛度，按照上述裝配關(guān)系，組裝生成用于星箭耦合分析的衛(wèi)星混合模型。

該模型中，各子結(jié)構(gòu)的動態(tài)特性采用縮聚形式表示，子結(jié)構(gòu)間的連接剛度采用物理模型表示，星箭耦合分析時，可直接輸出該物理單元的載荷等響應(yīng)信息。

2 數(shù)值算例

以如圖2 所示的包含2 個艙段的典型衛(wèi)星結(jié)構(gòu)為例，由于其結(jié)構(gòu)呈現(xiàn)出“細(xì)長型”的特點(diǎn)，需要進(jìn)一步分解衛(wèi)星內(nèi)部界面載荷等信息，降低衛(wèi)星“過設(shè)計(jì)”程度，提升衛(wèi)星的有效載荷比。

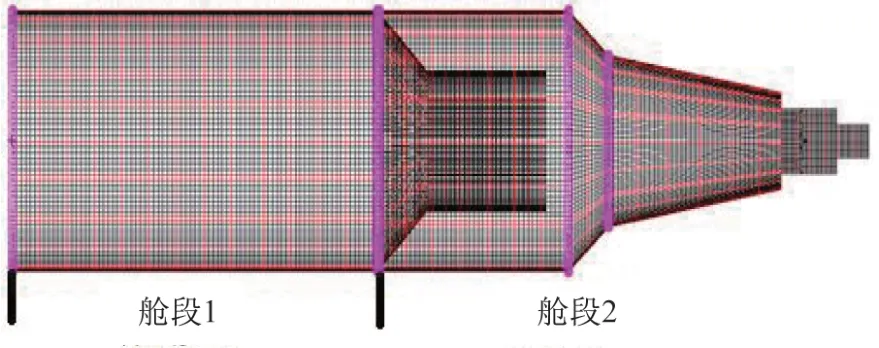
圖2 實(shí)驗(yàn)艙總體構(gòu)型Fig.2 Overall configuration of the experimental cabin

衛(wèi)星總長約20 m，發(fā)射質(zhì)量達(dá)22 t，包含艙段1、艙段2。艙段1 質(zhì)量約13 t，艙段2 質(zhì)量約9 t。其中，艙段1 與試驗(yàn)夾具、艙段2 之間通過多個螺栓法蘭結(jié)構(gòu)進(jìn)行緊固連接，某一側(cè)連接法蘭的局部詳細(xì)結(jié)構(gòu)如圖3 所示。

圖3 艙段間的連接法蘭Fig.3 Connecting flanges between compartments

建立衛(wèi)星的有限元分析模型，依據(jù)衛(wèi)星的結(jié)構(gòu)特點(diǎn)，將其劃分為子結(jié)構(gòu)

a

、

b

，2 個子結(jié)構(gòu)間的連接形式通常為螺栓法蘭連接結(jié)構(gòu)，考慮到實(shí)際工程中往往僅關(guān)心界面間的總載荷，而不關(guān)心局部連接點(diǎn)的載荷，因而可將各子結(jié)構(gòu)連接界面的點(diǎn)采用多點(diǎn)約束剛性連接至中心點(diǎn)，衛(wèi)星原始物理模型中，子結(jié)構(gòu)間采用一維彈簧單元或梁單元進(jìn)行連接，最終劃分的子結(jié)構(gòu)如圖4 所示。

A

、

B

點(diǎn)為子結(jié)構(gòu)

a

的外部節(jié)點(diǎn)，其中，

A

點(diǎn)為衛(wèi)星與運(yùn)載連接的界面點(diǎn)；

B

點(diǎn)為子結(jié)構(gòu)

a

上與子結(jié)構(gòu)

b

的連接界面點(diǎn)；

C

點(diǎn)為子結(jié)構(gòu)

b

的外部節(jié)點(diǎn)，即子結(jié)構(gòu)

b

上，與子結(jié)構(gòu)

a

的連接界面點(diǎn)。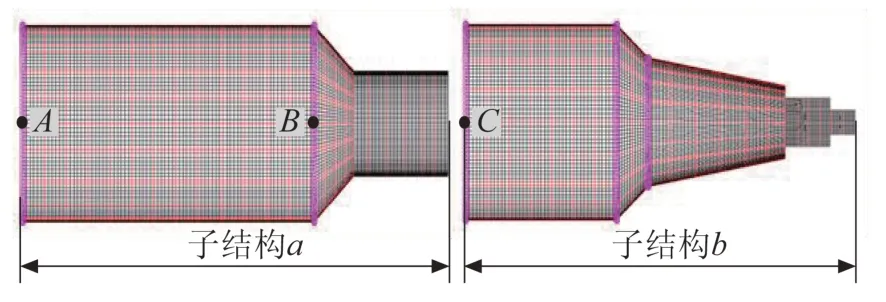

圖4 衛(wèi)星子結(jié)構(gòu)劃分Fig.4 Satellite substructure division

依次生成子結(jié)構(gòu)

a

、

b

的廣義剛度矩陣和廣義質(zhì)量矩陣，保留子結(jié)構(gòu)

a

、

b

之間的一維單元，依據(jù)式（10）進(jìn)行組裝，形成縮聚后的衛(wèi)星混合模型。該模型包含衛(wèi)星整體的質(zhì)量陣和剛度陣，依據(jù)該質(zhì)量陣和剛度陣求解其廣義特征值，得到混合模型下衛(wèi)星的模態(tài)頻率。子結(jié)構(gòu)

a、b

保留不同模態(tài)階數(shù)時，混合模型下衛(wèi)星的模態(tài)頻率計(jì)算結(jié)果見表1。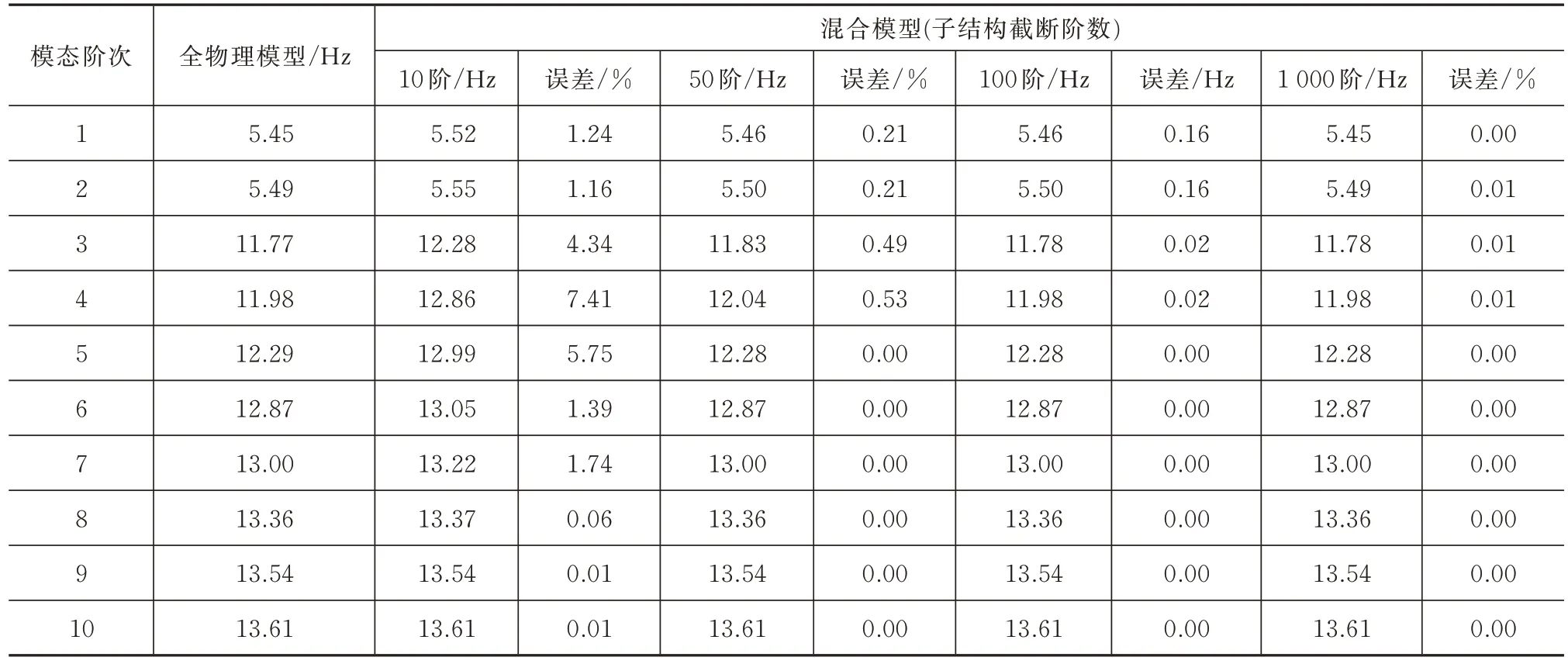

表1 衛(wèi)星混合模型的計(jì)算精度Tab.1 Calculation accuracy of the satellite hybrid model

由表1 可知，子結(jié)構(gòu)在保留較少階次的模態(tài)信息時，即可保證衛(wèi)星混合模型與全物理有限元模型的計(jì)算結(jié)果基本一致，說明混合模型能夠滿足星箭耦合分析的計(jì)算精度。而用于星箭耦合分析的衛(wèi)星模型截?cái)嗤ǔＴ?00 階以上，故衛(wèi)星的混合模型不會降低星箭耦合分析的精度。此外，表中第5～10 階頻率為子結(jié)構(gòu)局部頻率，表明混合模型的精度與子結(jié)構(gòu)的模態(tài)截?cái)嚯A次影響不大。

3 結(jié)束語

以某典型衛(wèi)星結(jié)構(gòu)為例，對“細(xì)長型”衛(wèi)星在星箭耦合分析中其內(nèi)部界面載荷的計(jì)算需求問題，基于子結(jié)構(gòu)縮聚及裝配的基本原理，提出了用于星箭耦合分析的衛(wèi)星混合模型生成方法。該方法在保留了縮聚模型各項(xiàng)優(yōu)點(diǎn)的基礎(chǔ)上，可實(shí)現(xiàn)內(nèi)部界面物理單元的載荷輸出，滿足工程計(jì)算精度的需求，在星箭耦合分析時獲取更多響應(yīng)信息，為衛(wèi)星設(shè)計(jì)提供指導(dǎo)。