用于改善直流鏈電流紋波的電流源型整流器扇區優化調制策略

肖蕙蕙 周琛力 郭 強 李 山 周青青

用于改善直流鏈電流紋波的電流源型整流器扇區優化調制策略

肖蕙蕙 周琛力 郭 強 李 山 周青青

（重慶理工大學重慶市能源互聯網工程技術研究中心 重慶 400054）

電流源型整流器采用十二扇區空間矢量脈寬調制（SVPWM）可縮短器件換流過程并減小開關損耗，但整流器在運行時直流鏈電流紋波較大，而采用增大電感值的方法抑制電流紋波會增大電感的損耗和體積，影響系統整體運行性能。為此，該文首先提出一種適用于寬范圍運行情況下直流鏈電流紋波的優化調制策略。其次，基于十二扇區實現機理和電感電流紋波產生原理，通過所提出的電流紋波分析模型推導分析電流紋波表達式，并深入對比分析兩種調制策略的直流鏈電流紋波峰值分布規律。最后，通過仿真和實驗樣機驗證了理論分析的正確性和調制策略的有效性。

電流源型整流器 優化調制 直流鏈電流紋波 十二扇區

0 引言

脈寬調制（Pulse Width Modulating, PWM）變流器運行在整流模式時，根據其直流鏈儲能形式的不同可分為電壓源型整流器（Voltage Source Rectifier, VSR）和電流源型整流器（Current Source Rectifier, CSR）[1-2]。目前，VSR仍是研究的重點，但在大多數應用場合VSR需要兩級功率變換，從而增加了系統的體積和成本。而CSR因其結構簡單，可實現單級降壓整流并有寬范圍輸出電壓調節能力和易于并聯運行、直流短路時可靠性高等優點，受到了工業界和學術界的關注。CSR可應用于高壓直流數據中心供電系統[3-4]、大功率電動汽車直流充電系統[5-6]、飛機動力分配系統[7-8]以及可再生能源系 統[9-10]等領域。

整流器運行時，其性能除受到硬件水平和控制策略的影響，還與系統調制策略有關。目前，變流器常采用空間矢量脈寬調制（Space Vector PWM, SVPWM），為六扇區電流矢量調制。在此基礎上，若將扇區進行細分并調整開關矢量序列，可縮短器件換流過程，從而在不改變整流器開關頻率情況下，提高系統效率和運行性能[11-13]。

直流鏈電感電流紋波作為CSR重要性能指標之一，與系統調制策略緊密相關。較大的電感電流紋波不僅降低系統效率，同時還會引起網側電流總諧波畸變率（Total Harmonic Distortion, THD）增加。針對該問題，常采取增大電感值對電流紋波進行抑制，但這將增加系統的體積和成本。因此，研究CSR調制策略來改善電流紋波對提高系統性能具有重要意義。不同SVPWM策略的差異在于各矢量切換序列，其中以零矢量分配為主。文獻[14]對不同空間矢量調制進行對比研究，為變流器調制策略的選用提供了理論依據。文獻[15]針對三相三開關Buck- Boost變換器研究了不同調制方案對電感電流紋波的影響，通過對零矢量的分配來減小直流鏈電流紋波。文獻[16]提出了一種適用于電流源型變換器的不對稱十二扇區優化開關矢量序列，在較高調制比下可有效減小直流鏈電流紋波。文獻[17-18]根據伏秒平衡原理調整橋臂直通時間，從而減小Z源變換器電感電流紋波。文獻[19]針對三相雙Buck變換器，提出采用占空比補償的控制方法逐漸降低電感電流紋波，并改善電流過零畸變。文獻[20]提出一種用于模塊化多電平變換器的廣義離散模型和模型預測方法來抑制不平衡條件下直流鏈電流紋波。文獻[21]針對間接矩陣變換器提出一種優化調制策略改善輸出電壓波形質量。文獻[22]提出電流紋波預測方法，實現開關頻率可變的電流紋波抑制。

目前，電流源型變換器在采用十二扇區調制（Twelve Sector Modulation, TSM）時，存在實現過程不完整和直流鏈電流紋波較大等問題。為此本文首先，從扇區判斷、選取開關矢量序列和計算各矢量占空比等方面推導分析TSM策略的實現過程；其次，提出了一種等效直流鏈電流紋波分析模型，從電感電流紋波產生原理上對CSR的電流紋波進行詳細分析并推導出電流紋波峰值表達式；然后，根據TSM策略的開關序列與電流紋波關系，提出一種在0～1全調制比范圍內改善CSR直流鏈電流紋波的優化扇區調制（Optimized Sector Modulation, OSM）策略，且深入對比分析兩種調制策略的直流鏈電流紋波峰值大小；最后，通過仿真和實驗樣機對所提出策略進行驗證。

1 直流鏈電流紋波分析模型

1.1 拓撲結構

三相CSR主拓撲如圖1所示，圖中，a、b、c為三相電網電壓，a、b、c為三相并網電流，網側二階ss濾波器用來濾除高頻開關分量，d為無源阻尼電阻，直流鏈接dc平滑輸出電流，L為輸出電容，開關管S1～S6采用IGBT串聯二極管結構，可以提供器件反向阻斷能力，同時輸出側并聯續流二極管VD，可以簡化邏輯、降低導通損耗。

圖1 三相CSR主拓撲

1.2 分析模型

根據CSR降壓特性和空間矢量調制原理，本文提出一種等效直流鏈電流紋波分析模型，如圖2所示。其中，[S, S]（,=1, 2,…,6）為電流空間矢量對應的開關組合，pn為橋臂電壓。

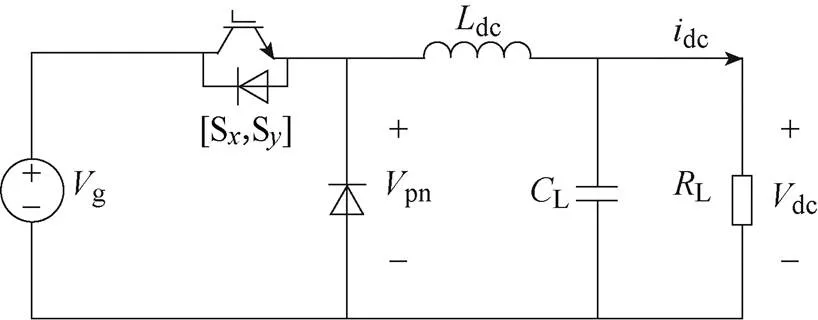
圖2 直流鏈電流紋波等效分析模型

由圖2可知，電流源型整流器可以等效為Buck模型，開關管導通時，g為整流器導通開關管對應兩相之間的線電壓，且在每個開關周期內為瞬時直流電壓。g在不同開關組合下表達式為

根據輸入功率和輸出功率相等原則，輸出直流電壓平均值表達式為

式中，為電壓調制比；m為電網電壓基波峰值。

在不同開關組合下，橋臂電壓pn呈現脈沖序列形式。根據伏秒平衡原理，其平均值與輸出直流電壓平均值相等，但在每個開關周期中，脈沖電壓與輸出平均電壓并不相等，且兩者產生的電壓差值將在電感上產生近似線性化的電流紋波。因此，直流鏈電流紋波可通過電感電流變化率d/d進行有效分析，通過分析整流器模型，由基爾霍夫電壓定律得到整流器電感電流紋波表達式為

式中，為開關管占空比；s為開關頻率。

根據式（3）可知，當直流電感和開關頻率確定時，直流鏈電流紋波與橋臂電壓和輸出平均電壓的電壓差值以及開關管占空比有關。其中橋臂電壓為脈沖序列形式，與瞬時直流電壓g有關，而g對應不同開關組合即電流空間矢量序列。從而可以根據電流空間矢量序列和開關管占空比推導分析整流器直流鏈電流紋波大小。

2 直流鏈電流紋波分析

2.1 十二扇區SVPWM

傳統SVPWM策略分為6個扇區，在其基礎上，可進一步將一個電網工頻周期均勻劃分為12個扇區，電網電壓與扇區分布如圖3所示。每個扇區內電網相電壓有確定的大小關系。例如，在扇區1內，有a＞0＞b＞c，以此作為扇區判斷依據。

圖3 電網電壓與扇區分布

十二扇區劃分如圖4所示，根據系統調制比的不同，指令電流矢量*的大小和位置可以利用6個非零矢量1～6和3個零矢量7～9進行合成。

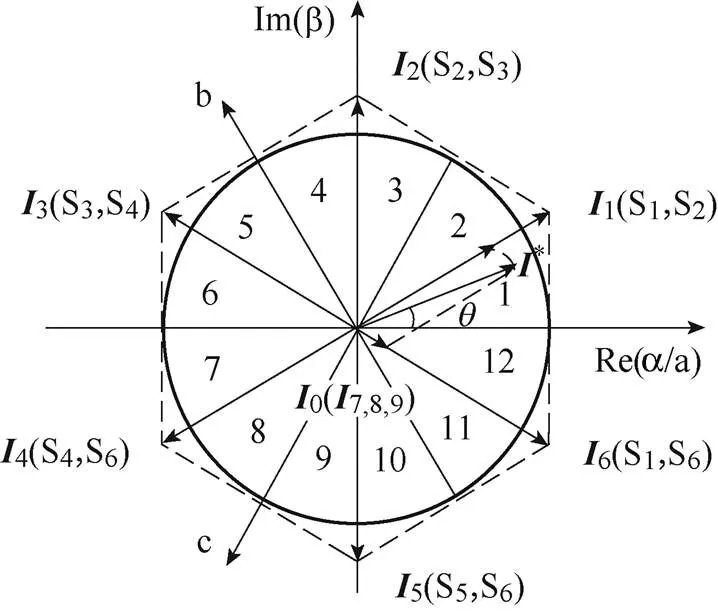
圖4 十二扇區劃分

為保證良好的輸出性能，采用雙邊對稱電流矢量序列，每個扇區矢量序列使得對稱調制方案中平均開關電壓最低，且能夠明顯縮短器件之間的換流過程[11-12]，各扇區電流空間矢量序列見表1。

表1 各扇區電流空間矢量序列

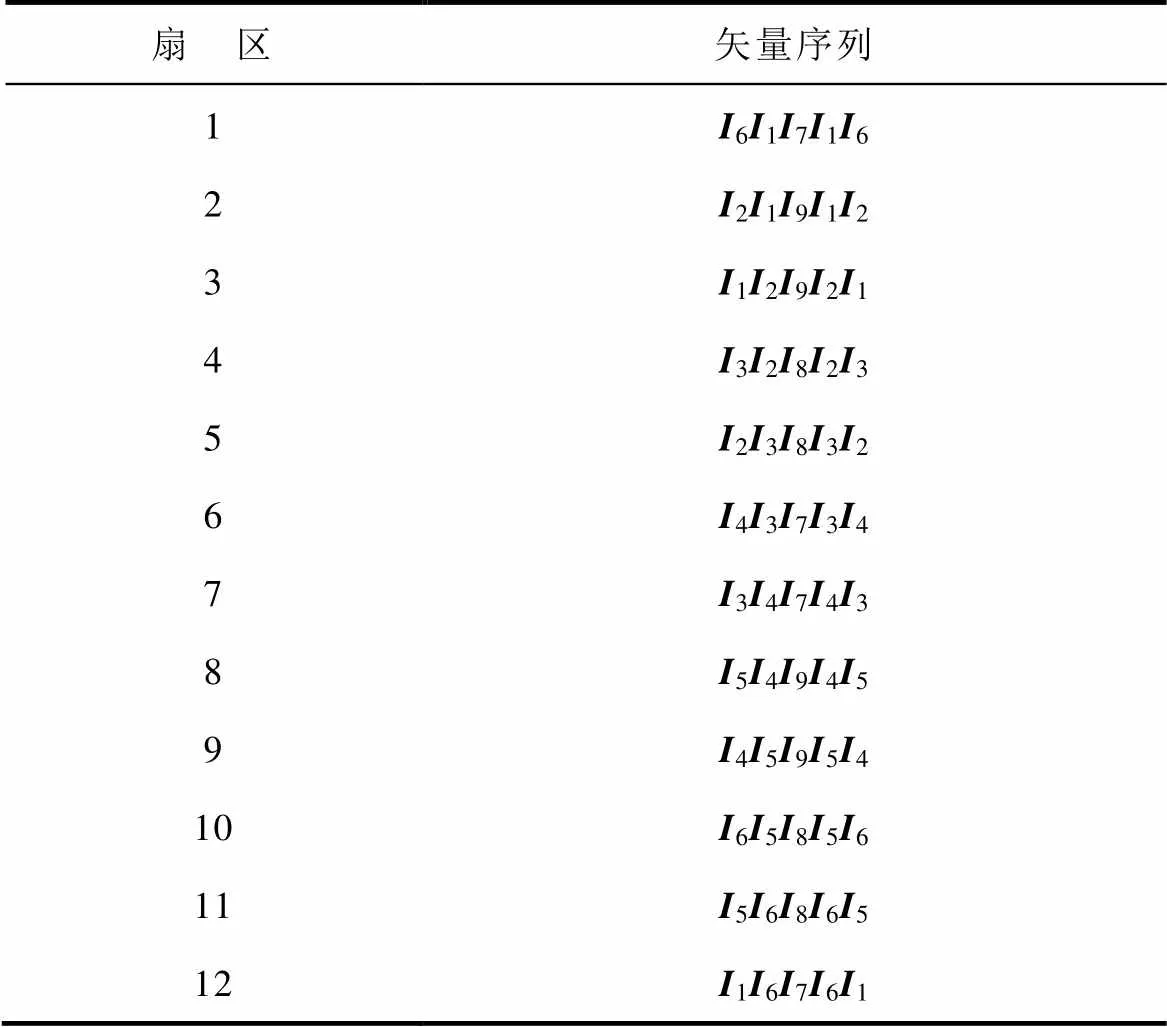
Tab.1 Current space vector sequence of each sector

定義調制比函數為

當指令電流位于扇區12內時，利用1、6和7合成指令電流矢量，根據安秒平衡原理和式（4），電流矢量占空比表達式為

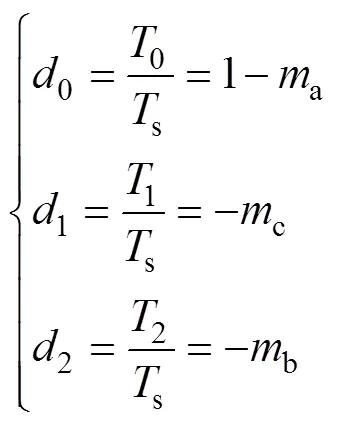
式中，1、2和0分別為矢量1、6和7的導通時間；1、2和0分別為1、6和7的占空比；s為開關周期。

同理，當指令電流位于其余各扇區內時，可分別推導出電流矢量占空比表達式，見表2。

表2 各扇區電流空間矢量占空比

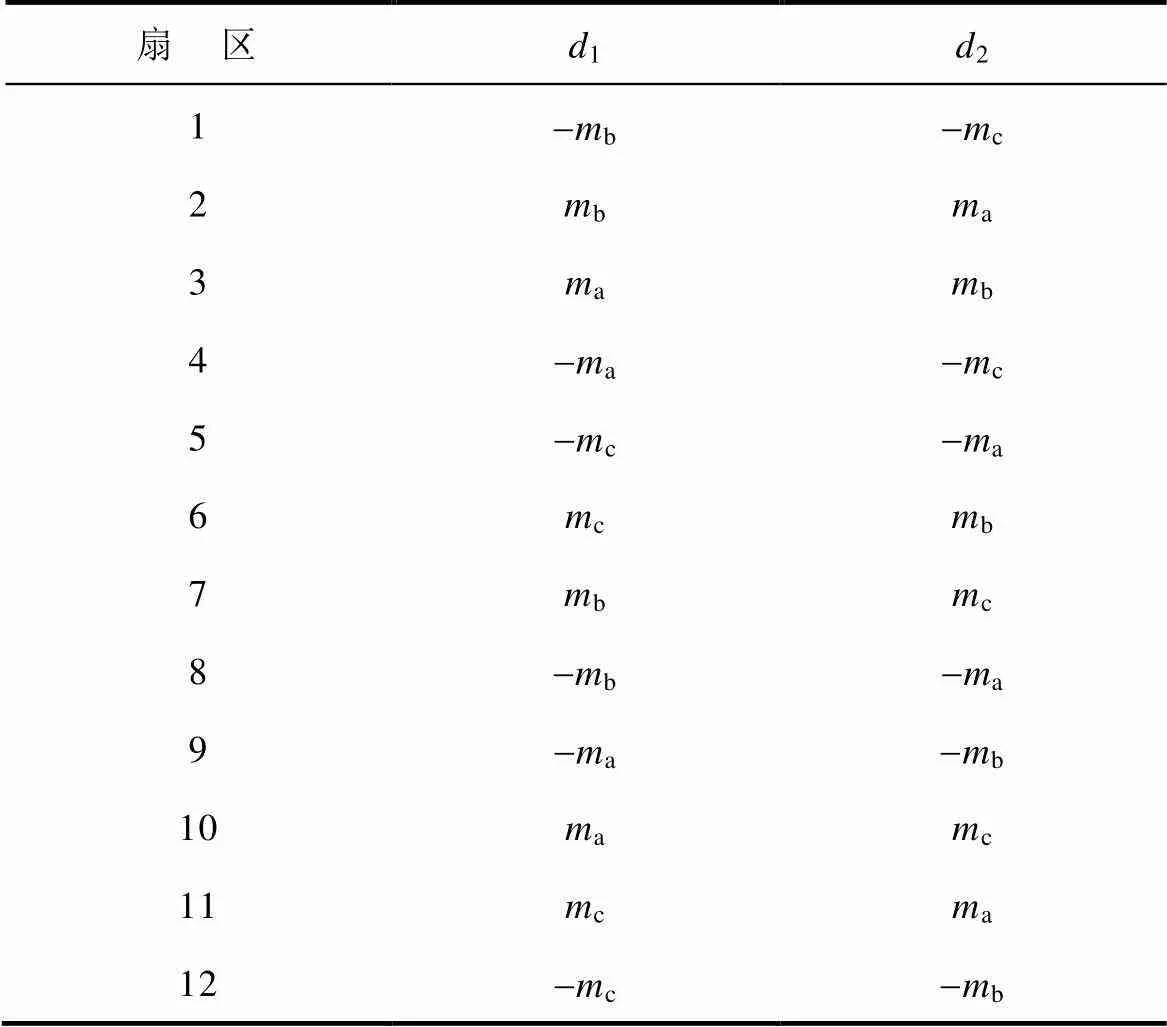
Tab.2 Duty cycle of each sector current space vector

2.2 電感電流紋波分析

當指令電流位于扇區12內和扇區1內時，采用本文提出的等效分析模型，得到CSR等效電路模型，如圖5所示。隨著電流空間矢量序列切換，模型的開關狀態不斷變化。

根據式（3），矢量1作用時，圖5中開關置于2，有g=ac，直流鏈電感電流紋波峰值為

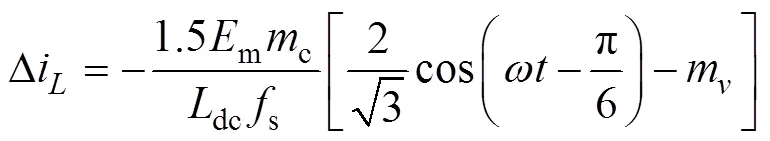
圖5 扇區12和扇區1下的等效模型

Fig.5 Equivalent model of sector 12 and sector 1

矢量6作用時，圖5中開關置于1，有g=ab，直流鏈電感電流紋波峰值為

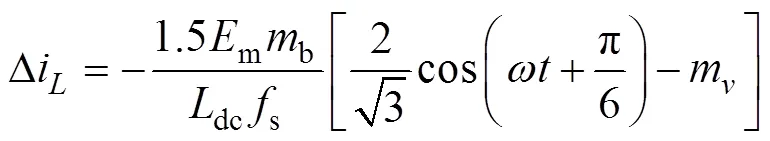
矢量7作用時，圖5中開關置于3，有g=0，直流鏈電感電流紋波峰值為

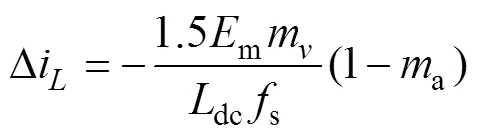
由式（6）～式（8）可知，在參數m、dc和s確定情況下，整流器直流鏈電流紋波與調制比函數以及扇區角（指令電流旋轉角度t）有關。

將作用在扇區12和扇區1內的瞬時直流電壓按開關周期和各矢量占空比進行劃分，得到扇區12和扇區1的開關脈沖序列，如圖6所示。

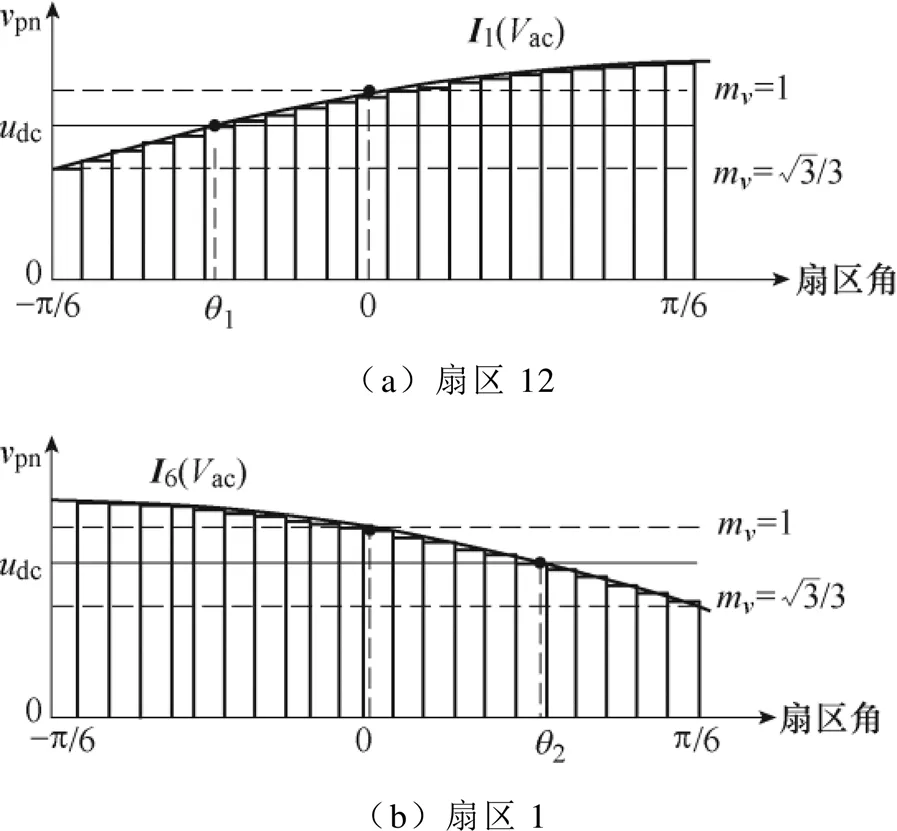
圖6 扇區內開關脈沖序列劃分

從圖6可知，根據瞬時直流電壓的取值范圍和輸出平均電壓大小可以確定在不同調制范圍內脈沖電壓與輸出平均電壓關系。以扇區12的一個開關周期脈沖序列為例，如圖7所示。

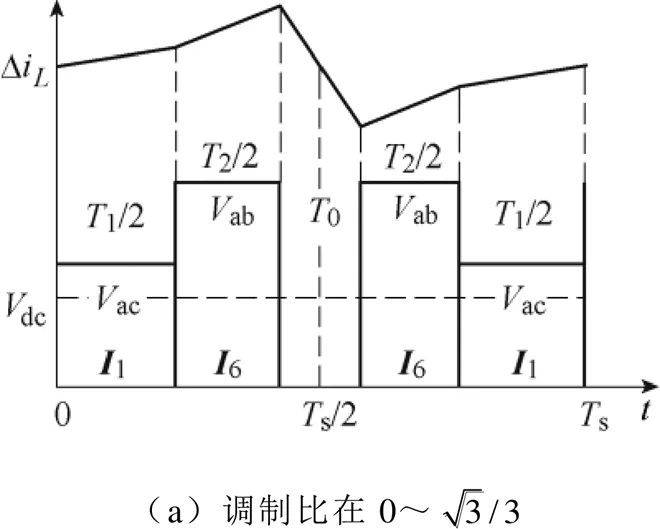
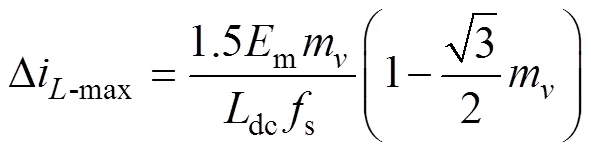
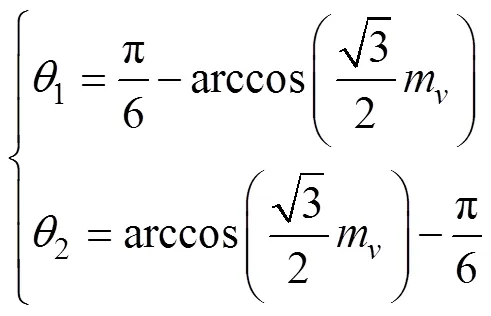
當-p/6＜＜1或2＜＜p/6時，輸出平均電壓幅值介于兩個脈沖電壓幅值之間，此時直流鏈電流紋波最大峰值為

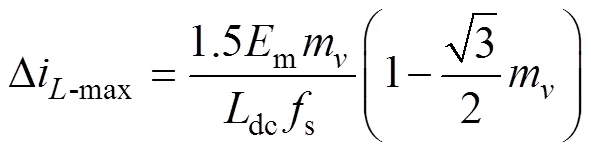
當1＜＜2時，輸出平均電壓幅值始終小于脈沖電壓幅值，此時紋波取決于扇區角，當t=1時，其電流紋波最大峰值為

（12）

通過表達式（9）～式（12）可以看出，當系統調制比在0～1范圍變化時，采用TSM策略得到電流紋波峰值為零矢量作用時的電流紋波峰值，并與t有關。兩扇區中電流紋波分析如圖8所示，在扇區12內，紋波峰值隨增加而減小，而在扇區1內則相反，電流紋波最大峰值分布在兩個扇區的兩側。

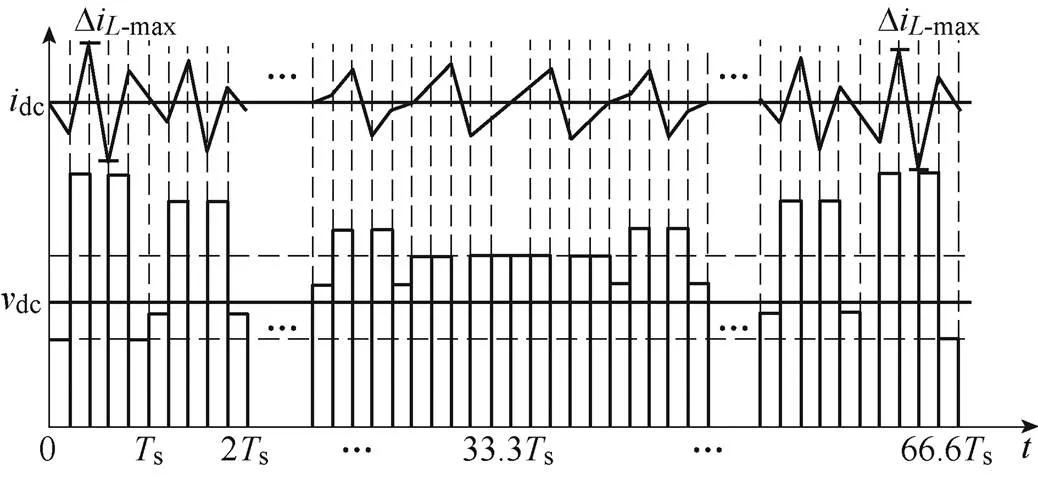
圖8 兩扇區中電流紋波分析

根據本文提出的等效分析模型，繪制出調制比為0～1，扇區12、扇區1中的CSR直流鏈電流紋波峰值，如圖9所示。

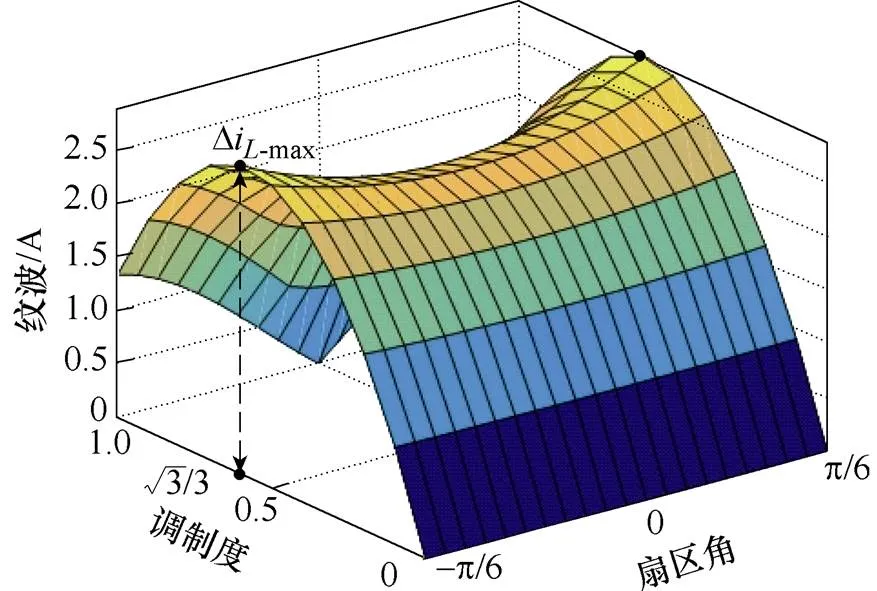
圖9 兩扇區中直流鏈電流紋波

3 優化調制策略

傳統空間矢量調制常采用兩個相鄰非零矢量和一個零矢量合成指令電流矢量。每個扇區非零矢量對應不同瞬時直流電壓。以扇區12和扇區1為例，兩扇區的瞬時直流電壓波形如圖10所示。

由圖10可知，扇區12和扇區1均采用非零矢量6、1和零矢量7以合成指令電流矢量。實際上，在扇區12和扇區1內，有效非零矢量除6、1外，還包括5和2。其中5在扇區12內有效，2在扇區1內有效。在此基礎上，每個扇區內可利用3個有效非零矢量合成指令電流。

根據上述分析，對TSM策略的開關脈沖序列進行改進，以扇區12內的一個開關周期脈沖序列為例展開分析，改進的開關脈沖序列如圖11所示。

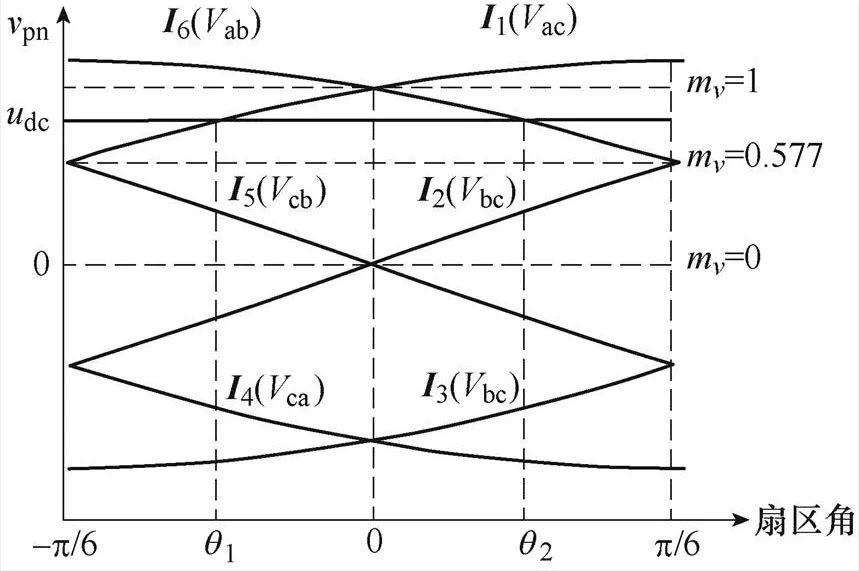
圖10 兩扇區的瞬時直流電壓波形

由圖11可知，改進方式Ⅰ采用3個有效非零矢量6、1和5合成指令電流矢量，即在TSM策略基礎上，將零矢量7替換為非零矢量5，在5矢量作用期間，cb(c-b)能夠減小脈沖電壓與輸出平均電壓差值，使得直流鏈電流紋波降低，如圖12所示。不難看出，CSR直流鏈電流紋波峰值隨著調制比增加而逐漸減小。

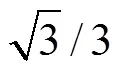
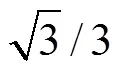
圖12 改進方式I直流鏈電流紋波

圖13 改進方式Ⅱ直流鏈電流紋波

圖14 OSM策略下直流鏈電流紋波

由圖14可知，采用OSM策略后，CSR在寬輸出范圍內能夠有效降低直流鏈電流紋波峰值。電流紋波最大峰值從兩個扇區兩側變化到兩個扇區同一側，即圖14中扇區角 =0處。這是由于在扇區12內，cb隨著扇區角的增加而減小，從而脈沖電壓與輸出平均電壓的電壓差值逐漸增大，而扇區1則相反。當扇區角 =0時，兩種調制策略下直流鏈電流紋波峰值一致，但OSM策略下為最大紋波峰值，而TSM策略下為最小紋波峰值。

圖15給出了CSR在TSM、OSM兩種調制策略下直流鏈電流紋波最大峰值。其中，TSM策略的扇區角為-p/6、p/6，OSM策略的扇區角在0附近，經比較可以看出，采用OSM策略，CSR直流鏈電感電流紋波最大峰值明顯小于十二扇區調制。

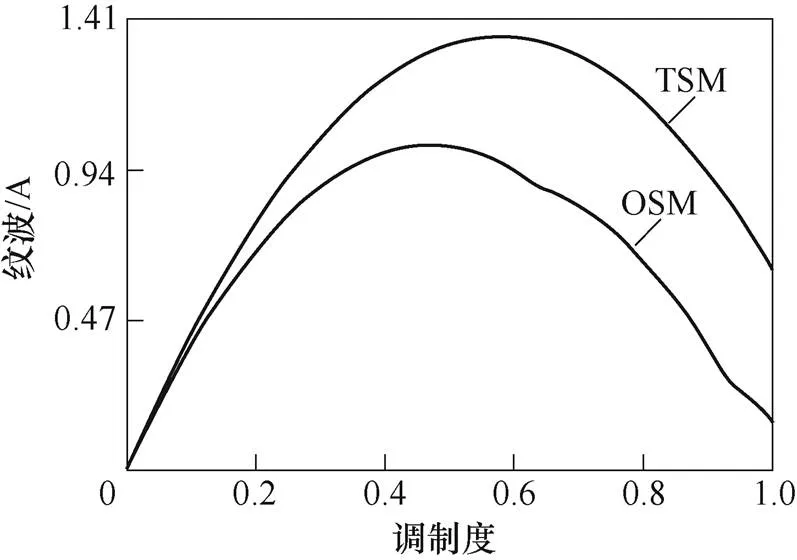
圖15 TSM、OSM最大紋波峰值對比

4 仿真驗證

為驗證所提出調制策略和等效分析模型的正確性，利用Matlab/Simulink搭建系統仿真模型，其仿真參數見表3。

表3 仿真參數

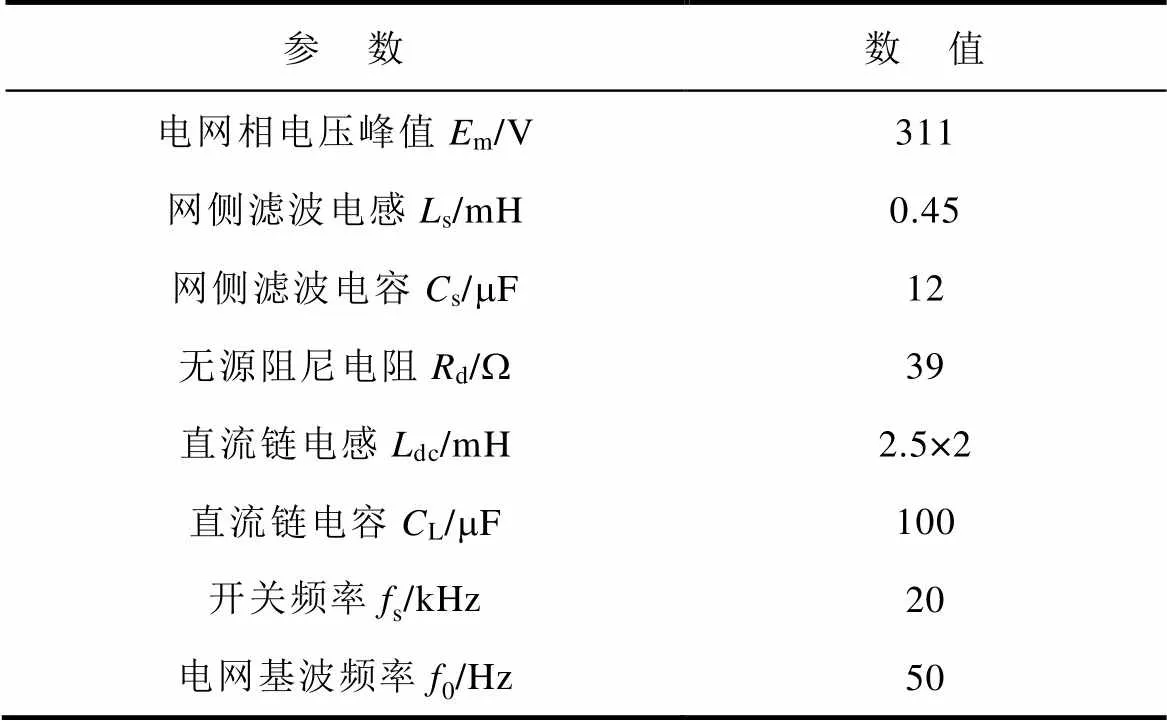
Tab.3 Simulation parameters

圖16為CSR在TSM策略下的直流鏈電流紋波與脈沖電壓仿真波形。可以看出，在調制比較高情況下，零矢量作用時間較短，由于每個開關周期內脈沖電壓差異，直流鏈電流紋波峰值呈現中間小兩側大的分布趨勢。而在調制比較低情況下，零矢量作用時間較長，電流紋波較大且分布均勻，仿真結果與文中分析一致。

分別對兩種調制比下采用TSM策略的網側電流進行快速傅里葉變換（Fast Fourier Transform, FFT）分析，TSM策略下的a相電網電流的頻譜分析如圖17所示。

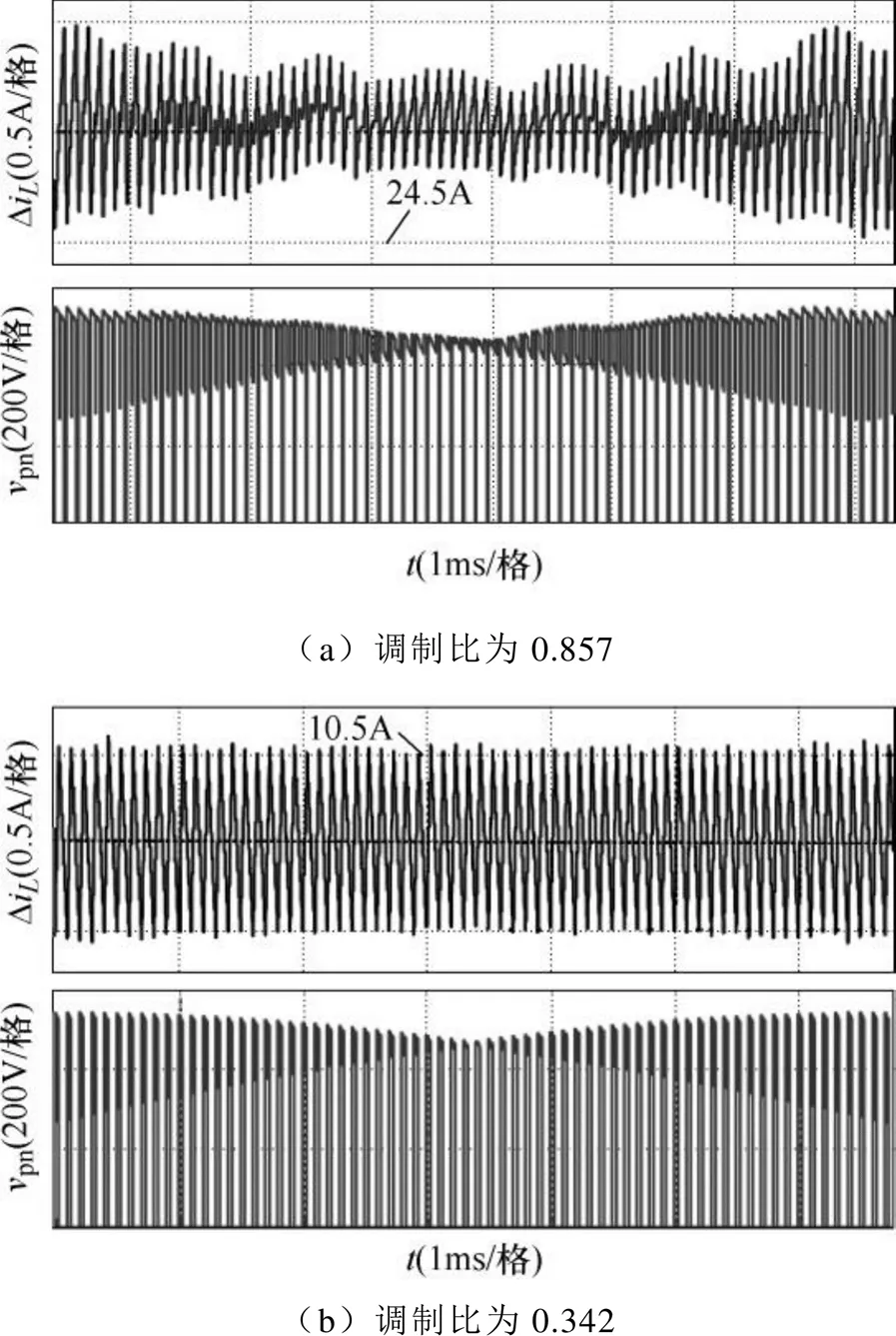
圖16 TSM策略下的直流鏈電流紋波與脈沖電壓仿真波形

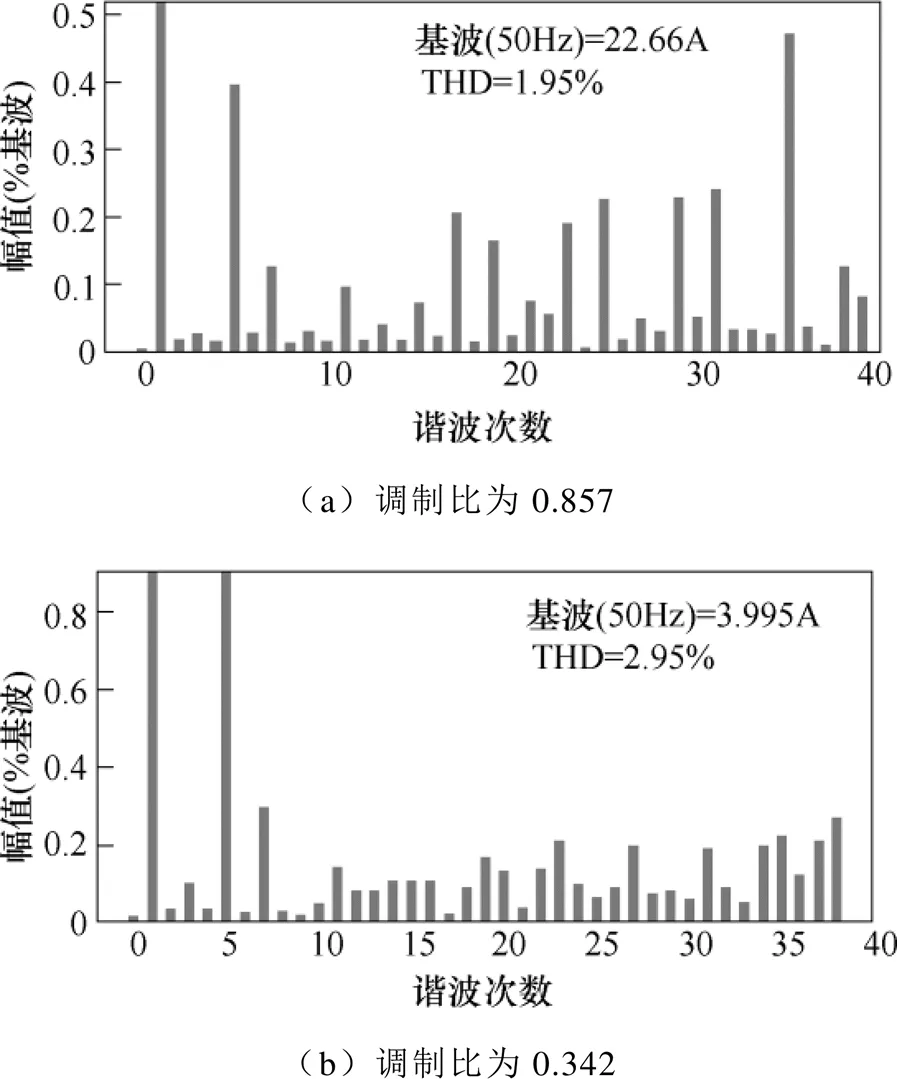
圖17 TSM策略下的a相電網電流的頻譜分析

由圖17可知，系統在較低調制比下，電網電流THD要高于在較高調制比下的THD，但兩種調制比下均能夠滿足IEEE-519標準，驗證了TSM策略的可行性。

采用OSM策略得到的仿真波形如圖18所示，經與圖16對比，可以看出，CSR在OSM策略下的直流鏈電流紋波不論是較高調制比還是較低調制比都明顯優于TSM策略，且電流紋波峰值分布較為均勻，表明本文所提出的OSM策略能夠有效改善直流鏈電流紋波。

圖18 OSM策略下的直流鏈電流紋波與脈沖電壓仿真波形

分別對兩種調制比下采用OSM策略的網側電流進行FFT分析，如圖19所示。不難看出，在相同工況條件下，采用OSM策略，其網側電流THD要高于TSM策略，在低調制比下則更加顯著，其THD將大于5%，但在較高調制比下，系統THD滿足IEEE-519標準。

由于采用間隔2p/3的兩非零矢量和零矢量合成指令電流矢量，且CSR在TSM策略下PWM脈沖分布不規則，使得網側輸入電流在扇區交界處出現電流畸變，如圖20所示。在扇區8向扇區9過渡時，出現開關S4占空比增大，S1和S6占空比丟失的現象，從而使得脈沖電壓ca作用時長增加，同時ab作用時長減小，最終導致輸入電流a、b發生畸變。

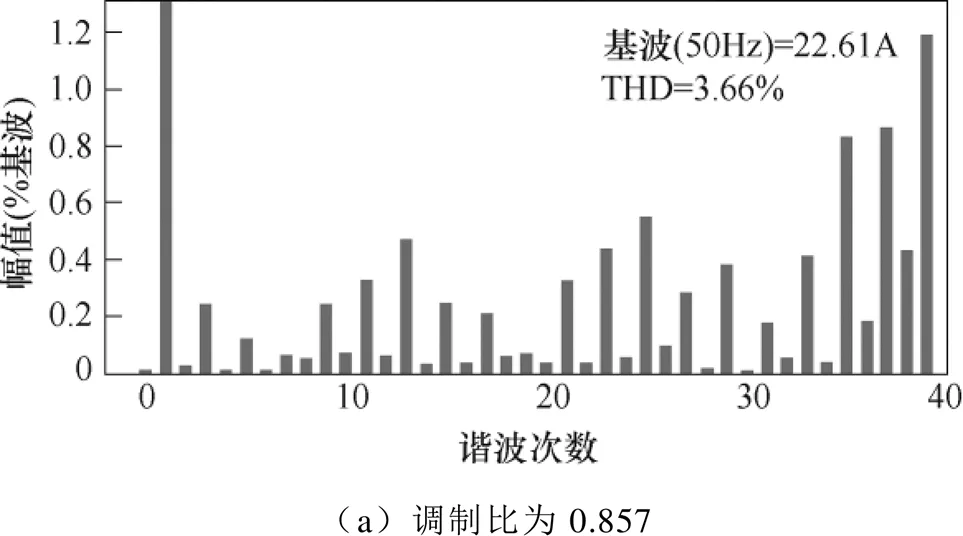
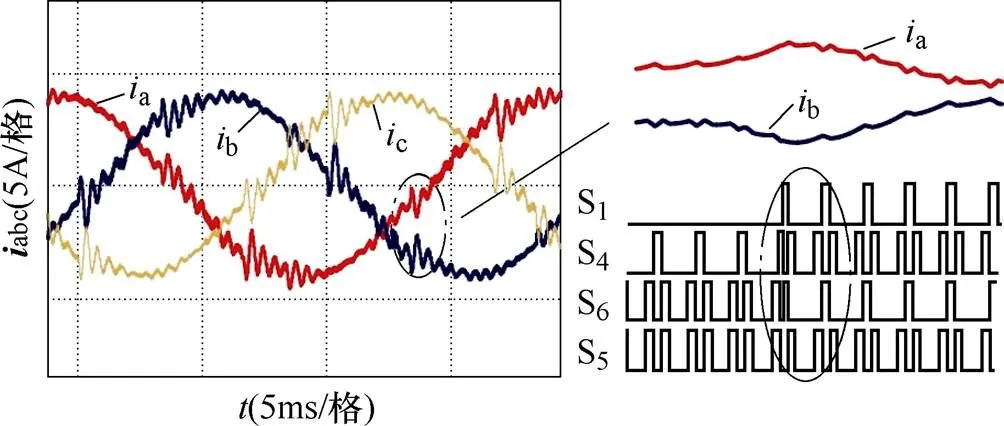
圖20 扇區交界處網側電流畸變

在低調制比下，零矢量作用時間較長，扇區交界處輸入電流畸變被放大，使得網側電流THD增大。為了有效抑制畸變，可采用在扇區交界附近調整占空比或提高系統開關頻率等方法[23-25]。

5 實驗結果

針對三相CSR拓撲結構，搭建了一臺10kW實驗樣機進行實驗驗證，如圖21所示。其中，控制主板芯片為TI TMSF28335 DSP和Xilinx XC95288 CPLD，主電路功率開關管和串聯二極管分別采用Infineon FF100R12RT4和IXY MEA75-12DA，電壓和電流傳感器分別采用LEM LV25-P和LEM HAS50- S，軟件部分采用基于模型的設計，如圖22所示，將Simulink模型轉換為系統控制代碼，實現代碼自動生成及運行，實驗參數同仿真參數一致。

圖23為CSR在TSM下的直流鏈電流紋波與脈沖電壓實驗波形。在兩種調制比下，直流鏈電感電流紋波最大峰值分別為1.6A和1.7A，實驗結果與仿真分析一致。

圖21 三相CSR實驗平臺

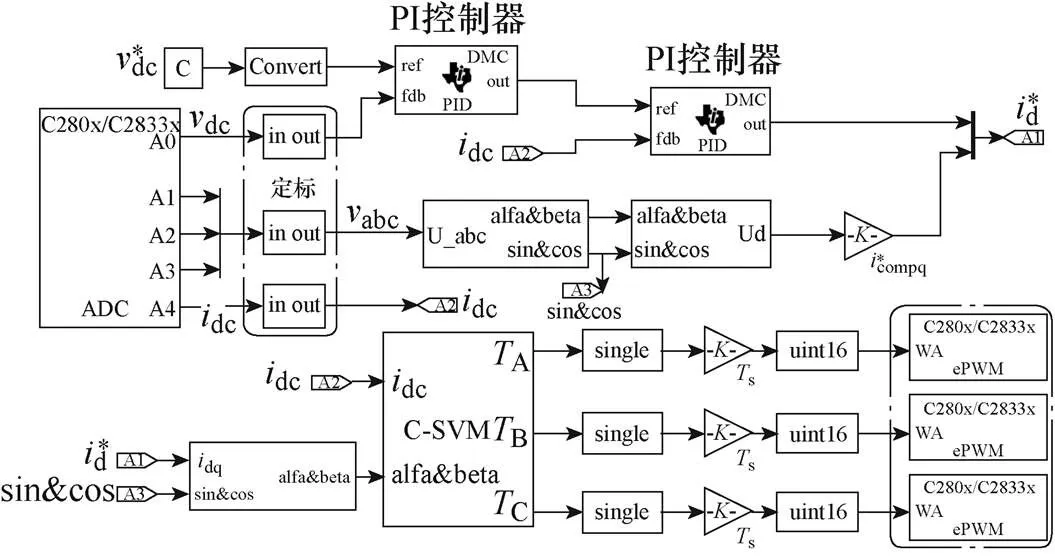
圖22 控制算法快速實現的Simulink模型

圖23 TSM策略下的直流鏈電流紋波與脈沖電壓實驗波形

圖24為OSM策略下的直流鏈電流紋波與脈沖電壓實驗波形。在兩種調制比下，直流鏈電感電流紋波最大峰值分別為1.1A和1.3A，對比TSM實驗結果，直流鏈電流紋波有明顯減小，這與仿真分析一致。

圖25為本文提出調制方案在穩態運行時網側電流、電壓及直流鏈電流、電壓波形。實驗結果表明在低調制比下，OSM策略因扇區過渡造成輸入電流畸變，這與圖20分析一致，需采用占空比補償等方法進行抑制。此外所提出調制方案能夠使系統在穩態運行時電網電壓與網側電流保持同相位，直流鏈電壓、電流能夠追蹤給定值，且直流鏈電流紋波得到顯著改善。

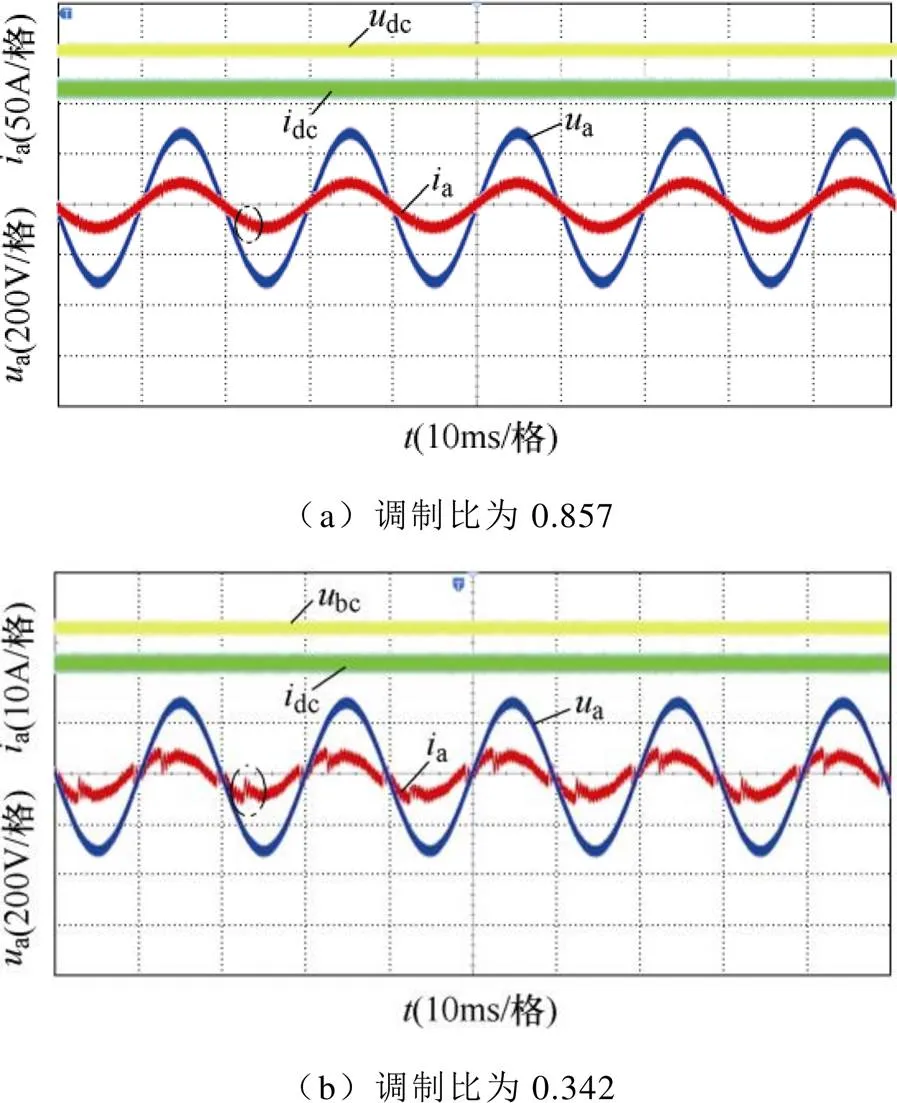
圖25 CSR穩態運行實驗結果

6 結論

針對三相CSR采用空間矢量調制對直流鏈電流紋波的影響，本文詳細分析了TSM策略實現過程，通過提出一種等效直流鏈電流紋波分析模型詳實推導整流器直流鏈電流紋波表達式，并量化分析調制策略與直流鏈電流紋波關系。在此基礎上提出一種十二扇區優化調制策略（OSM策略）并進行理論分析。通過仿真與實驗驗證，得到結論如下：

1）TSM策略在縮短器件換流過程基礎上，CSR直流鏈電流紋波峰值較大且紋波峰值為零矢量作用時的電感電流紋波峰值。

2）在不增加開關頻率和硬件的情況下，采用OSM調制方案，能有效減小十二扇區零矢量作用期間電流紋波峰值，并改善全調制比范圍內CSR直流鏈電流紋波。

3）在較低調制比下OSM會加劇十二扇區在扇區交界處引起的輸入電流畸變，可采用占空比補償等方法進行抑制。

[1] 郭強, 劉和平, 彭東林, 等. 電流型PWM整流器多環控制策略及其參數設計[J]. 中國電機工程學報, 2015, 35(5): 1193-1202.

Guo Qiang, Liu Heping, Peng Donglin, et al. Multi loop control strategy and parameter design of current source PWM rectifier[J]. Proceedings of the CSEE, 2015, 35(5): 1193-1202.

[2] 張崇巍, 張興. PWM整流器及其控制[M]. 北京: 機械工業出版社, 2003.

[3] Xu Fan, Guo Ben, Tolbert L M, et al. An all-SiC three-phase Buck rectifier for high-efficiency data center power supplies[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2662-2673.

[4] Xu Fan, Guo Ben, Xu Zhuxian, et al. Paralleled three- phase current-source rectifiers for high-efficiency power supply applications[J]. IEEE Transactions on Industry Applications, 2015, 51(3): 2388-2397.

[5] Saber C, Labrousse D, Revol B, et al. Challenges facing PFC of a single-phase on-board charger for electric vehicles based on a current source active rectifier input stage[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6192-6202.

[6] 郭強, 劉和平, 彭東林, 等. 一種考慮電池自身特性的電流源型充電系統[J]. 電工技術學報, 2016, 31(16): 16-25.

Guo Qiang, Liu Heping, Peng Donglin, et al. A current-source charging system considering the characteristics of battery[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 16-25.

[7] Zhao Sisi, Molina J M, Silva M, et al. Design of energy control method for three-phase Buck-type rectifier with very demanding load steps to achieve smooth input currents[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 3217-3226.

[8] Singh A K, Jeyasankar E, Das P, et al. A matrix- based nonisolated three-phase AC-DC rectifier with large step-down voltage gain[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4796-4811.

[9] Wei Qiang, Wu Bin, Xu Dewei, et al. A new configuration using PWM current source converters in low-voltage turbine-based wind energy conversion systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(2): 919-929.

[10] Wei Qiang, Wu Bin, Xu Dewei, et al. A medium- frequency transformer-based wind energy conversion system used for current-source converter-based offshore wind farm[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 248-259.

[11] Baumann M, Nussbaumer T, Kolar J W. Comparative evaluation of modulation methods of a three-phase Buck+Boost PWM rectifier. part I: theoretical analysis[J]. IET Power Electronics, 2008, 1(2): 255-267.

[12] Nussbaumer T, Baumann M, Kolar J W. Comparative evaluation of modulation methods of a three-phase Buck+Boost PWM rectifier. part II: experimental veri- fication[J]. IET Power Electronics, 2008, 1(2): 268- 274.

[13] 黃守道, 趙禮, 鄭劍, 等. 基于扇區細分六相電壓源逆變器全調制范圍的空間矢量脈寬調制方法[J]. 電工技術學報, 2019, 34(24): 5070-5083.

Huang Shoudao, Zhao Li, Zheng Jian, et al. Space vector pulse width modulation strategy for six-phase voltage source inverter in full modulation range based on sector subdivision method[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5070-5083.

[14] 蔣先強, 武奕彤, 何金奎, 等. 不同空間矢量調制下三相兩電平并網變換器的差模電流與共模電壓對比研究[J]. 電工技術學報, 2019, 34(增刊2): 586- 595.

Jiang Xianqiang, Wu Yitong, He Jinkui, et al. Research on differential-mode current and common- mode voltage of three-phase two-level grid-connected converters under different space vector modulation[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 586-595.

[15] Baumann M, Kolar J W. Minimization of the DC current ripple of a three-phase Buck-Boost PWM unity power factor rectifier[C]//Proceedings of the Power Conversion Conference-Osaka, Osaka, Japan, 2002: 472-477.

[16] 郭小強, 楊勇, 王學惠. 電流源變換器直流鏈電流紋波抑制策略研究[J]. 中國電機工程學報, 2018, 38(20): 6071-6078.

Guo Xiaoqiang, Yang Yong, Wang Xuehui. Optimal space vector modulation of current-source converter for DC-link current ripple reduction[J]. Proceedings of the CSEE, 2018, 38(20): 6071-6078.

[17] He Yuyao, Xu Yuhao, Chen Jinping. New space vector modulation strategies to reduce inductor current ripple of Z-source inverter[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(3): 2643-2654.

[18] Iijima R, Isobe T, Tadano H. Optimized short- through time distribution for inductor current ripple reduction in Z-source inverters using space-vector modulation[J]. IEEE Transactions on Industry Appli- cations, 2019, 55(3): 2922-2930.

[19] 陸依然, 肖嵐, 王勤, 等. 基于占空比補償的三相雙Buck并網逆變器電流過零畸變控制策略[J]. 電工技術學報, 2018, 33(12): 2841-2849.

Lu Yiran, Xiao Lan, Wang Qin, et al. Current zero crossing distortion control strategy for three-phase dual Buck grid-connected inverter based on duty cycle compensation[J]. Transactions of China Elec- trotechnical Society, 2018, 33(12): 2841-2849.

[20] Dekka A, Wu B, Zargari N R. Minimization of DC- bus current ripple in modular multilevel converter under unbalanced conditions[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4125-4131.

[21] 孫盼, 孫軍, 吳旭升, 等. 間接矩陣變換器優化SVPWM及其簡化的同步控制[J]. 電工技術學報, 2019, 34(10): 2187-2193.

Sun Pan, Sun Jun, Wu Xusheng, et al. Optimized space vector pulse width modulation and simplified synchronization control of indirect matrix converter[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2187-2193.

[22] Jiang Dong, Wang Fei. Variable switching frequency PWM for three-phase converters based on current ripple prediction[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4951-4961.

[23] Guo Ben, Wang Fei, Burgos R, et al. Modulation scheme analysis for high-efficiency three-phase Buck-type rectifier considering different device com- binations[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 4750-4761.

[24] Guo Ben, Xu Fan, Zhang Zheyu, et al. Compensation of input current distortion in three-phase Buck rectifiers[C]//2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, 2013: 930-938.

[25] 王濤, 陳昌松, 段善旭, 等. 用于改善電流過零點畸變的Vienna整流器空間矢量調制策略[J]. 電工技術學報, 2019, 34(18): 3854-3864.

Wang Tao, Chen Changsong, Duan Shanxu, et al. An improved space-vector modulation for Vienna rectifier to eliminating current distortion around zero-crossing point[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3854-3864.

Optimized Sector Modulation Strategy of Current Source Rectifier for DC-Link Current Ripple Reduction

（Chongqing Energy Internet Engineering Technology Research Center Chongqing University of Technology Chongqing 400054 China）

Twelve sector space vector pulse width modulation (SVPWM) can shorten the commutation process and reduce the switching loss of current source rectifier. However, the DC link current ripple is large when the rectifier is in operation. The DC link current ripple can be reduced by increasing the inductance, but the inductance loss and size will increase accordingly, affecting the overall operation performance of the system. Therefore, this paper proposes an optimized modulation strategy for DC link current ripple in wide range operation. Secondly, based on the twelve-sector implementation mechanism and inductor current ripple generation principle, the current ripple expression is deduced and analyzed through the proposed current ripple analysis model, and the peak distribution of DC link current ripple of the two modulation strategies is compared and analyzed. Finally, the theoretical analysis and the effectiveness of the proposed method are verified through simulation and experimental prototype.

Current source rectifier, optimized modulation, DC link current ripple, twelve sectors

10.19595/j.cnki.1000-6753.tces.201008

TM461

重慶市教委科學技術研究計劃項目（KJQN202001128）和重慶市教委科學技術研究重點項目（KJZD-K201901102）資助。

2020-08-11

2020-09-25

肖蕙蕙 女，1964年生，教授，碩士生導師，研究方向為電力電子與電力傳動、新能源發電與控制等。E-mail: xhh@cqut.edu.cn

郭 強 男，1984年生，博士，講師，研究領域為大功率變流器，新型逆變器等。E-mail: guoqiang@cqut.edu.cn（通信作者）

（編輯 陳 誠）