無(wú)線電能傳輸系統(tǒng)小信號(hào)模型降階研究

程志遠(yuǎn) 邵會(huì)文 陳 坤 眭清洋 李東東

無(wú)線電能傳輸系統(tǒng)小信號(hào)模型降階研究

程志遠(yuǎn) 邵會(huì)文 陳 坤 眭清洋 李東東

（上海電力大學(xué)電氣工程學(xué)院 上海 200090）

無(wú)線電能傳輸（WPT）系統(tǒng)具有高階、非線性及強(qiáng)耦合的特點(diǎn)。為準(zhǔn)確描述WPT系統(tǒng)動(dòng)態(tài)響應(yīng)，進(jìn)而實(shí)現(xiàn)控制系統(tǒng)的優(yōu)化設(shè)計(jì)與分析，該文以LCL-S電路拓?fù)錇檠芯繉?duì)象，利用廣義狀態(tài)空間平均建模方法得到WPT系統(tǒng)的大信號(hào)模型，在此基礎(chǔ)上建立系統(tǒng)高階小信號(hào)模型。同時(shí)，為簡(jiǎn)化系統(tǒng)控制器設(shè)計(jì)，采用拉蓋爾多項(xiàng)式展開(kāi)與平衡理論相結(jié)合的方法，對(duì)高階小信號(hào)模型進(jìn)行降階處理，即將11階系統(tǒng)降為3階。仿真與實(shí)驗(yàn)結(jié)果表明，降階系統(tǒng)與全階系統(tǒng)具有相似的動(dòng)態(tài)響應(yīng)及小擾動(dòng)穩(wěn)定性，驗(yàn)證了降階模型的有效性與準(zhǔn)確性，為WPT控制系統(tǒng)的設(shè)計(jì)奠定了模型基礎(chǔ)。

無(wú)線電能傳輸 小信號(hào)模型 平衡實(shí)現(xiàn) 模型降階

0 引言

無(wú)線電能傳輸（Wireless Power Transfer, WPT）技術(shù)通過(guò)高頻磁場(chǎng)構(gòu)建能量傳輸通道，能在非導(dǎo)電介質(zhì)之間傳輸電能，避免了機(jī)械式的連接方式，且具有耐高溫、耐腐蝕、安全可靠性高等諸多優(yōu)點(diǎn)，近年來(lái)在電動(dòng)汽車(chē)、醫(yī)療植入設(shè)備、自主式水下機(jī)器人（Autonomous Underwater Vehicle, AUV）等領(lǐng)域得到了廣泛研究[1-6]。

由于無(wú)線電能傳輸系統(tǒng)通過(guò)松耦合變壓器實(shí)現(xiàn)氣隙傳能，為最大限度地減少漏磁及滿足直流負(fù)載需求，需引入諧振與不控整流環(huán)節(jié)，使得系統(tǒng)具有高階、非線性及強(qiáng)耦合的特點(diǎn)，極大地增加了控制器的設(shè)計(jì)難度與復(fù)雜性。目前針對(duì)WPT系統(tǒng)控制器設(shè)計(jì)，主要基于建模與控制算法的研究，且為了獲取系統(tǒng)優(yōu)良的動(dòng)態(tài)性能，系統(tǒng)建模應(yīng)最大限度地接近于實(shí)際。為滿足這一需求，現(xiàn)有針對(duì)WPT系統(tǒng)的建模方法主要有狀態(tài)空間平均（State Space Average, SSA）、廣義狀態(tài)空間平均（Generalized SSA, GSSA）、頻閃映射方法[7]和拓展描述函數(shù)法。其中，廣義狀態(tài)空間平均法能夠精確地描述15階以下變換器系統(tǒng)各狀態(tài)變量的動(dòng)態(tài)響應(yīng)，文獻(xiàn)[8]基于此方法建立了雙向WPT系統(tǒng)狀態(tài)空間模型。文獻(xiàn)[9-10]使用拓展函數(shù)法，對(duì)于SS拓?fù)涞腤PT系統(tǒng)進(jìn)行建模，得到了一個(gè)9階的小信號(hào)模型。

然而系統(tǒng)階數(shù)過(guò)高會(huì)增加控制系統(tǒng)設(shè)計(jì)的難度。因此針對(duì)系統(tǒng)模型降階的研究得以重視。模型降階即在保證動(dòng)態(tài)特性及穩(wěn)定性與原系統(tǒng)相似的條件下，利用低階模型代替原高階系統(tǒng)，采用該方法可極大地簡(jiǎn)化系統(tǒng)控制器設(shè)計(jì)。文獻(xiàn)[11]采用Krylov子空間的降階方法對(duì)配電網(wǎng)絡(luò)進(jìn)行降階，但缺點(diǎn)在于算法較為復(fù)雜，且無(wú)法保證系統(tǒng)的可控與可觀性。文獻(xiàn)[12]運(yùn)用平衡理論的方法將電力系統(tǒng)模型進(jìn)行降階，得到的降階系統(tǒng)很好地保留了原系統(tǒng)的動(dòng)態(tài)過(guò)程和穩(wěn)定性。文獻(xiàn)[13]同樣采用平衡理論的方法針對(duì)模塊化多電平變換器進(jìn)行降階并設(shè)計(jì)控制器，為預(yù)估與改善系統(tǒng)的不穩(wěn)定性提供了便捷。目前，系統(tǒng)降階在無(wú)線電能傳輸領(lǐng)域中研究較少，如文獻(xiàn)[14]針對(duì)WPT系統(tǒng)進(jìn)行小信號(hào)建模，為了驗(yàn)證所設(shè)計(jì)控制器性能，僅對(duì)模型的零極點(diǎn)分布進(jìn)行了研究，但整體的控制仿真系統(tǒng)仍采用階數(shù)較高的小信號(hào)模型結(jié)構(gòu)。文獻(xiàn)[15]將WPT系統(tǒng)中LC諧振部分視作一個(gè)電感元件，采用場(chǎng)振幅與場(chǎng)相位對(duì)等效電感元件進(jìn)行描述，從而成功地將9階小信號(hào)模型降為5階系統(tǒng)，但該方法理論體系較為復(fù)雜，缺乏一定的適用性，且系統(tǒng)所降階次仍然較高。文獻(xiàn)[16]采用閉環(huán)主導(dǎo)極點(diǎn)法，將WPT系統(tǒng)由11階等效為2階系統(tǒng)，由于只考慮了主導(dǎo)極點(diǎn)，在動(dòng)態(tài)特性與穩(wěn)態(tài)誤差上無(wú)法保證與原系統(tǒng)高度匹配，同時(shí)閉環(huán)主導(dǎo)極點(diǎn)法源于經(jīng)典控制理論，故僅針對(duì)單輸入單輸出系統(tǒng)，應(yīng)用上具有一定的局限性。

本文首先基于LCL-S拓?fù)浣Y(jié)構(gòu)的WPT系統(tǒng)進(jìn)行小信號(hào)建模，采用拉蓋爾多項(xiàng)式展開(kāi)與平衡理論相結(jié)合，對(duì)全階小信號(hào)模型進(jìn)行了降階處理；然后針對(duì)降階后不同階數(shù)與全階系統(tǒng)進(jìn)行對(duì)比分析，得出有利于控制器設(shè)計(jì)的等效三階模型；最后，通過(guò)仿真與實(shí)驗(yàn)驗(yàn)證了降階后小信號(hào)模型與全階系統(tǒng)高相似度的特點(diǎn)。

1 WPT系統(tǒng)模型建立

圖1所示為L(zhǎng)CL-S拓?fù)浣Y(jié)構(gòu)的WPT系統(tǒng)的等效電路。其中，1、p和s分別是1、p和s的內(nèi)阻，f是輸出側(cè)濾波電容,H為逆變器輸出電壓，對(duì)其進(jìn)行傅里葉級(jí)數(shù)展開(kāi)，得到基波幅值B，其值為

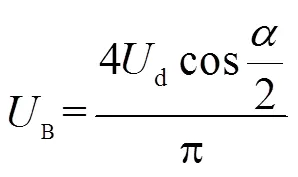
式中，為逆變器移相角；Ud為逆變器輸入側(cè)電壓。

通過(guò)LCL-S型拓?fù)浣Y(jié)構(gòu)的濾波后，逆變器輸出電壓的基波分量B提供了主要功率輸出的功能，所以采用B代替逆變器輸出電壓。此外，用方波電壓源rec與電流源rec來(lái)等效表示整流電路部分[17]。

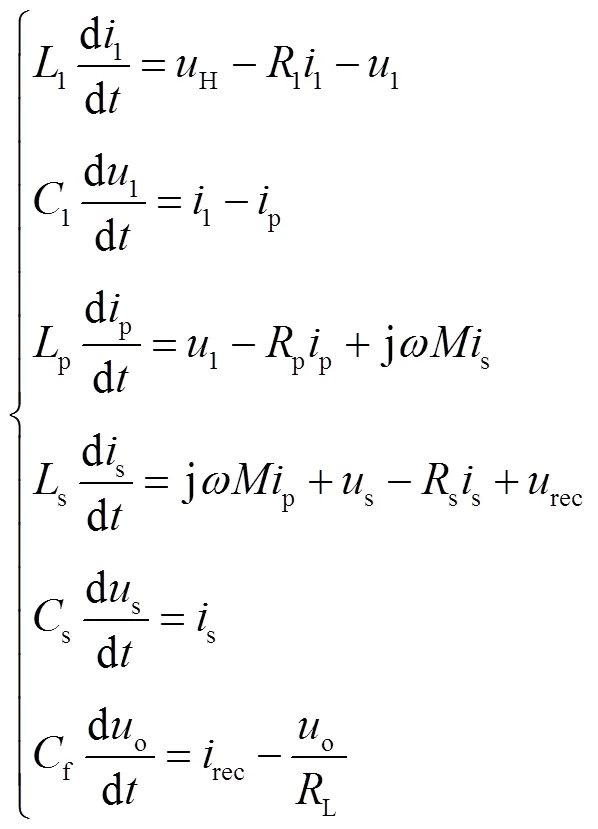
以逆變器輸出電壓為零相位參考，逆變器輸出電壓和其他狀態(tài)變量[18]可表示為

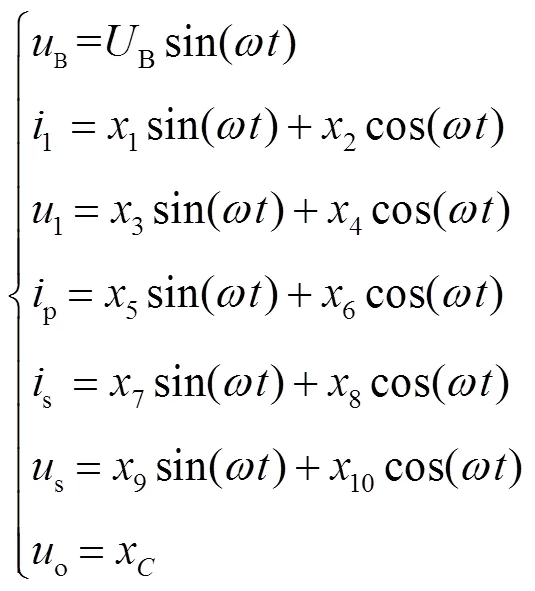
式中，奇數(shù)項(xiàng)為正弦分量幅值；偶數(shù)項(xiàng)為余弦分量幅值；為濾波電容的電壓有效值。

由于WPT系統(tǒng)副邊諧振網(wǎng)絡(luò)工作在額定頻率附近，且rec為方波信號(hào)，通過(guò)傅里葉展開(kāi)可得無(wú)數(shù)的奇次諧波，因此可將3次及以上諧波濾除[19]，其基波分量為

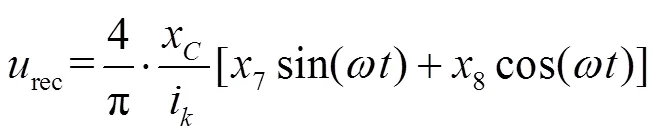
由于整流橋的輸入輸出功率守恒，可得整流部分輸出電流rec為

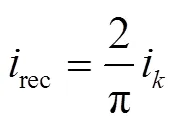
其中，的表達(dá)式為

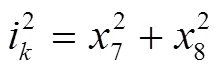
選取狀態(tài)變量

將式（3）～式（6）代入式（2）可建立系統(tǒng)的廣義狀態(tài)空間平均模型為

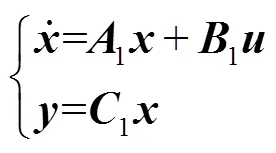
式中，1∈R11×11，1∈R11×1，1∈R1×11，其值分別為附錄中式（A1）、式（A2）與式（A3）。式（7）即為諧振電路大信號(hào)模型，令微分項(xiàng)為零可得到系統(tǒng)在穩(wěn)態(tài)點(diǎn)時(shí)各個(gè)狀態(tài)變量的幅值大小。

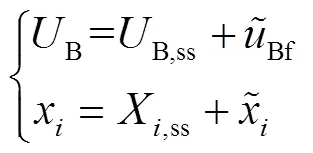
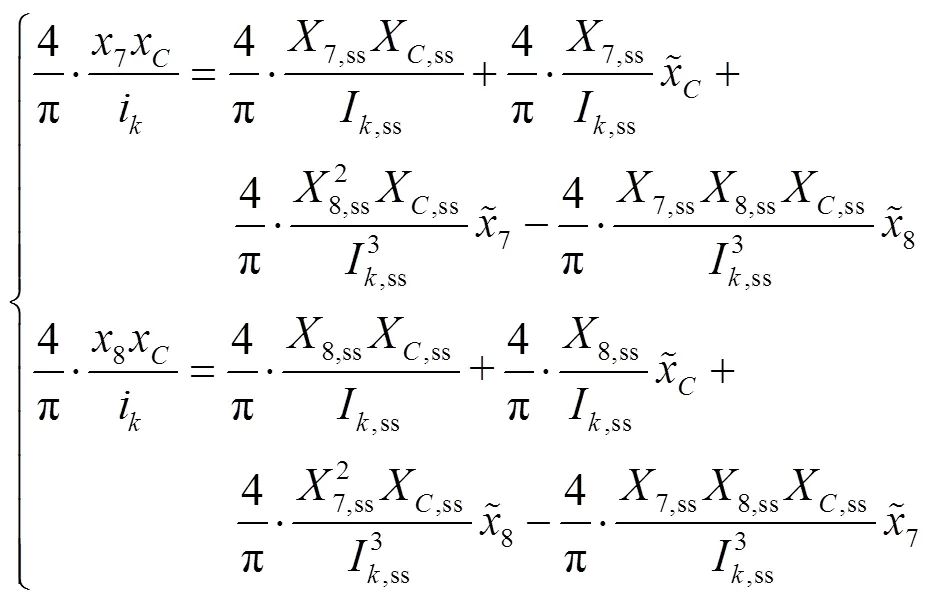
其中

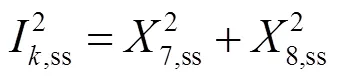
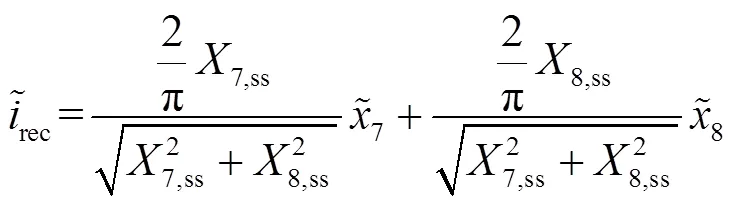
將式（8）～式（11）與式（7）結(jié)合，現(xiàn)以=[12345678910x]為狀態(tài)變量建立小信號(hào)模型，即

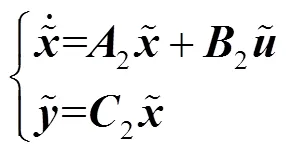
式中，2∈R11×11，2∈R11×1，2∈R1×11，2、2、2值分別為附錄中式（A4）、式（A2）和式（A3）；參數(shù)k（=1,…,5）見(jiàn)附錄式（A5）。

2 模型降階及其實(shí)現(xiàn)

本文基于平衡理論和Hankel奇異值降階思想對(duì)系統(tǒng)模型進(jìn)行降階，在保證系統(tǒng)動(dòng)態(tài)特性基本不變的條件下，利用低階系統(tǒng)代替原高階系統(tǒng)。

2.1 平衡實(shí)現(xiàn)及平衡截?cái)喾?/h3>

平衡實(shí)現(xiàn)是將原高階系統(tǒng)模型轉(zhuǎn)換為平衡系統(tǒng)后，通過(guò)奇異值分解得到降階模型，即通過(guò)選取適當(dāng)映射子空間得到高性能降階模型的降階方法[20]。

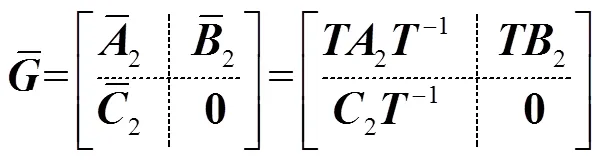
若系統(tǒng)同時(shí)滿足式（15），則可認(rèn)為式（14）是WPT系統(tǒng)小信號(hào)模型的平衡系統(tǒng)。

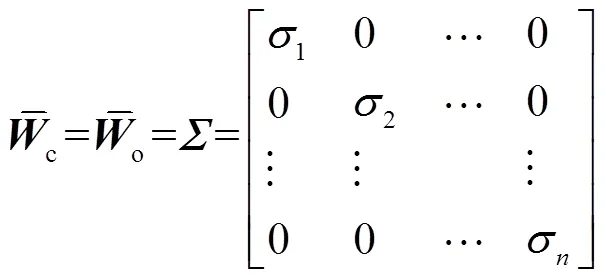
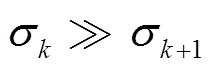
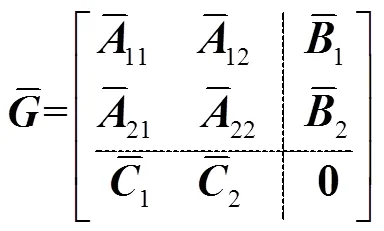
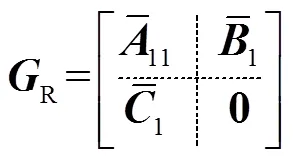
上述平衡截?cái)喾ㄊ峭ㄟ^(guò)求解Lyapunov方程來(lái)得到系統(tǒng)的可控格蘭姆矩陣c和可觀格蘭姆矩陣o，存在計(jì)算復(fù)雜度高，求解過(guò)程時(shí)間長(zhǎng)的缺點(diǎn)。鑒于拉蓋爾多項(xiàng)式展開(kāi)法在滿足一定精度的條件下可將矩陣指數(shù)進(jìn)行近似求解，具有求解過(guò)程高效的優(yōu)點(diǎn)，故本文采用該方法解決問(wèn)題。

2.2 拉蓋爾展開(kāi)

系統(tǒng)的狀態(tài)轉(zhuǎn)移矩陣又稱(chēng)作矩陣指數(shù)，即e。本文采用的方法是基于拉蓋爾多項(xiàng)式將e進(jìn)行展開(kāi)，從而簡(jiǎn)化平衡截?cái)喾椒ㄖ锌煽馗裉m姆矩陣c與可觀格蘭姆矩陣o的求解。

拉蓋爾多項(xiàng)式可表示為

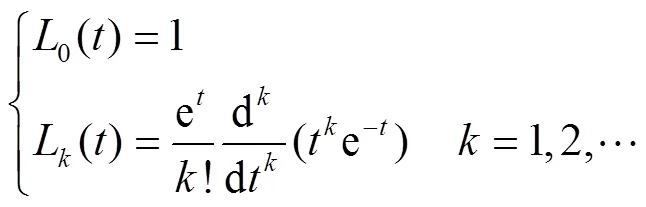
對(duì)指數(shù)函數(shù)e進(jìn)行拉蓋爾多項(xiàng)式級(jí)數(shù)展開(kāi)可得

其中，a滿足

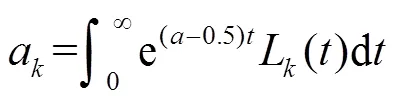
將拉蓋爾多項(xiàng)式進(jìn)行拉普拉斯變換可得[22]

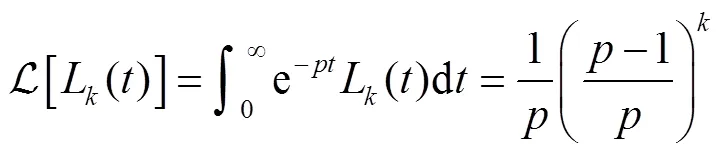
令=-(0.5)，代入式（21）能夠得到遞歸形式為

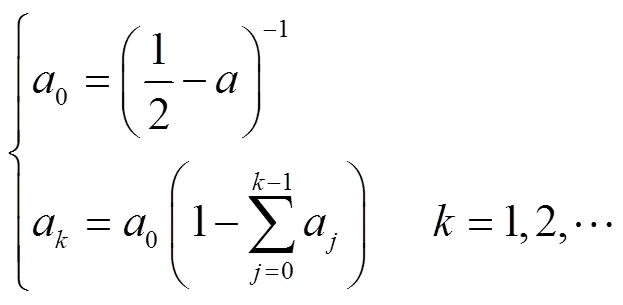
進(jìn)行上述推導(dǎo)后，所得遞歸形式可類(lèi)似地應(yīng)用于全階小信號(hào)系統(tǒng)的狀態(tài)轉(zhuǎn)移矩陣。

2.3 高階小信號(hào)系統(tǒng)降階求解

基于拉蓋爾多項(xiàng)式展開(kāi)的求解方法，首先對(duì)式（13）中的矩陣e2進(jìn)行近似展開(kāi)為

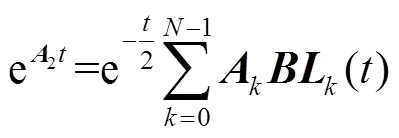
由2.2節(jié)可知，其中

將式（23）與式（24）代入到式（13）中可得

由拉蓋爾多項(xiàng)式的正交性，可以得到系統(tǒng)可控格蘭姆矩陣的低秩分解為

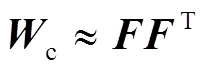
同理，可觀格蘭姆矩陣能夠得到低秩分解為

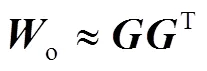
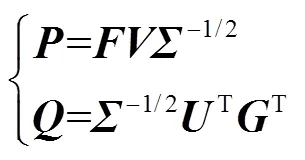
通過(guò)投影變換得到平衡系統(tǒng)

用平衡截?cái)喾▽?duì)平衡系統(tǒng)進(jìn)行截?cái)嗵幚恚Ａ魧?duì)系統(tǒng)輸入輸出影響較大的狀態(tài)變量，舍去冗余部分，即可得到基于拉蓋爾多項(xiàng)式展開(kāi)方法的小信號(hào)模型降階系統(tǒng)。

3 仿真分析

本文以LCL-S拓?fù)涞腤PT系統(tǒng)為研究對(duì)象，其仿真模型參數(shù)見(jiàn)表1。

表1 WPT系統(tǒng)仿真參數(shù)

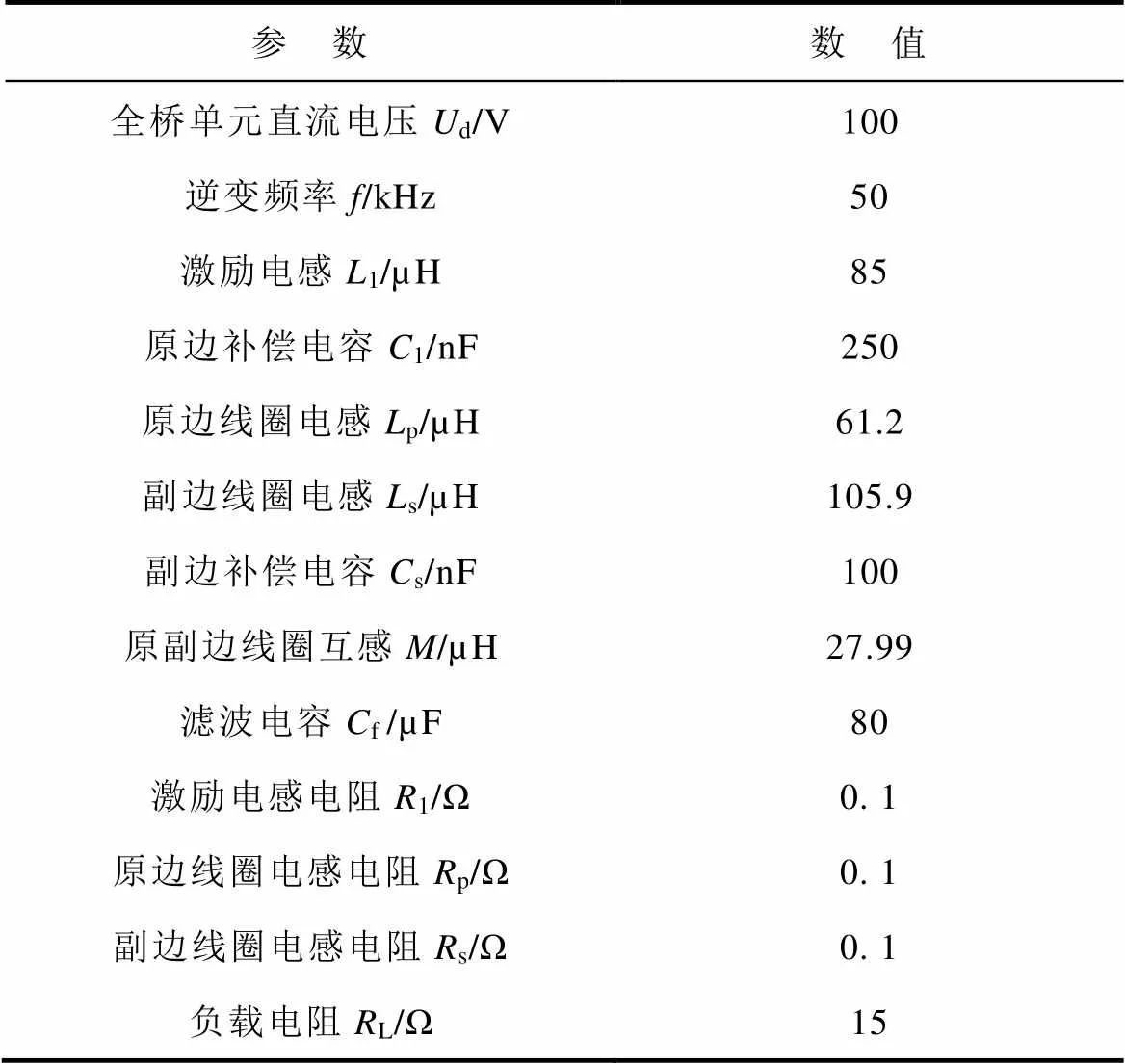
Tab.1 Simulation parameters of the WPT system

根據(jù)所給參數(shù)，采用上述理論分析對(duì)系統(tǒng)進(jìn)行降階，全階小信號(hào)模型的階數(shù)為11階，降階處理后得到系統(tǒng)階數(shù)與Hankel奇異值對(duì)應(yīng)關(guān)系如圖2所示。顯然，前5個(gè)狀態(tài)占了系統(tǒng)總信息99%以上，后6個(gè)狀態(tài)的Hankel奇異值遠(yuǎn)遠(yuǎn)小于前5個(gè)狀態(tài)的奇異值。因此，以下仿真中將分別針對(duì)1～5階系統(tǒng)，從時(shí)域與頻域等方面進(jìn)行分析，比較各階數(shù)系統(tǒng)與全階系統(tǒng)的匹配程度。

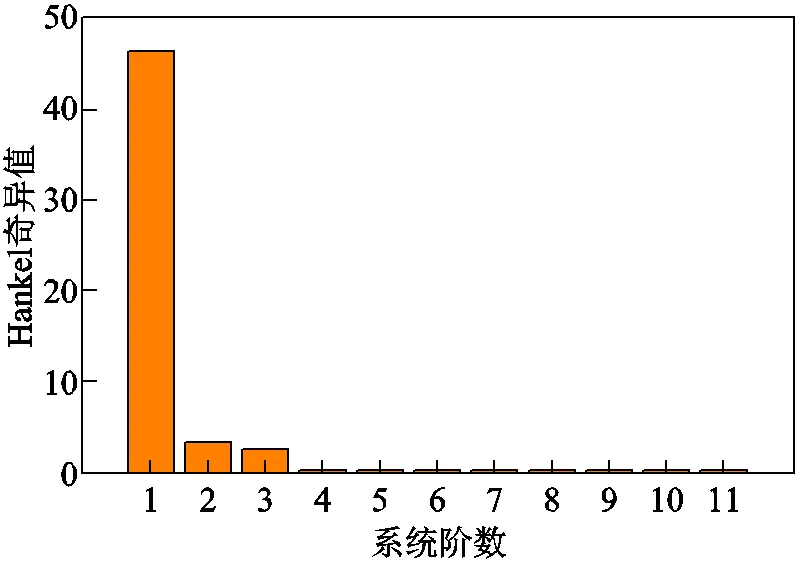
圖2 Hankel奇異值

采用表1所示參數(shù)，移相角從180°階躍至 0°的條件下，從時(shí)域角度對(duì)原系統(tǒng)與降階系統(tǒng)的輸出動(dòng)態(tài)行為與穩(wěn)態(tài)值進(jìn)行分析，響應(yīng)如圖3所示。

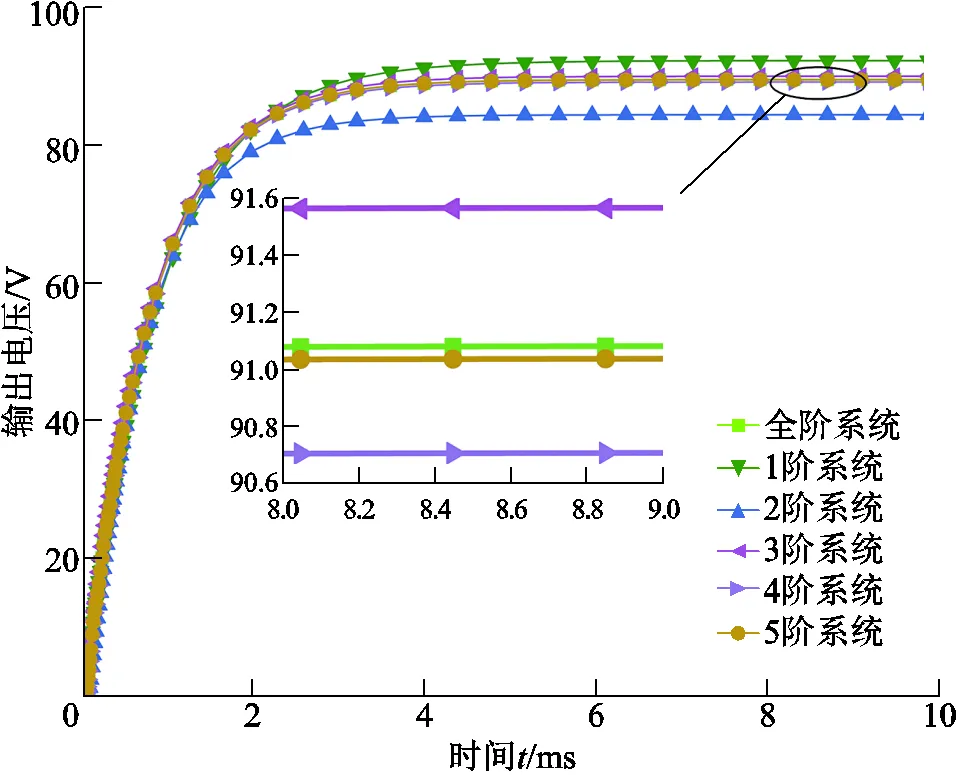
圖3 全階與各降階系統(tǒng)的階躍響應(yīng)曲線

由圖3可以看出，5階系統(tǒng)與全階系統(tǒng)的系統(tǒng)響應(yīng)曲線基本一致，3、4階系統(tǒng)的輸出響應(yīng)較原系統(tǒng)曲線誤差也較小，偏差在0.6V以下。而1、2階系統(tǒng)的穩(wěn)態(tài)時(shí)誤差相對(duì)較大。

為了定量地分析各降階系統(tǒng)與原系統(tǒng)的匹配程度，本文采用皮爾遜相關(guān)系數(shù)來(lái)進(jìn)行計(jì)算與分析，其取值在-1～1之間，絕對(duì)值越大，說(shuō)明二者相關(guān)性越強(qiáng)，其公式為

式中，為數(shù)據(jù)點(diǎn)個(gè)數(shù)；x、y分別為第個(gè)節(jié)點(diǎn)數(shù)據(jù)；為皮爾遜相關(guān)系數(shù)。

各降階系統(tǒng)與全階小信號(hào)系統(tǒng)動(dòng)態(tài)響應(yīng)波形的皮爾遜相關(guān)系數(shù)見(jiàn)表2，由數(shù)據(jù)可以看出3～5階系統(tǒng)的響應(yīng)曲線與全階系統(tǒng)的匹配程度較高。

表2 降階系統(tǒng)動(dòng)態(tài)響應(yīng)皮爾遜相關(guān)系數(shù)

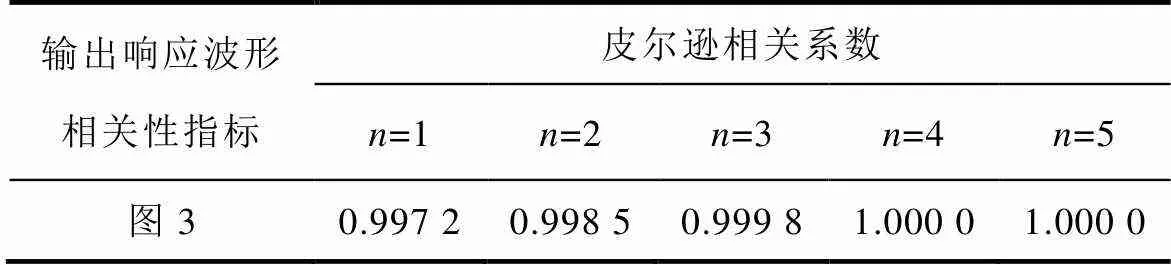
Tab.2 Pearson correlation coefficient of dynamic response of reduced-order system

為了進(jìn)一步分析3～5階系統(tǒng)與全階系統(tǒng)的匹配程度，圖4與圖5分別給出降階前后模型的極點(diǎn)分布與伯德圖。

圖4 全階與3～5階系統(tǒng)極點(diǎn)分布

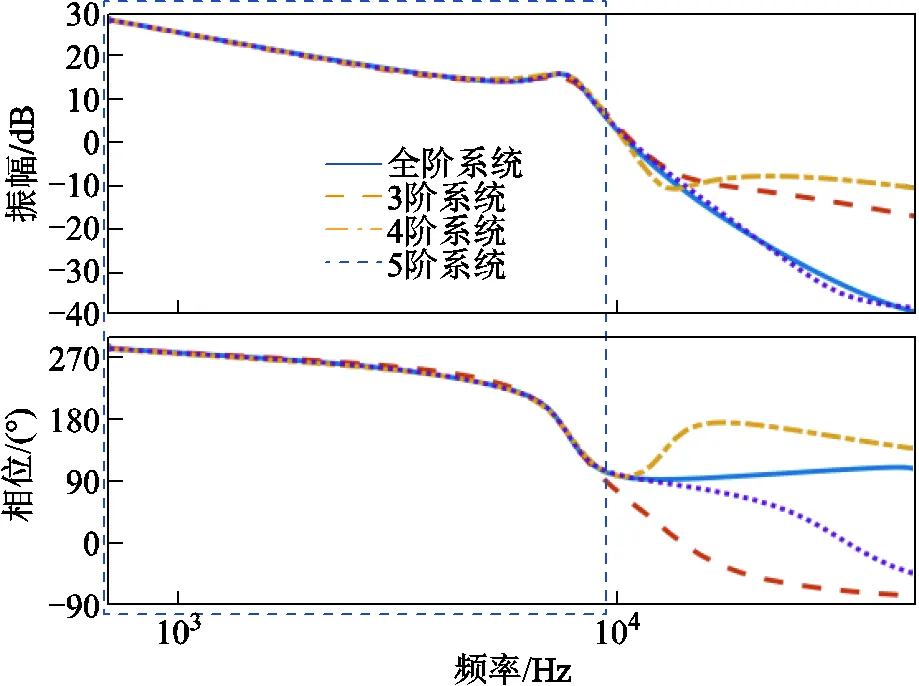
圖5 全階與3～5階系統(tǒng)的伯德圖

由圖4可知，3階降階系統(tǒng)與全階系統(tǒng)主導(dǎo)極點(diǎn)具有較高的相似性，即瞬態(tài)響應(yīng)趨于一致，且從伯德圖中可以看出，降階系統(tǒng)與全階系統(tǒng)重疊的部分接近10kHz。因此，為了大大簡(jiǎn)化一定頻率范圍內(nèi)控制器的分析和設(shè)計(jì)，可將全階系統(tǒng)用3階降階系統(tǒng)來(lái)表征與模擬。

3 實(shí)驗(yàn)驗(yàn)證

為驗(yàn)證所得模型的可靠性，現(xiàn)搭建如圖6所示基于LCL-S拓?fù)浣Y(jié)構(gòu)的無(wú)線電能傳輸實(shí)驗(yàn)平臺(tái)。

圖6 無(wú)線充電裝置實(shí)驗(yàn)平臺(tái)

圖7是輸入直流電壓100V，負(fù)載為15Ω，移相角為0°時(shí)原邊逆變與副邊整流輸出電壓與電流波形，可以看出系統(tǒng)逆變側(cè)輸出電流滯后于移相電壓，處于弱感性狀態(tài)，這為系統(tǒng)能夠工作在軟開(kāi)關(guān)狀態(tài)下提供了條件。

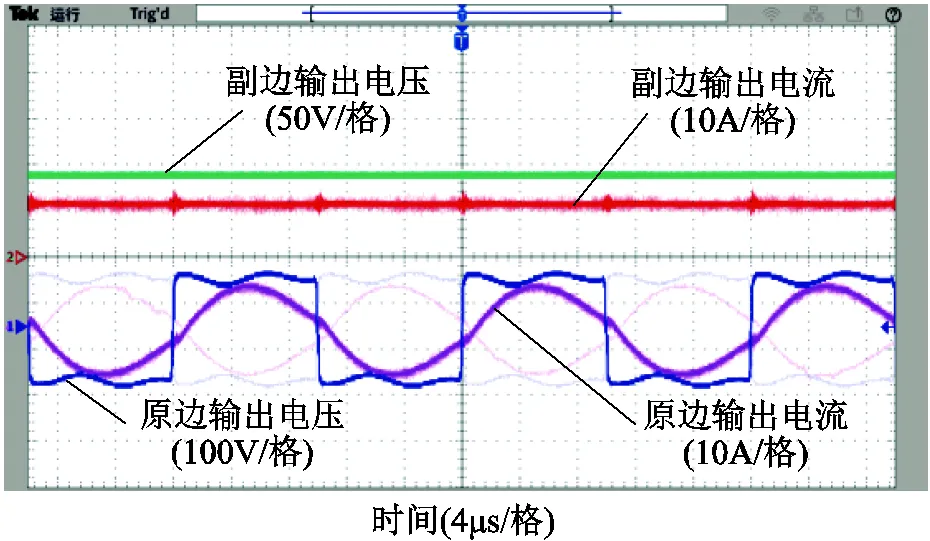
圖7 原邊逆變與副邊整流輸出電壓與電流波形

圖8是移相角從180°階躍至0°時(shí)實(shí)驗(yàn)平臺(tái)的負(fù)載電壓與三階系統(tǒng)仿真波形的對(duì)比，其穩(wěn)態(tài)誤差僅為1.71V，可滿足基本精度需求。二者的皮爾遜相關(guān)系數(shù)為0.792 2（系數(shù)在±(0.5～1)以內(nèi)即為強(qiáng)相關(guān)）。因此認(rèn)為降階模型能夠有效地模擬全階系統(tǒng)。

圖8 降階模型仿真與實(shí)驗(yàn)波形

為驗(yàn)證降階系統(tǒng)在頻域上的匹配程度，采用數(shù)字控制方法，通過(guò)控制器產(chǎn)生穩(wěn)態(tài)移相角的同時(shí)疊加幅值一定但頻率不同的小信號(hào)移相角，而后通過(guò)示波器的FFT分析采集統(tǒng)一頻率下的輸出響應(yīng)與小信號(hào)移相角的信號(hào)增益大小，從而繪制出仿真全階、3階系統(tǒng)和實(shí)驗(yàn)平臺(tái)的開(kāi)環(huán)伯德圖如圖9所示。由圖9可以看出，實(shí)際與仿真系統(tǒng)的幅頻響應(yīng)吻合較好，但存在一定的偏差。降階模型與實(shí)驗(yàn)平臺(tái)在時(shí)域和頻域均存在一定誤差，造成這種偏差的原因?yàn)椋簩?shí)驗(yàn)平臺(tái)中的器件可能存在雜散參數(shù)，在運(yùn)行過(guò)程中影響系統(tǒng)的動(dòng)態(tài)特性；在小信號(hào)模型分析建模時(shí)所采用的線性化方法使得系統(tǒng)存在一部分的失真。

圖9 仿真與實(shí)驗(yàn)系統(tǒng)伯德圖

4 結(jié)論

1）本文建立了基于LCL-S電路拓?fù)涞臒o(wú)線電能傳輸系統(tǒng)小信號(hào)模型，采用拉蓋爾多項(xiàng)式展開(kāi)與平衡截?cái)嘞嘟Y(jié)合的方法，使原11階系統(tǒng)降至3階系統(tǒng)，通過(guò)仿真對(duì)比了全階系統(tǒng)、1～5階系統(tǒng)在穩(wěn)態(tài)工作點(diǎn)處的動(dòng)態(tài)階躍響應(yīng)。結(jié)果表明，5階與全階系統(tǒng)響應(yīng)曲線基本一致，3、4階系統(tǒng)的輸出響應(yīng)較原系統(tǒng)偏差也僅在0.6V以下。驗(yàn)證了降階模型的有效性和準(zhǔn)確性。

2）針對(duì)本文所設(shè)計(jì)的無(wú)線電能傳輸系統(tǒng)，3階降階系統(tǒng)與全階系統(tǒng)主導(dǎo)極點(diǎn)具有較高的相似性，使得3階模型基本保留原模型的動(dòng)態(tài)特性，并且最終都趨于平穩(wěn)，達(dá)到降階且保持原系統(tǒng)性能近似不變的目的。因此，可將全階系統(tǒng)用3階降階系統(tǒng)來(lái)表征與模擬全階系統(tǒng)，進(jìn)而極大地簡(jiǎn)化一定頻率范圍內(nèi)控制系統(tǒng)的分析和設(shè)計(jì)。

3）本文所采用的小信號(hào)建模及與之相對(duì)應(yīng)的降階方法，可應(yīng)用于不同電路拓?fù)涞臒o(wú)線電能傳輸控制系統(tǒng)的設(shè)計(jì)，具有一定的普適性。

附 錄

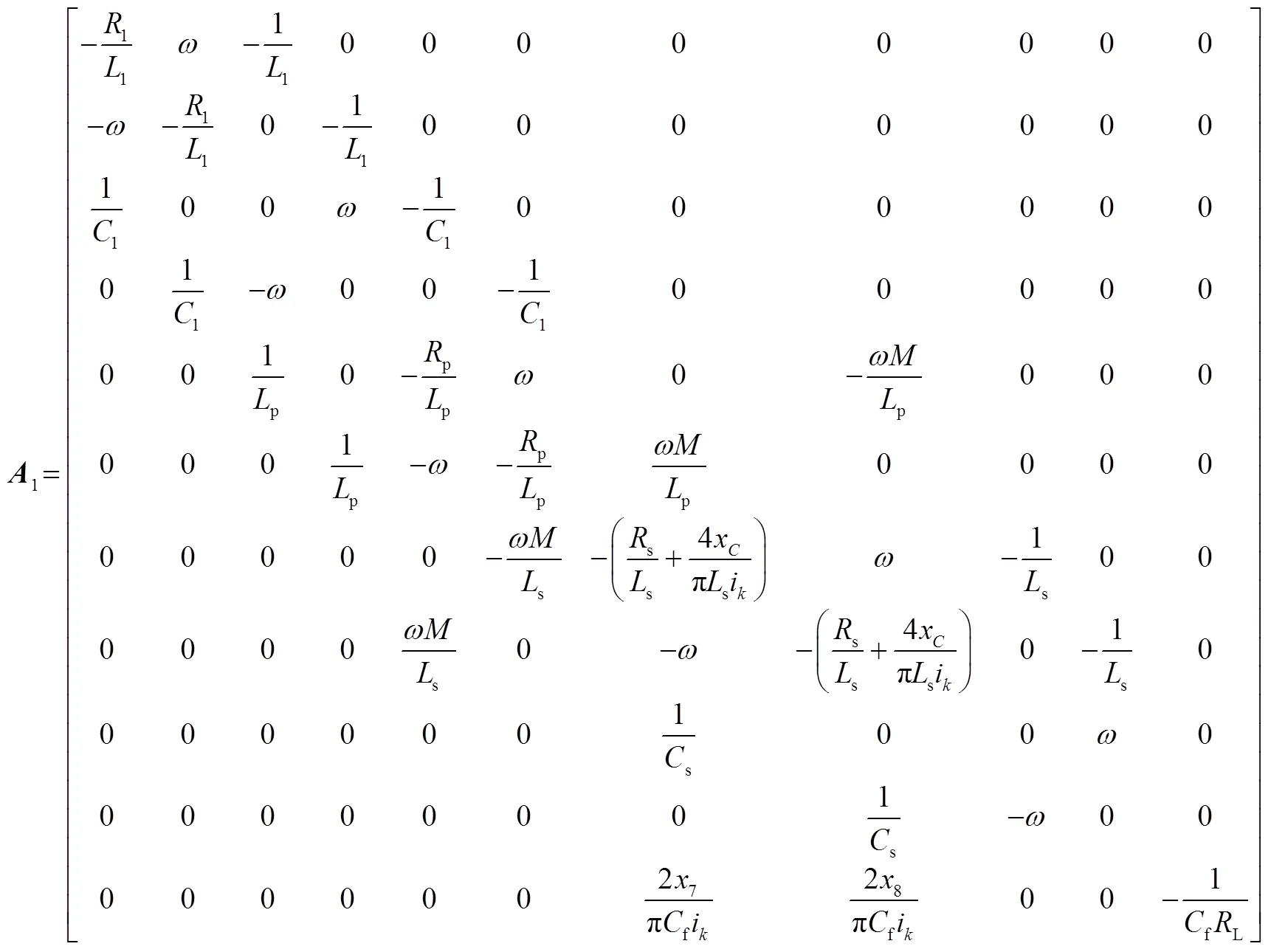
1、2表達(dá)式為

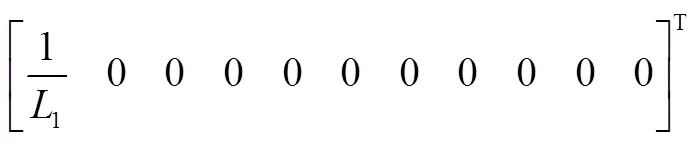
1、2表達(dá)式為

[1] 薛明, 楊慶新, 章鵬程, 等. 無(wú)線電能傳輸技術(shù)應(yīng)用研究現(xiàn)狀與關(guān)鍵問(wèn)題[J]. 電工技術(shù)學(xué)報(bào), 2021, 36(8): 1547-1568.

Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.

[2] 范興明, 高琳琳, 莫小勇, 等. 無(wú)線電能傳輸技術(shù)的研究現(xiàn)狀與應(yīng)用綜述(英文)[J]. 電工技術(shù)學(xué)報(bào), 2019, 34(7): 1353-1380.

Fan Xingming, Gao Linlin, Mo Xiaoyong, et al. Overview of research status and application of wireless power transmission technology[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(7): 1353-1380.

[3] 張獻(xiàn), 任年振, 楊慶新, 等. 電動(dòng)汽車(chē)無(wú)線充電自整定控制[J]. 電工技術(shù)學(xué)報(bào), 2020, 35(23): 4825- 4834.

Zhang Xian, Ren Nianzhen, Yang Qingxin, et al. Research on self-tuning control strategy of wireless charging for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4825- 4834.

[4] Zhen Z, Pang H, Georgiadis A, et al. Wireless power transfer—an overview[J]. IEEE Transactions on Industrial Electronics, 2018, 66(2): 1044-1058.

[5] 蔡春偉, 武帥, 張言語(yǔ), 等. 基于弧形線圈結(jié)構(gòu)的無(wú)線充電系統(tǒng)能量傳輸與控制[J]. 電工技術(shù)學(xué)報(bào), 2020, 35(14): 2959-2968.

Cai Chunwei, Wu Shuai, Zhang Yanyu, et al. Power transfer and control of wireless charging system based on an arc coil structure[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2959- 2968.

[6] 卿曉東, 蘇玉剛. 電場(chǎng)耦合無(wú)線電能傳輸技術(shù)綜述[J]. 電工技術(shù)學(xué)報(bào), 2021, 36(17): 3649-3663.

Qing Xiaodong, Su Yugang. An overview of electric- filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.

[7] 代云中, 何凱瑞, 杜程茂, 等. LC濾波H6結(jié)構(gòu)逆變器離散模型簡(jiǎn)化與動(dòng)力學(xué)行為[J]. 高電壓技術(shù), 2017, 43(10): 3313-3321.

Dai Yunzhong, He Kairui, Du Chengmao, et al. Discrete model simplification and dynamic behavior of LC-filter-based inverter with H6 type[J]. High Voltage Engineering, 2017, 43(10): 3313-3321.

[8] Hu A P. Modeling a contactless power supply using GSSA method[C]//Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australlia, 2009: 10-13.

[9] Zahid Z U, Dalala Z M, Cong Z. Modeling and control of series–series compensated inductive power transfer system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 111-123.

[10] Huang Zhicong, Wong Siu-Chung, Tse C K. Control design for optimizing efficiency in inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2017, 33(5): 4523-4534.

[11] 李鵬, 于浩, 王成山, 等. 基于Krylov子空間的大規(guī)模配電網(wǎng)絡(luò)模型整體化簡(jiǎn)方法[J]. 電網(wǎng)技術(shù), 2013, 37(8): 2343-2348.

Li Peng, Yu Hao, Wang Chengshan, et al. Model order reduction of large scale distribution grid based on Krylov subspace method[J]. Power System Tech- nology, 2013, 37(8): 2343-2348.

[12] 張喆, 趙洪山, 李志為, 等. 平衡格萊姆方法在電力系統(tǒng)線性模型降階中的應(yīng)用[J]. 電工技術(shù)學(xué)報(bào), 2013, 28(6): 201-207.

Zhang Zhe, Zhao Hongshan, Li Zhiwei, et al. Power system linear model reduction based on the balanced gramian method[J]. Transactions of China Electrote- chnical Society, 2013, 28(6): 201-207.

[13] 李正, 郝全睿, 尹曉東, 等. 模塊化多電平換流器的降階小信號(hào)模型研究[J]. 中國(guó)電機(jī)工程學(xué)報(bào), 2018, 38(12): 3638-3650.

Li Zheng, Hao Quanrui, Yin Xiaodong, et al. Research on reduced-order small-signal model of modular multilevel converter[J]. Proceedings of the CSEE, 2018, 38(12): 3638-3650.

[14] Aditya K, Williamson S S. Simplified mathematical modelling of phase-shift controlled series-series compensated inductive power transfer system[C]// 2016 IEEE 25th International Symposium on Indu- strial Electronics (ISIE), Santa Clara, CA, USA, 2016: 8-10.

[15] Li Hongchang, Wang Kangping, Huang Lang, et al. Dynamic modeling based on coupled modes for wireless power transfer systems[J]. IEEE Transa- ctions on Power Electronics, 2015, 30(11): 6245- 6253.

[16] Feng H, Lukic S M. Reduced-order modeling and design of single stage LCL compensated IPT system for low voltage vehicle charging applications[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 3728-3739.

[17] Zahid Z U, Dalala Z M, Cong Z, et al. Modeling and control of series–series compensated inductive power transfer system[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics, 2015, 3(1): 111-123.

[18] Sanders S R, Noworolski J M. Generalized averaging method for power conversion circuits[J]. IEEE Transactions on Power Electronics, 1991, 6(2): 251-259.

[19] Borage M, Tiwari S, Kotaiah S. Analysis and design of an LCL-T resonant converter as a constant-current power supply[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1547-1554.

[20] Moore B. Principal component analysis in linear systems: controllability, observability, and model reduction[J]. IEEE Transactions on Automatic Control, 1981, 26(1): 17-32.

[21] Chang W, Smith R C. Model reduction based on modal Hankel singular values[J]. International Society for Optics and Photonics, 2004, 5383: 433-444.

[22] Moore G. Orthogonal polynomial expansions for the matrix exponential[J]. Linear Algebra and Its Appli- cations, 2011, 435(3): 537-559.

Research on Order Reduction of Small Signal Model of Wireless Power Transmission System

Cheng Zhiyuan Shao Huiwen Chen Kun Sui Qingyang Li Dongdong

（College of Electrical Engineering Shanghai University of Electric Power Shanghai 200090 China）

The wireless power transmission system has the characteristics of high level, nonlinearity, and strong coupling. To describe the dynamic response of the WPT system accurately to realize the optimal design and analysis of the control system, the report takes the LCL-S circuit topology as a research subject. Firstly, the large-signal model of the WPT system is obtained by the generalized state-space average modelling method. On the basis to establish a high-level small-signal model of the system. Also, Laguerre's expansion and balancing realization were used to reduce the level of the high-level small-signal model to obtain the low-order model and to simplify the design of the system controller. So, the third level was reduced by the eleventh level system. Simulation and experimental results show that the level-reduced system and full-level system have a similar dynamic response and small disturbance stability, which verifies the effectiveness and accuracy of the level-reduced model. And it builds a model foundation for the design of the WPT control system.

Wireless power transfer, small-signal model, balanced realization, model reduction

10.19595/j.cnki.1000-6753.tces.211079

TM712

國(guó)家自然科學(xué)基金資助項(xiàng)目（5187070548）。

2021-07-15

2021-09-09

程志遠(yuǎn) 男，1977年生，博士，高級(jí)工程師，研究方向?yàn)闊o(wú)線電能傳輸、高壓電纜無(wú)線取電。E-mail：chengzhiyuan@126.com

李東東 男，1976年生，博士，教授，研究方向?yàn)轱L(fēng)力發(fā)電與電力系統(tǒng)穩(wěn)定控制、智能用電等。E-mail：powerldd@163.com（通信作者）

（編輯 郭麗軍）