錨固隧道圍巖長期穩定性分析

孫睿澤

(中鐵十九局集團第三工程有限公司，遼寧 沈陽 110136)

0 引言

隨著國家經濟建設的蓬勃發展，交通基礎設施建設大規模展開。隧道作為公路、鐵路中的重要組成部分，其圍巖的長期穩定至關重要[1]。錨固是控制圍巖穩定的常用技術，在長期荷載作用下，錨固圍巖會產生變形或垮塌[2-3]。因此，有必要對錨固巖石的長期力學特性進行研究。

近年來，我國學者對錨固巖石的研究取得了較為豐碩的成果。宋勇軍等[4]通過單軸壓縮蠕變試驗研究了錨桿錨固巖石的長時力學特性，分析了錨固前后瞬時應變與蠕應變之間的差異。趙同彬等[5]對含雙節理裂隙的巖石進行了加錨后的單軸壓縮試驗，并基于聲發射技術對試樣的破壞過程進行了分析。車納等[6]基于顆粒離散元方法對錨桿錨固巖石拉拔段的破壞機理進行了研究，分析了錨固段長度、圍壓等因素對破壞模式的影響。劉泉生等[7]對白砂巖、大理巖進行了加錨后的剪切試驗，分析了錨固前后試樣的力學特性與破壞形式。張福明等[8]通過拉拔試驗對拉力型錨桿錨固段長度進行了試驗研究。滕俊洋等[9]通過單軸壓縮試驗對含層理加錨巖石進行了研究，分析了無錨、端錨和全長錨固3種試樣的力學特性。

綜上分析可知，已有研究成果對錨固巖石的蠕變力學特性進行了較為詳細的研究。文章在已有研究的基礎上，結合遼寧某在建隧道的工程實際，對該隧道砂巖進行了錨桿錨固前后的單軸蠕變試驗，分析了錨固前后試驗的蠕變力學特性的差異，為工程實際提供可靠的技術支持。

1 試驗介紹

1.1 試樣材料及參數選擇

將取自遼寧某在建隧道圍巖(砂巖)按國際巖石力學學會的標準進行加工，試樣尺寸為Ф50 mm × 100 mm(直徑 × 高)的標準圓柱體。試驗前先從外觀上剔除具有明顯缺陷和節理、層理的巖樣，然后通過聲波測速技術剔除縱波差異較大的巖樣。經過上述篩選后，試驗用巖樣的離散性大大降低，有效避免了因試驗材料帶來的誤差。

在錨固巖石單軸壓縮蠕變試驗中，為了較為真實地反映地下工程錨桿支護的實際情況，合理選擇錨桿及膠結材料至關重要。根據相似理論，本文試驗用錨桿的力學性能應與實際工程中的錨桿力學性能保持一致。經過反復的鋼材力學性能試驗，最終選取45號型鋼加工成的鋼絲作為錨桿，膠結材料選取環氧樹脂。在隧道等深部地下工程中，錨桿的支護參數一般為：孔徑32 mm，桿徑20 mm，間排距為800 mm × 800 mm。根據本文試件尺寸及工程實際參數，以8∶1作為幾何相似比，最終得到錨固巖石試件的幾何參數，見表1。受試驗試件高度限制，同時考慮錨桿均勻分布，取試樣三等分點沿水平方向布設兩根錨桿。

表1 錨固巖石幾何參數

1.2 錨固試件制備過程

錨固砂巖試件具體制作過程如下：

(1)首先采用游標卡尺找到錨桿準確位置，然后采用臺式鉆機對試件進行鉆孔，孔徑為4 mm；

(2)將制備好的錨桿穿過試件鉆孔，并對其進行有效張拉，考慮到錨桿的屈服強度，本文設置錨桿張拉力大小為1.7 kN；

(3)在張拉狀態下用注射器將環氧樹脂注入鉆孔內，注滿后用保鮮膜進行封堵，靜止48 h后切斷鋼絲，并將端部進行磨平處理。制備好的錨固試件見圖1。

圖1 錨固砂巖試件

1.3 試驗設備及方法

本文錨固前后砂巖單軸蠕變試驗均在中國科學院武漢巖土力學研究所研制的全自動巖石類材料三軸試驗系統上完成，試驗在恒溫恒濕條件下進行，溫度控制在(26±0.5) ℃。單軸蠕變試驗方法采用單試件逐級增量加載法，試驗前需對錨固砂巖試樣進行單軸加載試驗，得到單軸抗壓強度為75.41 MPa，以此來確定蠕變分級加載應力水平。首先對試樣施加軸向荷載至指定應力水平，待變形趨于穩定后施加下一級應力水平，以此類推，直至施加至最后一級應力水平，試樣破壞，導出數據，分析試驗結果。

2 試驗結果分析

本文錨固前后砂巖試樣共經歷了7級應力水平，歷時86 h。圖2為砂巖錨固前后軸向、徑向分級加載蠕變曲線。從圖中可以看出，砂巖錨固前后均具有顯著的蠕變特性，且錨固砂巖的蠕變變形情況得到了有效改善。同一荷載水平下，軸向、徑向錨固試樣的變形量均小于錨固前試樣的變形量，且錨固對于徑向變形的敏感性大于軸向變形，說明錨固對試樣的徑向變形起到了明顯的約束作用。

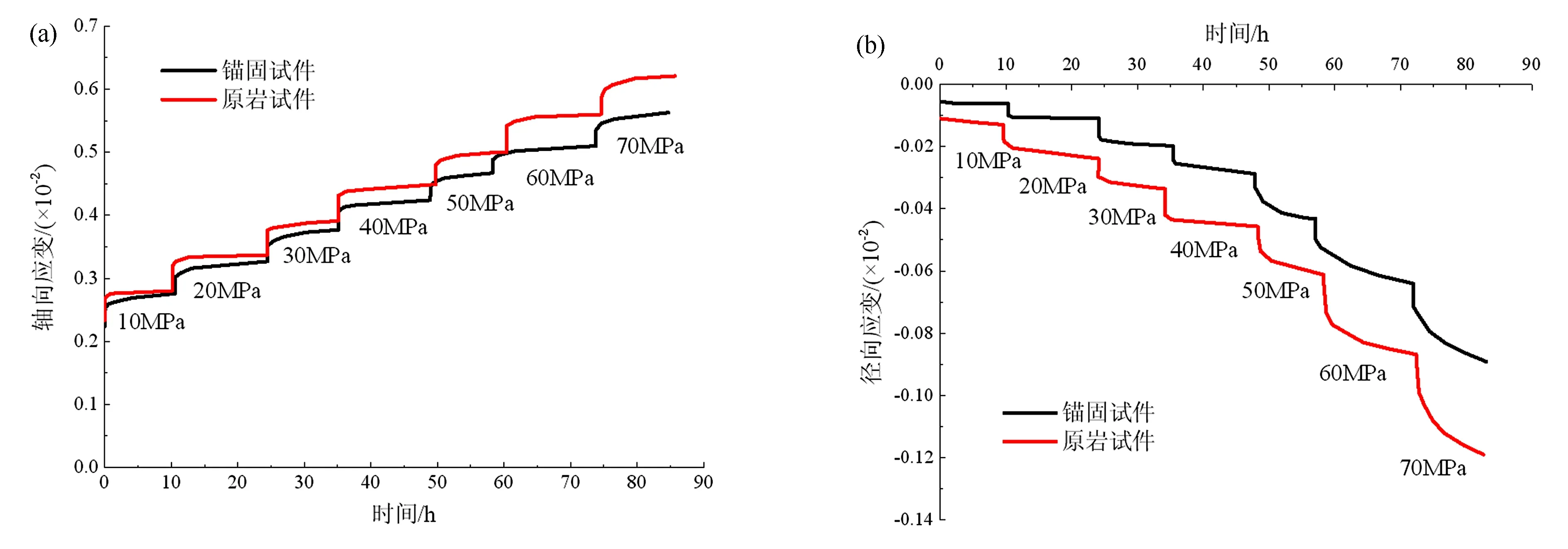
圖2 錨固前后砂巖分級加載蠕變曲線

根據蠕變試驗結果，提取不同應力水平下錨固前后砂巖的軸向、徑向瞬時應變與蠕應變，繪制錨固前后砂巖軸向瞬時應變、蠕應變隨應力水平的分布曲線，如圖3所示。從圖中可以看出，錨固前后砂巖的軸向瞬時應變均隨應力水平呈先減小后增大的變化趨勢，而蠕應變則呈逐漸遞增變化趨勢。不同應力水平下，錨固后砂巖的瞬時應變和蠕應變均小于錨固前。

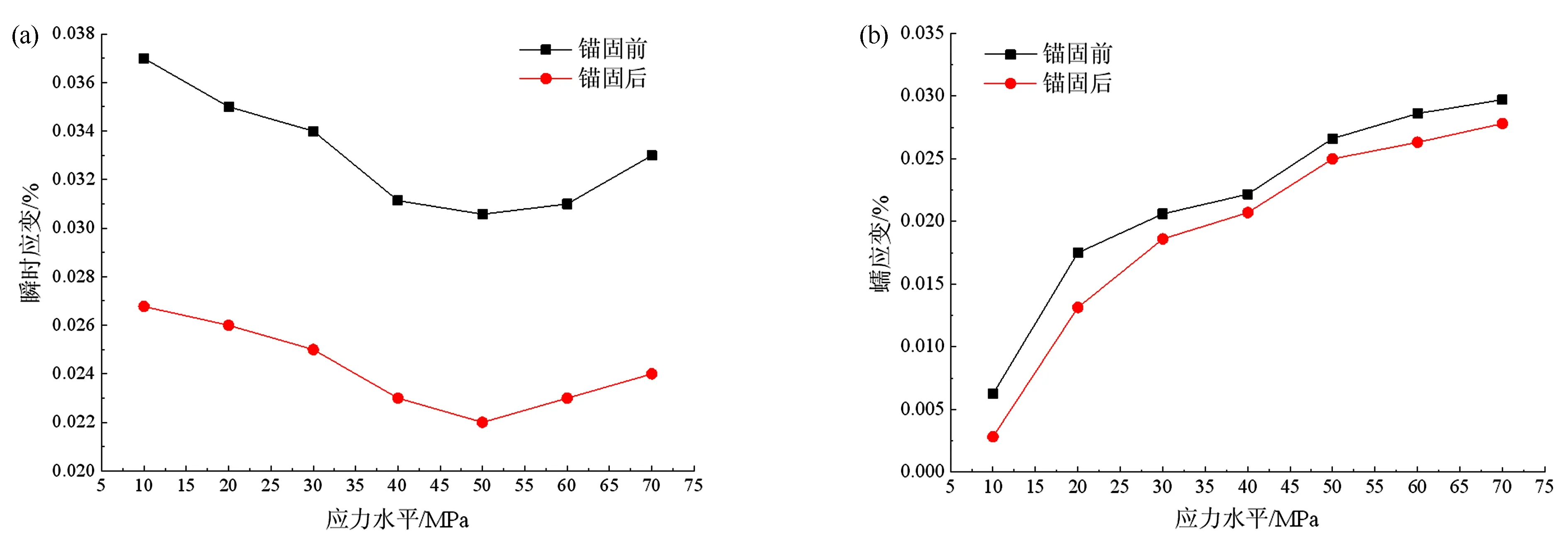
圖3 軸向應變與應力水平之間關系

對于軸向變形，當應力水平為10 MPa時，錨固前試樣的瞬時應變為0.037%，錨固后試樣的瞬時應變為0.027%；當應力水平升高至50 MPa時，錨固前試樣的瞬時應變為0.031%，錨固后試樣的瞬時應變為0.022%；應力水平由10 MPa提升至50 MPa，錨固前試樣的瞬時應變減小了16.21%，錨固后試樣的瞬時應變減小了18.51%；當應力水平繼續升高至70 MPa時，錨固前試樣的瞬時應變為0.033%，錨固后試樣的瞬時應變為0.024%，與應力水平50 MPa相比，錨固前試樣的瞬時應變增大了6.45%，錨固后試樣的瞬時應變增大了9.09%。產生上述現象的原因可能是由于試樣內部含有部分微缺陷，導致加載初期試樣內部逐漸閉合，試樣的剛度得到提升，致使瞬時應變呈遞減趨勢；隨著軸向應力的繼續增大，試樣內部開始產生新的裂隙，試樣的剛度下降，瞬時應變有所提升。

徑向變形與軸向變形情況類似，不同點在于錨固前后試樣的徑向瞬時應變變化量、蠕應變變化量均大于軸向，說明錨固有效限制了巖石的徑向變形，提升了巖石抵抗徑向變形的能力。根據試驗結果，錨固前后試樣的軸向、徑向蠕變量總體上呈逐漸遞增趨勢，且錨固后試樣的徑向蠕變量整體小于錨固前的試樣，平均降低15.7%。分析錨固前后試樣的蠕變速率可知，錨固前試樣的蠕變速率明顯大于錨固后的試樣，錨固后試樣達到穩定變形的時間更短，見圖4，原因可解釋為錨桿預緊力限制了試樣的變形。

圖4 錨固前后砂巖蠕變速率曲線

綜上分析可知，無論瞬時應變還是蠕應變、軸向應變還是徑向應變，錨固后試樣的形變量均小于錨固前的試樣，尤其對于徑向變形效果更加明顯，可以認為錨桿錨固深部地下工程圍巖主要限制圍巖的徑向變形與瞬時變形。

根據圖2不同應力水平的蠕變曲線可知，本文錨固前后砂巖的蠕變曲線表現為兩階段蠕變特征，即衰減蠕變和穩定蠕變。根據經典元件模型理論可知，Burgers模型能夠較為準確地對巖石類材料的衰減蠕變階段和穩定蠕變階段進行描述，Burgers模型一維蠕變方程可由下式表示：

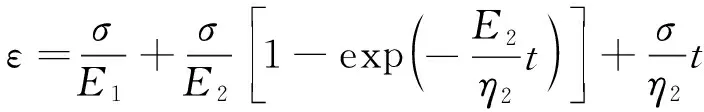
(1)

式中：σ為應力；ε為應變；E1為瞬時彈性模量；E2為黏彈性模量；η1、η2為材料的黏性系數；t為時間。

為了對比錨固前后模型參數的變化規律，采用Origin軟件對本文錨固前后砂巖蠕變曲線進行最小二乘擬合，應力水平30、40和50 MPa下參數擬合結果見表2。

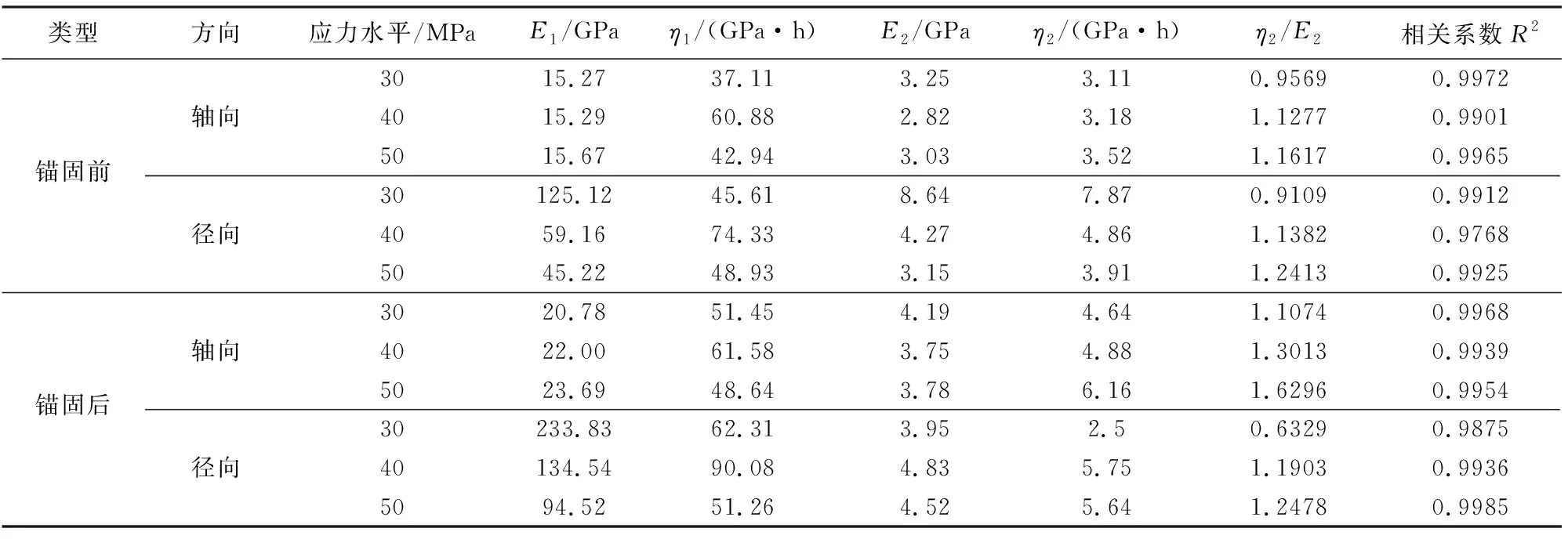
表2 Burgers模型擬合參數結果

由表2可知，錨固前后砂巖的蠕變曲線擬合相關系數均在0.95以上，說明Burgers模型能夠較好地描述錨固前后砂巖的蠕變變形行為，不同點在于參數值大小有所差異，具體如下：

(1)不同應力水平下，錨固后試樣的軸向、徑向瞬時彈性模量均大于錨固前的試樣，且徑向差值較大，說明錨桿對巖石的瞬時彈性模量，特別是徑向彈性模量影響顯著，錨固的布設有效降低了巖石的瞬時變形。從表中還可以看出，錨固前后砂巖的軸向瞬時彈性模量隨應力水平逐漸遞增，而徑向瞬時彈性模量則隨應力水平呈逐漸遞減趨勢。

(2)同一應力水平下，錨固后試樣的黏性系數η1均大于錨固前試樣，表明黏性系數η1受錨桿影響顯著，充分反應了錨桿能夠有效降低巖石的蠕變速率；從表中還可以看出，隨著應力水平的逐漸增大，黏性系數η1表現為先增再減的變化趨勢，由于巖石的蠕變硬化及損傷的綜合作用，當應力水平較低時，試樣在蠕變過程中逐漸硬化，黏性降低，進而導致黏性系數上升；當應力水平較高時，試樣內部損傷逐漸增大，黏性上升，進而導致黏性系數減小，整體上表現為非線性蠕變。

(3)隨著應力水平的升高，η2/E2逐漸增大，試樣進入穩定蠕變的時間延長。對比錨固前后砂巖的η2/E2值發現，二者之間未表現出明顯的變化規律。

3 結論

(1)相同應力水平下，錨固后砂巖的軸向、徑向變形量均小于錨固前，且錨固對于徑向變形的敏感性更大；

(2)錨固前后砂巖的軸向、徑向瞬時應變均隨應力水平的升高呈先減后增的變化趨勢，蠕應變則呈逐漸遞增變化趨勢。不同應力水平下，錨固后試樣的瞬時應變和蠕應變均小于錨固前。

(3)不同應力水平下，錨固后砂巖的軸向、徑向瞬時彈性模量均大于錨固前；相同應力水平下，錨固后砂巖的黏性系數η1均大于錨固前；隨著應力水平的升高，η2/E2逐漸增大，試樣進入穩定蠕變的時間逐漸延長。