伯努利方程教學設計中的若干問題1)

易文彬 孟慶昌 鄧 輝 王 沖 張志宏 顧建農

(海軍工程大學基礎部，武漢 430033)

伯努利方程是流體力學課程教學中的重要內容。在教學設計中常包含實驗演示、方程推導、物理意義討論、相關知識點的聯系拓展等環節。然而在教學實施的過程中，常常出現以下幾方面問題，如演示實驗解釋不合理，學生對方程推導及方程中壓強項的物理意義理解感到困惑，對方程的理解過于片面，不能建立知識點線面的聯系。針對以上問題，本文梳理伯努利方程演示實驗中的常見誤解，分析伯努利方程不同的推導方法，討論方程中壓強項的物理意義，并將伯努利方程進一步聯系拓展，以加深學生對內容的理解認識，建立科學嚴謹的分析方法。

1 演示實驗中的若干誤解

在課程內容引入時，教師往往通過一些簡易的演示實驗來激發學生興趣，然而對演示實驗的解釋往往一筆帶過，甚至忽略了方程使用的限制條件，給出錯誤的解釋，反而不利于學生科學嚴謹地分析問題。

吹紙片實驗是早期課本常用的一個演示實驗(圖1)。捏住紙片的一端，用嘴或者吹風機對著紙片的上方吹氣時，紙片則向上抬起。由于觀察到紙片上方的氣流速度快，壓強低，學生很容易誤認為是伯努利方程的原因。事實上，紙片上方和下方的流體并不處于同一流線，且初始時二者機械能也不相等(上方吹出氣流的機械能大于下方氣流的機械能)，不滿足伯努利方程的適用條件[1]。

圖1 吹紙片實驗

由實驗測量可知射流的壓強與周圍環境壓強基本相等，吹出的氣流壓強和周圍大氣壓差別不大。吹紙片實驗中紙片之所以向上抬起主要與流體黏性導致的康恩達效應以及紙片初始彎曲弧度有關[2-3]。流體流過彎曲的壁面時，因為黏性的作用，射流帶走周圍的流體向下游流動，導致附近壓強降低從而射流向壁面偏轉。根據力作用的相互性，壁面也受到指向射流方向的力，因此紙片會向射流方向抬起。射流沿著平直的壁面流動時，康恩達效應不明顯。如果紙條自然下垂，并沒有形成弧度，此時向下吹氣，則紙片擺動幅度較小，且不會出現方向性。

圖2 所示的氣頂球實驗是一個較為有趣的演示實驗：實驗時吹風機向上吹氣保持小球懸浮于吹風機上方，當水平移動吹風機時，小球也會隨之水平移動，甚至吹風機傾斜一定的角度，上方懸浮的小球也隨之移動而并不落下。文獻[4-5] 對該實驗進行了討論，但是關于氣頂球實驗的解釋爭議較大。

圖2 氣頂球實驗

為了解釋氣頂球實驗現象，本文基于CFD 軟件進行了數值模擬。計算中的小球為標準的乒乓球，直徑為0.04 m，重量為2.7 g，距離下方射流出口0.3 m。計算可得射流出流速度為12.7 m/s 時，小球可保持平衡。圖3 為射流正對球心時的流場的速度分布。觀察小球下方射流速度分布：由于黏性的作用，射流帶動周圍靜止的空氣，同時射流核心區變細。圖4 為射流正對球心時流場的壓強分布，雖然射流和周圍空氣流速差別較大，但是壓強差別較小。

圖3 射流正對球心時流場的速度分布

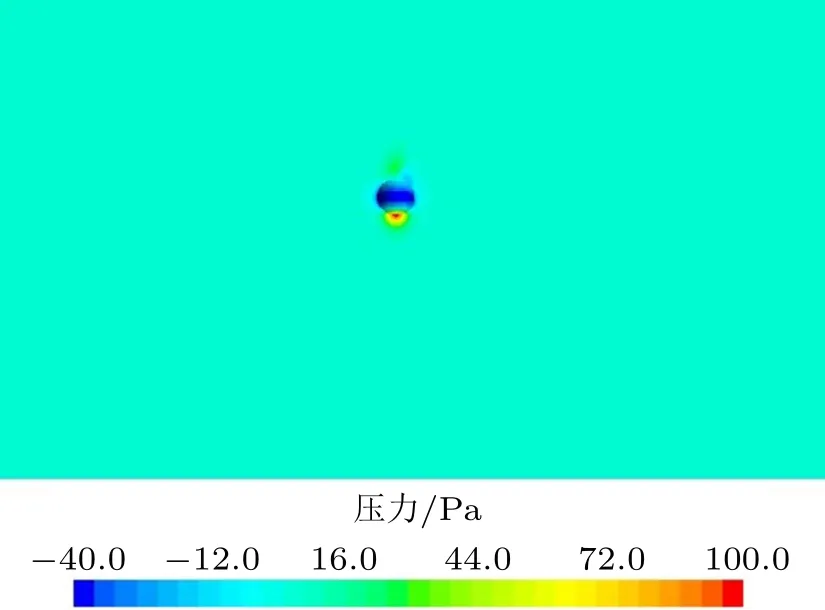
圖4 射流正對球心時流場的壓強分布

圖5 為射流正對小球左側時的速度分布，圖6為小球表面的壓強分布。小球左下方為駐點，受射流的沖擊作用為高壓區；小球左側流速較大，由流線伯努利方程可知，此處為低壓區。計算得到小球受到水平方向的合力向左，為5.5 mN，相當于0.2 倍小球的重量，此力拉動小球向左移動。其中一種解釋為康恩達效應導致小球左側壓強降低，進而產生水平的作用力，同時壓強降低會出現流線彎曲且流動加速的現象[6]。

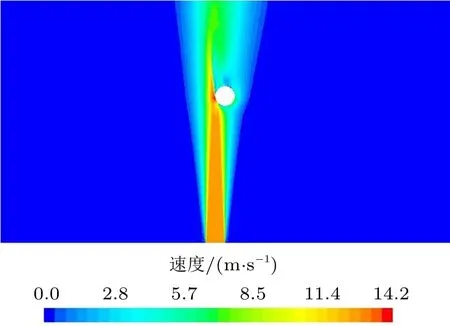
圖5 射流正對小球左側時流場的速度分布

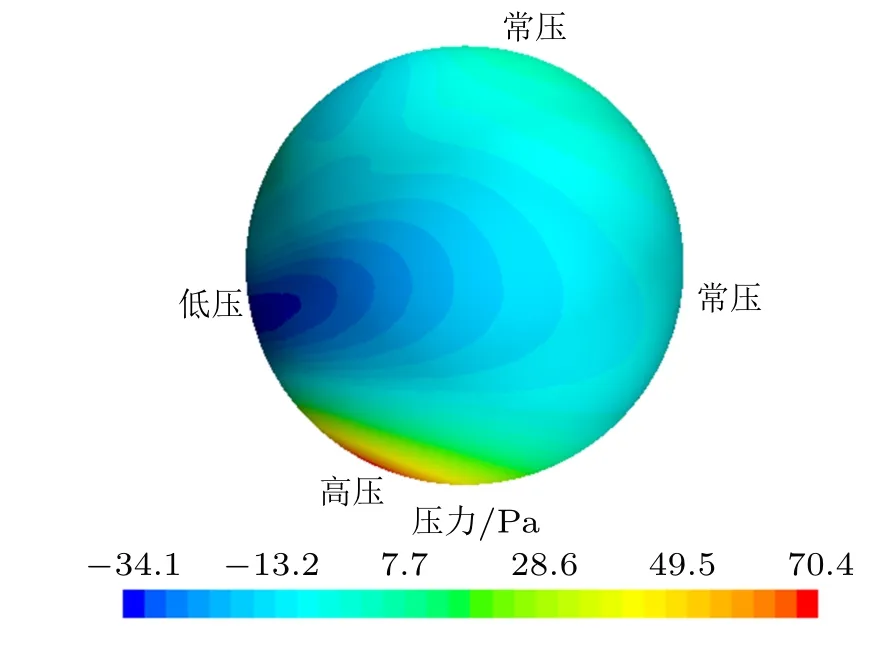
圖6 射流正對小球左側時小球的壓強分布

2 伯努利方程的推導及物理意義

不同流體力學教材中關于伯努利方程的推導有不同的方法。有的是基于理想流體運動微分方程(歐拉方程或蘭姆方程)沿流線積分得到，有的是基于功能原理推導。不同的推導過程難易不同，學習了解多種推導方法有助于學生加深對伯努利方程的認識理解。

2.1 推導方法一

在定常流場中，基于牛頓第二定律分析理想流體微元體的受力，可得到歐拉運動微分方程為

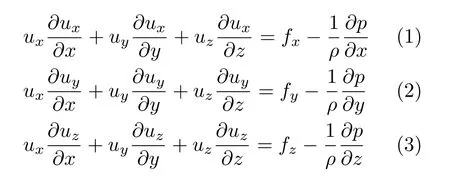
式中，p為流體的壓強；ux，uy，uz分別為速度u沿坐標軸x，y，z三個方向上的分量；fx，fy，fz分別為單位質量流體的質量力f沿x，y，z三個方向上的分量，z軸垂直向上。

將方程(1)～(3) 沿流線積分即可得到伯努利方程[7]。由流線方程

可得到uydx=uxdy，uzdx=uxdz，所以式(1)乘以dx后可寫為

式中，u2/(2g) 為單位重量流體的動能，z為單位重量流體的重力勢能，p/(ρg) 為壓力對單位重量流體所做的功。理想流體沿著流線定常流動時，單位重量流體的動能、勢能和壓力做功之和為常數。這三種形式的能量和功在流動的過程中是可以轉化的，伯努利方程是能量轉化與守恒定律在流體力學中的具體反映[7]。

此外，也可以根據蘭姆運動微分方程進行推導[8]。蘭姆運動微分方程為歐拉運動微分方程的另外一種表達形式，優點是對于無旋流動時，方程可以大大簡化，此處不再贅述。

2.2 推導方法二

在理想流體的定常流動中，考慮沿流線方向作用于流管中一個微元上的力，并對此微元應用牛頓第二定律(圖7)。垂直于流線的此微元截面積具有任意的形狀，其面積大小由dA變化為dA+o(dA)。忽略二階小量后，微元的質量為

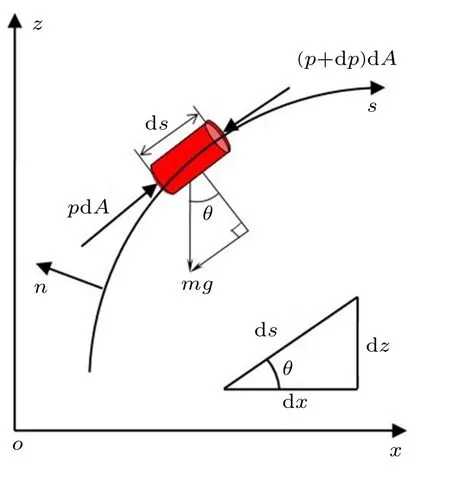
圖7 沿流線運動的微元

沿流線切線方向進行受力分析，理想流體無切應力，則表面力為

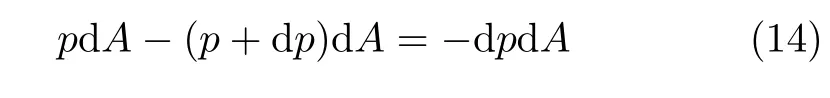
重力場中，重力在流動方向上分量為

式(17)與式(10)相同，適用于可壓流體和不可壓縮流體。在不可壓縮條件下積分即可得到常見形式的伯努利方程。式(17) 通常也稱為一維歐拉方程，是列奧納德·歐拉(Leonhard Euler) 于1750 年首先導出。此方法的優點在于學生未掌握歐拉運動微分方程時也能夠較好理解伯努利方程的推導過程。

2.3 推導方法三

在理想流體定常流動中，任取一微流束，取1-2 段作為控制體進行分析(圖8)。假設在t時刻，流體系統與控制體重合，在t+ dt時刻，流體系統運動至1′-2′位置。微流束在過流斷面1-1和2-2 處的面積，壓強，流速，密度，高度分別為dA1，dA2，p1，p2，u1，u2，ρ1，ρ2，z1，z2。對不可壓縮流體，ρ1=ρ2。

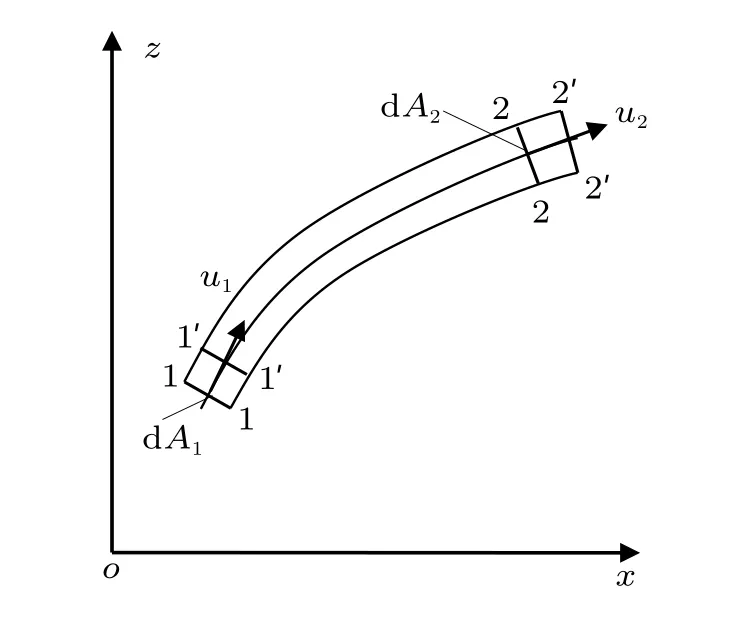
圖8 定常流場中的微流束

由定常不可壓縮條件知，微流束在1-1′和2-2′段的體積相等，用dV表示。忽略二階小量，流體從1-2 移動到1′-2′外界壓力對系統做功

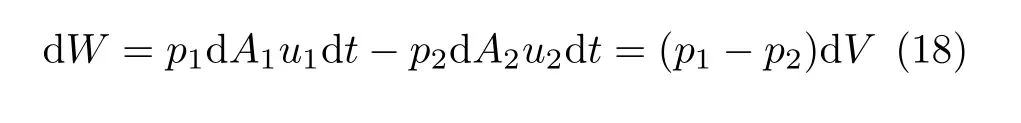
流體從1-2 段運動到1′-2′位置時機械能的增量

與前兩種推導方法不同，方法3 是基于功能原理推導得到。方法3 比較簡潔直觀，適合基礎比較薄弱的學生掌握。

2.4 伯努利方程中壓強的物理意義

由以上推導過程可知，伯努利方程中z代表了重力對單位重量流體所做的功，表示單位重量流體的重力勢能。p/(ρg) 代表了壓力對單位重量流體所做的功，為方便理解，部分中文教材也稱之為單位重量流體的壓強勢能(簡稱壓能)，屬于一種機械能。學生在課堂學習時可能遇到以下困惑：壓強是一種勢能嗎？固體有沒有壓強勢能？

為避免學生產生困惑，大多數英文教材中關于伯努利方程中壓強項的物理意義并未過多解讀[9]。教材[10]將伯努利方程(12)左邊三項分別稱為單位重量流體的動能，勢能和可逆的壓強功。教材[11] 中將壓強項稱為壓頭，且指出一般不稱其為壓力能。流體中存在壓力做功，這是由于流體在壓力作用下可以流動做功，它是流體中一種特殊的能量，固體則沒有這種特性。此外，某一空間點處單位重量流體的壓能容易求得(不可壓縮條件下為p/(ρg))，但對于一個系統中的壓能通常難以積分求得，這也限制了將壓強項作為一種能量來處理應用，因此在推導方法3 中將壓強影響作為力而非能量來考慮。

3 伯努利方程的聯系與拓展

伯努利方程與流體力學課程中的其他內容有著密切的聯系(圖9)。如流體靜止時，伯努利方程退化為靜力學基本方程；考慮黏性流體管內流動損失時，可以建立黏性總流伯努利方程。如果在課程中引導學生建立點線面的知識體系將有助于加深學生對整個課程的理解和認識。

圖9 伯努利方程的知識聯系

文獻[12] 闡述了伯努利方程在流體靜力學、定常孔口出流、畢托管測速、文丘里管流量和翼型繞流等具體流動中的成功應用。公元前250 年，阿基米德提出了流體力學浮力定理。而流體靜力學基本方程正是伯努利方程在速度為0 時的特殊形式。1653年，帕斯卡發現的流體壓強傳遞特性也是伯努利方程的一個特殊形式。1643 年，意大利科學家托里拆利通過實驗的方法總結出了定常孔口出流的基本公式。流體質點從自由液面運動到孔口，重力勢能轉化為動能，其機械能守恒的思想與伯努利方程不謀而合。利用伯努利方程的原理還可以通過畢托管測速或文丘里管測流量。值得注意的是，畢托管測速儀的發明時間早于伯努利方程的提出時間，而文丘里流量計發明時間明顯晚于伯努利方程的提出時間。從中我們可以看到，實驗和理論分析是科學研究的兩個重要方法，且相輔相成，相互促進。知識的發現并非一蹴而就，各知識之間蘊含著豐富的聯系。

伯努利方程可以在定常、沿流線、無黏、不可壓縮、重力場的條件下推導得出。若流線上兩點高度相等或者重力可忽略時，伯努利方程也可以寫為

對于理想氣體做絕熱連續流動，考慮氣體的壓縮性，結合完全氣體狀態方程式(23)，等熵壓縮關系式(24)，焓的定義式(25) 對歐拉運動微分方程沿流線積分可得到可壓縮等熵氣流的伯努利方程。

式中，c∞為來流聲速，p∞，ρ∞，u∞分別為來流靜壓，密度和速度。引入馬赫數Ma∞=u∞/c∞，當Ma∞＜0.3 時，一般認為流體壓縮性引起的總壓變化可以忽略不計。

4 小結

伯努利方程形式簡單，在實際工程中有著廣泛的應用，是流體力學課程教學中的重點和難點。圍繞伯努利方程的教學設計需要注意以下幾個方面的問題。

(1) 關于演示實驗的解讀應該做到深入且嚴謹，應當注意到伯努利方程的適用條件，綜合考慮流體黏性，抽吸，康恩達效應等因素的影響。

(2)方程的不同推導方法難易不同，出發的角度不同。了解方程的不同推導方法有助于加深學生對伯努利方程本質的理解認識。

(3)流體力學中文教材中多將伯努利方程中壓強項解讀為壓強勢能，而英文教材多沒有這種說法。伯努利方程中壓強項的本質是壓力對單位重量流體所做的功，在流體當中，它可作為一種特殊的能量，稱之為壓能。但是流體系統的壓能難以積分求得，且在固體中并不存在這種能量，為避免學生產生困惑，也可不將其解讀為壓能。

(4)伯努利方程與流體靜力學等知識點有著豐富的聯系，適當的聯系拓展有助于學生體會知識的發現過程，加深對流體力學研究方法的認識。

(5)在可壓縮條件下，伯努利方程的形式及物理意義均有所改變，學生應仔細對比鑒別。