含阻尼多裂紋Euler–Bernoulli 曲梁強迫振動的Green 函數解1)

趙 翔 李思誼 李映輝

*(西南石油大學土木工程與測繪學院，成都 610500)

?(西南交通大學力學與工程學院，成都 610500)

近年來，曲梁憑借著承載力高，造型獨特等特點廣泛應用于現代結構工程中[1-2]，例如渦輪等高速機械構件、飛機機身、潛艇與艦船的外殼以及許多輕型的結構和橋梁[3]。Fu 等[4]提出了由曲梁單元組成的網格結構的設計策略，為機械超材料開發提供了理論依據。Huang 等[5-6]對復合材料薄壁曲梁的穩定性進行了分析，并考慮彈性約束的邊界條件，分析了復合材料層合曲梁的非線性穩定性。曲梁的振動分析一直是國內外研究的熱點問題。Chidamparam 等[7]研究了預應力靜力平衡狀態下平面曲梁、圓環和拱的自由振動問題。Riedel 等[8]研究了中間彈性支承的雙跨Euler–Bernoulli 曲梁的自由振動響應。趙翔等[9]運用Laplace 變換法，研究了Timoshenko 曲梁在強迫振動下的Green 函數。何燕麗等[10]運用Green 函數法求解了曲梁壓電浮能器Prescott 模型的Green 函數解。此外，有限元法[11-13]在研究曲梁動力分析中也被廣泛采用。

梁構件的損傷問題在實際工程中普遍存在，梁結構通常帶裂紋工作[11]。裂紋的存在會降低結構的剛度，從而影響結構的動力特性(固有頻率、振型和阻尼比)[14-15]。因此，研究帶裂紋曲梁在外激勵作用下的動力特性具有實際意義。目前針對多裂紋Euler–Bernoulli 曲梁(Euler–Bernoulli curved beam，ECB) 強迫振動問題的研究還較少，多數是對含裂紋的直梁振動的研究。Ghondos 等[16]針對含開口裂紋的Euler–Bernoulli 梁的橫向振動問題，建立了連續裂紋梁振動理論。Caddemi 等[17-18]求解了含多個集中裂紋Euler–Bernoulli 梁和柱的精確的閉式解。Zhao 等[19]利用裂紋截面的不連續斜率模型和Abu-Hilal[20]的工作，給出了Euler–Bernoulli 梁強迫振動下的格林函數解。Chen 等[21]得到了具有阻尼效應的多裂紋Timoshenko 梁強迫振動的閉式解。

經調研發現，對多裂紋曲梁強迫振動問題的研究十分有限。因此，本文給出了多裂紋ECB 的強迫振動的精確閉式解。根據裂紋截面位置的連續性條件[22]以及Zhao 等[19]和Chen 等[21]的工作建立多裂紋ECB 的Green 函數表達式，式中的未知常數由邊界條件確定。驗證研究結果的有效性，討論一些幾何物理量的影響。

1 具有阻尼效應的ECB 強迫振動的Green函數

本文研究了半徑為常數的多裂紋Euler–Bernoulli 曲梁振動模型，如圖1 所示，不考慮轉動慣量和剪切變形。梁高h，梁寬b的曲梁梁長為L，半徑為R，在x=x0處受到簡諧集中力P0eiΩt的作用。假設曲梁模型上存在n個開口裂紋，將曲梁分成了長度為Li(i=1，2，...，n+1) 的n+1 個完整段，根據文獻[19] 中提出的坐標系建立方法，在多裂紋ECB 模型中建立n+1 個局部坐標系oixiyi(i=1，2，...，n+1)。另外，采用等效無質量扭轉彈簧模型來描述曲梁裂紋位置的力學行為。圖1 中，Ji(i=1，2，...，n) 表示第i個裂紋處的等效扭轉彈簧的局部柔度，是彈簧剛度Keq的倒數，可表示為

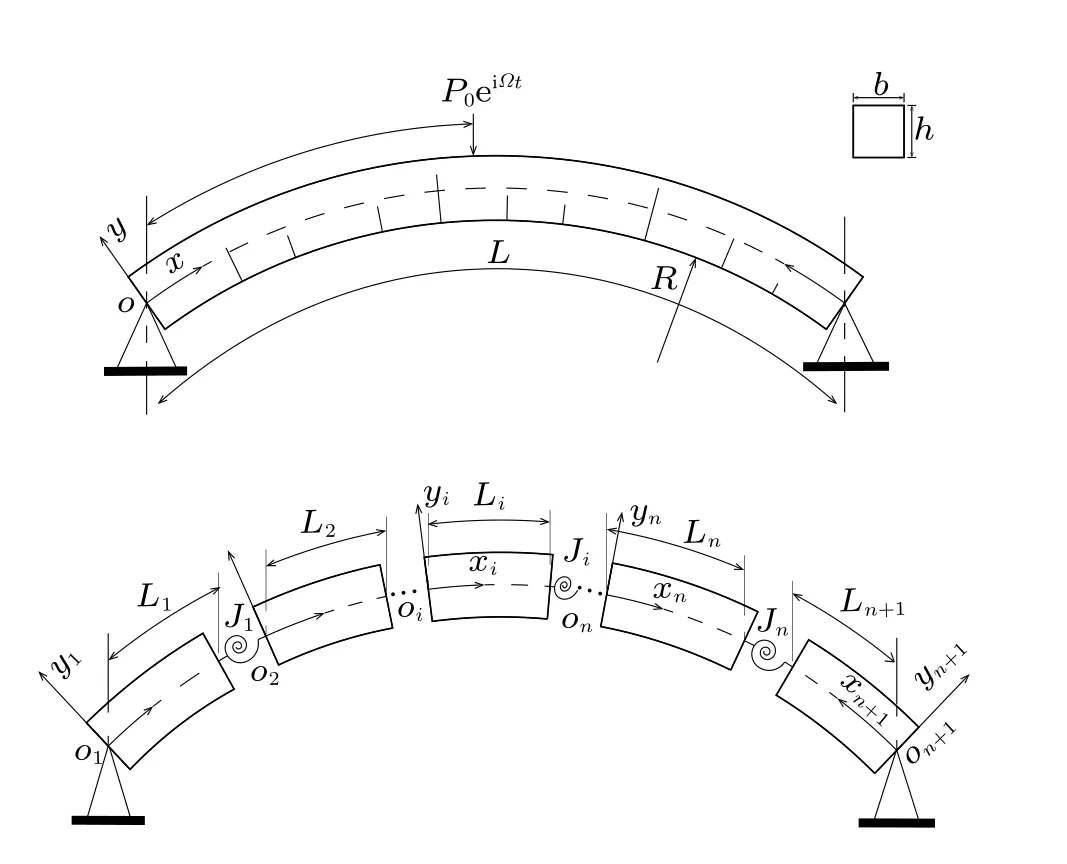
圖1 含n 個裂紋的兩端簡支ECB 在x=x0 處受到簡諧力P0eiΩt 作用

其中h′=hc/h是裂紋深度與曲梁高度的比值。

在考慮裂紋影響之前，首先要求解出ECB 強迫振動的Green 函數。根據趙翔等[9]的研究，已經系統地求解出了Timoshenko 曲梁在強迫振動下的穩態Green 函數解。本文在此基礎上得到了強迫振動ECB 的Green 函數解。在此對其過程做簡單說明。

引入ECB 控制方程[9]

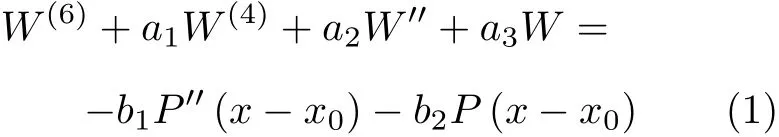
式中W(x)是曲梁的徑向位移，W′′，W(4)，W(6)是徑向位移的各階導數，P(x) 是曲梁受到的簡諧作用力，常數ai(i=1，2，3)，bi(i=1，2) 分別定義為[9]

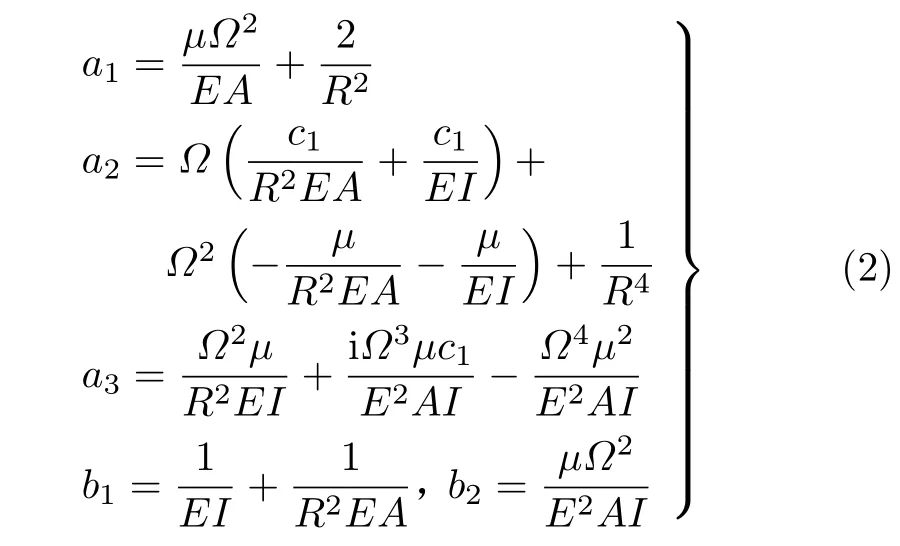
其中c1為阻尼系數，μ是單位長度質量，Ω是外激勵頻率，A是曲梁橫截面面積，E是彈性模量，EI表示抗彎剛度，EA是抗拉剛度。

ECB 的Green 函數G(x;x0) 是指曲梁在x0處受到單位集中力時穩態響應的撓度，是式(3) 的解

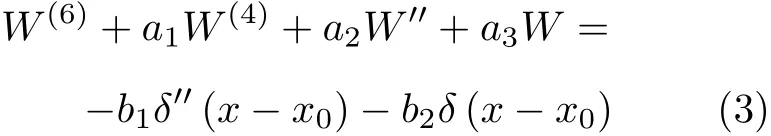
式中δ(·) 是狄拉克函數。

通過疊加原理和Laplace 變換可以得到Green函數

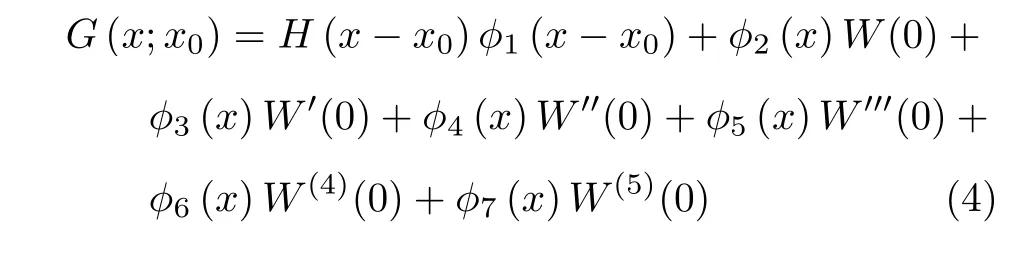
其中，未知常數W(0)，W′(0)，W′′(0)，W′′′(0)，W(4)(0)，W(5)(0) 分別為W(x) 在x= 0 處的各階導數，可以由曲梁兩端的邊界條件確定；H(·)是單位越階函數；φi(x) (i= 1，2，···，7) 與Ai(x)(i=1，2，···，6) 定義為

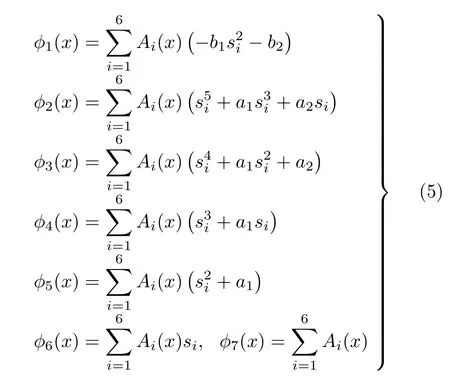
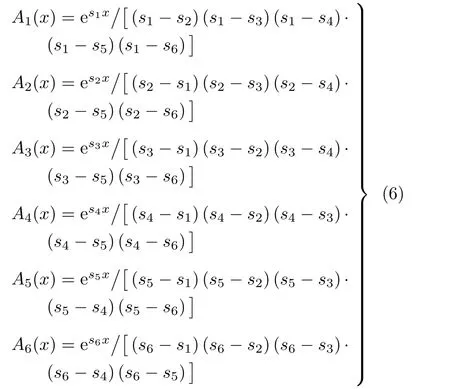
si(x)(i=1，2，···，6) 是式(7) 有關頻率Ω的代數方程的根

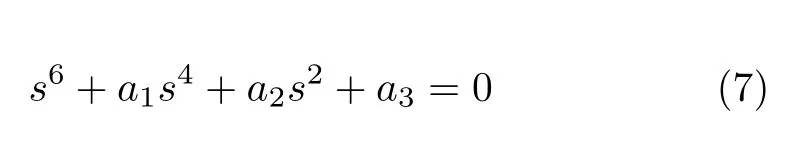
曲梁的動力學分析要比直梁模型復雜很多，需要考慮曲梁的軸向位移、徑向位移以及耦合位移等。因此為了研究裂紋曲梁的力學行為，還需要求解出軸向位移V(x) 的Green 函數。Green 函數為

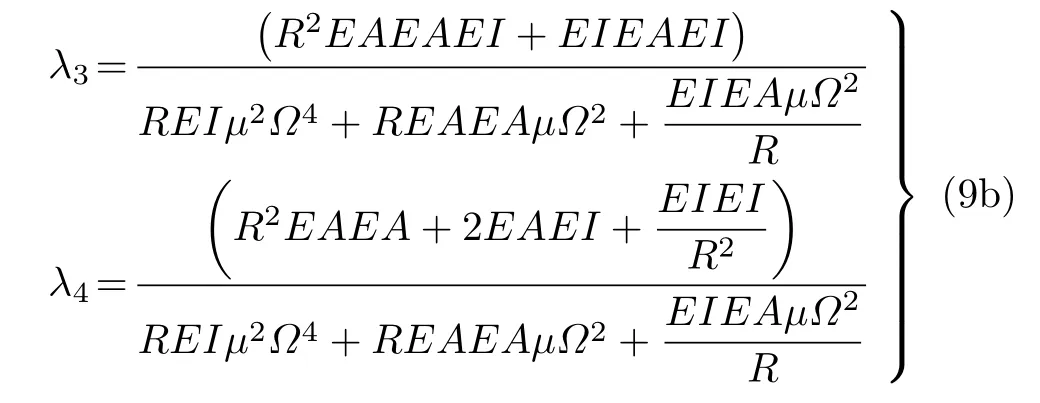
比較式(4)和式(8)發現，軸向位移和徑向位移的格林函數的數學形式相同，所含的未知常數也相同，并且這些常數都與零點有關，可以利用這一特征簡化計算過程。

2 多裂紋ECB 的Green 函數解

兩端簡支的曲梁邊界條件(軸向位移與徑向位移為零，彎矩為零)[22]可以確定位移和力學邊界:W1(0) = 0，V1(0) = 0，W′′1(0) = 0，Wn+1(0) =0，Vn+1(0)=0，W′′n+1(0)=0。

局部坐標系下的Green 函數 ˉGi(xi;xi0) (i=1，2，···，n+1) 表達式為

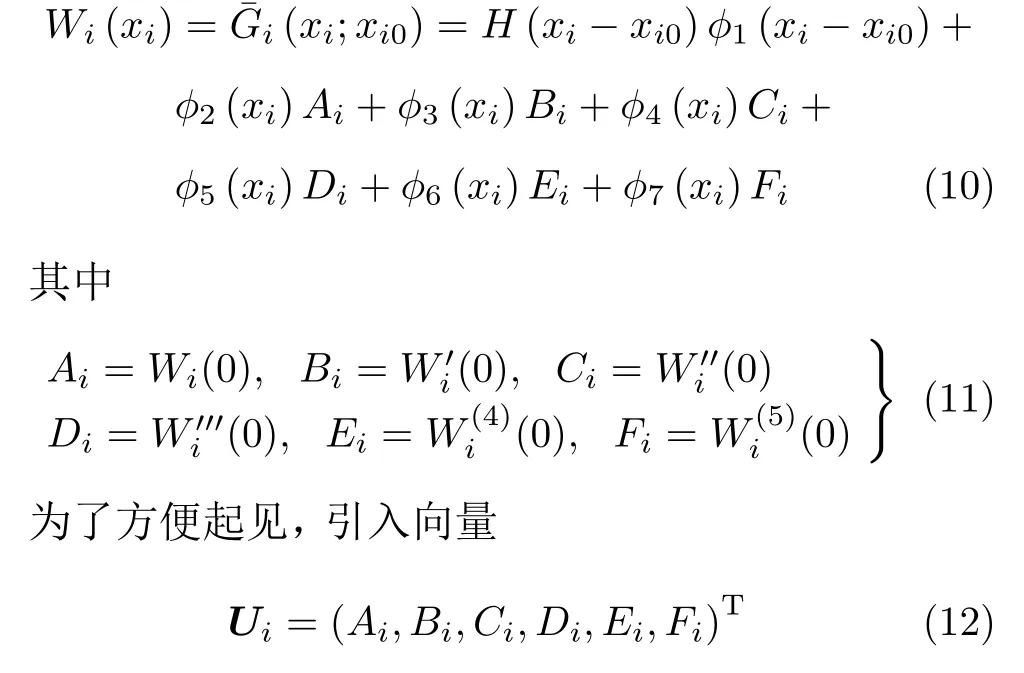
2.1 裂紋截面處的轉換關系

其中F(x)，M(x)，Q(x) 是曲梁的軸力、彎矩以及剪力，θ(x) 是截面轉角，分別為

由式(15) 可知，在第i(1 ≤i ＜n) 裂紋截面處的轉移關系可由式(17) 獲得

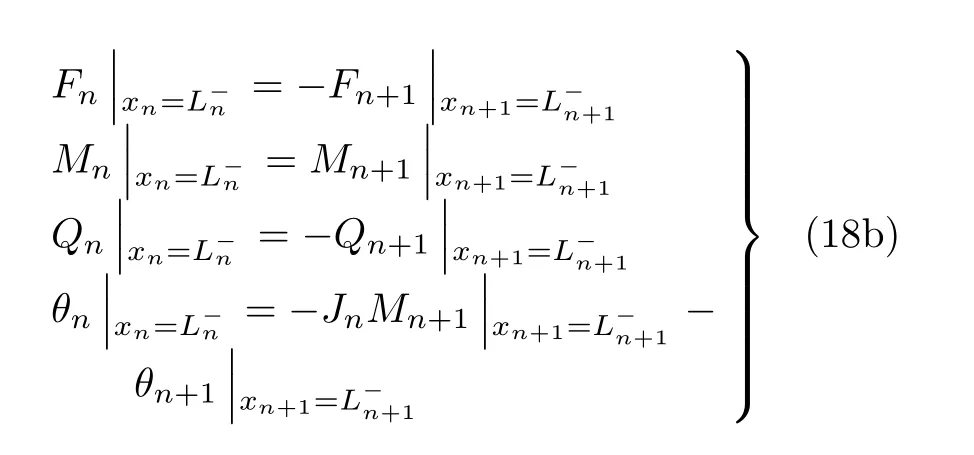
將式(10) 代入式(18) 得到

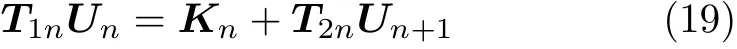
其中

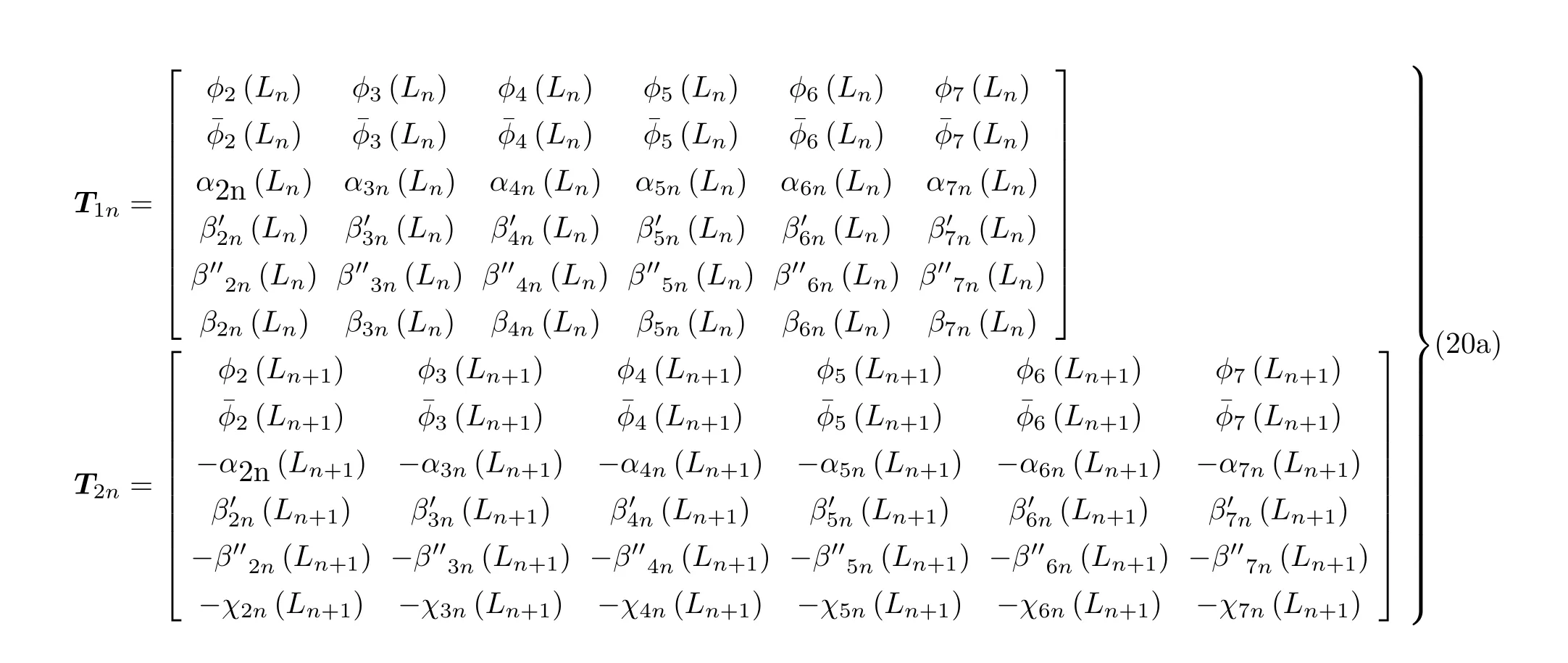
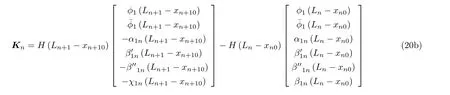
另外

2.2 確定未知常數

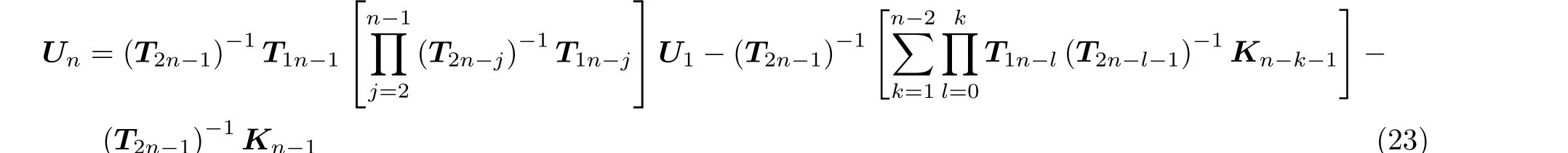
ECB 被裂紋分成的每一段都有6 個未知常數，共有6n+6 個未知常數需要定義。曲梁在左端x=0處的邊界條件可以把第1 段的6 個未知常數減少至3 個，同樣在右端x=L處的邊界條件可以把第n+1段的未知常數減少到3 個。最后由轉換關系式(17)和式(21) 確定其余常數，從而得到一個只含有6 個未知常數的方程。

裂紋曲梁第1 段和第n+1 段的未知向量為

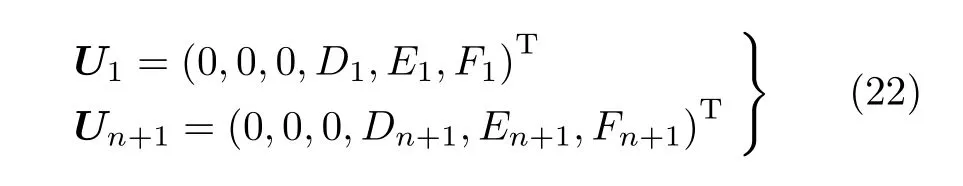
由式(17) 可知，U1和Un的關系為

將式(23) 代入式(21) 得到

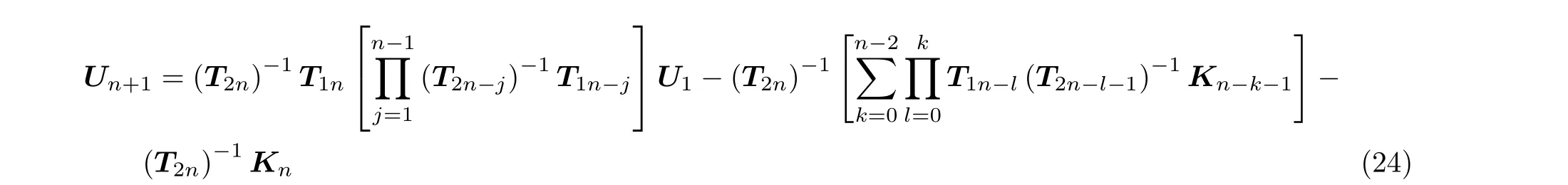
式(24) 已經完成了減少變量的過程，是只有六個未知常數D1，E1，F1，Dn+1，En+1，Fn+1的方程，其余向量Ui(i=2，3，···，n)可通過式(17)定義。另外推導出含n個裂紋曲梁的頻率方程，如式(25)

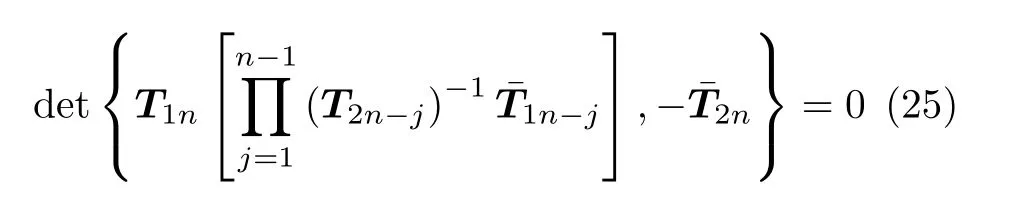
其中

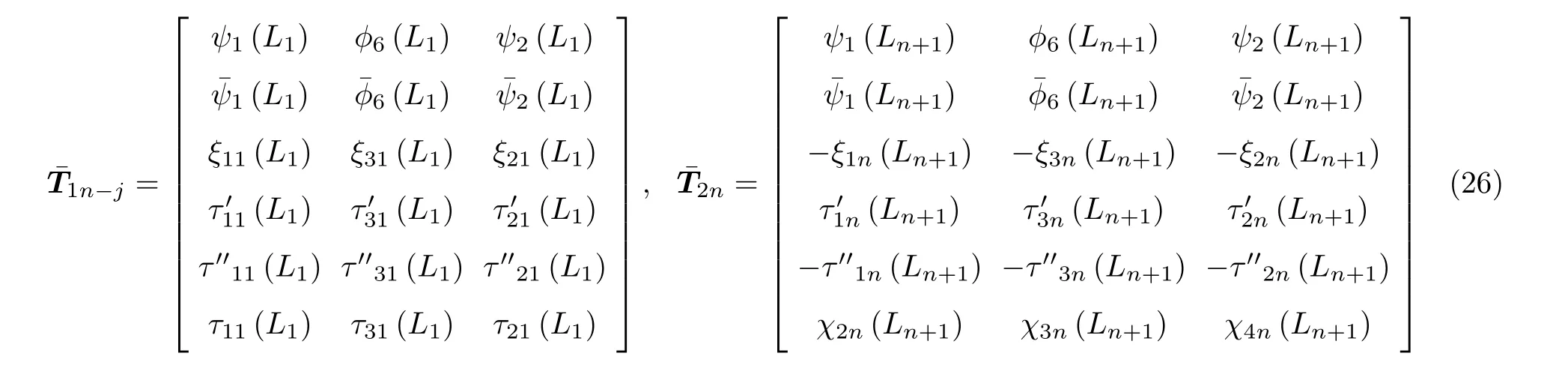
式中，

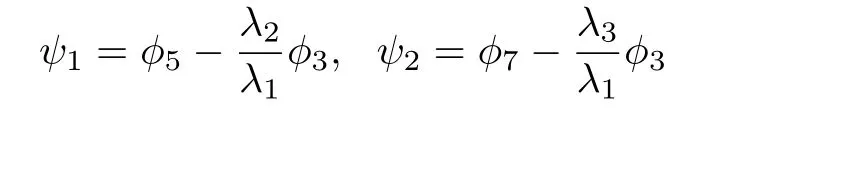
2.3 坐標變換

3 數值結果與討論

在本節中，考慮一個兩端簡支的ECB，在x=2/L處受到單位簡諧集中力作用。為了方便起見，引入無量綱化參數

3.1 解的有效性驗證

本小節驗證了多裂紋ECB 強迫振動解析解的有效性。在上文中已經提到使半徑趨于無窮大，ECB的Green 函數解可以退化為EB 的Green 函數解，因此將本文的退化解與文獻[19] 進行對照。如圖2所示，設定相同的材料參數與裂紋參數，對照結果表明本文結果的退化解與文獻[19] 中的結果基本一致。但存在些許誤差，原因是曲梁半徑無窮大不可能真實存在，本文設置R= 10 000 m 得到的結果已經與文獻基本吻合。因此這一誤差并不影響本文解的有效性驗證。另外還建立了兩端簡支EB 的有限元模型，對比了本文的退化解與有限元算例的位移解，結果基本吻合，從而進一步驗證了解的有效性。

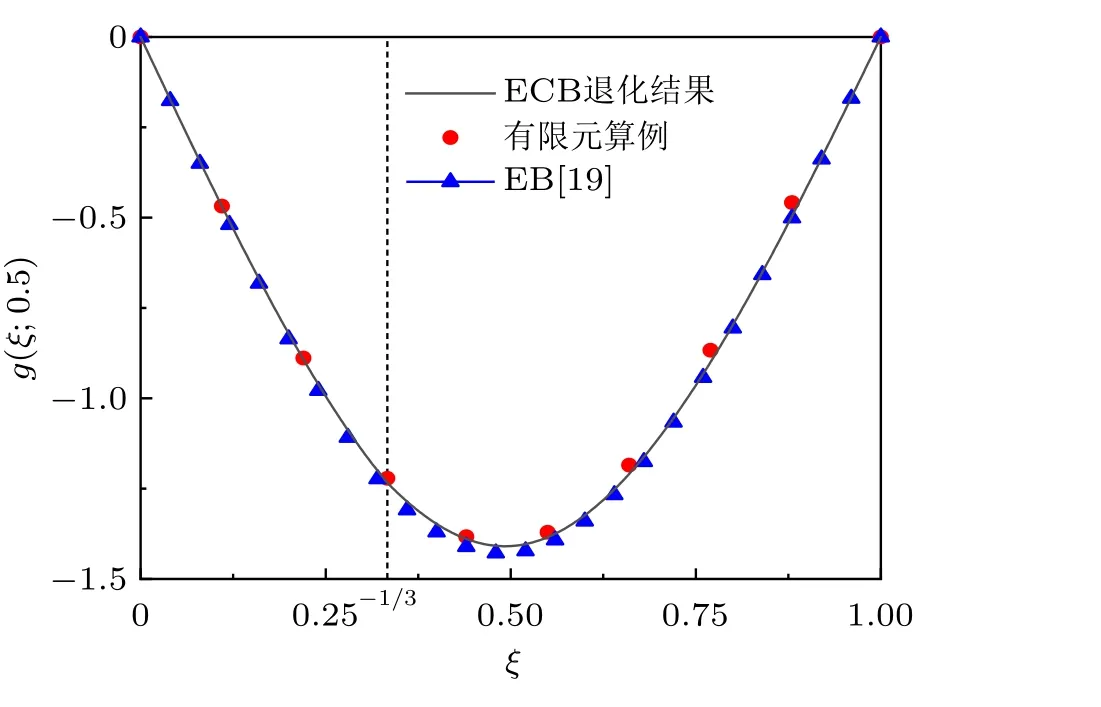
圖2 在簡諧激勵下梁穩態響應時各點簡諧運動的幅值曲線(h′ =0.2)

3.2 幾何物理參數對ECB 振動響應的影響

本節內容分別分析了裂紋深度、裂紋位置、曲梁半徑對振動響應的影響以及雙裂紋之間的相互影響。

圖3(a) 和圖3(b) 所示是以裂紋深度h′和裂紋位置L′為自變量時的無量綱化的撓度g(ξ;0.5)，其橫坐標是無量綱化的曲梁的跨度ξ，從圖中可以看出撓度隨著裂紋深度h′和位置L′的增大而增大。從物理意義看，曲梁上產生最大撓度的位置也發生了變化，如果裂紋深度較大或者裂紋位置較靠近跨中，裂紋處的撓度就會大于跨中撓度；相反，裂紋深度較小或者裂紋位置遠離跨中，曲梁的最大撓度仍在跨中產生。

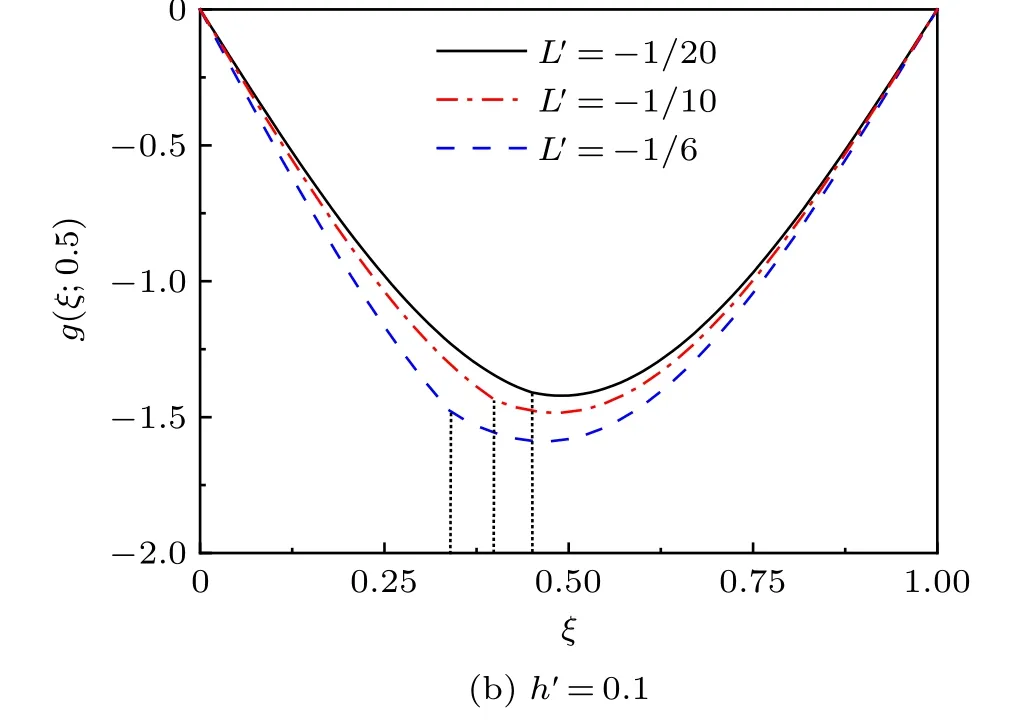
圖3 ECB 的無量綱化位移g(ξ，0.5)(R =2，垂直虛線表示裂紋位置)(續)

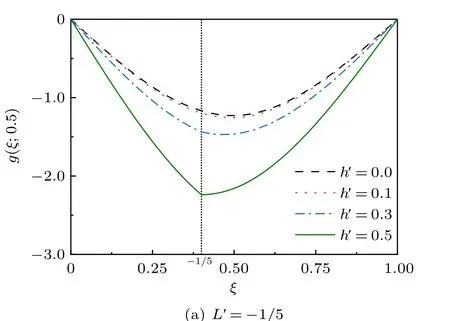
圖3 ECB 的無量綱化位移g(ξ，0.5)(R =2，垂直虛線表示裂紋位置)

圖4 是不同半徑下的ECB 無量綱化的撓度g(ξ;0.5)，其橫坐標是無量綱化的曲梁的跨度ξ。從圖中可以看出，隨著半徑的減小，ECB 的撓度逐漸減小，最大撓度也逐漸接近裂紋位置。

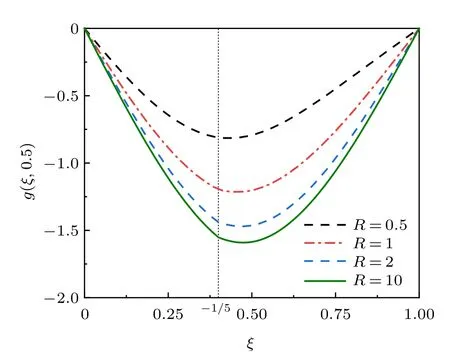
圖4 不同半徑下ECB 的無量綱化位移g(ξ;0.5) (h′ =0.3，垂直虛線表示裂紋位置)

假設兩個裂紋深度相同并且在曲梁上的位置中部對稱，可表示為±L′(0 ≤L′≤0.5)。為了研究雙裂紋曲梁中兩個裂紋之間的相互作用，引入兩個裂紋深度相同的單裂紋梁，位置表示為+L′，-L′。圖5 所示是ECB 無量綱化的撓度g(ξ;0.5)，其橫坐標是無量綱化的梁的跨度ξ。圖中填充區域的面積表示兩個裂紋之間相互作用的強度，面積越小，撓度g(ξ;0.5;±1/5) 和gsum(ξ;0.5) 之差越小，相互作用越明顯，反之亦然。

圖5 ECB 的無量綱化位移g(ξ;0.5)(h′ =0.3，垂直虛線表示裂紋位置)

4 結論

本文研究了多裂紋ECB 強迫振動的Green 函數解，適用于不同邊界條件下的ECB。數值計算中，通過將多裂紋ECB 退化解與多裂紋EB 模型文獻解和有限元算例的位移值比較，驗證了解的有效性。通過探究裂紋深度、裂紋位置、曲梁半徑對曲梁撓度的影響，得出以下結論：(1) 隨著裂紋深度和裂紋位置的增加，ECB 的無量綱撓度逐漸變大；(2) ECB 無量綱撓度隨著半徑的增加而增大；(3)以雙裂紋梁為例，研究了裂紋之間的相互作用，用響應撓度曲線之間的面積表示了相互作用的強度。文中所研究的理論公式可為相關領域的分析和計算提供理論參考。