Matlab 求解理論力學問題系列(五)不同坐標系間的數(shù)據(jù)轉換問題

高云峰

(清華大學航天航空學院， 北京 100084)

本系列文章介紹了很多利用數(shù)值計算處理問題的方法和過程。由于存在計算誤差，以及人為的輸入錯誤，計算得到的大量數(shù)據(jù)可能有誤。作為Matlab求解理論力學的系列文章，十分強調計算的可靠性，所以前面曾經(jīng)介紹過利用系統(tǒng)的守恒量來驗證數(shù)值計算的精度，或者利用解析解進行對比測試。如果系統(tǒng)不存在守恒量，可以考慮退化等特殊情況(這時往往有解析解或守恒量)，對退化情況檢驗之后，再進行后續(xù)的計算。

某些問題可能在不同的坐標系中處理更方便，那如何判斷其是否正確？本文介紹一種數(shù)據(jù)轉換的方法，可以把不同坐標系的結果轉換到希望的坐標系中來觀察，并驗證其準確性。

為此本文設計了這樣兩個問題：(1)在非慣性系中看，隨手拋出的一個物體，其軌跡很復雜，我們如何來判斷計算是正確的呢？(2)在地球某點觀察太陽，太陽的視運動軌跡是什么曲線？

1 不同坐標系中的數(shù)據(jù)轉換關系

設有矢量ρ和兩個坐標系Oxiyizi和Oxjyjzj(圖1)，基矢量分別為ei?(exi eyi ezi)T和ej?(exj eyj ezj)T。若用(ρ)i表示ρ在坐標系Oxiyizi中的分量，有

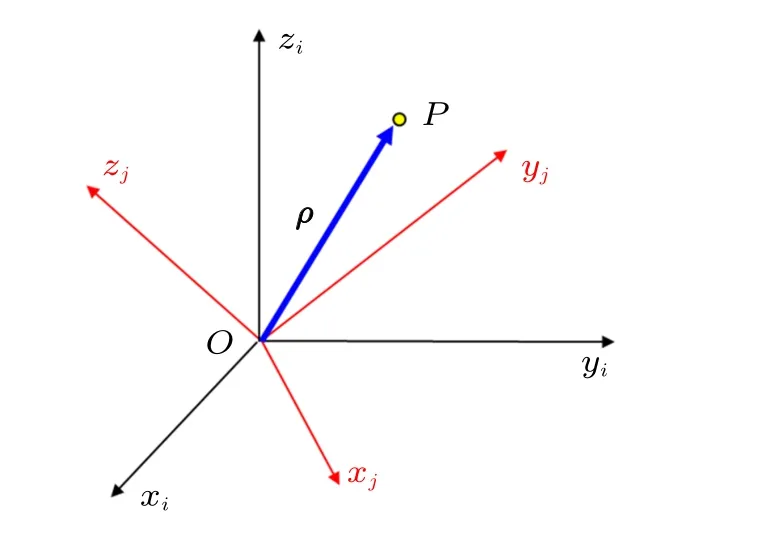
圖1 矢量和坐標系

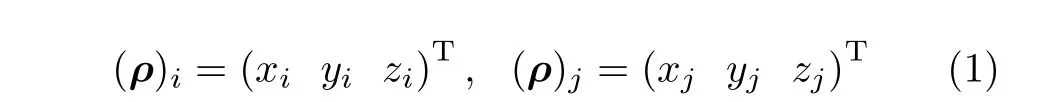
利用基矢量，矢量ρ可以表示為

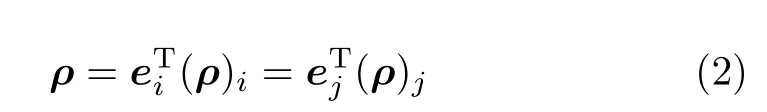
矢量與坐標系沒有關系，但是它在不同坐標系中的分量就與坐標系有關系了。因此一個問題就是：(ρ)i與(ρ)j有什么關系？

將式(2) 改寫，有

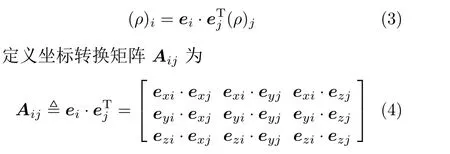
由于兩個單位矢量的點積等于其夾角的余弦，所以Aij也稱為方向余弦矩陣，從而有[1]

從式(5) 類似有(ρ)i=Aik(ρ)k，從而得到坐標系轉換矩陣的傳遞關系

以式(5)和式(6)為基礎可以得到更一般的關系。假設Ox1y1z1是基準參考坐標系(如動力學中的慣性系)，ox′y′z′是平動坐標系(坐標系始終與基準坐標系平行)，ox2y2z2是任意的動系(如動力學中的非慣性系)，ox2y2z2初始時刻與ox′y′z′重合，轉動后用三個角度(如歐拉角ψ，θ，φ) 來表示；P是動點，在基準坐標系中矢徑為R，相對運動的矢徑為ρ，動系原點的矢徑為RO(圖2)。

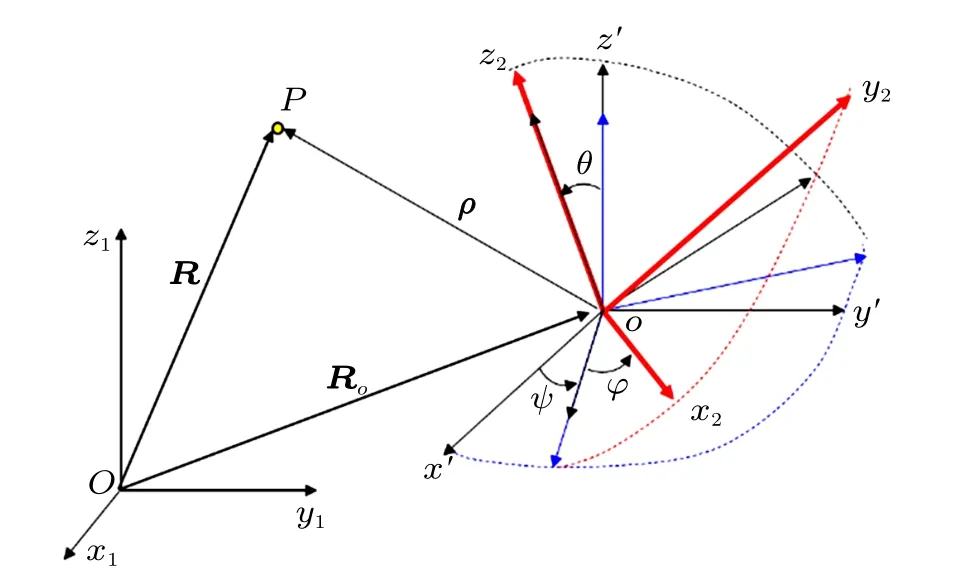
圖2 空間一般坐標系

根據(jù)運動學關系，始終有[2]

式(7) 可以在任意坐標系中表示，根據(jù)式(5)，則有

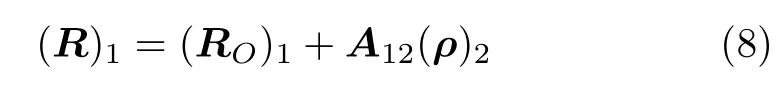
式(7) 給出了一般情況下坐標轉換關系，其中坐標轉換矩陣還是比較復雜的，如果用歐拉角表示，利用式(6) 的關系后，有

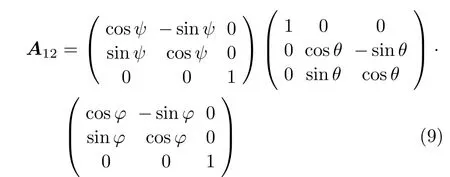
2 不同坐標系中的拋物問題

兩位觀察者，A在地面上(慣性坐標系)，B在勻速轉動的轉盤邊緣(非慣性系)。B隨手拋出一物體，求兩位觀察者看到的物體運動軌跡(圖3，不考慮空氣阻力)。

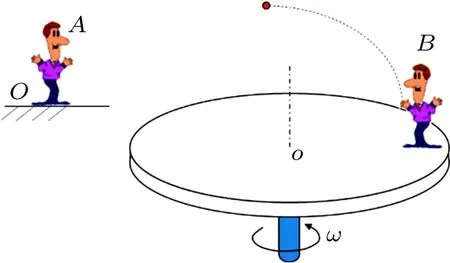
圖3 拋物示意圖

圖 4 是運動學關系示意圖， 假設 (R)1=(a b c)T，轉盤半徑為r，轉角為φ=ωt，B的位置在動系中為(r)2=(0r0)T，出手初速度在動系中為(v)2=(vx0vy0vz0)T。

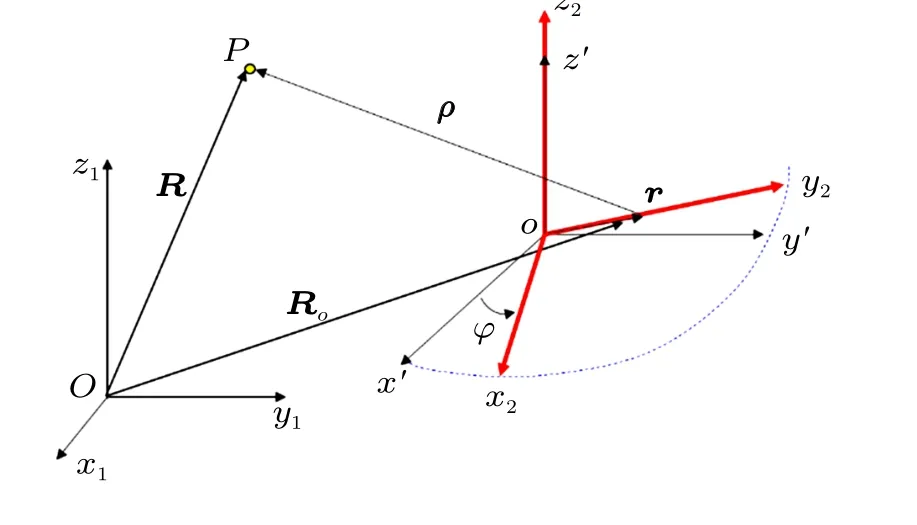
圖4 運動學關系

注意物體在不同坐標系中運動的動力學方程是不同的，根據(jù)理論力學知識，在非慣性系中動力學方程為

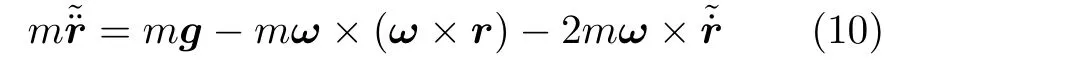
展開后的方程及初始條件為

給予具體參數(shù)

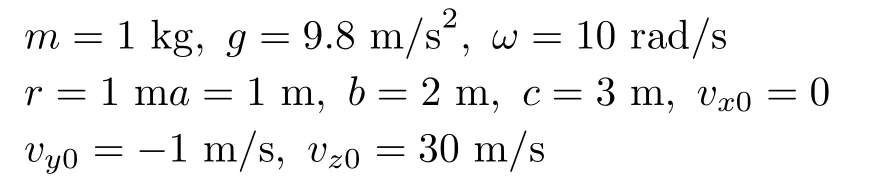
可以計算出結果，如圖5 (空間三視圖) 和圖6 (xy平面俯視圖)。

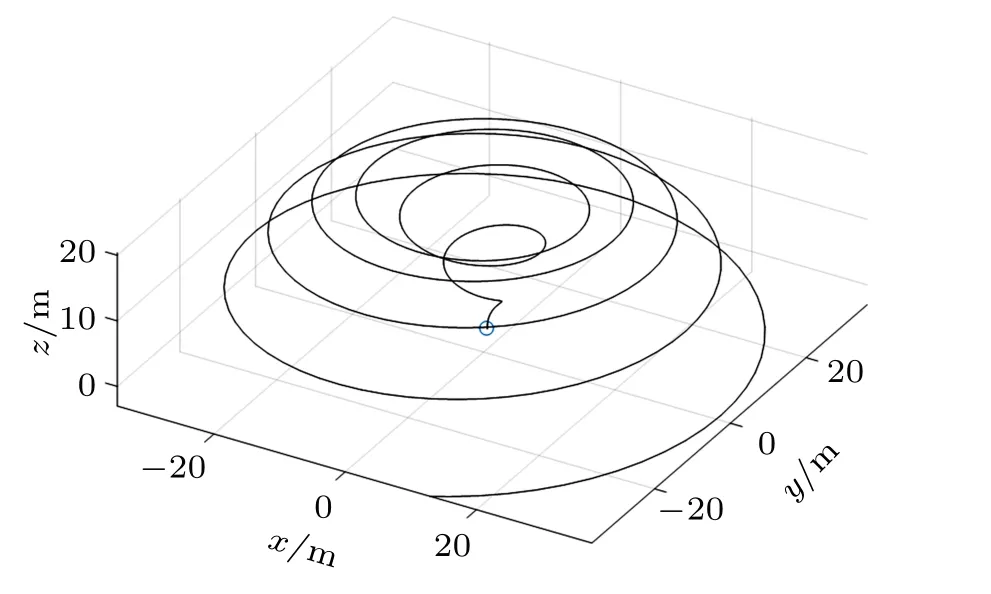
圖5 曲線的空間視圖

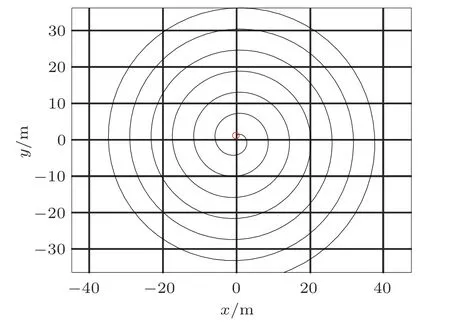
圖6 曲線的俯視圖

看起來曲線很復雜，我們怎么判斷計算結果可靠呢？

眾所周知，在慣性系中拋出一個物體其軌跡是拋物線，這是很明確的結論。因此可以這樣處理：設慣性系中算出曲線為κ1，非慣性系中算出的曲線為κ2，把慣性系中的曲線κ1數(shù)據(jù)轉換到非慣性系中得到曲線κ3，如果κ3能與κ2完全重合(兩者誤差小于給定的誤差，如積分的允許誤差)，就認為非慣性系中的結果是可靠的。

從慣性系的角度看，動力學方程有

展開后的動力學方程及初始條件為

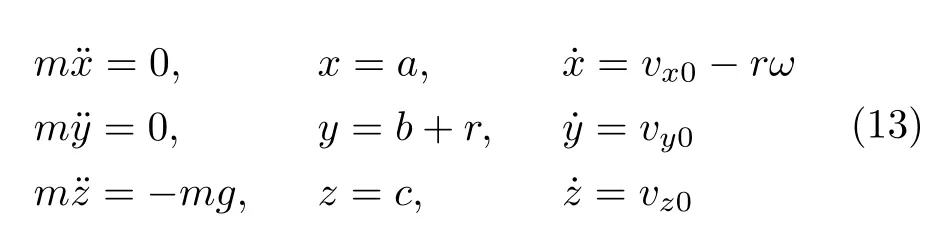
積分后結果如圖7 和圖8。我們有理由認為這些結果是合理可靠的，如曲線看起來是拋物線，俯視圖是一根直線，表示拋物線在一個平面內。當然還可以利用運動過程中的機械能守恒來判斷(略)，總之我們認為慣性系中這些曲線合理可靠。

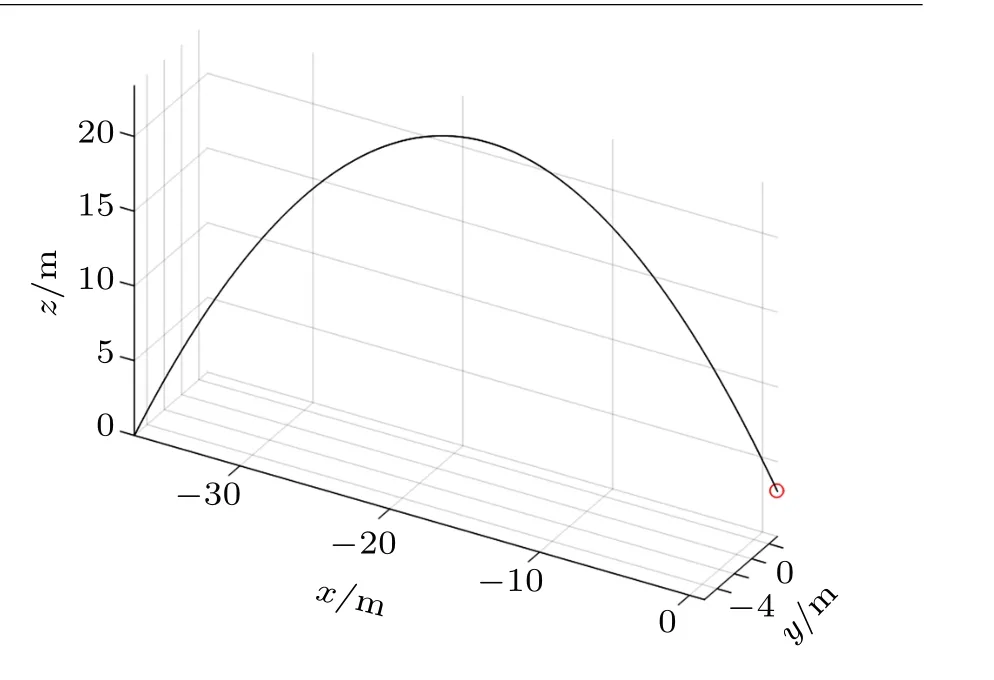
圖7 曲線的空間視圖

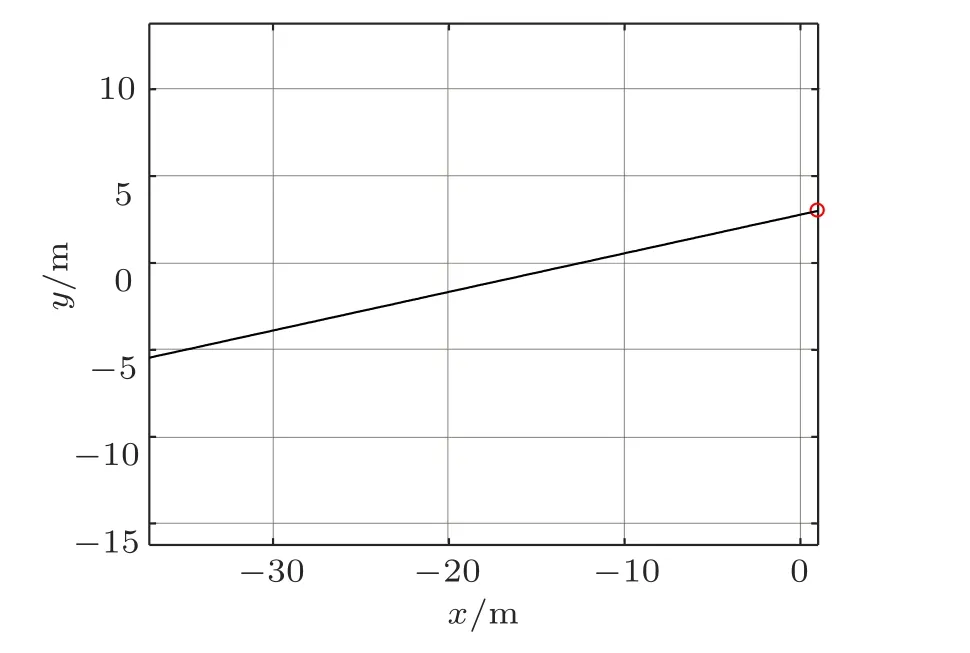
圖8 曲線的俯視圖

現(xiàn)在的問題是如何利用慣性系的結果去證明非慣性系的結果正確？

式(7) 和式(8) 給出了不同坐標系之間數(shù)據(jù)的轉換關系。具體到本問題中，轉換矩陣很簡單，z軸是平行的，退化為

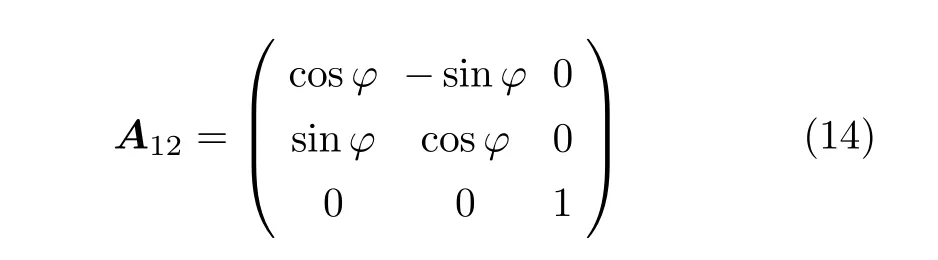
如果想把慣性系的結果轉換到非慣性系，式(7)具體為

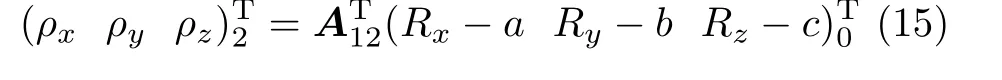
在Matlab 中，數(shù)據(jù)轉換的源代碼如圖9 所示。

圖9 數(shù)據(jù)轉換的源代碼

其中 (x1(i)y1(i)z1(i))T表示慣性系中第i個點，(x3(i)y3(i)z3(i))T是轉換后得到的非慣性系中第i個點。在Matlab 中，A12’ 表示對A12 進行轉置。

數(shù)據(jù)轉換后，可以看到每個圓圈(非慣性系中直接算出的結果)都包含一個圓點(從慣性系中轉換得到的結果)，說明兩者的精度都很高(如圖10 和圖11所示)。當然在比較的時候要注意，不同坐標系中的積分要同步，用等步長積分正好可以實現(xiàn)這一點。

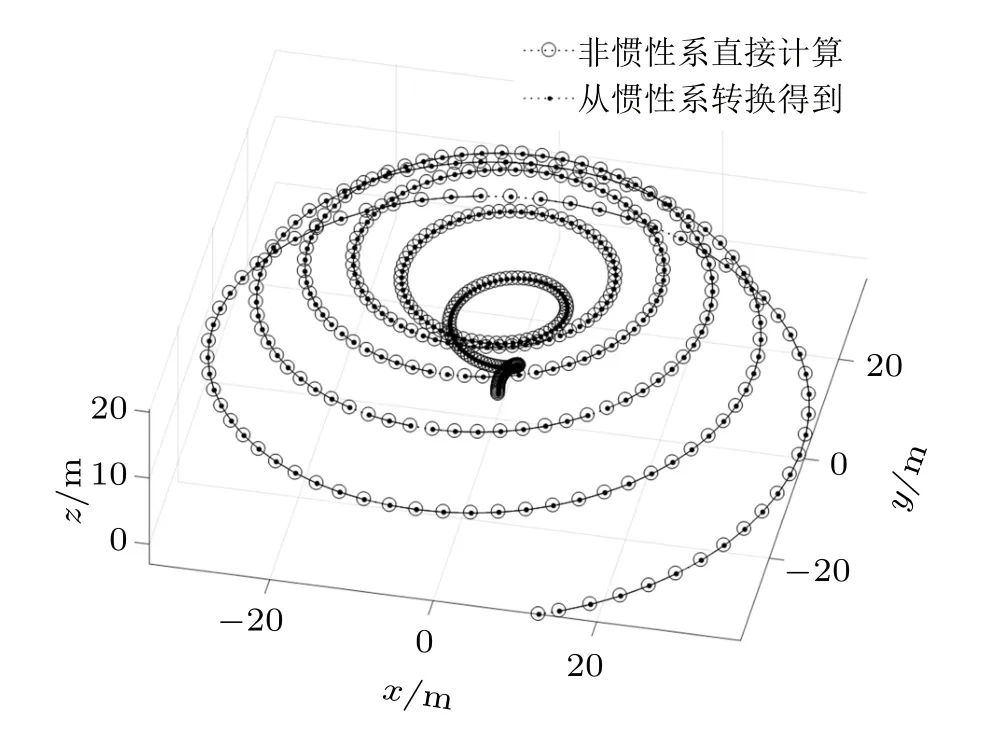
圖10 非慣性系中的空間圖

如果想把非慣性系的結果轉換到慣性系，結論依然很可靠(具體略)。綜合起來，說明圖5 和圖6的結果雖然有點出乎意料，卻是正確的。

根據(jù)這一事實，未來處理非慣性系的動力學問題時，除了直接處理非慣性系中的問題(動力學方程復雜，結果也復雜) 之外，還多了一種選擇：先在慣性系中進行分析(動力學方程簡單，結論正確性容易驗證)，然后再利用坐標系之間的轉換關系，得到非慣性系中相應的結果。

3 太陽的視運動問題

人人都知道地球繞太陽的運動很簡單，但是如果做個調查，你在當?shù)乜吹降奶栠\動軌跡(視運動軌跡) 是什么曲線？有什么特點？估計絕大部分人一時答不上來。而利用數(shù)據(jù)轉換關系可以得出既簡單又出乎意料的結論。

假設地球繞太陽為圓周運動，為簡單設365 天。在日心坐標系OXY Z中，地軸(z軸) 的單位矢量為(0，-sinθ，cosθ)T，θ=23.5°(圖12)。設時間為春分點之后第t小時，地球球心運動至

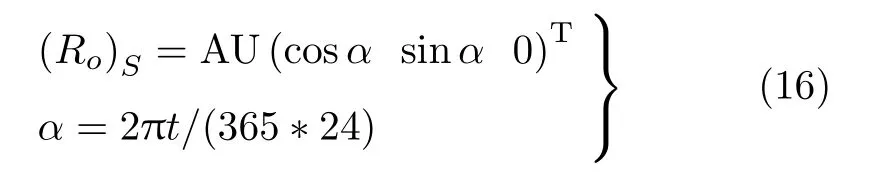
其中AU 為天文單位。設跟隨地心運動的地心坐標系為oxyz，則轉換矩陣為

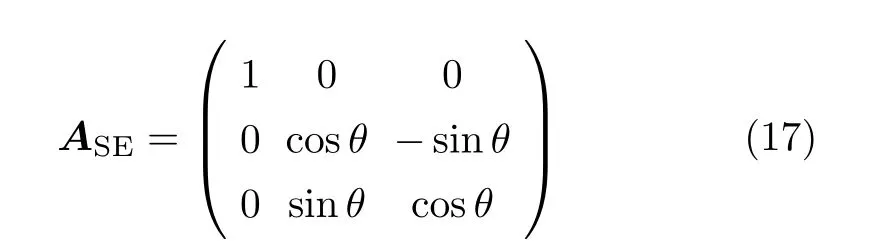
下標S 表示太陽坐標系，E 表示地球坐標系。

在地球表面P點，建立當?shù)氐臇|北天坐標系PENZ(圖12)。在地心坐標系中，P點的表達式為其中Re為地球半徑，φ為當?shù)鼐暥龋?2πt/24 為地球自轉角度。

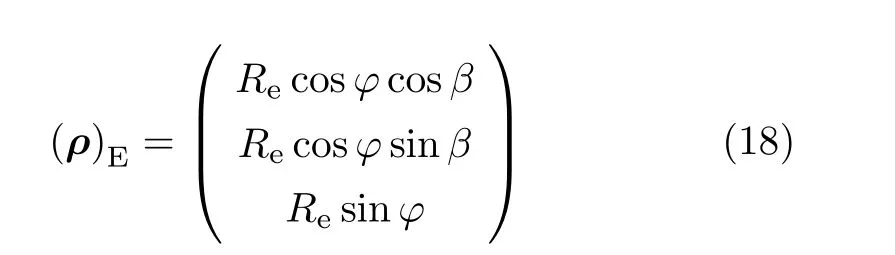
東北天坐標系相對地心坐標系的轉換矩陣為

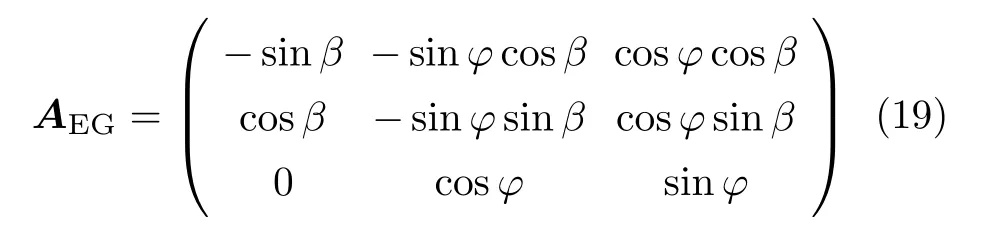
下標G 表示地理坐標系。

綜合圖12 和圖13，仍有運動學關系R=Ro+ρ，在地理坐標系中分解為

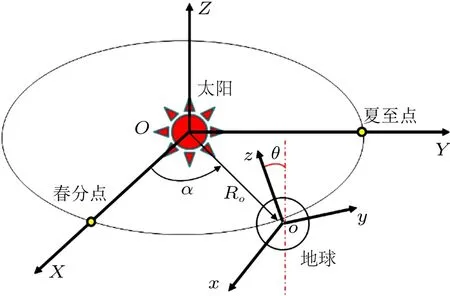
圖12 地球相對太陽的運動

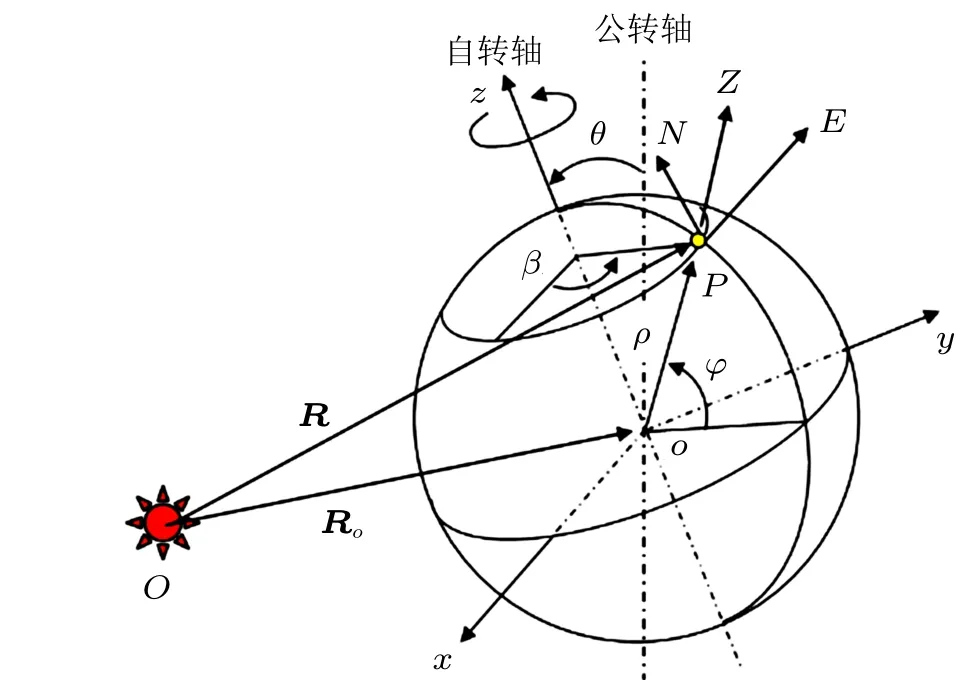
圖13 當?shù)貣|北天坐標系

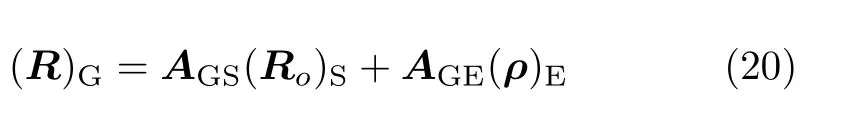
根據(jù)式(6)、式(17) 和式(19)，有

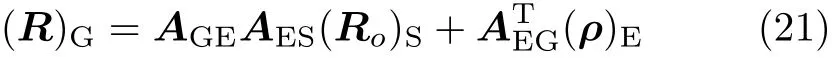
我們看到的太陽視運動， 就是式 (21) 中的-(R)G。式(21) 右邊每項都為已知函數(shù)，代入數(shù)據(jù)后太陽視運動軌跡見圖14，顯示了全年特殊日期的太陽視運動軌跡：夏至當天軌跡偏北方，冬至當天軌跡偏南方，其他時間視運動軌跡會在夏至和冬至軌跡之間緩慢地變化，春分當天軌跡居中間。我們看不到水平面下方的太陽視運動軌跡，但仍畫出。注意每一天的視運動軌跡并不封閉，因此全年的太陽視運動軌跡則很像一個彈簧，但是這個彈簧兩端半徑微小，中間半徑略大，不過差距沒有圖中彈簧那么明顯(圖15)，另外視運動軌跡很密集，在夏至與冬至之間有365 圈。

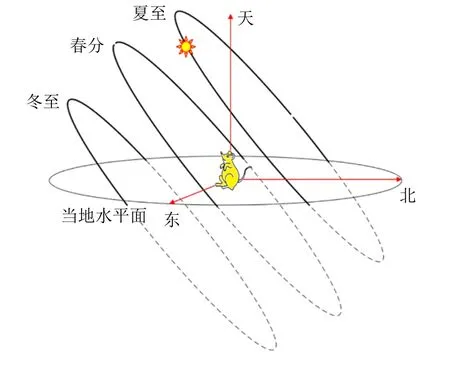
圖14 太陽某一天的視運動

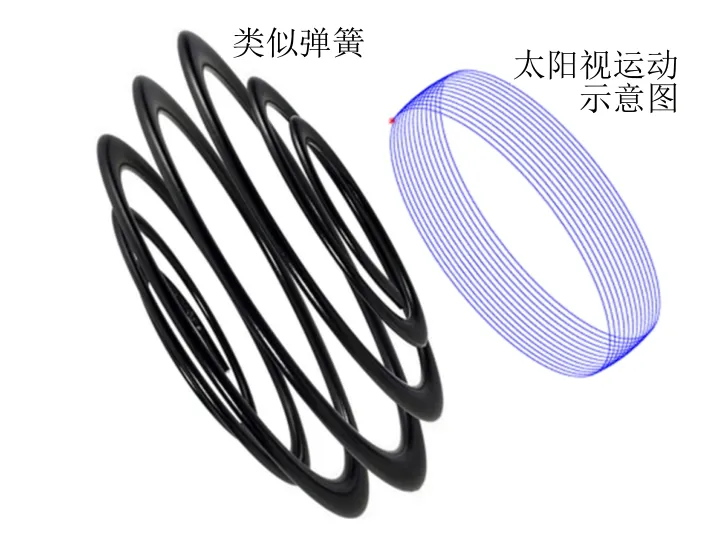
圖15 全年太陽視運動示意圖

4 小結

本文介紹了不同坐標系之間數(shù)據(jù)轉換的一般方法，利用這一方法，可以把問題先在某個坐標系中處理好，然后再轉換到另一個坐標系中。

在非慣性系拋體問題中，直接處理的方程比較復雜，結果也很復雜，難以判斷其正確性。但是在慣性系中，動力學方程很簡單，結果的物理含義也很清楚。利用不同坐標系之間的數(shù)據(jù)轉換關系，可以很容易證明兩種動力學方程的計算結果是正確的。

而在太陽視運動的問題中，從慣性系看地球的運動很簡單，但在地球上看太陽的運動，則比較復雜，出乎很多人的意料。利用數(shù)據(jù)轉換關系，可以把幾個簡單的運動(地球繞太陽的運動是圓周運動、地球上某點相對地球的運動也很簡單) 直接轉換為需要的結果。