巖石圓環試樣對徑壓縮破壞的數值模擬研究1)

辛宏舉 范寶明 張海娜 徐鑫洋 郭浩森 萬 明

*(中鐵上海工程局集團有限公司，江蘇南通 210000)

?(華東交通大學土木建筑學院，南昌 330013)

**(華東交通大學交通強省研究院，南昌 330013)

拉伸強度是誘發巖石中裂紋萌生、擴展和貫通的重要因素[1-2]，也是巖體工程結構穩定性及承載能力設計需優先考慮的重要力學參數之一[3]，因此研究巖石或類巖石材料的拉伸強度具有重要的理論及工程意義。

巴西圓盤試驗由于制樣簡單、操作方便，被廣泛應用于間接測定巖石或類巖石等脆性材料的拉伸強度[4-5]。該方法也被國際巖石力學學會[6]推薦為測定巖石或巖石類材料的間接拉伸強度最直接有效的方式。但是，圓盤試樣所受對徑壓縮載荷作用范圍較窄，加載點附近極易出現壓剪應力集中現象，誘發楔形剪切破壞[7-8]。這不但導致所測定的抗拉強度值與真實值之間存在較大的差異性，而且起裂點在應力集中附近的規律也與巴西劈裂圓盤中心起裂[7，9]理論假設相矛盾。因此，為獲得更為準確的測量結果，眾多學者提出對巴西劈裂試驗夾具[10-11]及試樣形狀[5，7-8，12]做出改進，其中圓環形試樣便是其改進的方式之一[7-9]。

歷經近半個世紀的發展，眾多學者已對圓環試樣對徑壓縮力學特性開展研究：Hobbs[7]基于彈性理論推導了圓環試樣對徑壓縮時的拉、壓應力計算表達式。Hudson[9]在分析了圓環對徑壓縮時的應力分布特征后，認為拉伸強度是試驗屬性不具備材料屬性。吳秋紅等[13]建議以拉伸變形極限值作為孔壁巖石的破裂的判斷指標。Wang 等[14]采用RFPA3D研究了不同內徑的中心孔及偏心孔的強度特征及破壞模式。Tokovyy 等[15]基于薄圓板彈性理論推導了圓環受對徑載荷條件下的應力計算表達式。Zhou等[16]采用相場法研究了圓環巴西試樣的裂紋擴展過程及峰值強度隨內徑變化的規律。上述成果均基于連續性介質力學理論及數值模擬方法研究了圓環試樣的受力變形行為及破壞特征。但是，巖石屬于典型的非均質地質材料，其損傷破壞行為更適合采用非連續性方式來描述。顆粒離散元(particle flow code，PFC) 法作為非連續性方式的一種，在細觀層面上表征巖石的損傷破壞機理具有獨特優勢，并且PFC 法在模擬圓環試樣的裂紋擴展行為方面的研究也較為鮮見。因此，本文研究可視為該方法在應用層面上的一種擴展。

本文采用二維 PFC 法中的 Flat–Joint 模型(FJM) 構建巖石圓環試樣數值模型，從細觀角度揭示圓環試樣受徑向壓縮載荷時的力學行為。研究圓環孔內徑對應力-應變曲線響應、微裂紋演化特征及破壞模式的影響。研究結果不但可驗證FJM 對模擬圓環受力變形破壞行為的有效性，同時也可加深研究者對圓環型試樣在受徑壓縮條件下的破裂機理的理解。

1 模型構建

1.1 Flat–Joint 模型(FJM)

Flat–Joint 模型首次被Potyondy[17]所提出。在相同參數的表征條件下，相較于傳統的粘結接觸模型(contact-bond model，CBM) 及平行粘結模型(parallel-bond model，PBM)，Flat–Joint 模型所模擬出的巖石宏觀破壞模式及單軸抗壓強度與拉伸強度比值更能真實地表征巖石的宏觀力學特征。因此，該模型更適合用以模擬巖石的宏細觀力學行為。在模型結構上，FJM 接觸被設想為以接觸點為中心(圖1(a)) 的局部平坦的假想平面，該平面與相鄰顆粒的假想平面處于剛性粘結狀態[18](圖1(b))。每個接觸點處的假想平面被稱為接觸面，并同時與相鄰顆粒的接觸面一起相互作用。在二維模型中，該接觸面采用一個帶有“外邊界” 結構的有限線段(圖1(b))來表示。當顆粒之間的邊界距離小于使用者設定的邊界接觸檢測距離(圖1(b) 中的g0) 時，該接觸被賦予Flat–Joint 模型參數(圖1(c))；然而，如果該接觸的相對位移大于邊界接觸檢測距離g0時，Flat–Joint 接觸模型將被移除，被移除接觸模型后的顆粒保持原有的初始運動狀態。后期顆粒在運動過程中，如果相對接觸距離再次小于g0時，該接觸將被賦予未粘結狀態的線性接觸模型(圖1(d))。

圖1 Flat–Joint 模型結構示意圖[18]

1.2 數值模型的構建

數值模型中所構建的圓環試件及加載板的幾何形狀如圖2 所示。對于二維模型而言，圓盤的厚度可視為單位厚度，在數值模擬中可忽略。圓環試件外徑R設定為50 mm，與標準巴西圓盤試樣的徑向尺寸一致，預設孔半徑r從5 mm 增加至30 mm，間隔為5 mm。為直觀方便，本文采用η來描述圓環的內徑與外徑比值，即η=r/R。η從0.1 變化至0.6，間隔為0.1。模型中全部的顆粒單元數量隨半徑比η的增加，從13 267 減少為6 745。模型采用恒定速率的剛性板加載方式。由于加載速率對模擬結果及計算效率均具有顯著性影響[19-21]，因此，在模擬開展前需要優選出合適的加載速率，以便既能保證模擬結果的穩定性又能兼顧模型的計算效率，具體優選方式詳見2.2 小節。

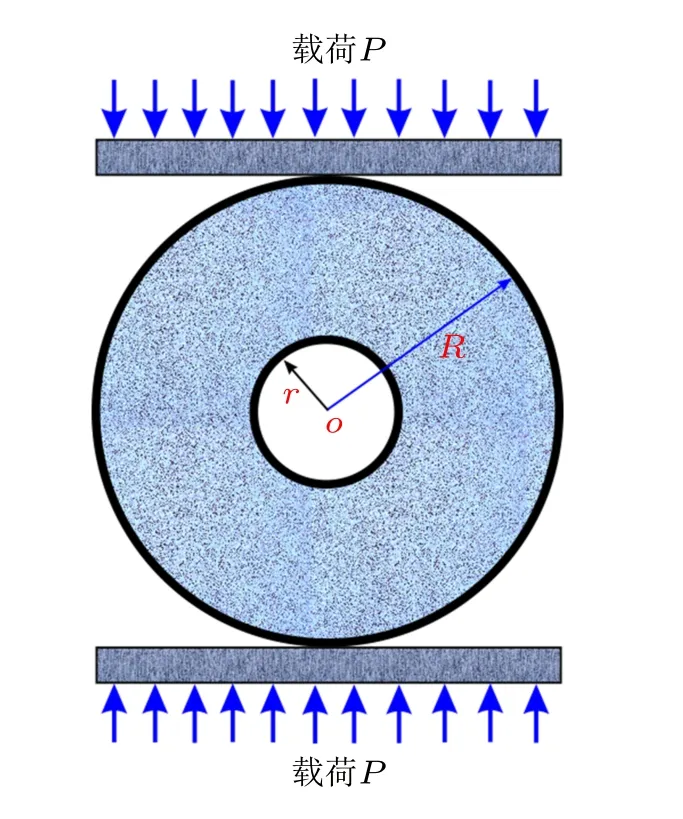
圖2 預成孔圓環試樣徑向壓縮示意圖

2 模型參數識別

模型參數識別內容應包括描述模型受力變形行為的細觀力學參數及影響模型計算效率、計算結果穩定性的配置參數。對于PFC 模型而言，配置參數主要指與力學特性無關的模型加載速率及模型精度。

2.1 細觀力學參數識別

由于巖石的細觀力學參數對數值模擬計算結果的準確性具有顯著性影響，且細觀參數無法通過室內試驗手段直接測量。因此，在采用PFC 法開展數值模擬時，必須反復微調模型的細觀參數以使其所表達的綜合宏觀力學行為能夠與巖石的宏觀力學響應特征相吻合。對于FJM 而言，所校核的細觀參數包含兩部分：(1)描述粘結顆粒的受力變形行為的細觀參數(FJM 參數)；(2) 用以表達粘結接觸破裂之后的顆粒運動性態的線性接觸參數(linear contact model，LCM 參數)。模擬巖石試樣選自文獻[13]，試樣質地結構緊密均勻，最終所校核的主要細觀參數匯總于表1 中。

表1 FJM 主要細觀參數取值匯總表

2.2 加載速率優化

加載速率是衡量模型計算效率的重要指標。此外，眾多研究結果表明[19-21]，加載速率對模擬結果的穩定性具有顯著的影響。為平衡模型計算效率及計算結果穩定性之間的競爭性，在模型加載開始前，需先優選出合適的加載速率。圖3 對比了7 種不同的加載速率條件下的應力-應變曲線響應特征。結果表明，加載速率對應力-應變曲線峰前線彈性段幾乎無影響，但是峰前小區域非線性增長段及峰后應變軟化段在較高的加載速率((2.5～5.0)×10-2m/s)條件下變化十分顯著，表現出典型的“縮放” 性特征。但是，當加載速率小于等于5.0×10-3m/s，應力-應變曲線具有高度的相似性且峰值強度也趨近于穩定。這說明在該加載速率范圍以內，模擬結果可近似認為不受加載速率的影響。綜上所述，模型所采用的加載速率為5.0×10-3m/s。

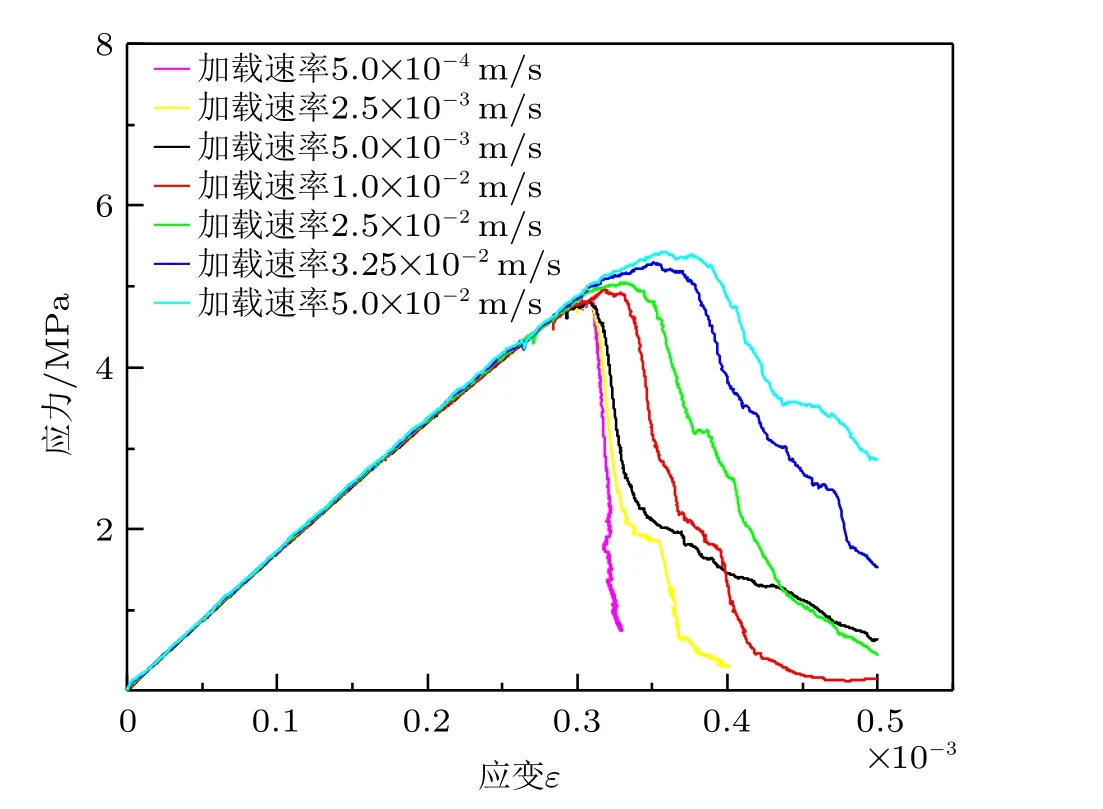
圖3 不同加載速率下的應力-應變曲線響應特征

2.3 模型精度選擇

模型精度主要是通過改變顆粒單元數量來實現，定義為數值試樣的寬度與顆粒平均直徑(2Rave，Rave為顆粒的平均半徑)的比值。模型精度對模擬結果的影響與加載速率對模擬結果的影響相類似。以峰值強度σp為例，如圖4 所示，當模型精度較低(Mr≤100)時，模擬結果不穩定，表現為峰值強度隨模型精度的增加而出現急劇衰減的趨勢；然而，當模型精度大于100 時，峰值強度雖然在局部區域內表現出小范圍的浮動(浮動幅值不超過0.3 MPa)，但整體變化卻趨于穩定。值得注意的是，雖然增加模型的精度可產生較為穩定的結果，但同時也降低了模型的計算效率。因此，綜合考量上述兩者之間的矛盾性，模型計算精度設定為100。

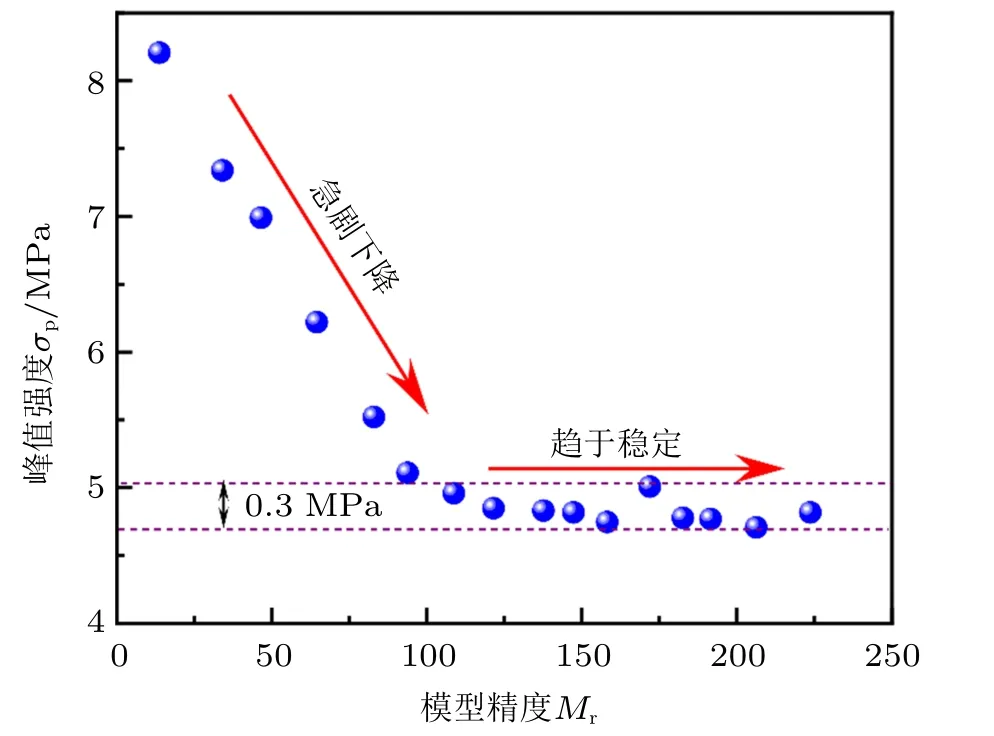
圖4 模擬的峰值強度與模型精度之間的關系

3 模擬結果分析與討論

針對不同內外徑比η的圓環試樣開展巴西劈裂試驗，分析內外徑比對應力-應變響應行為、強度特征、微裂紋演化行為及破壞模式的影響。

3.1 應變響應行為及強度特征

圖5 對比了不同內外徑比η的圓環試樣的應力-應變曲線。對于內徑較小的圓環(η≤0.2)，應力- 應變曲線與完整的巴西劈裂圓盤的應力- 應變曲線形式相類似，且在試樣破裂前存在明顯的單峰特征，然后迅速下降。隨圓環內外徑比η的增大(η≥0.4)，應力-應變曲線在圓環斷裂前具有一段平坦的區間，且峰后下降段持續時間更短。

進一步分析圖5 中的峰值強度特征(對于存在平坦區域的應力-應變曲線(η≥0.4)，峰值強度取平坦區域的平均值)，可看出：預成孔圓環對其間接拉伸強度具有弱化作用[13]。為便于分析拉伸強度的弱化規律，將圖5 中的強度值做歸一化(預成孔圓盤巴西劈裂強度與完整圓盤的巴西劈裂強度的比值)處理。圖6 分析了歸一化強度與圓環內外徑比之間的關系。結果表明，隨圓環內外徑比的增加，歸一化強度呈指數型衰減，這說明拉應力不是材料參數，而是一個結構參數，且隨圓環試樣內外徑比而變化[13]。此外，模擬的結果與文獻[13] 中所得到的擬合結果相吻合，這說明FJM 在模擬圓環試樣的變形行為及受力特征方面是有效的。

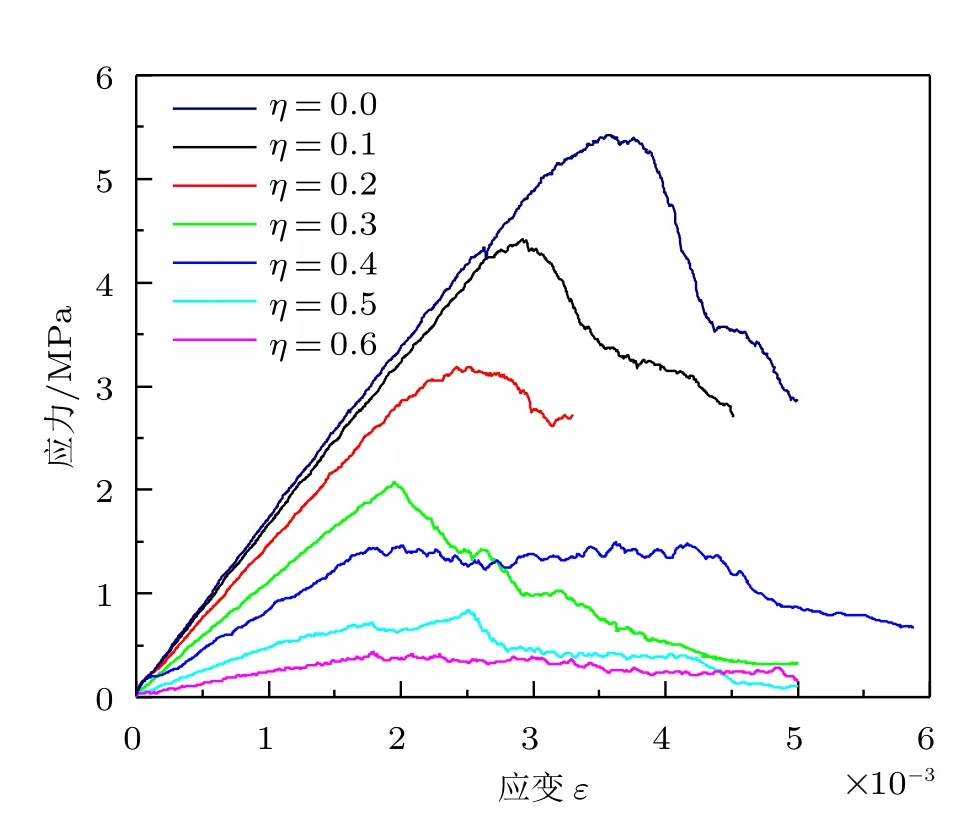
圖5 不同內外徑比η 的圓環試樣的應力-應變曲線

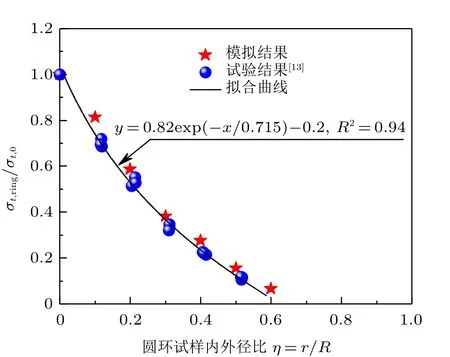
圖6 歸一化圓環拉伸強度與圓環試樣內外半徑比之間關系(其中σt，ring 為圓環試樣的間接拉伸強度，σt，0 為完整圓盤試樣的間接拉伸強度)

3.2 微裂紋演化行為

微裂紋演化行為不但影響了應力-應變曲線的變化趨勢，同樣也決定了試樣的最終破壞模式。圖7為內外徑比η為0.4 時的環形試樣徑向受壓過程的微裂紋演化全過程圖。圖中A～F六點為微裂紋全程演化過程中所選取的六個關鍵性節點，其中A和B兩點選為峰前階段，C～F四點選為峰值平坦段。圖中結果表明，在加載初期，圓環試樣在整個區域內出現若干個呈離散型分布的微裂紋。但隨加載應變ε增加至1.4×10-3時，密集微裂紋組成宏觀裂紋，從圓環內壁開始生成，并向圓環外部演化(B點)。值得注意的是，加載初期裂紋擴展方向與完整巖樣的巴西劈裂方向相一致，均與加載方向近似平行。然而，當曲線進入平坦期(C點，ε= 2.4×10-3) 后，豎直方向的微裂紋已貫通，不再進一步演化擴展。同時，與豎直方向垂直的水平向裂紋開始萌生、演化并逐步貫通(F點，ε=4.6×10-3)。從此區間可看出，水平方向的微裂紋擴展不會導致峰值強度的進一步增加。此外，通過對比C～F點的微裂紋擴展過程可知，水平向微裂紋最先由圓環試樣的外邊沿萌生并向圓環內邊緣處擴展，擴展方向與垂直的宏觀裂紋的擴展方向相反。這主要是由于垂直方向的微裂紋擴展貫通后，圓環試樣呈現出半圓環的結構特征，在兩端受壓狀態下，圓環最外側邊緣處于受拉狀態。對于內外徑比η為0.4 的圓環試樣，雖然最終的破壞模式呈現“四扇形”特征，但是全程的微裂紋演化行為具有典型的階段性特征。

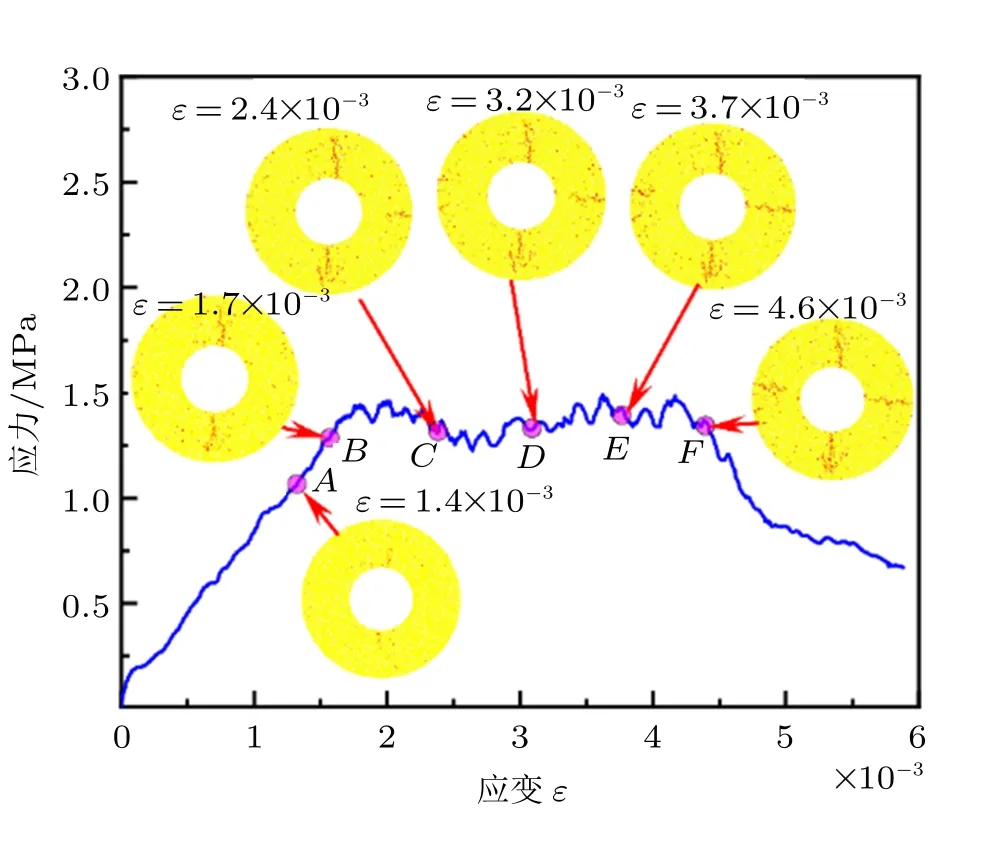
圖7 內外半徑比η =0.4 時的微裂紋演化過程圖

3.3 破壞模式

破壞模式具有微裂紋演化、貫通之后所形成的穩定的結構特征。該結構特征在一定程度上受內外半徑比的影響。圖8 對比了內外半徑比分別為0.1，0.2，0.3，0.4，0.5 時的圓環試樣在徑向受壓條件下的破壞模式數值結果與室內結果。圖中結果表明，圓環內徑對其破壞模式的影響較為顯著。當半徑比η≤0.2 時，破壞模式呈現典型的巴西劈裂特征，該特征由單條及多條復合宏觀裂紋組成。然而，當η增至0.3 時，圓盤單側出現水平向貫穿裂紋。進一步，η增至0.4 或0.5 時，宏觀破壞模式趨于穩定，表現出“四扇形”特征。對比不同內外半徑比η條件下的宏觀破壞模式演化過程可知，η= 0.3 所對應的宏觀破壞模式處于極為不穩定的狀態，極易隨著半徑比η的增加或減小向徑向劈裂或“四扇形” 模式演化。同時，模擬的結果與Li 等[22]所得到的室內試驗結果較為吻合。

圖8 內外半徑比η 分別為0.1，0.2，0.3，0.4，0.5 的破壞模式數值結果與試驗結果[22] 對比圖

4 結論

(1)加載速率及模型精度對數值試驗結果的穩定性具有重要影響。為獲得穩定的模擬結果，建議模型所設定的加載速率不宜超過5.0×10-3m/s，所設定的模型精度值不低于100。

(2) 內外徑比η對應力-應變曲線行為的影響較為顯著：對η≤0.2 的圓環試樣，應力-應變曲線特征與完整巴西劈裂圓盤的曲線變化行為相類似，存在明顯的單峰特征；隨η的增大，應力-應變曲線存在一段由水平向裂紋擴展而誘發的平坦區間。

(3)內外徑比對圓環試樣的峰值強度具有弱化作用，且這種弱化規律可采用指數函數來表達。

(4)隨內外徑比η的增加，圓環試樣的破壞模式由徑向劈裂向“四扇形” 破壞模式演化，且η= 0.3為圓環試樣破壞模式演化的關鍵值。