氦原子能級的變分微擾計算

白占武，閻占元

(華北電力大學 數理系，河北 保定 071003)

氦原子能級結構是多電子原子能級結構的基礎, 因而一直是人們感興趣的研究對象.計算主要采用變分法和微擾法.變分法求解的關鍵是選取合適的試探波函數.因此大量研究通過設計試探波函數并增加變分參數的個數來提高計算精度.例如,文獻[1]結合物理圖像提出二參數變分法并計算出類氦原子的基態能量.計算得到的基態能量與實驗值的相對誤差為0.95 %.文獻[2]基于Hylleraas 變分波函數得到氦原子的基態能量.利用 Mathematica 軟件的符號計算功能求積分和解行列式方程,采用11項展開的Hylleraas波函數進行計算,得到的基態能量的理論值和實驗數據誤差小于0.04 ‰.文獻[3]通過顯式考慮電子間關聯效應,用變分法計算了氦原子和類氦離子的基態能量,氦原子基態能量的理論值和實驗數據誤差為0.42 %.文獻[4]用九個類氫原子波函數組合成試探波函數,用變分法近似計算了氮原子基態及第一激發態的能級;1S2S兩個能級與實驗數據誤差分別為2.4 %和4.8 %.文獻[5]基于拉卡方法,用兩參數變分法計算了氦原子低激發態(電子組態為 1s2s, 1s2p 等)的能量;1S2S兩個能級與實驗數據的誤差分別為0.52 %和1.04 %.

與變分法不同,微擾法求解的關鍵是微擾項要足夠小.在處理類氦原子問題時,通常將電子間的相互作用能看作微擾項,但是實際上該相互作用能并非很小.在實際應用中,變分法用得比微擾法廣泛得多，主要是因為微擾法計算上的困難.在進行能量的二級或更高級的微擾修正的計算中,必須計算遍及無窮個不連續態的求和以及遍及所有連續態的積分, 而這些計算是非常困難甚至是不可能的.但是,微擾法規范的計算可以系統地改進計算結果.文獻[6]用微擾法計算的基態能量與實驗數據誤差為5.3 %.文獻[7]將變分法與微擾法相結合,利用低級微擾的能量和波函數,用變分方法得到了下一級微擾的能量和波函數.

本文將變分法與微擾法相結合.首先用變分法計算氦原子第一激發態1S2S的兩個能級,再進行微擾計算.由于變分法是用帶參數的可解哈密頓量本征函數去逼近原哈密頓量的本征函數,再將剩余哈密頓量的矩陣元看做微擾將是一個好的近似.我們給出了微擾矩陣元的解析表達式,輔助以matlab數值計算,得到了二級微擾近似下的能量.

1 變分法計算

考慮到氦原子中另外一個電子的屏蔽作用，將核電荷數λ作為一個變分參數.哈密頓量的可解部分取為(原子單位)

(1)

總哈密頓量：

(2)

其中

(3)

考慮到1S2S態自旋波函數有對稱(正氦)、反對稱(仲氦)兩種形式,相應的空間波函數有反對稱、對稱兩種形式.

(4)

(5)

λ1=1.8497，λ2=1.8145

及

(6)

上述變分法的結果已包含了能量的一級微擾修正.

2 變分微擾計算

下面計算能量的二級微擾修正.將徑向波函數寫成如下形式

(7)

其中

ξ1=2λr1/m,ξ2=2λr2/n

C(ml,i)是合流超幾何函數F(-m,2l+2,ξ1)的展開系數【8】,C(nl,j)類似.這樣

R10(r1)=N10e-mξ1/2,

(8)

對于未對稱化的波函數,微擾矩陣元的解析表達式為

(9)

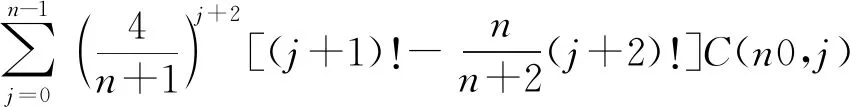
(10)

(11)

其中dk(a,k)=a(a-1)...(a-k).

考慮波函數的對稱性,當m≠n時,有

(12)

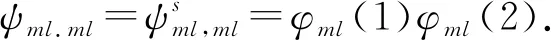
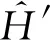
(13)

(14)

當m=n時,

(15)

能量的二級微擾修正為

(16)

(17)

3 總結