非線性振動中周期與振幅和能量關系的級數表達式

郝繼光，黃亦斌

(1. 南昌市灣里區第一中學，江西 南昌 330004；2. 江西師范大學 物理與通信電子學院，江西 南昌 330022)

通常對振動的處理方式，是將勢能函數在極小值點處取到二次項，從而求出振動的頻率和周期. 這等價于把該振動視為簡諧振動處理. 若想考慮振動頻率與振幅的可能關系，在這一階是不可能得到的，需考慮高階效應，成為非線性振動問題. 這一關系一直是大家比較感興趣的問題[1-7]，其中針對單擺的研究較多[4-7]. 這一關系一般難以存在有限表達式，故而我們可以就一般情形尋找其級數表達式. 由于計算量較大，我們使用了Mathematica 軟件，其中除常見簡單命令外，我們還大量使用了Series(冪級數展開)、DSolve(解微分方程)，Collect(合并同類項)等命令.

設振子的勢能在極小值點(取為x=0，且V(0)=0)附近的泰勒級數為

(1)

上式ω>0.

由能量守恒，有

(2)

將其對時間求導，得

(3)

設正向最遠到達x=A處，取此時為初始時刻.茲使用微擾法求其級數解(在數學上類似的例子見參考文獻[8])，即設其解為

x=x0+x1+x2+x3+x4+…

(4)

1 精確到二階的結論

把式(4)代入方程(3)，精確到二階解x2，得方程組：

(5)

于是，使用DSolve命令，精確到二階的解為

(6)

注意其中有非周期項，而我們的振動顯然是周期性的.其原因就在于2π/ω并非真正的周期.可令

ω=Ω+aA+bA2+…

(7)

即Ω為真正的圓頻率，其初級近似為ω，高階部分則表示為A的級數.僅將上式代入式(6)中的三角函數中(其他位置的ω不做替換，因為我們要盡量用原始的系數ω2、k1、k2、…來表示)，并利用Series命令展開到A3項，令每一階的新非周期項的系數為0，即可確定式(7)中的系數a、b.這樣得到的T=2π/Ω才是真正的周期.由此可以確定ω、Ω的關系：

(8)

同時式(6)變為

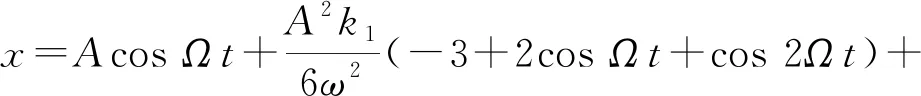
(9)

它恰為式(6)去掉非周期項、并將所有三角函數內的ω換為Ω的結果.另外，由式(9)可以看到，平均位置(坐標的時間平均值，即常數項)為

(10)

設反向振幅為B，即反向最遠到達-B處.由于初始條件x=A和x=-B不可區分(或平權)，故以上各式若做替換A→-B，則應該保持不變(其中式(6)和式(9)還需重新定義時間零點).這可稱為“雙向振幅交換不變性”.式(10)的交換不變性給出

(11)

由此得到A和B的相互關系為

(12)

由于式(11)只有兩項，所以式(12)也只能保留兩項.

2 精確到四階的結論

考慮四階效應時，把式(4)代入方程(3)，得到的兩個新方程為

(13)

(14)

解x3,x4分別對應A4,A5項，利用DSolve命令可得到結果，但比較冗長，從略.它們中當然也存在非周期項，如x3中的這些項：ωtsinωt,ωtsin 2ωt.為消去各階非周期項而需做的變換(與式(8)對應)是

(15)

而x3,x4用Ω可表示為

(16)

56064ω4k1k3-5760ω6k4)cosΩt+

1584ω4k1k3+1080ω6k4)cos 5Ωt]

(17)

式(9)、(16)、(17)之和就是方程(3)精確到4階的解. 容易得到，平均位置為

(18)

由式(15)，周期T=2π/Ω為

(19)

此外，由式(2)，能量與振幅A的關系為

(20)

以上各式應該都具有“振幅交換不變性”. 具體地，由于E(A)=E(-B)，上式可以給出雙向振幅B與A的關系為

(21)

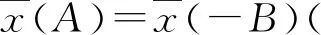
利用InverseSeries 命令反解式(20)，得到振幅A與能量的關系：

(22)

其中，能量含在A0中，

(23)

反向振幅B與能量的關系很容易由式(22)得到，只要作替換A→-B,A0→-A0即可，或作替換A→B且把k1,k3,k5、…添負號亦可.把式(22)代入式(19)，即可得到周期與能量的關系：

(24)

至于平均位置與能量的關系，可利用式(18)和(22)，得到

(25)

3 例證

例1：單擺

單擺的勢能為V(θ)=mgL(1-cosθ).記x=Lθ，將勢能展開到x6項，與式(1)對比，得

由前面所說的一般程序，或由式(9)、(16)、(17)，得到解為

(26)

其中θ0=A/L為角度θ的振幅.而

(27)

故有

(28)

該結果與其用橢圓積分表示的精確結果展開式的前5階相同，也與單擺周期的另一級數表達式

(29)

例2：平方反比引力場中的近圓軌道

平方反比引力場中粒子的徑向方程為[8]

(30)

其中m1為粒子質量，m2為中心天體質量，常數E和h分別是粒子的總能量和單位質量的角動量，而V(r)為徑向運動的等效勢能.V(r)存在極小值點r0=h2/Gm2，極小值為-(Gm2)2m1/2h2.r=r0即圓軌道.對于近圓軌道，令r=r0+x，將V(r)展開到x6項，并與式(1)對比，得

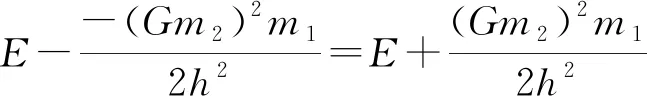
(31)

其中e就是偏心率.于是，式(24)給出周期與能量的關系為

(32)

其中能量含在e中，且用到了r0的定義.式(25)給出平均半徑與能量的關系為

(33)

該結果式(32)、(33)是否正確？可以用嚴格結果檢驗.平方反比引力場中存在如下關系[9]：

(34)

其中a為半長軸.前者就是開普勒第三定律，后者是用軌道參數表達的能量.兩式消去a，將其中的E用e表示，并利用ω的定義，可得

(35)

其級數展開正是式(32).另一方面，對平方反比引力場中的粒子，有[9]

(36)

前者是軌道方程，后者表示角動量守恒. 由兩式可計算半徑的時間平均值為

將上面的周期表達式(35)代入，并利用ω,r0的定義，得到平均半徑為

(37)

其級數展開正與式(33)相符.