孤島微電網頻率μ-H∞魯棒控制

吳麗珍，丁安邦，陳偉,3，郝曉弘,3

(1.蘭州理工大學 電氣工程與信息工程學院，蘭州 730050； 2.甘肅省工業過程先進控制重點實驗室，蘭州 730050；3.蘭州理工大學 國家級電氣與控制工程實驗教學中心，蘭州 730050)

0 引 言

微電網(microgrid,MG)是將各種分布式電源(distributed generation,DG)、負荷、儲能單元以及控制設備結合起來的可控獨立系統，既可以與大電網并網運行，也可以孤島運行，是分布式電源接入配電網的橋梁與紐帶[1-3]。微電網由于自身容量小、慣性弱、出力不確定性強、頻率調節能力和阻尼特性差等原因，使頻率穩定問題日益凸顯[4]。對于微電網頻率穩定控制問題，國內外已開展許多相關研究。微電網主要有主從控制、對等控制和分層控制等三種控制方式[5]。傳統下垂對等控制方式受線路阻抗影響難以實現有功和無功功率的精確分配，導致穩定狀態下微電網頻率偏離額定值。分層控制方法已成為微電網穩定控制的主要形式，頻率二次控制得到深入研究。文獻[6]提出了一種基于變步長自適應的分散協調控制方法，實現了直流母線電壓和頻率的零誤差調節。但該方法未考慮多模式間切換及環流對分配精度的影響問題，并且控制器設計較為復雜。在文獻[7]中，采用Hopfield模糊神經網絡方法和粒子群優化(particle swarm optimization,PSO)與模糊邏輯相結合的方法來調節頻率偏差，但該方法具有模糊性不能保證所設計控制器的控制精度。

微電網運行方式的改變，將導致網絡等值參數和運行參數的變化，將引起微電網內控制對象參數攝動的問題，給系統頻率控制帶來困難。文獻[8]通過考慮多目標約束問題，得到PID控制器優化參數，但無法解決對于系統中參數攝動的問題。魯棒控制是一種實用性較強的現代控制方法，其中H∞控制理論是目前解決魯棒控制問題中較優越的理論體系，已應用到了變流器的線性控制器中。文獻[9]提出了一種分散魯棒控制策略，為每個發電單元設計了魯棒控制器。文獻[10]設計出負荷頻率H∞魯棒控制器，并利用線性矩陣不等式方法來求解魯棒控制器。在文獻[11]中，為了提高在不確定性情況下的頻率控制魯棒性能，提出了基于混合H∞/H2和PSO的混合H∞/H2參數整定方法。文獻[12]設計了一種H2/H∞控制器對柴油發電機進行有功功率調節，對風能和負荷的變化而引起的功率偏差進行補償，達到了微電網頻率控制的目的。文獻[13]針對交直流混合微網提出了一種基于H∞混合靈敏度的交直流混合微網頻率控制方法，解決了頻率波動及控制對象參數攝動的問題。在文獻[14]中針對孤島微電網頻率穩定性問題提出了一種基于μ綜合的魯棒控制器設計方法，但沒有討論不確定性建模對控制性能的影響。

上述文獻的建模過程中，均沒有考慮網絡延時對微電網系統性能的影響。然而，網絡化的微電網系統二次控制中，網絡延時不可避免，將降低系統魯棒性，甚至導致系統不穩定[15]。為此，文獻[16]針對多區域互聯微電網中的時滯負荷頻率控制問題，設計了基于線性矩陣不等式方法的輸出反饋魯棒控制器。文獻[17]則采用馬爾可夫過程估計延時和數據包丟失，提出了基于粒子群優化算法的PI控制器，來保證負載頻率穩定。但均未考慮系統結構不確定性問題。

本文在考慮微電網頻率二次控制中網絡通信延時、系統參數攝動以及結構不確定性的基礎上，提出了一種基于μ-H∞綜合的微電網系統頻率控制方法。首先，將參數攝動與閉環控制通信延時作為非結構不確定性擾動整合到H∞控制中。其次，在設計的H∞控制器基礎上考慮結構不確定性問題，結合D-K迭代法設計出μ-H∞控制器。最后，通過Matlab/Simulink仿真與dSPACE1007半實物仿真平臺實驗，驗證了所提μ-H∞控制方法在參數攝動、通信延時和結構不確定的情況下系統有較好的魯棒性能。

1 微電網系統動態建模

1.1 孤島微電網結構

本文研究的孤島交流微電網由風力系統(wind power,WP)、光伏系統(photovoltaic，PV)、柴油發電機(diesel engine generator,DEG)、微型渦輪(micro-turbine,MT)、燃料電池(fuel cell,FC)以及儲能(battery energy storage,BES)、交流負載等組成，如圖1所示。

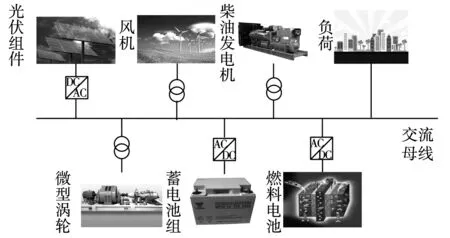
圖1 孤島微電網結構Fig.1 Structure of isolated microgrid

有功功率的供需不平衡是導致微電網頻率波動的主要原因，可通過平衡有功功率來減小頻率的偏移。當孤島交流微電網中風力、光伏發電輸出功率不確定以及負荷的隨機波動，導致系統功率不平衡，即式(1)左右不相等時，通過頻率二次控制器對柴油發電機組、微型渦輪和燃料電池進行協調控制，進而控制微電網的功率平衡。

PLoad=PDEG+PMT+PFC+PWP+PPV±PBES。

(1)

式中：PLoad、PDEG、PMT、PFC、PWP、PPV、PBES分別為用戶負荷、柴油發電機功率、微型燃氣輪機功率、燃料電池功率、風力發電系統輸出功率、光伏發電系統輸出功率、儲能輸入/輸出功率，其上下限表達式分別為

(2)

式中，左邊變量為下限值，右邊變量為上限值。

圖2是微電網系統頻率控制動態響應模型原理框圖，其中：ΔPWP和ΔPPV分別是風力和光伏功率的變化量；D為阻尼系數；M是微電網頻率響應的慣性系數，為不確定參數，作為輸出乘性攝動施加于系統G(s)，其模型參數如表1所示，其中Pini為初始功率，Pmax為最大功率，Pmin為最小功率，Pbase為微電網容量。

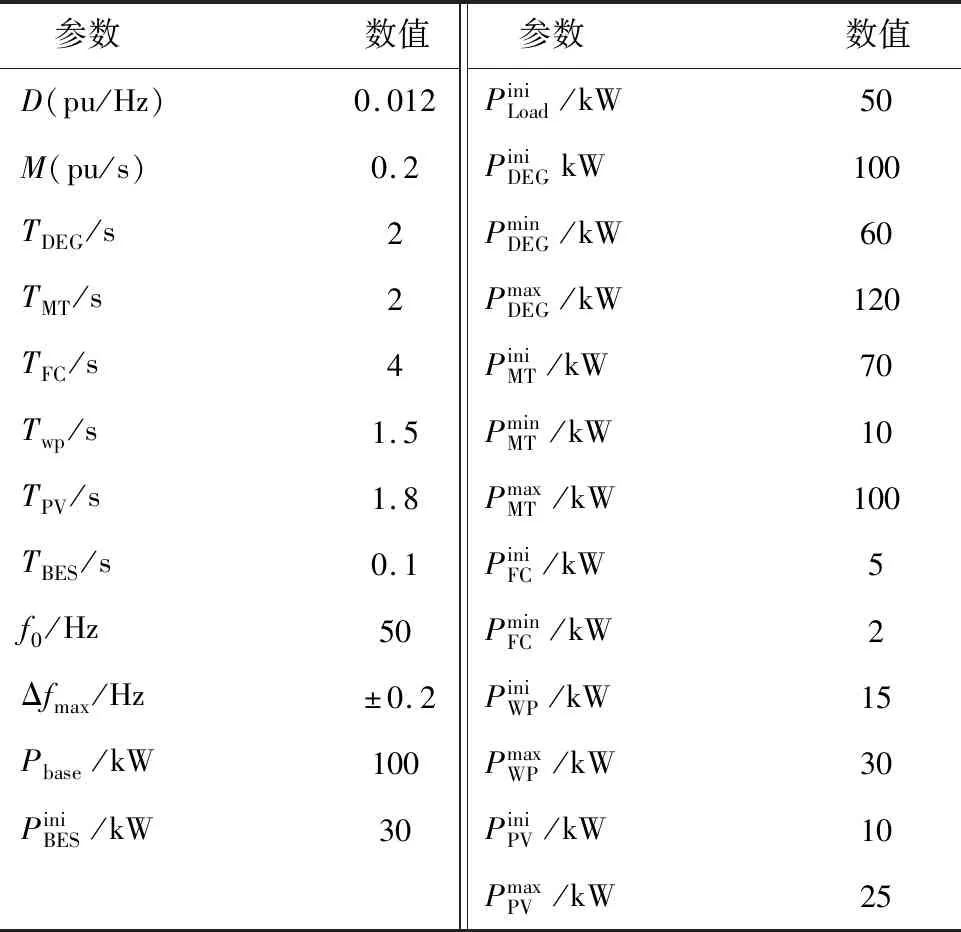
表1 模型參數Table 1 Model parameter

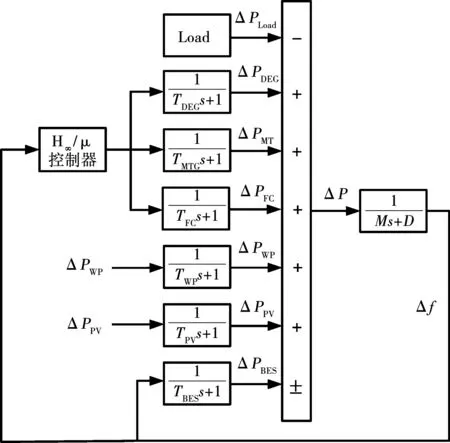
圖2 微電網頻率控制原理框圖Fig.2 Block diagram of MG frequency control

實際用戶負荷、風力發電系統、光伏發電系統功率預測會存在偏差，其中負荷偏差、風力發電輸出功率偏差、光伏發電功率偏差[18]可表示為

(3)

功率偏差ΔP與頻率偏差Δf的關系為

Δf=[1/(Ms+D)]ΔP。

(4)

1.2 微電網系統動態模型

微電網魯棒控制中一種有效的模型表示方法是線性狀態空間方程[19]。考慮通信延時的微電網狀態空間模型為

(5)

(6)

(7)

當系統發生突變時，控制器迅速給出控制信號，控制微型渦輪，柴油發電機和燃料電池改變有功出力，維持微電網電壓頻率穩定。

2 微電網頻率μ-H∞控制器設計

2.1 H∞與μ綜合設計方法

H∞魯棒控制標準框圖如圖3(a)所示，其中，w為外部輸入信號(包括參考輸入、擾動、噪聲等),u為控制器輸出信號；y為觀測信號；z為性能輸出信號；K(s)為控制器,G(s)代表廣義被控對象。其中G(s)由式(8)表示，其傳遞函數Twz(s)表達為式(9)。

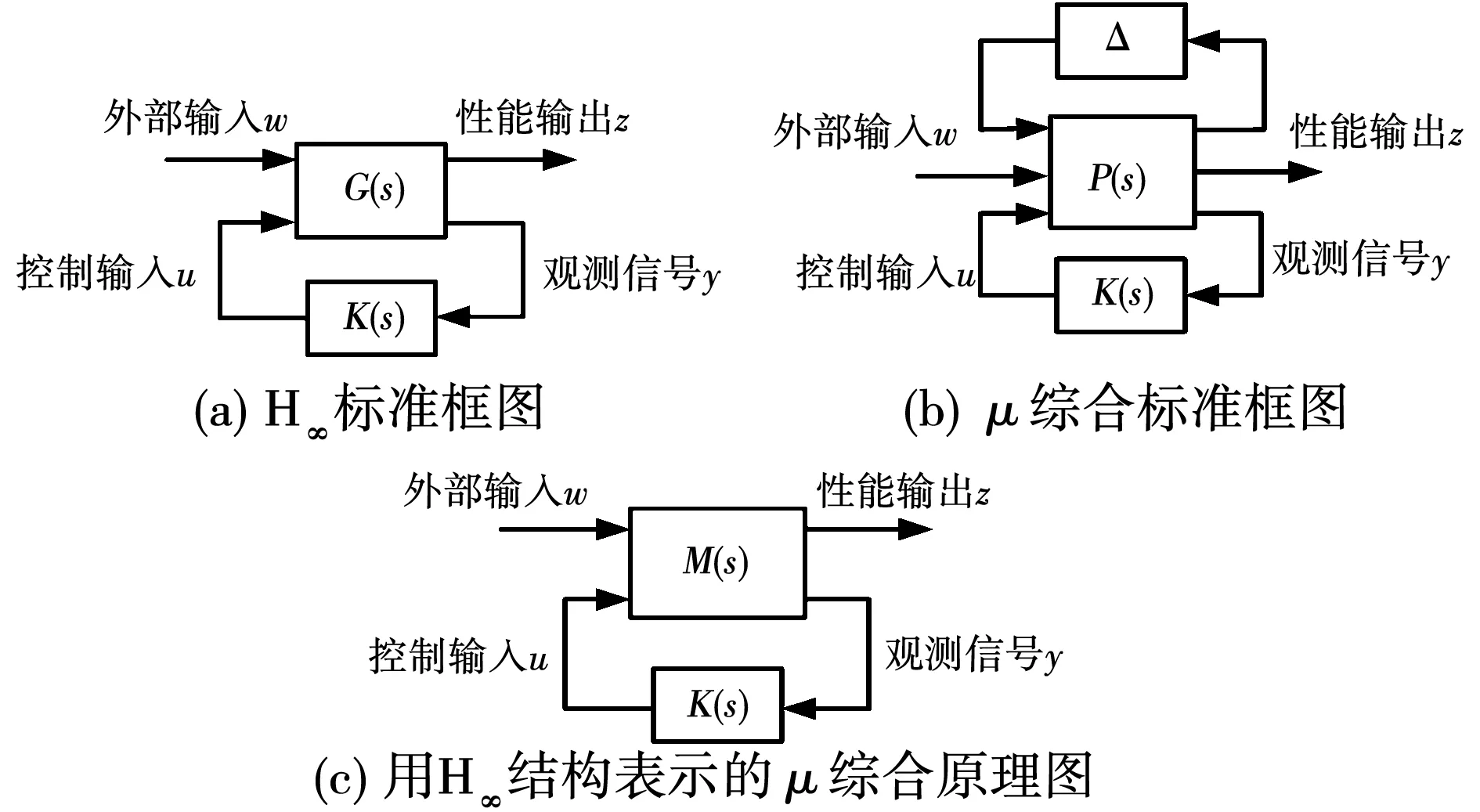
圖3 控制標準框圖Fig.3 Control standard configuration

(8)

Twz(s)=G11(s)+G12(s)K(s)(I-G22(s)K(s))-1G21(s)。

(9)

H∞控制問題實質上是求解一個控制K(s)，使得在系統穩定的前提下滿足‖Twz(s)‖∞≤1[20]。

圖3(b)為μ綜合標準框圖。其中：P(s)為廣義被控對象；K(s)為控制器；Δ為擾動塊。圖3(c)中，廣義被控對象M(s)是由P(s)和K(s)共同組成的閉環系統。M(s)=Fu(P,Δ)，由此將μ綜合問題經轉化為了H∞控制器設計問題。M(s)中包含不確定擾動模塊Δ。Δ可用式(10)來表示。

Δ={diag[δ1Ir1,…,δkIrk,…,Δf],δi∈C,Δj∈Cki×kj}。

(10)

μ函數定義為

(11)

式中，σ為矩陣Δ的最大奇異值。穩定控制器K(s)應使得式(12)最小從而達到魯棒性能。

(12)

式中，ω為系統角頻率。

在求出的H∞控制器K(s)的基礎上，結合μ綜合中的D-K迭代法，使‖Twz(s)‖∞=‖Fl(M(s),K(s))‖∞值達到最小，即可設計出μ-H∞控制器。

2.2 控制器設計

H∞魯棒控制中動態參數攝動的不確定性為“非結構不確定性”[21]。混合靈敏度控制是魯棒控制器的設計方法之一。在設計過程中，同時考慮了外部擾動和內部參數攝動，能夠滿足系統的魯棒性能[22]。為此，首先將狀態空間方程式(5)中的通信延時轉化為系統的一個不確定塊Δ(τ)，然后采用乘性攝動進行不確定性建模，進而采用混合靈敏度控制方法設計出魯棒控制器。

所設計的H∞魯棒控制結構框圖如圖4所示。

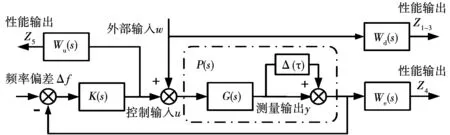
圖4 H∞魯棒控制結構框圖Fig.4 Structure diagram of H∞ robust control

圖4中：w，u，z{1-5}，y分別是外部干擾輸入，控制信號，期望性能信號和測量輸出；We(s)、Wu(s)和Wd(s)為加權函數。若將閉環系統通信延時作為外部擾動集中到攝動模塊Δ(τ)中，則考慮不確定性的系統P(s)=(I+Δ(τ))G(s)。

H∞魯棒控制的目標是使系統輸出對外部擾動和通信延時均不敏感，且當參數攝動時系統仍然保持穩定。在此，將系統靈敏度函數和互補靈敏度函數定義為

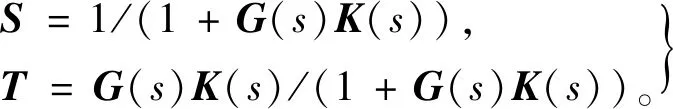
(13)

標準H∞控制問題是求解一個控制器K(s)，使得在系統穩定的前提下滿足式(14)。

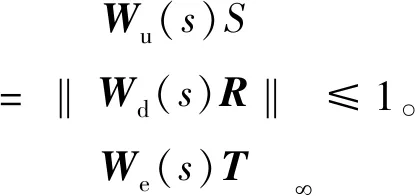
(14)

由式(14)轉化得

(15)

由式(15)可以看出，選擇適當的加權函數We(s)、Wu(s)和Wd(s)可以改善系統的魯棒穩定性和魯棒性能，從而達到設計要求[23]。式(16)～式(18)為選定的加權函數。

(16)

Wd(s)=0.01I3×3，

(17)

(18)

μ-H∞控制器在考慮通信延時問題的同時，包含了不確定性系統P(s)的擾動不確定性，更好地滿足了魯棒性能要求，在H∞魯棒控制基礎上進一步提高了控制器的魯棒性能[24]。

根據狀態空間方程式(5)，結合所設計的H∞控制器，可以得到μ-H∞控制結構框圖如圖5所示。

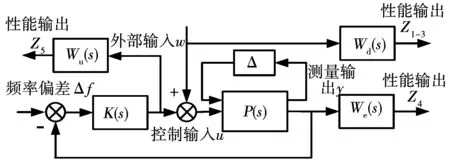
圖5 μ-H∞控制結構框圖Fig.5 Structure diagram of μ-H∞ control

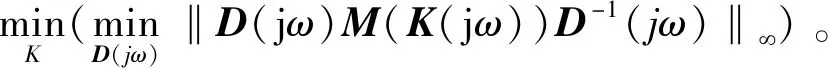
D-K迭代法的思想是輪流令D或K最小化，同時使另一個保持不變。用D-K迭代法設計μ-H∞控制器的步驟為：

步驟1:確定D(s)，根據min‖D(s)M(K)D-1(s)‖∞可以得到一個H∞控制器K(s)。

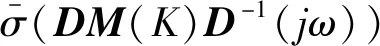
步驟3:將每個D(jω)帶入后再重復迭代，直至‖D(s)M(K)D-1(s)‖∞<1或者無窮范數不再減小，則迭代結束。

3 仿真與實驗結果分析

3.1 系統結構不確定情況下穩定性分析

本文考慮不確定參數M為具有±50%偏移，通過Matlab軟件仿真分析50%M，100%M和150%M三種情況下系統動態響應能力，系統階躍響應如圖6所示。

從圖6可以看出，系統調節時間短，超調量小，具有較強的動態響應能力，階躍響應曲線都不發散，系統穩定。

圖6 存在不確定性時的系統階躍響應Fig.6 Step response of systems with uncertainties

系統頻率響應特性如圖7所示，表2是系統性能指標。從圖7與表2可以看出在M存在±50%偏移的情況下，系統幅值裕度大于-40 dB，相角裕度大于50°，調節時間小，截止頻率大。采用所設計的控制器，系統響應速度快，有較好的魯棒性。

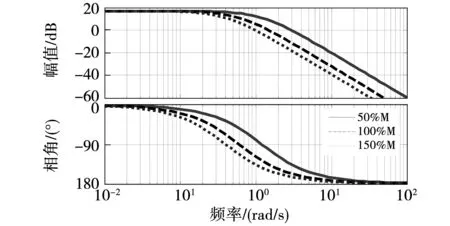
圖7 存在不確定性時的系統波特圖Fig.7 System Bode diagram with uncertainty

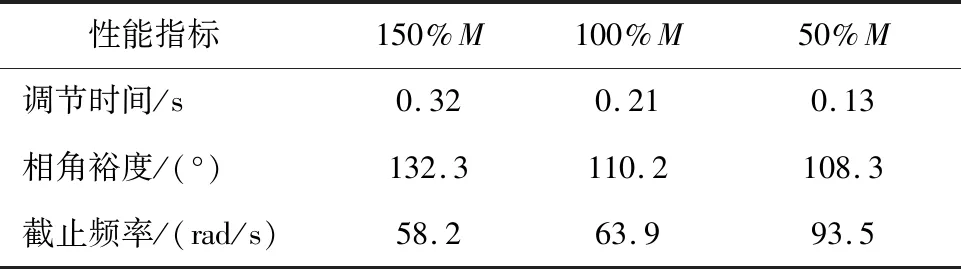
表2 性能指標Table 2 Statistic of performance indicators

3.2 具有延時情況下系統穩定性分析

在建立的H∞魯棒控制器系統中，假設時間延遲分別為：τ=0.5 s，τ=0.8 s，τ=1.2 s，τ=1.5 s，相應的仿真結果如圖8所示。

從圖8中可以看出，當延遲時間τ=0.5 s，τ=0.8 s和τ=1.2 s時，系統仍然可以保持穩定。但隨著延遲時間的增加，系統動態性能也隨之變差。當延遲時間為τ=1.5 s時，系統輸出最終變得發散不穩定。 由此可見，所提出的頻率控制方法，在具有時延的情況下并不保守，僅在一定的通信延時范圍內才能保證控制系統的穩定，并滿足相應的控制指標。

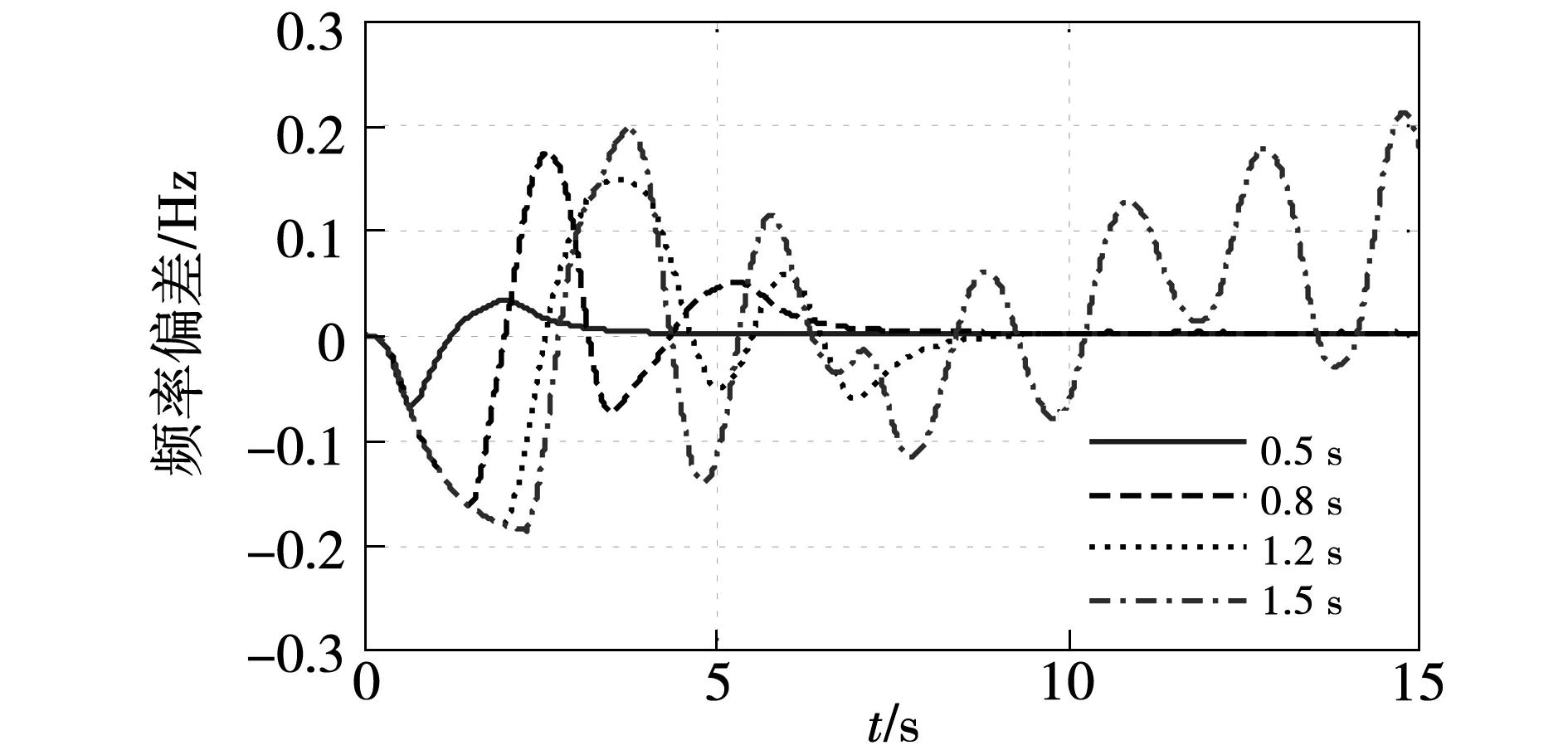
圖8 具有延時情況下微電網頻率階躍響應Fig.8 Frequency step response of time delay

3.3 具有延時與參數攝動情況下穩定性分析

系統在風、光、荷功率發生突變(ΔPwind，ΔPPV和ΔPLoad)和參數攝動的情況下，考慮通信延時τ=0.5 s時，分別對系統采用μ-H∞控制、H∞控制以及PI控制方法進行仿真比較，分析系統動態響應及頻率波動情況。

為了驗證所提的控制方法能有效平抑間歇性電源出力和負荷的隨機波動性等引起的頻率偏差，設置了四種有功功率波動場景，分別是：場景1，風電輸出功率PWP降低0.4 pu運行情況；場景2，光伏發電輸出功率PPV下降0.45 pu運行情況；場景3，負載波動PLoad上升0.06 pu運行情況；場景4，PWP下降0.3 pu，PPV上升0.3 pu，PLoad下降0.5 pu運行情況。分別對比分析采用PI控制方法、H∞控制方法和μ-H∞控制方法，其仿真運行結果如圖9所示。

從圖9(a)～圖9(d)中可以看出，間歇性電源(如風力發電、光伏發電)出力的不確定性和負荷的波動性均會使得微電網的頻率產生偏差，造成系統頻率不穩定。采用PI控制方法、H∞控制方法和μ-H∞控制方法均能使系統頻率逐漸穩定。但是采用PI控制方法，系統穩定時間達12 s，系統動態響應時間長，超調量較大。采用H∞控制方法，系統能在8 s內達到穩定；而采用μ-H∞控制方法頻率波動較小，系統在6s內就能達到穩定，相比于H∞控制方法，系統響應速度快，其超調量小。

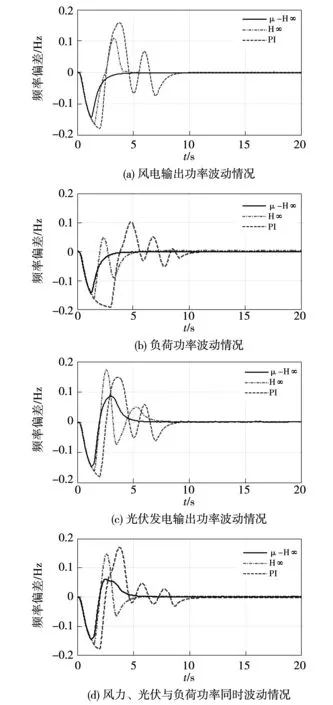
圖9 風光荷功率波動下微電網輸出頻率偏差Fig.9 Output frequency deviation of microgrid under wind,photovoltaic and load power fluctuation

綜合分析4個情景下的頻率偏差，所設計的μ-H∞控制器控制性能優于H∞控制器和傳統PI控制器，減小了調節時間，提高了系統頻率穩定性和動態性能。

為了進一步驗證所設計控制器的穩定性，搭建了一套基于Matlab/Simulink仿真軟件、dSPACE1007及其Control Desk的半實物仿真實驗平臺，實驗參數與仿真參數一致。其中，風力系統、柴油發電機、微型渦輪、燃料電池等在dSPACE1007中建模，而光伏發電則為2臺5 kW的光伏并網逆變器并聯組網系統，儲能采用30 kW磷酸鐵鋰電池。為實驗研究的方便，設定系統存在網絡延時有上界為：τmax=1.2 s。

圖10為所設計的H∞和μ-H∞控制器在系統存在風、光、荷功率波動，且存在網絡延時的情況下，系統頻率波動情況實驗結果。

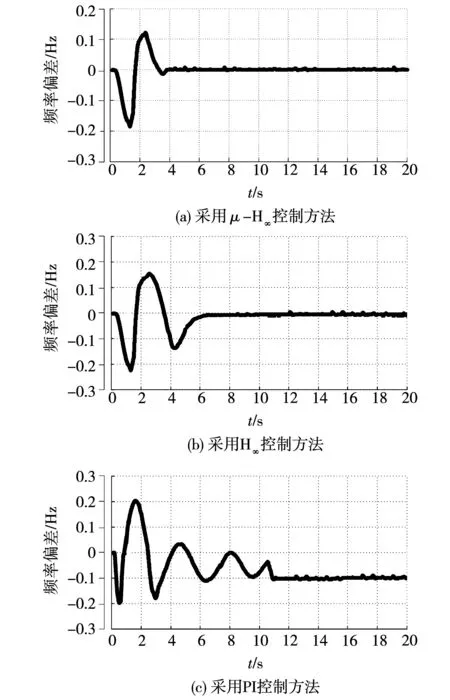
圖10 考慮延時及功率波動情況微電網頻率偏差(實驗)Fig.10 Frequency deviation of microgrid considering time delay and power fluctuation (Experiment)

從圖10中可以看出，采用H∞和μ-H∞控制方法均能使系統在較短的時間內達到穩定，頻率恢復到額定頻率值。但是兩者相比較，采用μ-H∞控制方法，系統響應速度快，動態性能較好，這與仿真結果基本吻合。而采用PI控制方法，系統無法使頻率恢復到額定頻率值，存在偏差，主要原因微電網二次頻率控制中，采用PI控制器無法解決通信延時對系統性能的影響。

4 結 論

為了解決孤島交流微電網中風力、光伏發電的輸出功率以及負荷的間歇性與波動性所引起的頻率波動問題，本文提出了一種基于μ-H∞綜合的微電網頻率控制方法。通過考慮微電網中參數攝動、結構不確定性與通信延時問題，建立了考慮通信延時的微電網頻率控制狀態空間模型，將H∞與μ綜合魯棒控制方法應用到微電網頻率控制中，所設計的控制器對一定范圍內的通信延時能夠保持系統頻率穩定。最后，通過搭建Matlab/Simulink仿真與dSPACE1007半實物仿真平臺，驗證所提控制方法的有效性與可行性。仿真與實驗結果表明，所提的μ-H∞控制方法在參數攝動、通信延時和結構不確定的情況下，系統有較好的動態性能，對微電網頻率波動有很好的平抑作用，且對一定的通信延時具有較強的魯棒性能。