電動汽車用PMSM帶濾波補償三階滑模自抗擾控制

王曉遠，劉銘鑫，陳學永,2，李小寧

(1.天津大學 電氣自動化與信息工程學院，天津 300072；2.天津內燃機研究所，天津 300072)

0 引 言

隨著全球氣候問題日益加劇，低污染、高效的電動汽車深受關注，逐漸成為研究的熱點問題。內置式永磁同步電機因其電磁轉矩大、調速范圍寬等優(yōu)點[1-3]，廣泛地應用于電動汽車驅動電機領域中。在電動汽車中常采用最大轉矩電流比(maximum torque per ampere,MTPA)控制的永磁同步電機(permanent magnet synchronous motor, PMSM)矢量控制方法。相比較于id=0控制方法，MTPA能夠充分利用電機的磁阻轉矩，從而實現(xiàn)以較小電流得到相同轉矩的目的，更符合電動汽車對于大轉矩的要求[4]。

然而，電動汽車具有運行工況復雜、干擾大等特點，因此對驅動電機的控制系統(tǒng)有著更高的要求。傳統(tǒng)應用的PI控制器無法滿足PMSM控制系統(tǒng)對高給定跟蹤性能與強抗擾能力的要求。伴隨著非線性控制理論的發(fā)展，模型預測控制(model predictive control, MPC)[5-8]、模型參考自適應控制(model reference adaptive control, MRAC)[9-10]、滑模控制(sliding mode control, SMC)[11-14]等開始被用來替代PI控制用以驅動永磁同步電機。其中，滑模控制是一種變結構控制，滑模控制函數(shù)的開關特性將系統(tǒng)的工作點限制在滑動模態(tài)上，并進一步運動到穩(wěn)定點，具有響應速度快、抗擾能力強等優(yōu)點。但滑模控制通常是使用較大的開關增益來實現(xiàn)對干擾的快速控制，這將會導致控制系統(tǒng)所不期望的抖振現(xiàn)象的發(fā)生。

針對這一問題，一些學者致力于設計新型滑模趨近律與開關函數(shù)。文獻[15]設計了一種基于新型趨近律和高階快速終端滑模觀測器的新型滑模控制方法，有效地減小了負載擾動引起的速度波動；文獻[16]提出了一種改進型變指數(shù)趨近律的滑模控制器，在一定程度上抑制了抖振；文獻[17]將一種新型的分數(shù)階滑模控制器用于永磁同步電機轉速環(huán)控制，具有較好的魯棒性。但這一類改進方法，當永磁同步電機運行于低速受到干擾時，仍存在著抖振問題。另有一些學者將滑模控制與干擾觀測器相結合，利用干擾觀測器等效估計控制系統(tǒng)內部的擾動，并利用這一估計的擾動對滑模控制器進行補償，從而減輕干擾變化對滑模控制器性能的影響[18-19]。然而，干擾觀測器的設計依賴于精確的控制模型， MTPA控制策略的數(shù)學模型較為復雜，計算量過大。

自抗擾控制[20]因其優(yōu)越的抗擾性能以及不依賴被控對象精確數(shù)學模型的優(yōu)點受到國內外學者的廣泛關注。其主要思想為將控制系統(tǒng)內部不可建模的部分與外界環(huán)境的未知干擾當作系統(tǒng)的總干擾，由擴張狀態(tài)觀測器觀測出來，進行補償以消除干擾的影響[21]。文獻[22]將自抗擾控制與滑模控制結合在了一起，無需建立精確的永磁同步電機數(shù)學模型，具有良好抗擾性能的同時減小了滑模控制所帶來的抖振影響，但其僅僅將改進技術應用于電流環(huán)，轉速環(huán)仍采用傳統(tǒng)的PI控制。文獻[23]將滑模自抗擾控制融入轉速-電流控制器的設計中，并將已知擾動與未知擾動分離以減小計算量，具有調速范圍寬、抗擾能力強的優(yōu)點。但是在電動汽車用PMSM控制系統(tǒng)中，通常會使用低通濾波器濾除由系統(tǒng)內外部產(chǎn)生的干擾在轉速環(huán)中產(chǎn)生的噪聲，將會導致轉速反饋存在相位延遲的問題。

論文采用滑模控制思想提高電動汽車用永磁同步電機控制性能，將自抗擾控制引入其中，利用低通濾波器數(shù)學模型實時補償轉速反饋信號，提出電動汽車用永磁同步電機帶濾波補償三階滑模自抗擾控制(filtered sliding mode active disturbance rejection control，F(xiàn)SM-ADRC)。為了削弱滑模控制器的抖振，避免使用最大轉矩電流比控制策略所帶來的計算模型復雜的問題，提高控制系統(tǒng)給定跟蹤能力與抗擾性能，對未知擾動的實時估計補償，提高負載擾動以及電機參數(shù)失配等情況下的轉速響應能力與抗擾性能。

1 二階滑模控制

1.1 PMSM數(shù)學模型

本文所研究的被控對象為內置式永磁同步電機，使用最大轉矩電流比控制策略。內置式永磁同步電磁轉矩表達式為

(1)

式中：p為電機極對數(shù)；ψf為轉子永磁體磁鏈；iq為q軸電流；id為d軸電流；Ld、Lq分別為d、q軸電感。

PMSM運動狀態(tài)方程與dq軸電壓方程為:

(2)

式中：TL為負載轉矩；J為轉動慣量；ω為電機角速度；B為摩擦因數(shù)；ud、uq分別為d軸與q軸電壓；R為定子電阻。

1.2 PMSM二階滑模控制器動態(tài)模型

結合PMSM運動狀態(tài)方程與電壓方程，考慮未知擾動的影響。選取角速度ω為狀態(tài)變量x1，則轉速環(huán)滑模控制器狀態(tài)方程可以設計為:

(3)

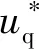
f為包含系統(tǒng)內部擾動與外部擾動的總擾動。將系統(tǒng)內部擾動fn定義為

(4)

其中：

(5)

將永磁同步電機磁阻轉矩放入總擾動中進行估計，可以降低MTPA控制策略的模型計算復雜度，節(jié)約時間成本。

PMSM轉速環(huán)控制器總擾動為

(6)

式中：ΔR為定子電阻變化量；Δψf為永磁體磁鏈變化量；ΔLd為d軸電感變化量。

定義轉速環(huán)滑模面誤差為

δ=ω*-ω。

(7)

式中ω*為電機給定角速度。

設計二階滑模控制器的滑模面為

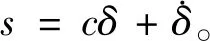
(8)

式中c>0為二階滑模控制器滑模面系數(shù)。

將系統(tǒng)總擾動考慮在內，設計控制器趨近律為

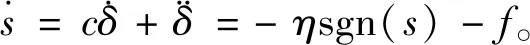
(9)

式中：sgn(·)為開關函數(shù)；η>0為開關函數(shù)增益。

此時，二階滑模控制器輸出為

(10)

1.3 二階滑模控制器收斂性分析

使用Lyapunov穩(wěn)定性驗證二階滑模控制器的穩(wěn)定性，表達式為

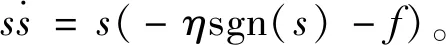
(11)

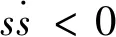
η>|f|。

(12)

2 帶濾波補償三階滑模自抗擾控制

由于未知擾動的不確定性，若二階滑模控制器保持穩(wěn)定，則需要較大的η。這將導致滑模控制器抖振加劇，不利于控制系統(tǒng)穩(wěn)定。而且，PMSM控制系統(tǒng)在使用低通濾波器濾除諧波等高頻噪聲干擾時會帶來反饋信號相位偏移，進而導致控制系統(tǒng)準確性降低。針對以上問題，本文提出一種帶濾波補償三階滑模自抗擾控制器，在二階滑模控制器的基礎上，引入自抗擾控制的思想。根據(jù)低通濾波器與PMSM數(shù)學模型構建跟蹤微分器，根據(jù)滑模面函數(shù)構建非線性狀態(tài)誤差反饋控制律，另構建改進型擴張狀態(tài)觀測器進行總擾動估計，提高PMSM系統(tǒng)控制精度。

2.1 FSM-ADRC控制器的構建

1)跟蹤微分器。

低通濾波器數(shù)學模型為

(13)

式中：ωf為濾波后電機角速度；Tω為低通濾波器時間常數(shù)。

基于低通濾波器數(shù)學模型與PMSM二階滑模控制器方程，令狀態(tài)變量xq1=ωf，構建的帶濾波補償三階滑模自抗擾控制器跟蹤微分器為：

(14)

式中：K=kt/Tω為跟蹤微分器系數(shù)；FSM-ADRC控制器已知擾動fyq=-K(Riq+ωfLdid+ωfψf)。

FSM-ADRC控制器總擾動為

(15)

內部擾動為

(16)

其中：

(17)

2)非線性狀態(tài)誤差反饋控制律。

基于滑模控制器模型構建非線性狀態(tài)誤差反饋控制律，定義FSM-ADRC滑模面誤差為

δq=ω*-ωf。

(18)

基于跟蹤微分器模型設計FSM-ADRC的滑模面為

(19)

式中：cq1與cq2為FSM-ADRC滑模面系數(shù)，且cq1>0，cq2>0。

為使控制器可以收斂于穩(wěn)定狀態(tài)，設計滑模面趨近律為

(20)

式中ηq> 0為FSM-ADRC開關增益。

此時，F(xiàn)SM-ADRC輸出為

(21)

與二階滑模控制器相同，為使系統(tǒng)收斂，F(xiàn)SM-ADRC也需要較大的開關增益。

為解決此問題，本文使用改進型擴張狀態(tài)觀測器進行擾動估計，補償?shù)娇刂破鬏敵鲋校瑯O大地減小滑模控制器開關增益。

3)改進型擴張狀態(tài)觀測器的構建。

(22)

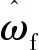
三只松鼠股份有限公司2012年12月成立于安徽蕪湖，主要從事于堅果類、茶類和休閑零食類等食品的新興互聯(lián)網(wǎng)企業(yè)，整個業(yè)務流程涉及產(chǎn)品的研發(fā)、分裝和銷售，并在淘寶天貓商城上線65天后就成為了中國堅果類電商食品第一名，是中國第一家純互聯(lián)網(wǎng)食品品牌企業(yè)。三只松鼠的成功有其獨特之處，通過對其創(chuàng)業(yè)方式、營銷手段和企業(yè)文化等方面的探討研究，為其他同類型企業(yè)的發(fā)展提供借鑒。

(23)

式中rq>0為轉速環(huán)改進型擴張狀態(tài)觀測器擾動增益。

另，將FSM-ADRC滑模面趨近律替換為

(24)

此時，控制器的輸出為

ηqsgn(sq)]/K。

(25)

2.2 FSM-ADRC控制器穩(wěn)定性分析

為驗證FSM-ADRC收斂性能，所構建的Lyapunov函數(shù)為

(26)

則

(27)

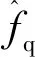
(28)

則

(29)

此時，只要ηq選取任意大于0的值均可使控制系統(tǒng)穩(wěn)定，極大地削弱了滑模控制器的抖振現(xiàn)象。三階FSM-ADRC控制器結構框圖如圖1所示。

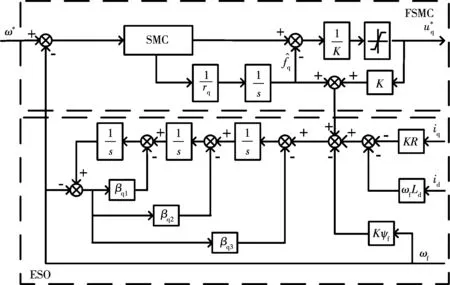
圖1 三階FSM-ADRC控制器結構框圖Fig.1 Structure block diagram of third order FSM-ADRC controller

2.3 d軸電流環(huán)控制器的構建

在d軸電流環(huán)中，采用一階滑模自抗擾控制器(sliding mode active disturbance rejection control， SM-ADRC)。

1)跟蹤微分器。

令狀態(tài)變量xd1=id，基于d軸電壓方程構建的d軸電流環(huán)跟蹤微分器為

(30)

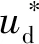
已知擾動fyd為

(31)

未知擾動fd為

(32)

2)非線性狀態(tài)誤差反饋控制律。

定義d軸電流環(huán)滑模面誤差為

(33)

設計d軸電流環(huán)控制器滑模面為

(34)

式中cd>0為d軸電流環(huán)滑模面系數(shù)。

設計d軸電流環(huán)滑模面趨近律為

(35)

式中ηd>0為d軸電流環(huán)滑模面開關增益。

此時，d軸電流環(huán)控制器輸出為

(36)

式中

(37)

3)改進型擴張狀態(tài)觀測器的構建。

將d軸電流環(huán)改進型擴張狀態(tài)觀測器的誤差定義為

(38)

改進型d軸擴張狀態(tài)觀測器方程為：

(39)

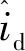
將式(35)改為

(40)

改進后的SM-ADRC控制器輸出為

(41)

一階SM-ADRC控制器結構框圖如圖2所示。

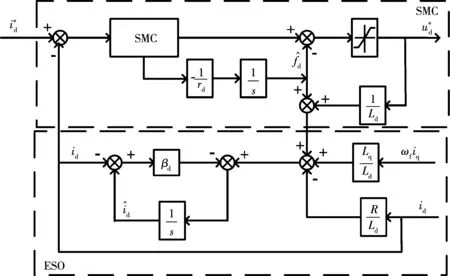
圖2 一階SM-ADRC控制器結構框圖Fig.2 Structure block diagram of first order SM-ADRC controller

3 仿真分析與實驗驗證

電動汽車用內置式永磁同步電機帶濾波補償三階滑模自抗擾控制系統(tǒng)結構圖如圖3所示。為驗證本文所提控制方法的有效性，針對永磁同步電機控制系統(tǒng)分別做了仿真與實驗驗證。仿真與實驗所用的永磁同步電機參數(shù)如表1所示。

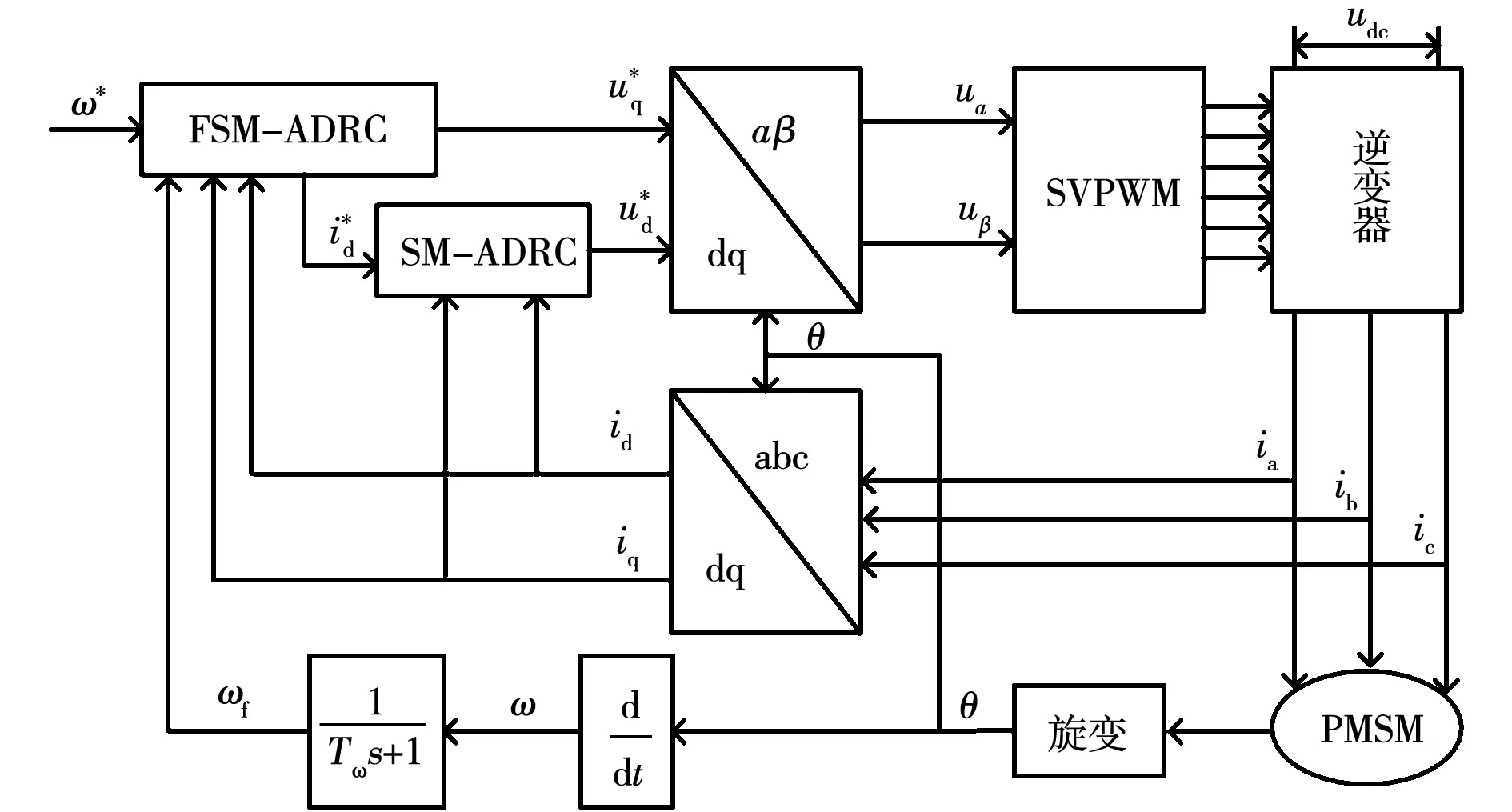
圖3 FSM-ADRC控制系統(tǒng)結構框圖Fig.3 Structure block diagram of FSM-ADRC control system

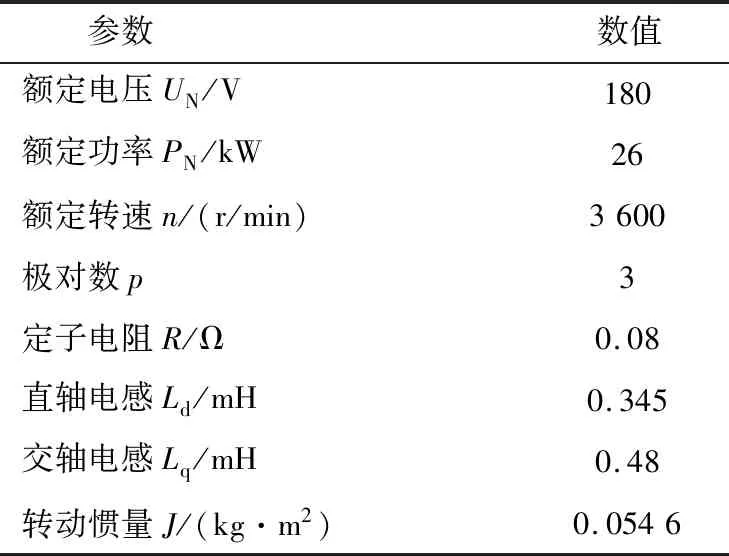
表1 仿真與實驗用PMSM參數(shù)Table 1 PMSM paraments used in simulation and experiment

3.1 仿真分析

為測試FSM-ADRC控制系統(tǒng)抗負載擾動能力，設置控制系統(tǒng)給定轉速為1 200 r/min，負載轉矩由最初的空載狀態(tài)到0.4 s時突增至50 N·m，上述三種控制策略抗負載擾動性能與給定跟蹤誤差對比如圖4所示。

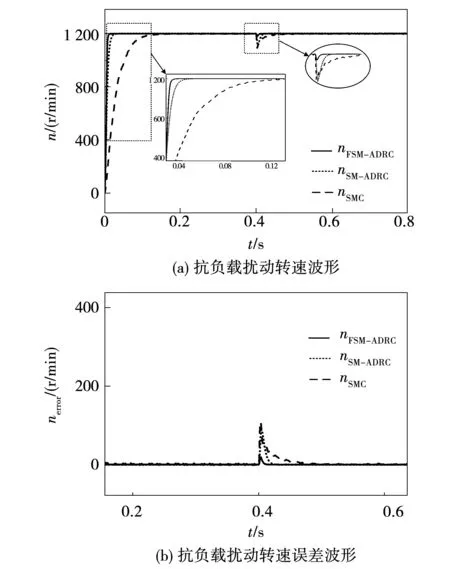
圖4 抗負載擾動轉速仿真波形Fig.4 Anti load disturbance speed simulation waveform

三種控制方法在負載擾動時性能對比如表2所示。可以看到，F(xiàn)SM-ADRC控制方法相較于SMC與SM-ADRC控制方法更快地到達給定轉速1 200 r/min，無抖振現(xiàn)象，且在50 N·m的負載擾動時轉速最大跌落為30 r/min，誤差僅為2.5%。

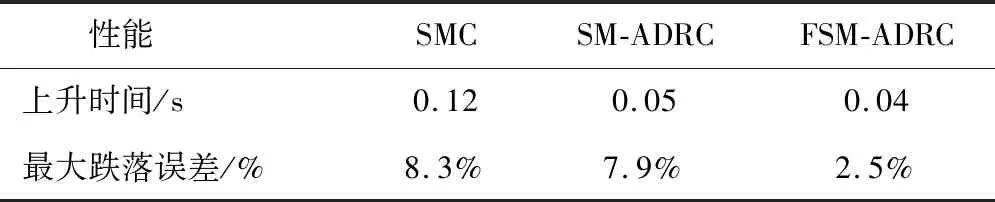
表2 三種控制方法在負載擾動時性能對比表Table 2 Performance comparison table of three control methods under load disturbance

為測試電動汽車用永磁同步電機FSM-ADRC控制器的給定跟蹤能力，分別給予控制系統(tǒng)正弦與三角給定轉速，對比滑模控制方法、滑模自抗擾控制方法以及本文所提出的帶濾波補償滑模自抗擾控制方法，得到三種控制方法的正弦給定與三角給定跟蹤轉速與誤差波形分別如圖5與圖6所示。

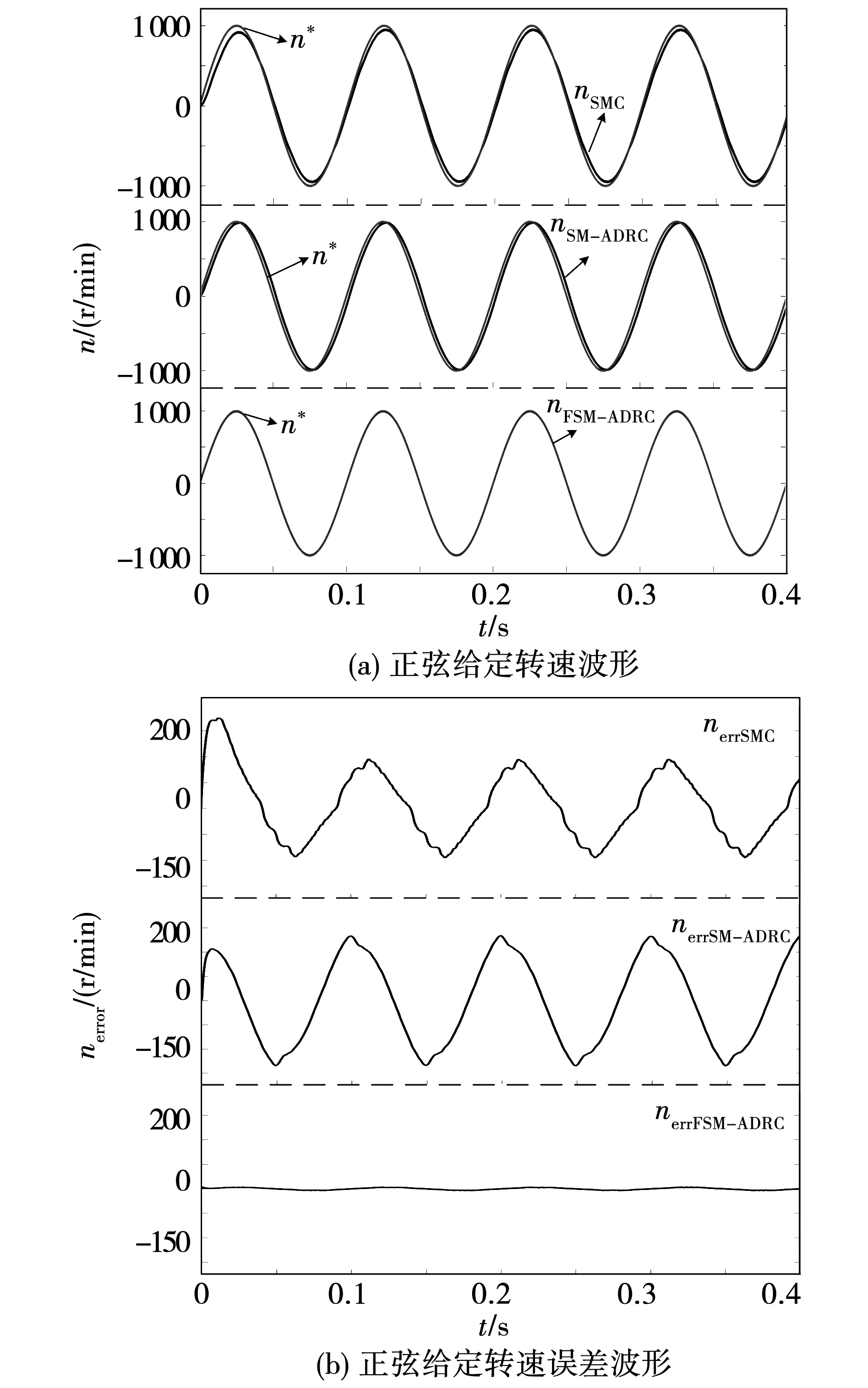
圖5 正弦給定轉速仿真波形Fig.5 Sine given speed simulation waveform

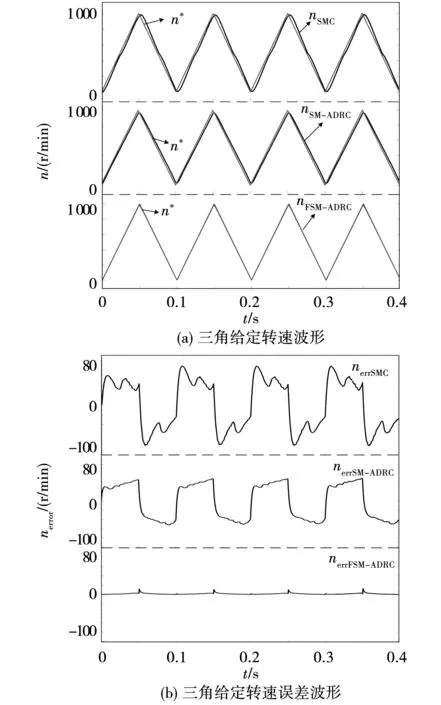
圖6 三角給定轉速仿真波形Fig.6 Triangle given speed simulation waveform

可以看到，跟蹤正弦與三角給定時，F(xiàn)SM-ADRC方法由于進行了濾波補償，相對于SMC與SM-ADRC控制方法具有更精準的給定跟蹤能力，跟蹤誤差較小，幾乎沒有幅值衰減與相位偏移問題。正弦給定與三角給定相對于階躍給定而言更加難以跟蹤， 因此可以證明FSM-ADRC具有很好的跟蹤精度，可以滿足電動汽車對于實時準確跟蹤的需求。

由于電動汽車在復雜工況下行駛易導致電機內部參數(shù)的變化，為測試FSM-ADRC控制方法對電機參數(shù)變化的敏感性，在參數(shù)失配情況下進行負載擾動實驗。

圖7為給定轉速1 200 r/min、0.4 s突增50 N·m負載情況的參數(shù)失配時三種方法永磁同步電機抗負載擾動轉速波形。三種方法在電機參數(shù)失配情況下性能對比如表3所示。

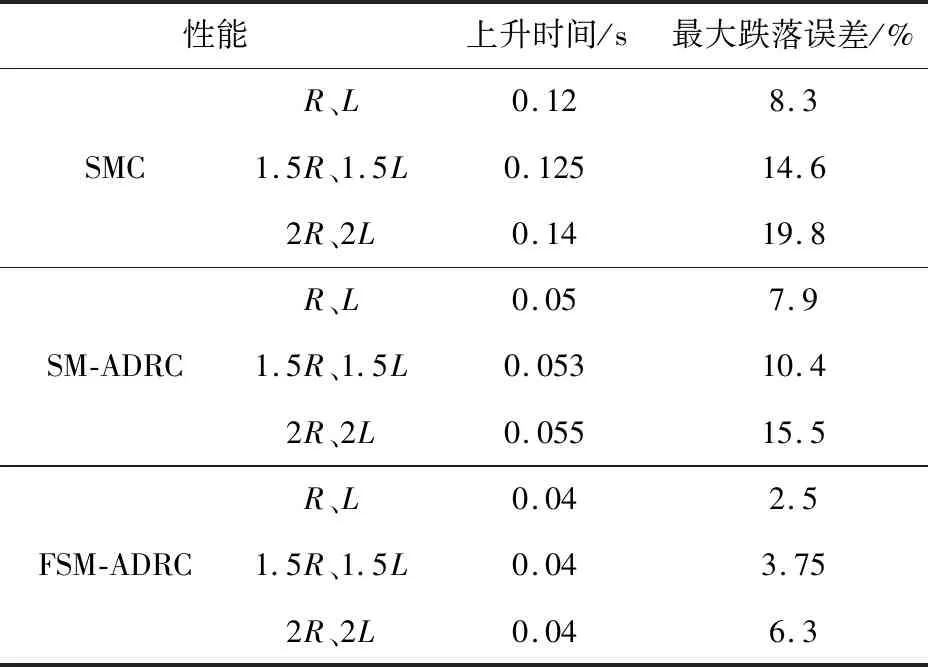
表3 三種控制方法參數(shù)失配負載擾動時性能對比表Table 3 Performance comparison of three control methods anti-load disturbance speed with motor parameter change

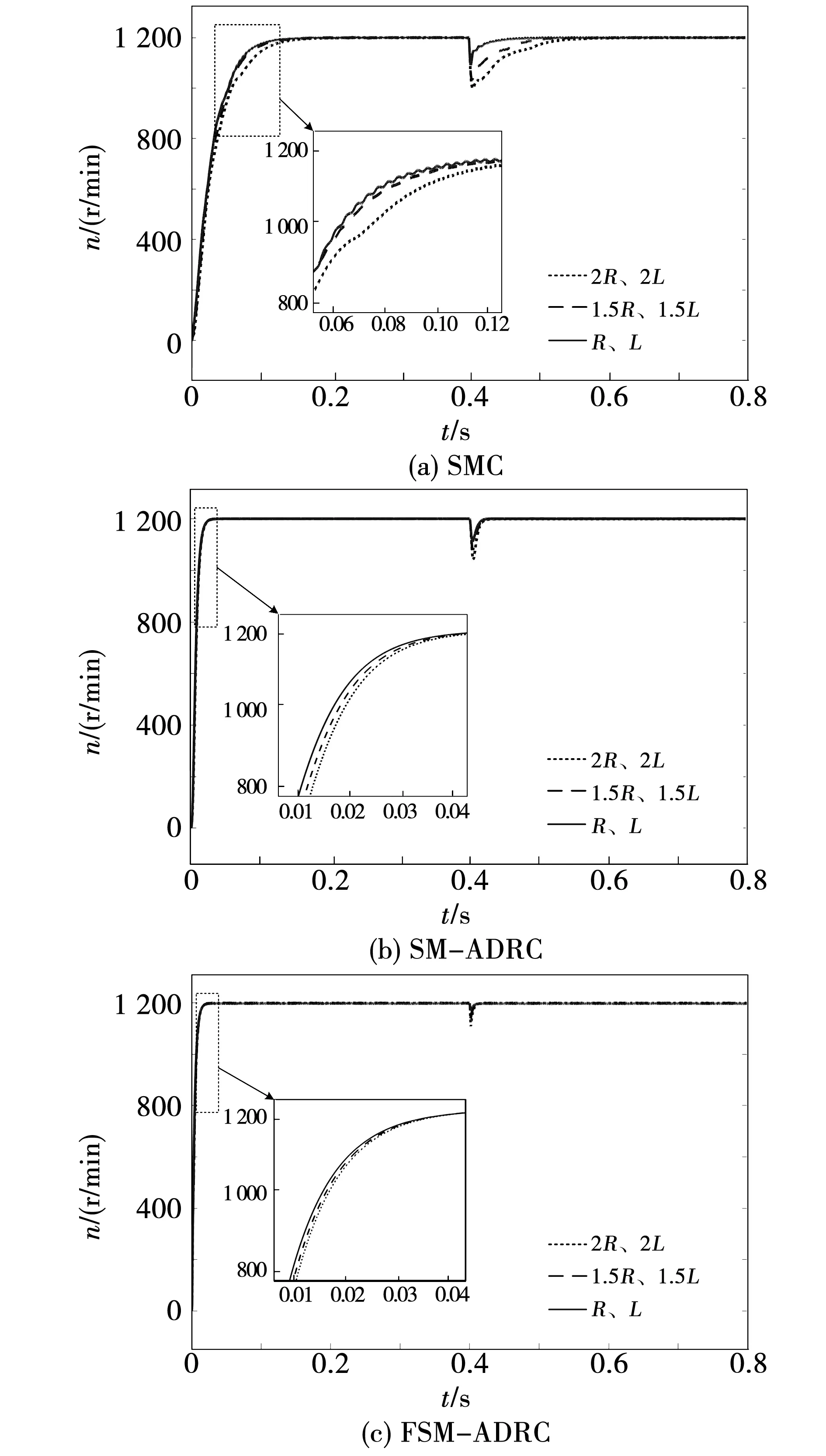
圖7 三種方法電機參數(shù)失配抗負載擾動轉速仿真波形Fig.7 Three methods anti-load disturbance speed with motor parameter change speed simulation waveform

與SMC與SM-ADRC控制方法相比，電機參數(shù)失配情況下，F(xiàn)SM-ADRC控制方法的轉速上升時間基本未變，轉速最大跌落誤差雖略有增加，但相比較于SMC控制方法與SM-ADRC控制方法在電阻、電感值增加100%時，轉速最大跌落誤差分別增大11.5%與7.6%相比，F(xiàn)SM-ADRC控制方法僅增大3.8%，可以相對更加快速地回歸穩(wěn)定狀態(tài)，對電機參數(shù)變化的敏感度較低。

圖8為永磁同步電機參數(shù)失配時FSM-ADRC控制系統(tǒng)正弦與三角給定轉速跟蹤仿真波形。FSM-ADRC在參數(shù)變化前后均保持很強的給定跟蹤能力，誤差值很小。由此可見，F(xiàn)SM-ADRC永磁同步電機控制系統(tǒng)對參數(shù)變化的敏感性較低。

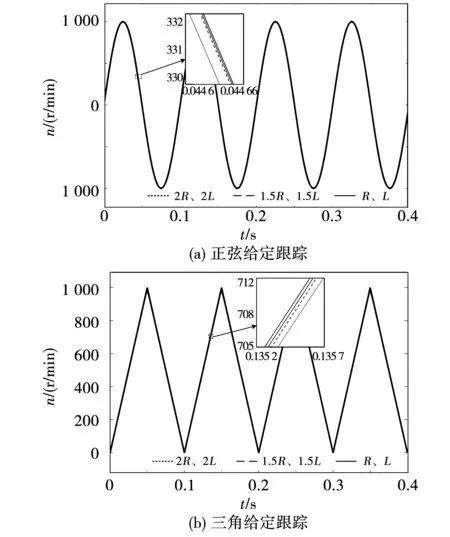
圖8 正弦及三角給定轉速仿真波形Fig.8 Sine and triangle given speed simulation waveform

仿真結果表明，本文所提的FSM-ADRC永磁同步電機控制系統(tǒng)具有良好的魯棒性，相對于SMC與SM-ADRC具有更加良好的給定跟蹤能力與抗負載擾動性能。

3.2 實驗驗證

為進一步驗證所提方法，所用的實驗平臺如圖9所示。

圖9 實驗平臺Fig.9 Experimental platform

設定給定轉速為1 100 r/min、空載啟動，分別使用三種控制方法的永磁同步電機抗負載擾動轉速實驗波形如圖10所示。可以看到，F(xiàn)SM-ADRC控制方法比SMC控制方法具有更加快速的動態(tài)響應能力。而且，相比較于其他兩種控制方法，F(xiàn)SM-ADRC在負載突變時的轉速波動更小，抗負載擾動能力更優(yōu)。

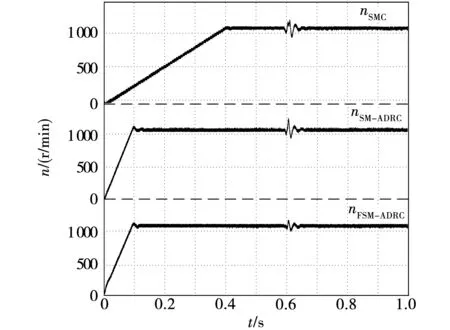
圖10 抗負載擾動轉速實驗波形Fig.10 Anti load disturbance speed experimental waveform

為在實驗中驗證SMC、SM-ADRC與FSM-ADRC控制器在電機參數(shù)失配時的電機敏感性，分別設置三種控制器中的電阻與電感量為實際值的兩倍。由圖11所示，當電機參數(shù)失配時SMC與SM-ADRC控制器抗擾性能均有明顯降低，其中SMC控制器電機參數(shù)失配時轉速最大跌落誤差與原來相比增加了12.8%，SM-ADRC增加了8.4%。而FSM-ADRC控制器性能幾乎沒有變化，與電機未失配時相比僅增加了4%。由此可見，F(xiàn)SM-ADRC永磁同步電機控制系統(tǒng)對電機參數(shù)變化不敏感，可以適用于多種復雜工況。

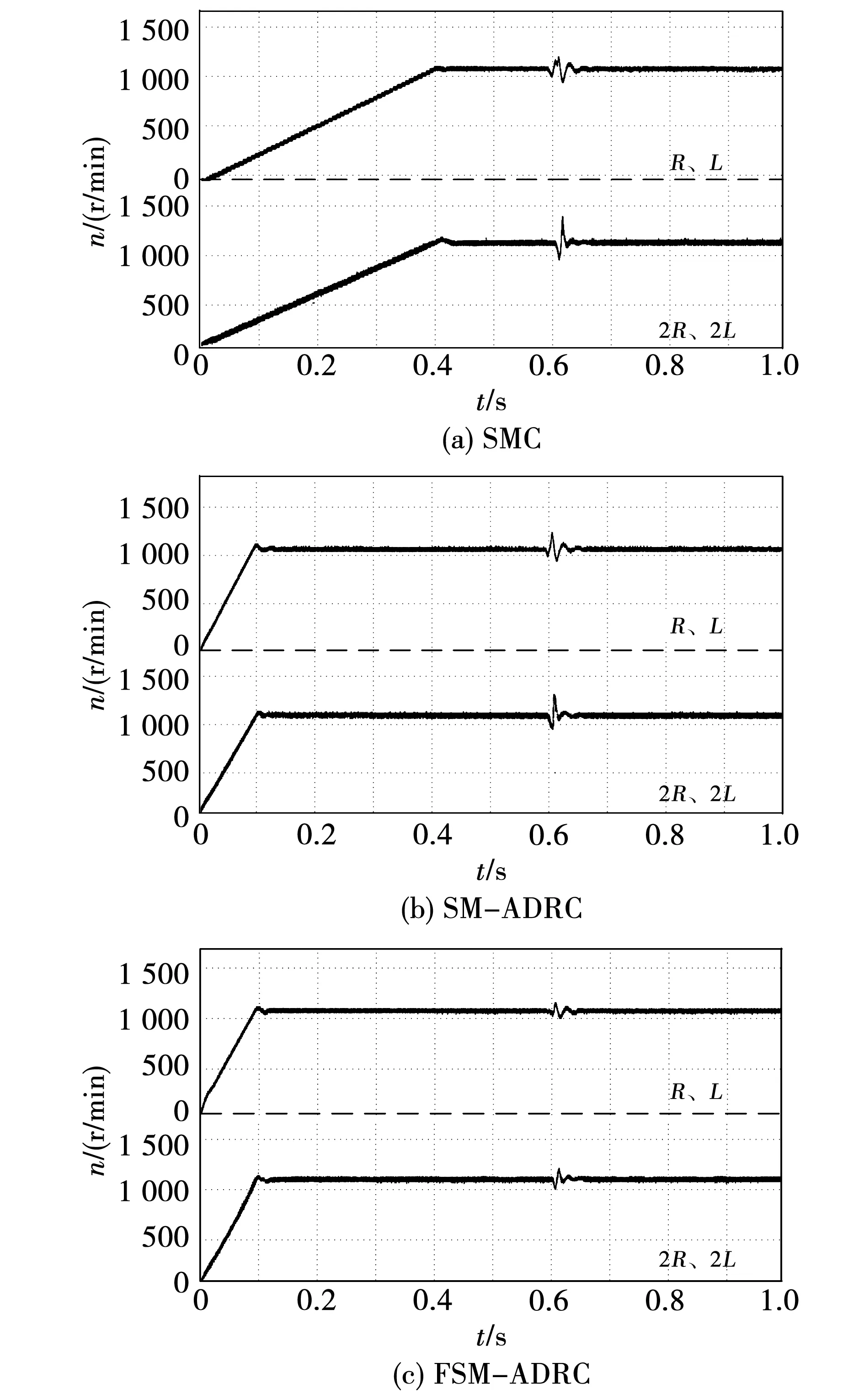
圖11 電機參數(shù)失配三種方法抗負載擾動轉速實驗波形Fig.11 Three methods anti-load disturbance speed with motor parameter change speed experimental waveform

實驗結果表明，本文所提的帶濾波補償滑模自抗擾控制方法的抗擾性能強、參數(shù)敏感性低，可以顯著提升電動汽車用永磁同步電機控制系統(tǒng)性能。

4 結 論

針對電動汽車用永磁同步電機存在的復雜工況下控制系統(tǒng)抗擾性能降低以及跟蹤能力變差的問題，本文提出了永磁同步電機帶濾波補償三階滑模自抗擾控制方法，經(jīng)過補償后，滑模控制器的抖振問題有了明顯改善，控制系統(tǒng)的抗擾性能顯著提升。仿真與實驗表明，與采用SMC與SM-ADRC的永磁同步電機控制系統(tǒng)相比，采用FSM-ADRC的控制系統(tǒng)具有更良好的魯棒性，適用于對精度要求更高的控制領域。