基于本地電壓比瞬量的直流短路故障檢測與定位方法研究
王靜,孫謙浩,劉國偉,趙宇明,代少君,熊天龍
(1.深圳供電局有限公司,廣東深圳 518020;2.清華大學電機工程與應用電子技術系,北京 100084;3.國網湖北省電力有限公司武漢供電公司,湖北武漢 430013;4.清華四川能源互聯網研究院,四川成都 610042)
0 引言
可再生能源的充分利用是解決環境污染問題與實現能源可持續發展的關鍵與核心[1]。然而,由于自身屬性的影響,可再生能源在交流電網中的并網調度與消納較為困難[2]。鑒于此,具有接入可靠、遠距離輸電成本低、運行方式多樣等優點的基于模塊化多電平換流器(Modular Multilevel Converter,MMC)的直流輸配電網在可再生能源利用領域備受關注[3],[4]。尤其是與直流線路短路故障相關的研究,目前已經成為了可再生能源直流外送領域的研究熱點之一[5],[6]。
直流線路短路故障檢測、定位、切除及恢復的主要難題在于直流故障發展的快速性[7],[8]。應用于直流線路故障檢測與定位的方法主要有突變量識別法、縱聯保護法和行波保護法。其中:突變量識別法主要以故障時幅值或變化率發生突變的量為依據對故障進行判定[9]~[12];縱聯保護法利用故障時直流線路兩端的電氣量差異對故障進行檢測與定位[13],[14],其正確性不僅易受直流線路分布式電容的影響[6],且需要進行通信。縱聯保護的快速性在直流故障判定領域面臨著一定的挑戰[8];行波保護法主要利用故障發生時暫態行波的相關信息對故障的位置進行判斷[15],[16]。目前,行波保護存在著波頭易畸變、隨時間衰減及難以捕捉等不足。
鑒于上述現狀,為了更有效地實現對連接于MMC的直流線路的短路故障檢測與定位,本文提出了一種基于故障限流電抗器電壓比瞬時值的故障檢測與定位方法,并進行了詳細的分析。基于MATLAB/Simulink仿真軟件對所提方法的正確性與有效性進行了驗證。
1 與MMC相連的直流線路故障特性分析
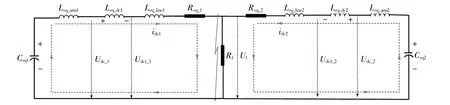
圖1為連接于MMC的直流線路通用結構及其故障等效電路。圖1(a)中,MMC換流器采用了傳統的半橋結構,每個橋臂均包含N個子模塊,為了能夠減小直流電流紋波并降低直流故障電流的上升速率,在MMC的正負極直流母線出口處分別配備了直流故障限流電感Ldc。

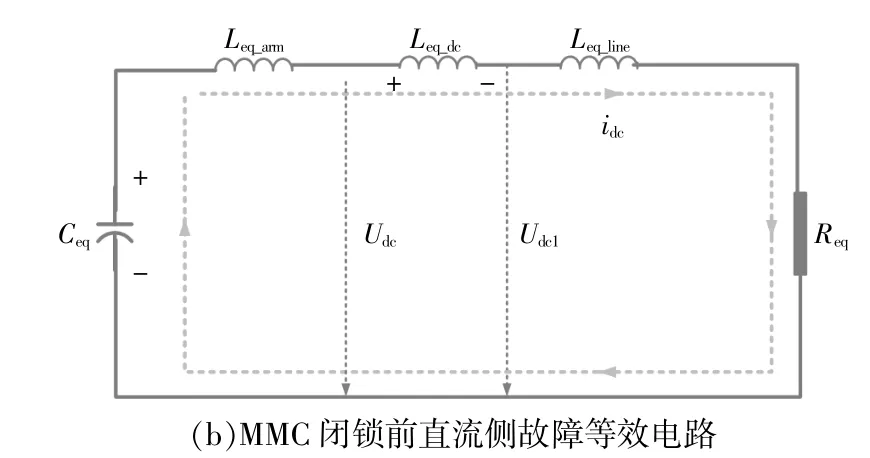
圖1 連接于MMC的直流線路通用結構及其故障等效電路Fig.1 Fault equivalent circuit and general topology of DC line connected with MMC terminal
當直流線路發生故障時,故障電流快速增加,為了保護開關器件,閉鎖MMC。鑒于此,MMC的故障行為可以分為閉鎖前與閉鎖后兩種狀態。圖1(b)給出了雙極故障發生后MMC閉鎖前的直流側故障等效電路。此時,故障回路中的等效電感Leq、等效電阻Req以及等效電容Ceq計算式分別為
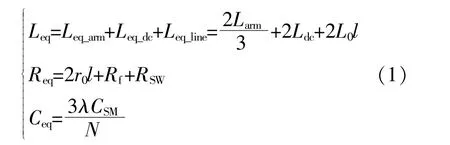
式中:r0,L0分別為線路單位長度電阻、電抗值;l為故障點的距離;Rf為故障過渡電阻;RSW為MMC中開關器件的等效電阻;CSM為橋臂各子模塊的電容值;λ為MMC橋臂電容投切造成的等效系數,取值為[1,2];Larm為MMC橋臂電感的實際值;Ldc為MMC直流側所連接的直流故障限流電感實際值;Leq_arm為MMC橋臂電感在直流側的等效值;Leq_dc為MMC直流側所連接的直流故障限流電感在直流側的等效值;Leq_line為故障點到MMC直流端口的線路等效電感值。
基于圖1(b)與式(1),直流故障發生后MMC閉鎖前,與MMC相連的直流線路的電路方程為

假設直流線路雙極故障的發生時刻為0+,則故障發生后MMC閉鎖前的電容電壓與故障電流(故障電流的交流分量在此階段由于三相橋臂的能量平衡并不會流入直流側[10],[11],而只會增加橋臂中各開關器件的流通電流)可以計算為

根據圖1(b)可知,故障限流電抗器兩端的直流電壓Udc與Udc1在直流故障后MMC閉鎖前的表達式分別為

當保護系統檢測到故障后,將會閉鎖MMC,此后MMC將進入電感單向放電階段與交流側不控整流階段[10]。由于閉鎖后的故障狀態與本文的內容相關性較小,因此不再贅述。
2 基于本地電壓比瞬時值的故障檢測與定位方法原理分析
2.1 基于本地電壓比瞬時值的故障檢測方法及故障判據整定分析
基于式(6),當直流線路發生短路故障后,在MMC閉鎖前,故障限流電感的直流電壓比瞬時值RIV(t)為

故障發生時刻0+直流電壓比瞬時值RIV(0+)為

也就是說,式(8)中的第2項通常遠小于第一項。同時,考慮到穩態運行時故障限流電感兩端的直流電壓比瞬時值穩定在1附近,而故障發生時刻的直流電壓比瞬時值RIV(0+)將小于1,因此基于本地電壓比瞬時值的故障判據與整定值應為
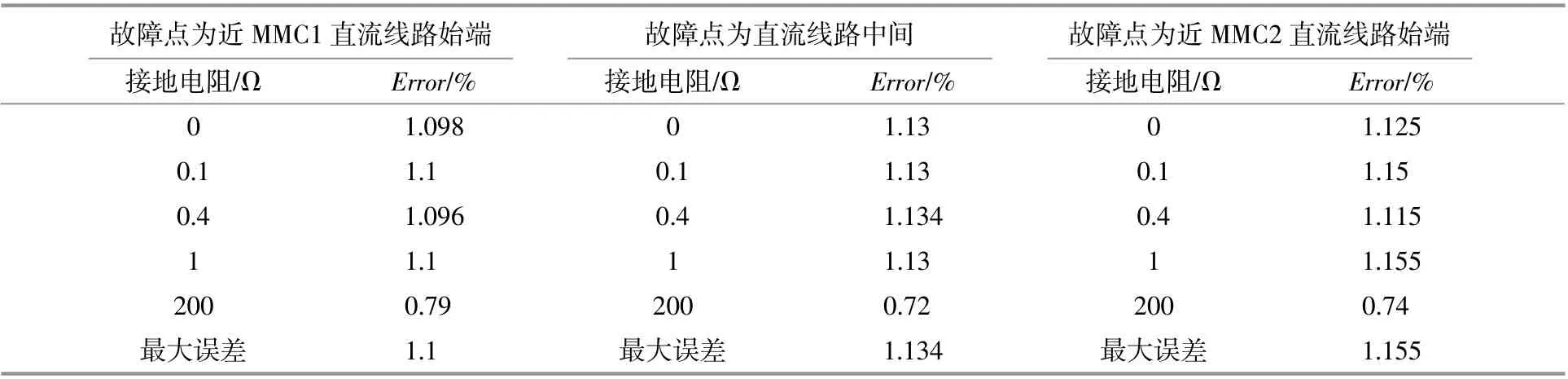
故障判據:RIV_m 式中:RIV_m,RIV_set分別為故障限流電感兩端直流電壓比瞬時值的測量值、整定值;K_set為所提故障檢測方法的整定系數,通常為大于1的常數(應避開穩態時直流側電流諧波所引起的故障限流電抗器電壓降);lline為與MMC相連的直流線路總長度;IN_MMC,UdcN_MMC分別為與直流線路相連的MMC的額定運行電流、電壓。 基于式(8),(9),連接于單端MMC的直流線路由于實際參數的限制,式(8)中的第二項可以忽略。在故障發生時刻,故障限流電抗器兩端的直流電壓比瞬時值的測量值可以簡化為 從而可以求得連接于單端MMC的直流線路的故障點與直流母線之間的距離為 由于式(12)中Ldc與L0均為已知值,因此對于連接于單端MMC的直流線路,在本文所提的方法中,根據故障發生時刻的本地電壓比瞬時值的測量值,即可計算出故障點的位置。 在包含兩端MMC的直流系統中,當直流線路發生故障時,其等效電路如圖2所示。 圖2 雙端MMC系統的直流故障等效電路Fig.2 DC fault equivalent circuit of two-terminal system based on MMC 與式(7)相似,MMC兩端直流系統直流線路故障時,可以得到兩端的電壓比瞬時值分別為 對比式(12)與式(17)可知,不同于單端MMC系統中所提基于本地電壓比瞬時值的故障定位方法會受到過渡電阻的微弱影響,在兩端MMC直流系統中,所提方法可以有效地消除過渡電阻的影響,并簡化故障定位的計算流程。 為了對所提故障檢測方法以及故障定位方法進行驗證,在MATLAB/Simulink仿真平臺中搭建了一個兩端均為±10 kV/2 MVar MMC換流器的直流輸電工程模型,系統結構如圖3所示,具體參數如表1所示。 表1 仿真參數Table 1 The table of simulation parameters 采用整定系數K_set=1.3,根據式(10)及表1的參數,可以得到兩端MMC的整定值RIVset均為0.6 6。 為了對所提故障定位方法進行驗證,本文采用以下指標對所提方法的精度進行驗證: 圖4給出了直流線路不同位置故障(F1,F2,F3)時,本地電壓比瞬時值的測量值的變化。1.2 s前,直流系統工作在額定狀態,此時MMC1控制直流電壓穩定在±10 kV,MMC2控制功率為2 MW(直流電流為0.1 kA);1.2 s后,由于故障位置的不同,電壓比瞬時值的變化規律也不同。 在圖4(a)中,故障發生在F1處,當沒有過渡電阻時,MMC1的本地電壓比瞬時值在故障發生時刻(1.2 s)將降為0,同時MMC2的本地電壓比瞬時值約為0.5,二者均明顯小于自身的整定值0.6 6。也就是說,當F1處的故障無過渡電阻時,MMC1與MMC2均只依賴本地電壓比瞬時值即可保護直流線路全長。同時,當過渡電阻為1Ω時,MMC1與MMC2的電壓比瞬時值的測量值與無故障電阻時基本相同,說明了單端測距近似簡化理論分析的正確性。 在圖4(b)中,故障發生在F2處,MMC1與MMC2的本地電壓比瞬時值在故障發生時刻(1.2 s)將降為0.33左右,二者也均明顯小于整定值0.6 6,說明了所提故障檢測方法在F2處故障時的有效性。 圖4 直流線路不同位置發生雙極故障時所提故障檢測方法的仿真驗證Fig.4 Simulation verification of the proposed fault detection method for the different fault points of DC line 在圖4(c)中,故障發生在F3處,MMC1的本地電壓比瞬時值在故障發生時刻(1.2 s)將降為0.5,MMC2的本地電壓比瞬時值約為0,說明了所提故障檢測方法在F3處故障時的有效性。 綜合上述分析,無論故障發生在直流線路的何處,MMC1與MMC2均只依靠本地電壓比瞬時值的變化即可檢測出整條線路的故障。同時,依據故障瞬間的電壓比瞬時值的測量值,基于式(17)可以確定故障點的位置。表2給出了不同位置故障時,基于式(17)的故障定位方法的計算值與實際故障位置的定位誤差。 表2 故障定位精度仿真驗證Table 2 The simulation verification of fault location precision 由表2可知,無論故障點在線路的何處,本文所提的故障定位方法的故障精度均不受故障過渡電阻的影響,且最大的定位誤差不超過1.2%,說明了所提定位方法對故障過渡電阻參數的不敏感性以及定位的準確性。 為了更快速、有效、經濟地對直流線路故障進行檢測與定位,本文提出了一種基于故障限流電抗器兩端直流電壓比瞬時值的故障保護方法,并對其進行了分析與仿真驗證。所提方法的主要特點如下: ①無需通訊設備,僅依賴本地電壓比信息即可完成對直流線路全長的保護,對采樣率的要求較低,保護系統更加具有經濟性; ②由于判斷依據為故障發生時的電壓比瞬時值的測量值,因此可以快速地對故障進行判定,保證系統的故障處理時間; ③利用故障發生時的電壓比瞬時值的測量值,可以對單端系統及雙端系統的直流故障進行精確的定位,且定位精度不受故障過渡電阻的影響。
2.2 基于本地電壓比瞬時值的故障定位方法
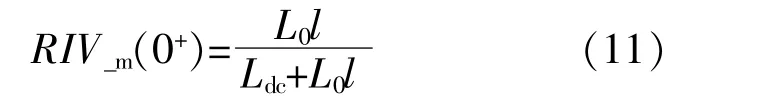
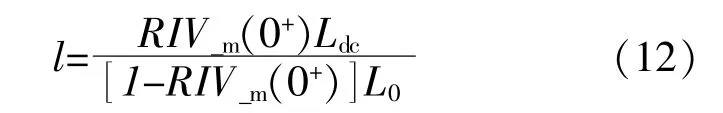


3 仿真驗證及分析




4 結論

