虛擬同步發電機參數自適應控制策略

程國棟,邵宣,王貴峰

（1.中國礦業大學徐海學院，江蘇徐州 221008；2.中國礦業大學電氣與動力工程學院，江蘇徐州 221008；3.江蘇師范大學電氣工程及自動化學院，江蘇徐州 221008）

0 引言

隨著配電網中可再生能源的發電占比逐年提高，大量逆變器接入到電力系統中，這導致電力系統的總慣性下降、穩定性受到嚴重影響[1]，[2]。利用虛擬同步發電機（Virtual Synchronous Generator，VSG）控制技術，可以為微電網提供類似同步發電機的慣性和阻尼特性，進而維持逆變器輸出頻率和功率的穩定[3]，[4]。

VSG并不是真正物理上的機械慣量，但VSG的虛擬慣量和阻尼靈活可變，可采用參數自適應的控制策略來提高VSG的運行性能。文獻[5]提出一種自適應慣性控制策略，根據不同的工況實現功率調節與頻率調節之間的平衡，同時給出了參數的設計原理，確定自適應的范圍。文獻[6]考慮外界頻率波動對系統的沖擊，分析配電網頻率突變時，不同轉動慣量對逆變器輸出頻率的影響，設計合適的慣性控制策略，實現頻率的快速響應。文獻[7]在多VSG并聯的微電網中提出改進的轉動慣量自適應控制，有效抑制了并聯VSG帶來的功率振蕩，但其并未考慮阻尼變化對系統的影響。文獻[8]提出一種自適應控制策略，在運行過程中使系統保持最佳阻尼比，用以優化超調以及響應時間等指標，進而抑制頻率和功率的振蕩，提高了VSG的動態性能。文獻[9]提出一種使用模糊邏輯的自適應虛擬慣性控制方法，以保證系統在高滲透條件下運行所需的頻率穩定性。該方法根據有功功率和系統頻率偏差自動調整虛擬慣性常數，避免了參數選擇不當，實現了快速的慣性響應。文獻[10]根據負載擾動情況改變轉動慣量的大小，進而調節系統的頻率響應，但其并未給出轉動慣量的具體表達式。

上述文獻均只對轉動慣量進行自適應控制，沒有考慮阻尼系數的影響。本文提出一種基于模糊控制的雙參數自適應控制策略。通過分析VSG的功角特性，確定轉動慣量和阻尼系數的選取原則；根據角速度偏差量及其變化率來確定模糊規則，實現轉動慣量和阻尼系數的自適應調節，進而抑制頻率和有功功率的波動，提高系統的動態性能。

1 虛擬同步發電機的數學模型

虛擬同步發電機的控制框圖如圖1所示。系統主控部分為三環控制。外環為VSG功率控制環，是VSG控制的核心部分，由頻率控制和電壓控制組成，提供電壓和頻率支撐；內環為雙閉環控制，用以穩定VSG的輸出電壓，提高系統抗擾性能，加快電流動態響應。將雙閉環輸出的電壓信號傳送到SVPWM調制環節，便得到開關管的驅動信號。

圖1 虛擬同步發電機的控制框圖Fig.1 Control block diagram of VSG

VSG的頻率控制可通過轉子運動方程實現。為便于逆變器的控制，對同步發電機的模型進行降階處理，采用經典二階模型對虛擬同步發電機進行建模，可得轉子運動方程為

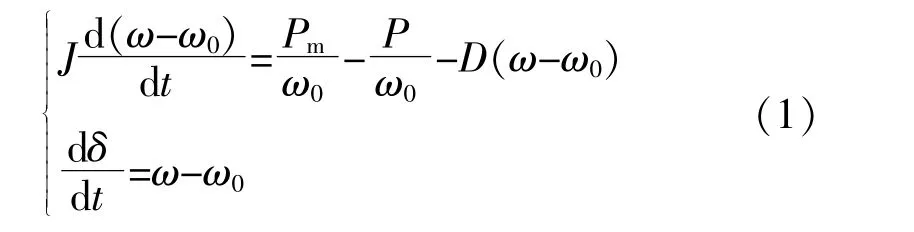
式中：J為轉動慣量；ω為轉子角速度；ω0為額定角速度；Pm為VSG機械功率；P為VSG輸出功率；D為阻尼系數；δ為VSG的功角。

轉子運動方程通過模擬轉矩的不平衡來實現轉子的加速和減速，虛擬轉動慣量J可抑制頻率的波動，阻尼系數D可增強系統的抗擾能力。根據同步發電機的無功調壓特性，可得到VSG的電壓控制方程為

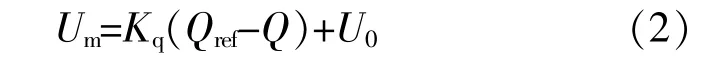
式中：Um為系統電壓參考值；U0為額定電壓；Q為VSG的無功功率；Qref為無功功率指令值；Kq為無功下垂系數。

在下垂控制基礎上，加入勵磁調節控制，用于維持VSG輸出電壓的穩定，勵磁調節控制方程為

式中：E為勵磁電動勢；ki為積分系數；U為VSG實際輸出電壓。

由式（1）和式（3）可得VSG的控制框圖，如圖2所示。

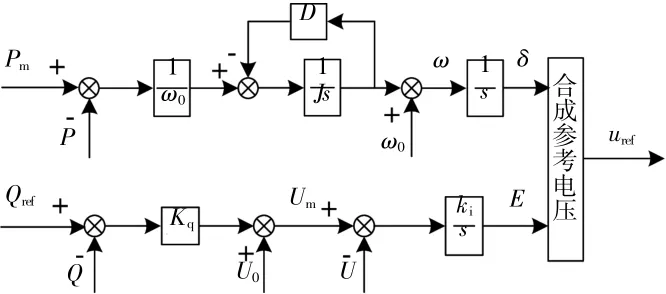
圖2 VSG的頻率和電壓控制Fig.2 Frequency and voltage control in VSG

由圖2可知，在逆變器控制策略中加入同步發電機的特性，可提高微電網輸出頻率和電壓的穩定性。

2 轉動慣量和阻尼系數對VSG的影響

VSG技術不僅具有調頻、調壓特性，還能克服電力電子設備帶來的缺陷，使微電網具備轉動慣性和阻尼。然而，VSG的外特性受轉動慣量J和阻尼系數D這兩個關鍵參數的影響較大，為了獲得更好的運行性能，須對上述兩個關鍵參數進行詳細分析。

2.1 關鍵參數對輸出功率的影響

根據圖2可得VSG有功環的控制框圖，如圖3所示。

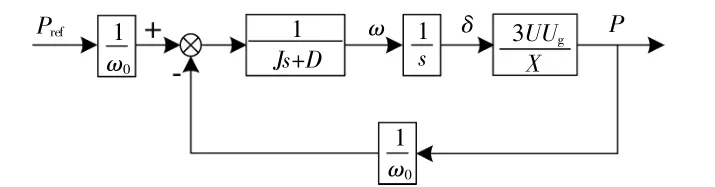
圖3 有功環控制框圖Fig.3 Control block diagram of active power loop

圖中：Pref為參考有功功率；P為VSG輸出有功功率；U為VSG輸出電壓；Ug為電網電壓；X為系統等效阻抗。

由圖3可得VSG有功環的閉環傳遞函數為

根據式（4）可得VSG輸出有功功率的單位階躍響應曲線，如圖4所示。

圖4 有功功率階躍響應曲線Fig.4 Step response curve of active power

由圖4可知，當J增大時，有功功率的超調量增大，動態響應慢，功率變化速度相對平緩，調節時間相應變長，功率出現振蕩現象，系統的穩定性受到一定的影響。當D變大時，系統阻尼增加，功率的超調量逐漸減小，動態響應慢，上升時間增大，功率波動逐漸減小，穩定性得以提高。

2.2 關鍵參數對輸出頻率的影響

根據圖3可得參考有功功率Pref與輸出頻率ω之間的傳遞函數為

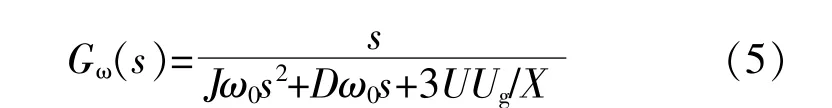
根據式（5）可得VSG輸出頻率的階躍響應曲線，如圖5所示。

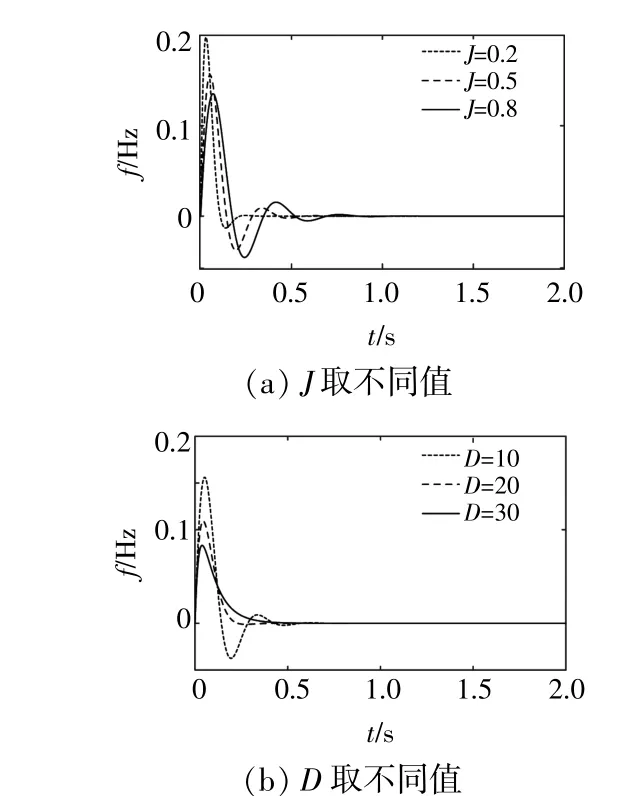
圖5 頻率階躍響應曲線Fig.5 Step response curve of frequency

由圖5可知，當J增大時，VSG的輸出頻率變化較為平緩，響應速度變慢，可有效抑制頻率突變，但同時也帶來頻率的振蕩。當D變大時，頻率的超調量減小，動態響應時間變長，可見D的增大能夠有效減小頻率的波動。

VSG有功環的動態性能由J和D這兩個關鍵參數共同決定，且對輸出功率和輸出頻率的影響又相互制約[11]。增大J可使頻率變化較為平緩，但增大了功率的超調量，并且加劇了系統的振蕩。減小J雖能夠減弱功率的振蕩，實現功率的快速響應，但會造成頻率的突變，帶來過大的超調。較大的D能夠減小功率及頻率的振蕩，使之變得平緩，但削弱了系統的動態響應速度。因此，針對系統特性之間的矛盾，應綜合考慮各項性能指標，折中選取J和D。

3 參數自適應控制策略

3.1 擾動狀態下的功角特性

VSG功角特性曲線如圖6所示。

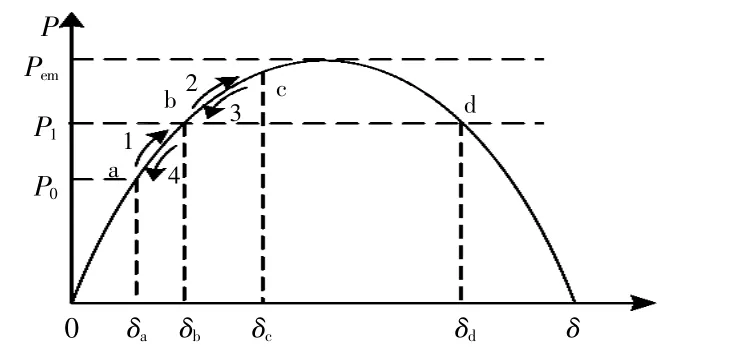
圖6 VSG功角特性曲線Fig.6 Power-Angle characteristic curve of VSG

當功率參考值從P0階躍到P1時，系統的穩態工作點從a點變化到b點。這一變化過程并不是瞬間完成的，而是存在一個逐漸衰減的振蕩過程。圖7為VSG暫態振蕩曲線。

圖7 VSG暫態振蕩曲線Fig.7 Transient oscillation curve of VSG

當系統處于第1階段（0～t1）時，VSG的給定功率大于輸出功率，促使角頻率加速增長，即dω/dt>0，且此時角頻率始終大于額定值。為防止頻率出現較大的超調而過多偏離額定值，應增大慣量J和阻尼D的取值，以減緩角頻率的變化率及其偏移量。

當系統處于第2階段（t1～t2）時，VSG的輸出功率大于給定值，角頻率到達峰值后開始向額定頻率回調，該階段的角頻率仍大于額定值，但變化率始終小于0，即dω/dt<0，角頻率處于減速階段。此過程應減小慣量J以減緩功率的超調，同時可以加速角頻率的回調，使其盡快回到額定值。同時在角頻率偏移較大時稍微增大阻尼D，以達到進一步減小頻率偏移的效果。

階段3和階段4的過程類似于階段1和階段2。由此可以根據角頻率的偏差量及其變化率來分別確定慣量J和阻尼D的選取原則，如表1所示。

表1 慣量J和阻尼D的選取原則Table 1 Principles of selecting inertia J and damping D

3.2 基于模糊控制的參數自適應算法

根據表1中慣量J和阻尼D的選取原則，利用模糊控制實現上述兩個參數的自適應變化，使系統具有較強的魯棒性和自適應性。

假設VSG輸出頻率為ω，偏差e=ω-ω0，偏差的變化率ec=de/dt。將連續域的e和ec轉換成離散域N=[-n，-n+1，…，-1，0，1，…，n-1，n]，n為離散量的檔數，本文取n=6。設在連續域內輸入量的取值范圍為[xL，xH]，則轉換到離散域的量化因子可以表示為

式中：x為連續域的e或ec；X為離散論域E或Ec。

將得到的模糊語言變量進行區間劃分，分別記為：{PL，PS，ZE，NS，NL}。其中，PL和PS分別代表偏離正方向較大和較小的數值；ZE表示沒有偏差；NS，NL分別代表偏離負方向較小和較大的數值。考慮到頻率偏差量E過0時有較高的區分度，此處選擇三角形隸屬度函數，其他位置均選用較為平滑的高斯型隸屬度函數。

輸入值的隸屬度函數如圖8所示。根據表1中參數的選取原則，制定模糊控制規則，如表2，3所示。

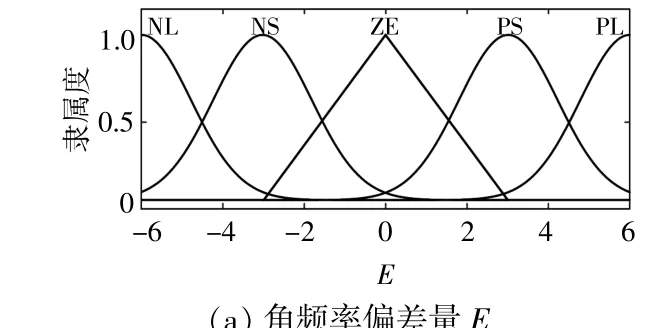
圖8 輸入量的隸屬度函數Fig.8 Membership function of the input

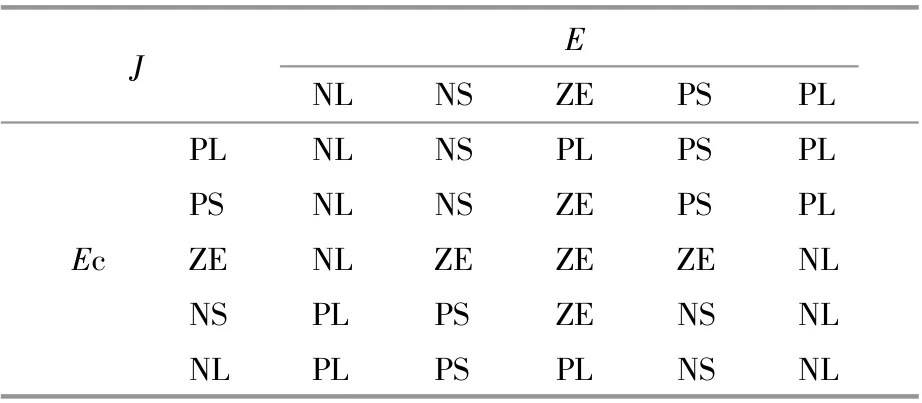
表2 慣量J的模糊控制規則表Table 2 Fuzzy control rule of inertia J

表3 阻尼D的模糊控制規則表Table 3 Fuzzy control rule of damping D

模糊控制下J的輸出呈現雙向發展，變化靈活，可設置大的初始慣量來抑制頻率的波動；D的輸出變化較為平緩，避免了阻尼過大而造成的響應緩慢的問題。由此可得輸出量的模糊集合，輸出量選擇適用性強、計算簡單的三角形隸屬度函數，如圖9所示，利用重心法，對輸出模糊集合求取加權平均值，論域仍為[-6，6]，得到最終輸出量U。

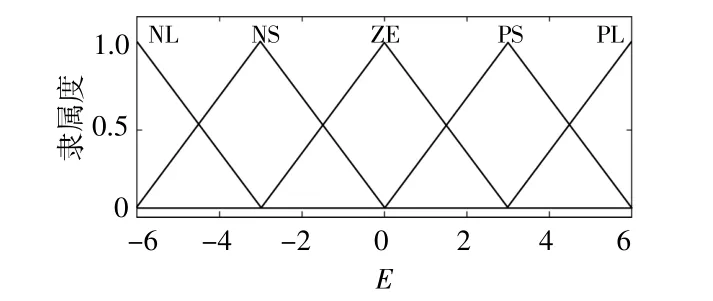
圖9 輸出量的隸屬度函數Fig.9 Membership function of the output

設自適應參數的調節范圍為[yL，yH]，將最終的模糊輸出量U轉換到連續域下的量化系數為

自適應參數y的輸出表達式為

式中：y為慣量J或阻尼D的自適應變化取值。

根據前文分析，可得基于模糊控制的慣量J和阻尼D的自適應控制框圖，如圖10所示。

圖10 基于模糊控制的自適應控制框圖Fig.10 Adaptive control diagram based on fuzzy control

4 仿真與實驗驗證

4.1 仿真驗證

為驗證基于模糊控制的參數自適應算法的可行性，在Simulink中搭建VSG模型進行仿真分析，仿真參數如表4所示。

表4 仿真參數Table 4 Simulation parameters

仿真工況為VSG并網運行，啟動時有功參考值為5 kW，2 s突增到10 kW，4.5 s再降為5 kW。對固定參數控制和參數自適應控制兩種方式進行對比仿真，結果如圖11，12所示。

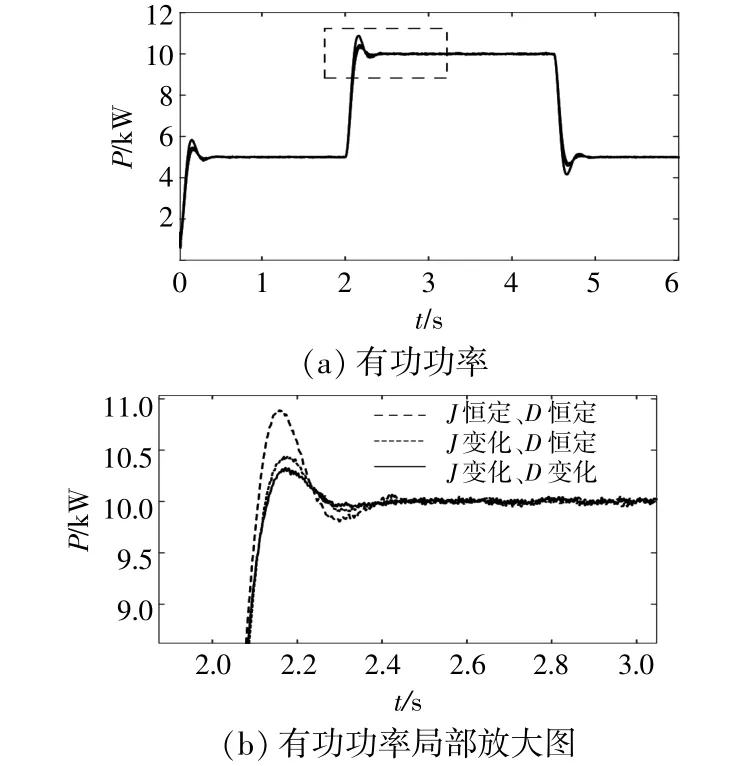
圖11 不同控制方式下的有功功率波形Fig.11 Active power waveforms under different controls

圖12 不同控制方式下的頻率波形Fig.12 Frequency waveforms under different controls

由圖11，12可得，參數固定不變時，有功和頻率均具有較大的超調，調節時間較長，系統有較大波動；僅采用慣量J自適應控制時，系統超調量降低，調節時間變短，系統波動得到抑制；采用慣量J和阻尼D雙參數自適應控制時，控制效果得到了進一步提高，驗證了基于模糊控制的參數自適應控制策略的有效性。

圖13為模糊控制自適應參數J和D的變化情況。

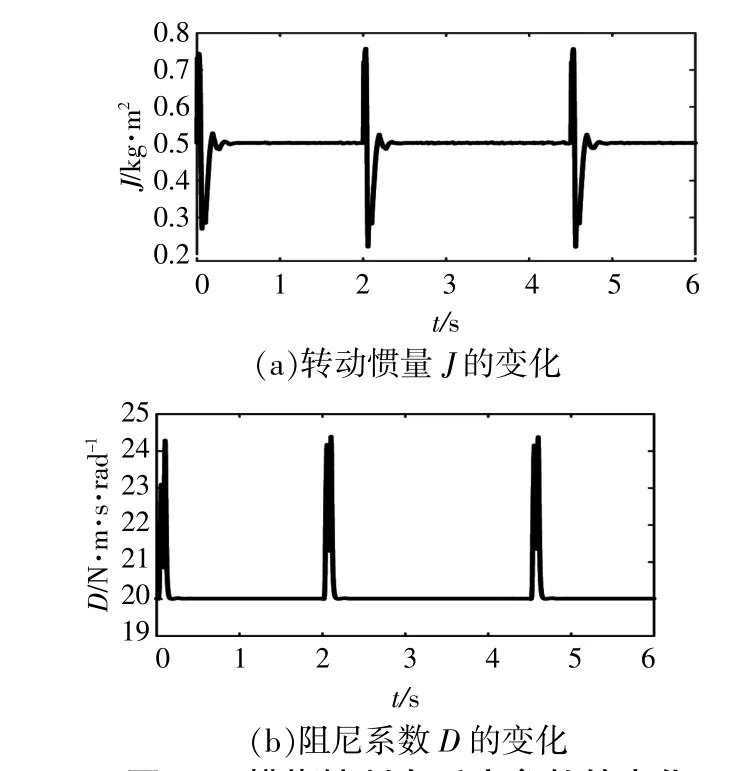
圖13 模糊控制自適應參數的變化Fig.13 Variation of adaptive parameters when fuzzy control is used

由圖13可以看出，參數J和D均連續變化，J以初始值為中心呈雙向變化，D的變化范圍相對較小，以免阻尼過大而減緩響應。系統發生振蕩時，J和D均增大，從而減小波動帶來的影響；頻率恢復時，J和D均減小以加快該過程。

4.2 實驗驗證

在基于TMS320F28335的LC型并網逆變器平臺上對參數自適應控制進行實驗驗證。t0時刻有功功率參考值增加1.5 kW，t1時刻減少0.75 kW，實驗結果如圖14所示。

圖14 不同控制方式下的有功功率波形Fig.14 Active power waveforms under different controls

由圖14可以看出，采用慣量J的自適應控制要比固定參數控制的功率變化更為平緩，而采用慣量J和阻尼D雙參數自適應控制的動態性能又優于前兩種控制方式，其超調更小，調節時間更短，有效抑制了有功功率波動。

5 結論

針對傳統虛擬同步發電機固定參數無法兼顧快速性和穩定性的特點，本文建立其數學模型，分析了轉動慣量和阻尼系數對虛擬同步發電機特性的影響。從功角特性出發，確定轉動慣量和阻尼系數的選取原則，進而提出一種基于模糊控制的虛擬同步發電機參數自適應控制策略，兼顧了系統動態調節的快速性和穩定性，同時增強了系統的魯棒性。通過與傳統固定參數控制策略的對比仿真和實驗，驗證了所提控制策略的可行性和有效性。