地鐵進(jìn)站客流量 SARIMA 與 GA-BP神經(jīng)網(wǎng)絡(luò)組合預(yù)測(cè)模型

強(qiáng)添綱，劉 濤，裴玉龍

（東北林業(yè)大學(xué) 交通學(xué)院，黑龍江 哈爾濱 150040）

0 引言

隨著城市經(jīng)濟(jì)的不斷發(fā)展，越來(lái)越多的城市選擇建設(shè)地鐵來(lái)緩解當(dāng)?shù)氐慕煌〒矶隆３鞘械罔F網(wǎng)絡(luò)規(guī)模不斷擴(kuò)大、客流量不斷增加等因素對(duì)地鐵的運(yùn)營(yíng)管理提出更高的要求，如何利用地鐵客流數(shù)據(jù)準(zhǔn)確預(yù)測(cè)未來(lái)一段時(shí)期的客流量，對(duì)于制定合理的運(yùn)營(yíng)管理策略尤為重要。

目前，客流量預(yù)測(cè)方法主要分為基于時(shí)間序列的統(tǒng)計(jì)預(yù)測(cè)模型、基于非參數(shù)的預(yù)測(cè)模型和組合預(yù)測(cè)模型。基于時(shí)間序列的預(yù)測(cè)模型方面，趙鵬等[1]利用季節(jié)求和自回歸移動(dòng)平均模型（SARIMA）對(duì)北京地鐵的端點(diǎn)站、中間站、換乘站及接駁站進(jìn)行客流預(yù)測(cè)，結(jié)果表明SARIMA模型有較高的預(yù)測(cè)精度。李潔等[2]利用SARIMA模型預(yù)測(cè)廣州南站、小欖站的發(fā)送客流量，與隨機(jī)森林（RF）、支持向量機(jī)（SVM）等預(yù)測(cè)方法對(duì)比發(fā)現(xiàn)在預(yù)測(cè)步長(zhǎng)較大時(shí)SARIMA模型最優(yōu)。馬超群等[3]利用求和自回歸移動(dòng)平均模型（ARIMA）進(jìn)行擬合，并與自回歸模型（AR）、支持向量線性回歸模型（SVR）、反向傳播（BP）神經(jīng)網(wǎng)絡(luò)進(jìn)行對(duì)比，發(fā)現(xiàn)在不同時(shí)間粒度下ARIMA模型平均預(yù)測(cè)精度最高。王瑩等[4]利用SARIMA模型對(duì)北京地鐵進(jìn)站客流量進(jìn)行預(yù)測(cè)，結(jié)果顯示模型預(yù)測(cè)的平均誤差為0.3%。

基于非參數(shù)預(yù)測(cè)模型方面，Du等[5]提出一種比傳統(tǒng)客流預(yù)測(cè)模型效果更好的深度不規(guī)則卷積殘差（DST-ICRL）長(zhǎng)短記憶（LSTM）網(wǎng)絡(luò)模型。Liu等[6]提出了一種端到端的深度學(xué)習(xí)架構(gòu)（DeepPF）來(lái)預(yù)測(cè)地鐵客流量，研究結(jié)果表明DeepPF擁有較高的預(yù)測(cè)精度。Li等[7]提出一種多尺度徑向基函數(shù)（MSRBF）網(wǎng)絡(luò)預(yù)測(cè)地鐵客流量，實(shí)驗(yàn)表明該模型預(yù)測(cè)精度高于其他智能模型。李潔等[8]根據(jù)時(shí)間序列數(shù)據(jù)建立循環(huán)神經(jīng)網(wǎng)絡(luò)（RNN）預(yù)測(cè)模型，結(jié)果表明RNN模型的預(yù)測(cè)精度與訓(xùn)練數(shù)據(jù)的類型和數(shù)量存在較大關(guān)系。谷金晶等[9]利用公交IC卡上車數(shù)據(jù)構(gòu)建BP神經(jīng)網(wǎng)絡(luò)和徑向基函數(shù)（RBF）神經(jīng)網(wǎng)絡(luò)，試驗(yàn)結(jié)果表明RBF神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)效果更好。

組合預(yù)測(cè)模型方面，Wei等[10]提出了一種將經(jīng)驗(yàn)?zāi)Ｊ椒纸猓‥MD）和BP神經(jīng)網(wǎng)絡(luò)相結(jié)合的混合EMD-BPN方法用于地鐵客流量預(yù)測(cè)。Dimitriou等[11]提出一種基于自適應(yīng)混合模糊規(guī)則系統(tǒng)（FRBS）的城市干道交通流短期預(yù)測(cè)方法，試驗(yàn)結(jié)果表明該方法優(yōu)于傳統(tǒng)的遺傳算法。Zheng等[12]基于BP神經(jīng)網(wǎng)絡(luò)、RBF神經(jīng)網(wǎng)絡(luò)和貝葉斯定理構(gòu)建貝葉斯組合預(yù)測(cè)模型，結(jié)果表明該模型預(yù)測(cè)結(jié)果較好但魯棒性較差。Hong等[13]提出一種基于SVR模型和連續(xù)蟻群優(yōu)化算法（SVRCACO）的城市間交通流短期預(yù)測(cè)模型，結(jié)果表明該模型預(yù)測(cè)結(jié)果優(yōu)于SARIMA模型。趙建立等[14]提出一種基于卷積神經(jīng)網(wǎng)絡(luò)（CNN）與殘差網(wǎng)絡(luò)（ResNet）的組合預(yù)測(cè)模型（ResNet-CNN1D），結(jié)果表明該模型預(yù)測(cè)精度更高。林浩等[15]基于遺傳算法（GA）和粒子群算法（PSO）構(gòu)建GAPSO-SVM模型，實(shí)驗(yàn)顯示GAPSO- SVM模型有較高的預(yù)測(cè)精度。黃益紹等[16]基于粗糙集（RS）和改進(jìn)粒子群（IPSO）構(gòu)建優(yōu)化支持向量機(jī)（RS-IPSOSVM）的公交客流預(yù)測(cè)方法，結(jié)果表明該方法簡(jiǎn)化了訓(xùn)練樣本，解決了SVM參數(shù)選擇的盲目性。

地鐵進(jìn)站客流是具有一定周期性的時(shí)間序列數(shù)據(jù)，考慮SARIMA模型預(yù)測(cè)效果較好且所需數(shù)據(jù)較少，傳統(tǒng)研究一般使用該模型對(duì)客流進(jìn)行預(yù)測(cè)；而隨著計(jì)算機(jī)技術(shù)的迅猛發(fā)展，且為解決SARIMA模型無(wú)法考慮相關(guān)因素對(duì)進(jìn)站客流量影響的缺點(diǎn)，越來(lái)越多學(xué)者選擇使用神經(jīng)網(wǎng)絡(luò)等算法預(yù)測(cè)客流量。考慮神經(jīng)網(wǎng)絡(luò)等算法容易出現(xiàn)局部極小化等問(wèn)題，在已有研究基礎(chǔ)上提出一種基于SARIMA模型和GA-BP神經(jīng)網(wǎng)絡(luò)的地鐵進(jìn)站客流組合預(yù)測(cè)模型。研究先分別對(duì)SARIMA模型和GA-BP神經(jīng)網(wǎng)絡(luò)參數(shù)進(jìn)行標(biāo)定，在獲取到SARIMA模型和GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)值的基礎(chǔ)上，結(jié)合SARIMA模型的最大季節(jié)回歸多項(xiàng)式個(gè)數(shù)明確組合模型因變量個(gè)數(shù)來(lái)確定組合模型的權(quán)重值，并最終建立線性組合預(yù)測(cè)模型。

1 線性組合預(yù)測(cè)模型建立

1.1 季節(jié)求和自回歸移動(dòng)平均模型

考慮季節(jié)求和自回歸移動(dòng)平均（SARIMA）模型能夠很好地描述客流量數(shù)據(jù)的趨勢(shì)變化和季節(jié)周期特性，且城市地鐵進(jìn)站客流量屬于周期性的時(shí)間序列數(shù)據(jù)，因而選擇該模型作為子模型對(duì)進(jìn)站客流預(yù)測(cè)。SARIMA模型是在自回歸移動(dòng)平均模型的基礎(chǔ)上考慮到時(shí)間序列周期變化的季節(jié)性所帶來(lái)不平穩(wěn)現(xiàn)象做出改進(jìn)，通過(guò)對(duì)含有季節(jié)性周期的時(shí)間序列進(jìn)行季節(jié)差分的方法將其化為平穩(wěn)序列。SARIMA（p，d，q） （P，D，Q）S計(jì)算公式為

式中：Φ1，Φ2，…，ΦP為季節(jié)自回歸系數(shù)；φ1，φ2，…，φp為非季節(jié)自回歸系數(shù)；Θ1，Θ2，…，ΘQ為季節(jié)移動(dòng)平均系數(shù)；θ1，θ2，…，θq為非季節(jié)移動(dòng)平均系數(shù)；αt為t時(shí)刻的白噪聲；?SD為D階季節(jié)周期為S的差分算子；?d為d階差分算子；xt為過(guò)去各期誤差αt，αt-1，…，α1的線性組合；B為滯后算子。

其中，上述公式所對(duì)應(yīng)的ΦP（BS）為P階季節(jié)自回歸系數(shù)多項(xiàng)式；Φp（B）為p階自回歸多項(xiàng)式；ΘQ（BS）為Q階季節(jié)移動(dòng)平均多項(xiàng)式；Θq為q階移動(dòng)平均多項(xiàng)式；為平穩(wěn)的時(shí)間序列。

1.2 GA-BP神經(jīng)網(wǎng)絡(luò)模型

傳統(tǒng)SARIMA模型無(wú)法考慮地鐵發(fā)車次數(shù)等因素對(duì)進(jìn)站客流的影響，為研究不同因素對(duì)客流的影響，研究選擇使用GA-BP神經(jīng)網(wǎng)絡(luò)作為子模型對(duì)地鐵客流進(jìn)行預(yù)測(cè)。BP神經(jīng)網(wǎng)絡(luò)是一種利用梯度下降法使其實(shí)際輸出值和期望輸出值誤差均方差為最小的多層前饋神經(jīng)網(wǎng)絡(luò)，正因如此BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)時(shí)容易陷入局部最小值。研究選擇使用遺傳算法（GA）獲取BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)重值和閾值，降低BP算法陷入局部最小值可能性[17-18]， GA-BP算法流程如圖1所示。

圖1 GA-BP算法流程圖Fig.1 Flow chart of GA-BP algorithm

模型以累計(jì)誤差最小為目標(biāo)，計(jì)算公式為

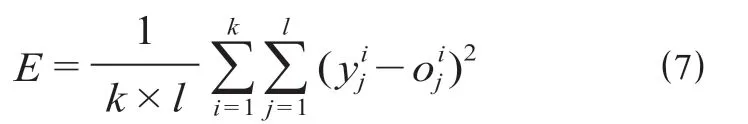
式中：E為累計(jì)誤差；為BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)第i個(gè)樣本下第j維變量的預(yù)測(cè)值；為第i個(gè)樣本下第j維變量對(duì)應(yīng)的實(shí)際值；l為輸出變量的維數(shù)；k為訓(xùn)練樣本個(gè)數(shù)。

GA-BP神經(jīng)網(wǎng)絡(luò)訓(xùn)練步驟如下。

（1）步驟1：確定網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)。確定網(wǎng)絡(luò)輸入層節(jié)點(diǎn)數(shù)a，隱含層節(jié)點(diǎn)數(shù)b，輸出層節(jié)點(diǎn)數(shù)c，輸入層與隱含層神經(jīng)元之間的連接權(quán)值，隱含層與輸出層連接權(quán)值，隱含層閾值，輸出層閾值

（2）步驟2：隨機(jī)化初始種群。個(gè)體采用實(shí)數(shù)編碼方式，由輸入層與隱含層連接權(quán)值、隱含層閾值、隱含層與輸出層連接權(quán)值以及輸出層閾值4部分組成，具體構(gòu)成如公式（8）所示。

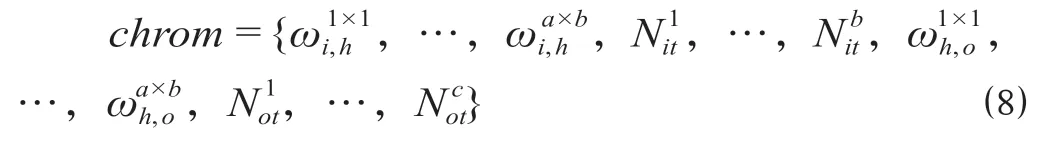
（3）步驟3：確定適應(yīng)度函數(shù)。利用BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)結(jié)果與實(shí)際結(jié)果之間誤差的絕對(duì)值之和作為個(gè)體適應(yīng)度值f，其計(jì)算公式為

式中：yi為輸出層第i個(gè)節(jié)點(diǎn)的預(yù)測(cè)值；oi為輸出層第i個(gè)節(jié)點(diǎn)的實(shí)際值。

（4）步驟4：選擇操作。研究選擇輪盤(pán)賭法，通過(guò)適應(yīng)度比例確定個(gè)體i的選擇概率pi，計(jì)算公式為

式中：Fi為個(gè)體i修正后的適應(yīng)度值；fi為個(gè)體i的適應(yīng)度值；k1為系數(shù)；n為種群個(gè)體數(shù)目。

（5）步驟5：交叉操作。研究選擇實(shí)數(shù)交叉法，即第m個(gè)染色體gme和第l個(gè)染色體gle在e位交叉，交叉的計(jì)算公式為

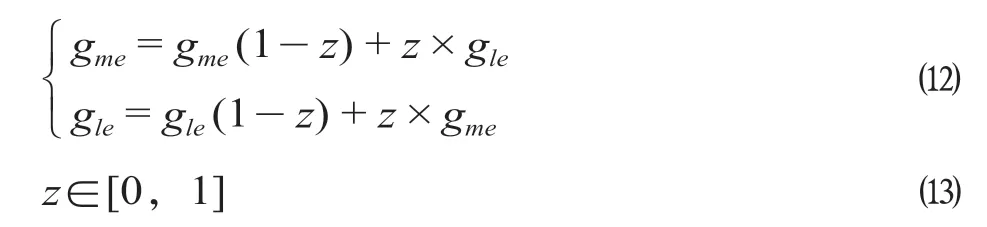
式中：z為[0，1]區(qū)間的隨機(jī)值。

（6）步驟6：變異操作。選取第i個(gè)個(gè)體的第e個(gè)基因gie進(jìn)行變異，考慮基因變異是一種隨機(jī)現(xiàn)象，采用一個(gè)在[0，1]區(qū)間的隨機(jī)值r來(lái)決定該基因的變異方式，具體變異方式如下。

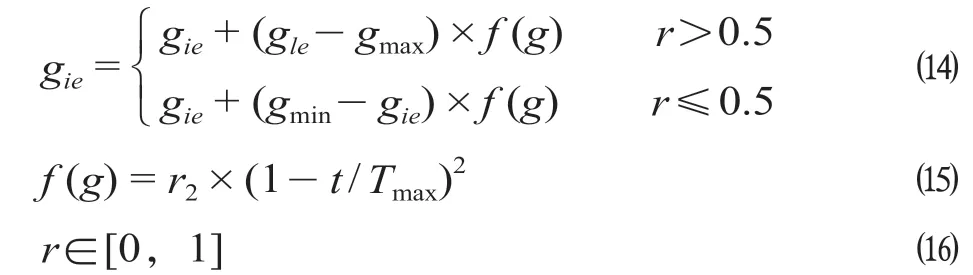
式中：gmax為基因gie的上界；gmin為基因gie的下界；r2為一個(gè)隨機(jī)數(shù)；t為當(dāng)前迭代次數(shù)；Tmax為最大迭代次數(shù)。

（7）步驟7：計(jì)算適應(yīng)度函數(shù)值。如果滿足算法結(jié)束條件則輸出優(yōu)化的權(quán)值和閾值，反之則返回步驟4。

（8）步驟8：隱含層計(jì)算。隱含層激勵(lì)函數(shù)選擇tansig函數(shù)，計(jì)算公式為

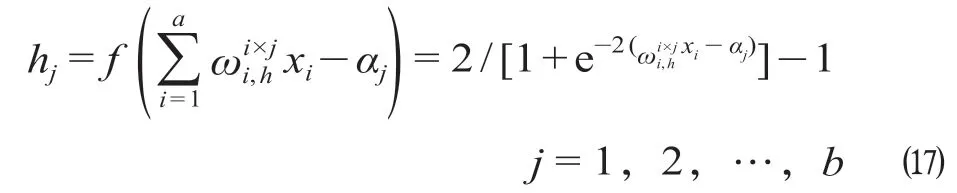
式中：xi為第i個(gè)個(gè)體輸入值；αj為第j個(gè)系數(shù)。

（9）步驟9：輸出層計(jì)算。

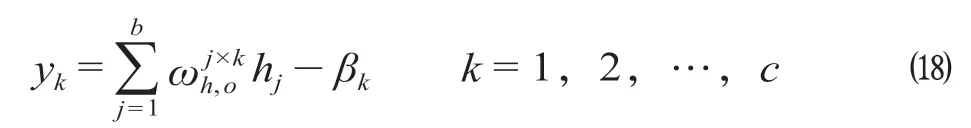
式中：βk為第k個(gè)系數(shù)。

（10）步驟10：判斷是否滿足結(jié)束條件，若不滿足結(jié)束條件則返回步驟8。

1.3 組合預(yù)測(cè)模型

盡管利用遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值，但該模型依然存在陷入局部最小值問(wèn)題。為解決這一問(wèn)題并提高模型的預(yù)測(cè)精度，研究在SARIMA模型和GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)值的基礎(chǔ)上進(jìn)一步地修正預(yù)測(cè)值。研究考慮時(shí)間序列季節(jié)性波動(dòng)的特性，結(jié)合SARIMA模型的季節(jié)周期S、季節(jié)自回歸系數(shù)多項(xiàng)式對(duì)應(yīng)階數(shù)P和季節(jié)移動(dòng)平均多項(xiàng)式對(duì)應(yīng)階數(shù)Q選取某一歷史時(shí)間段內(nèi)的多個(gè)子模型預(yù)測(cè)結(jié)果，并根據(jù)其預(yù)測(cè)精度確定組合預(yù)測(cè)模型對(duì)應(yīng)的權(quán)重值。

考慮SARIMA模型可以確定該時(shí)間序列數(shù)據(jù)是以S個(gè)步長(zhǎng)為一個(gè)季節(jié)周期，其組合預(yù)測(cè)模型構(gòu)建的具體思路如下。

（1）先明確需要預(yù)測(cè)數(shù)據(jù)在一個(gè)季節(jié)周期內(nèi)的具體位置（如一個(gè)星期內(nèi)的第4位則是星期四），以該位置為原點(diǎn)統(tǒng)計(jì)出訓(xùn)練集最近v個(gè)季節(jié)周期內(nèi)相同位置2個(gè)模型的預(yù)測(cè)值，并計(jì)算其對(duì)應(yīng)的平均絕對(duì)百分比誤差（MAPE），具體計(jì)算公式為

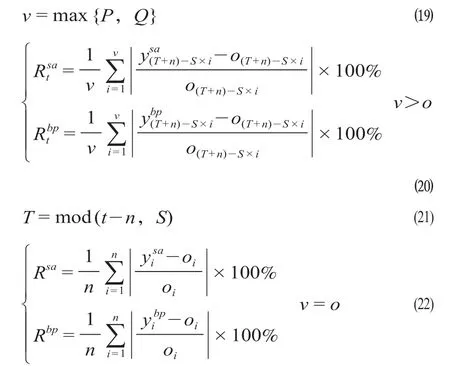
式中：Rtsa為SARIMA模型預(yù)測(cè)第t個(gè)數(shù)據(jù)的MAPE；Rtbp為GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)第t個(gè)數(shù)據(jù)的MAPE；Rsa為SARIMA模型在訓(xùn)練集下的MAPE；Rbp為GA-BP神經(jīng)網(wǎng)絡(luò)在訓(xùn)練集下的MAPE；為 SARIMA模型預(yù)測(cè)步長(zhǎng)為（T+n） -S×i時(shí)的預(yù)測(cè)值；為GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)步長(zhǎng)為（T+n） -S×i時(shí)的預(yù)測(cè)值；o（T+n）-S×i為第（T+n） -S×i個(gè)數(shù)據(jù)的實(shí)際值；t為所需要預(yù)測(cè)數(shù)據(jù)值的序號(hào)；n為訓(xùn)練集的個(gè)數(shù)；S為季節(jié)周期長(zhǎng)度；T為（t-n）與S的余數(shù)。

（2）為避免MAPE值過(guò)小，并讓更小的MAPE模型擁有更大的權(quán)重。將子模型MAPE值轉(zhuǎn)變?yōu)榈箶?shù)，再進(jìn)行歸一化處理后作為組合預(yù)測(cè)模型的權(quán)重值，計(jì)算公式為

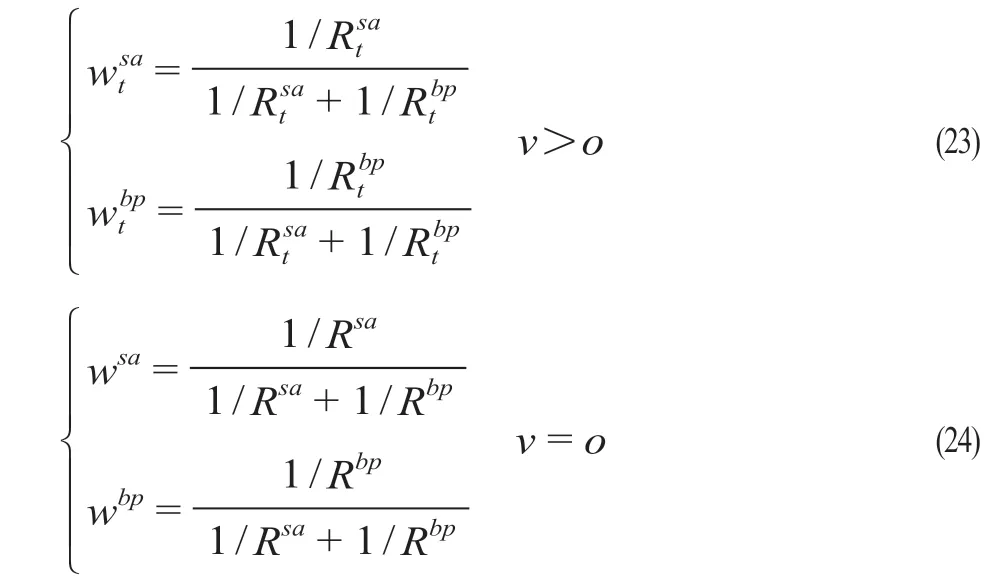
式中：wtsa為使用SARIMA模型預(yù)測(cè)第t個(gè)數(shù)據(jù)所對(duì)應(yīng)歸一化值；wtbp為使用GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)第t個(gè)數(shù)據(jù)所對(duì)應(yīng)歸一化值；wsa為當(dāng)v= 0時(shí)使用SARIMA模型預(yù)測(cè)第t個(gè)數(shù)據(jù)所對(duì)應(yīng)歸一化值；wbp為當(dāng)v= 0時(shí)使用GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)第t個(gè)數(shù)據(jù)所對(duì)應(yīng)歸一化值。

（3）結(jié)合權(quán)重值和子模型的預(yù)測(cè)值構(gòu)建線性組合模型，計(jì)算公式為

式中：ytpr為使用組合預(yù)測(cè)模型預(yù)測(cè)第t個(gè)時(shí)刻的預(yù)測(cè)值；ytsa為使用SARIMA模型預(yù)測(cè)第t個(gè)時(shí)刻的預(yù)測(cè)值；ytbp為使用GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)第t個(gè)時(shí)刻的預(yù)測(cè)值。

可以發(fā)現(xiàn)，研究構(gòu)建的組合模型考慮季節(jié)性因素，實(shí)質(zhì)上是對(duì)一個(gè)季節(jié)周期內(nèi)每一個(gè)時(shí)刻都構(gòu)建一個(gè)線性組合預(yù)測(cè)模型，權(quán)重均是以多個(gè)其他季節(jié)周期內(nèi)對(duì)應(yīng)時(shí)刻的百分誤差為依據(jù)計(jì)算。

2 實(shí)例分析

2.1 案例數(shù)據(jù)來(lái)源

研究利用2020年7月1日—2020年9月20日（共82 d）哈爾濱南站進(jìn)站客流數(shù)據(jù)標(biāo)定模型參數(shù)，使用2020年9月21日—2020年9月30日（共10 d）哈爾濱南站進(jìn)站客流量進(jìn)行預(yù)測(cè)。

2.2 SARIMA模型預(yù)測(cè)

通過(guò)對(duì)數(shù)據(jù)進(jìn)行1階7步差分消除長(zhǎng)期趨勢(shì)和季節(jié)性周期影響，再依據(jù)差分后的自相關(guān)-偏自相關(guān)分析圖反復(fù)嘗試建立SARIMA （2，1，2） （1，1，3）7模型，自相關(guān)－偏自相關(guān)分析圖如圖2所示。模型的擬合優(yōu)度R2值為0.79，SARIMA模型預(yù)測(cè)結(jié)果如表1所示。

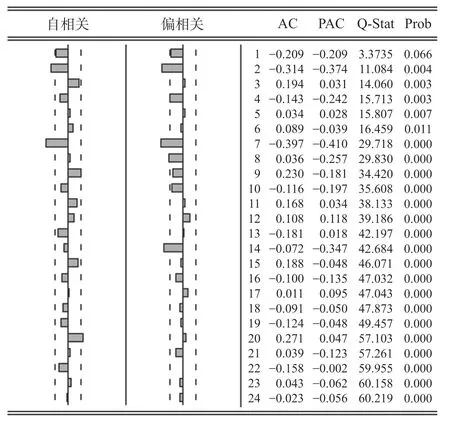
圖2 自相關(guān)-偏自相關(guān)分析圖Fig.2 Autocorrelation-partial autocorrelation analysis diagram

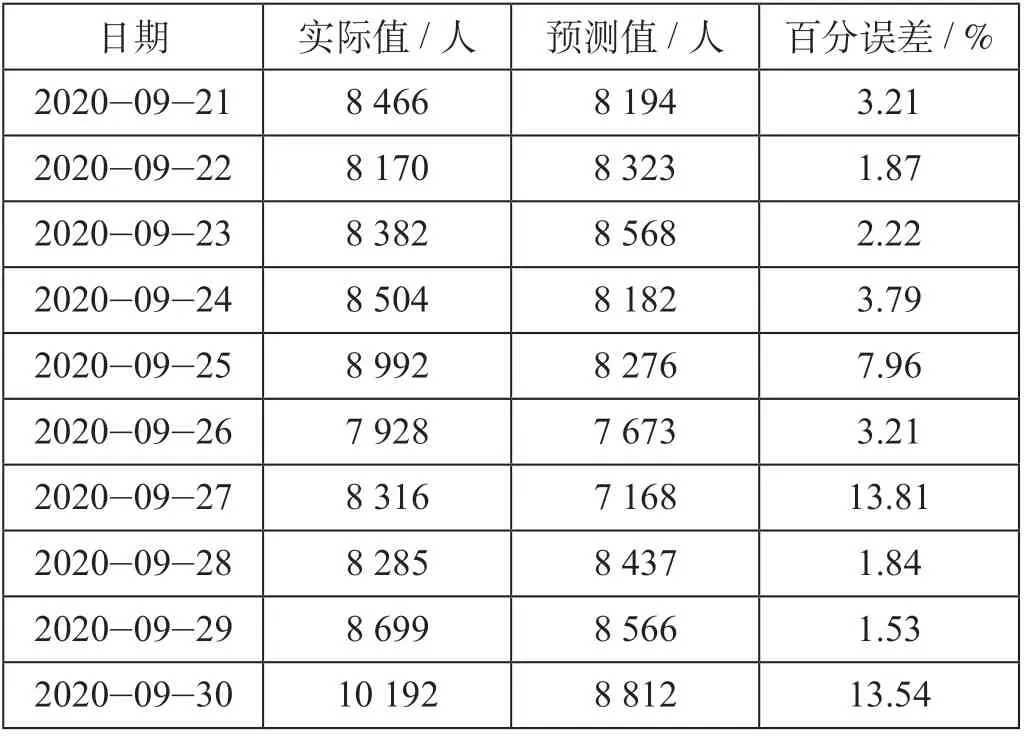
表1 SARIMA模型預(yù)測(cè)結(jié)果Tab.1 Prediction of SARIMA model

2.3 GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)

研究選取每日發(fā)車次數(shù)、是否工作日和周期數(shù)作為輸入變量，并對(duì)訓(xùn)練集的輸入變量和輸出變量進(jìn)行歸一化處理，消除量綱不統(tǒng)一對(duì)模型的影響。

遺傳算法的參數(shù)設(shè)定：總?cè)阂?guī)模為25，迭代500次，交叉概率為0.4，變異概率為0.2。

BP神經(jīng)網(wǎng)絡(luò)的參數(shù)設(shè)定：隱含層節(jié)點(diǎn)個(gè)數(shù)12個(gè)，訓(xùn)練次數(shù)為600次，學(xué)習(xí)速率為0.125，訓(xùn)練目標(biāo)為0.000 05。GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)結(jié)果如表2所示。研究參考文獻(xiàn)[19]使用校正后的擬合優(yōu)度作為評(píng)判標(biāo)準(zhǔn)，其校正擬合優(yōu)度R2值為0.65。

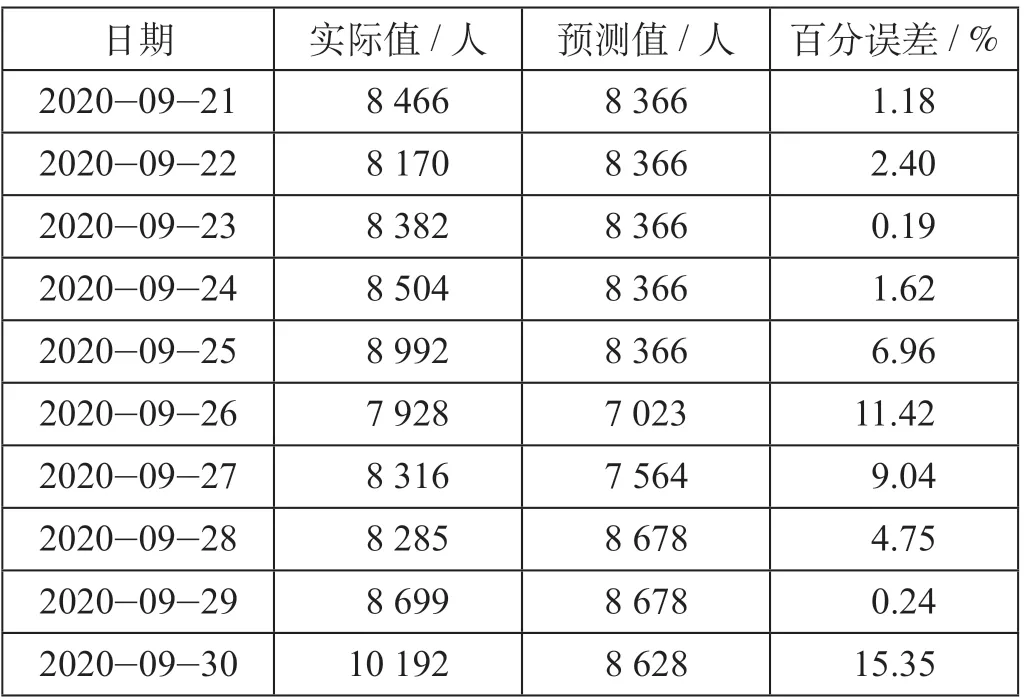
表2 GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)結(jié)果Tab.2 Prediction of GA-BP neural network

2.4 組合模型預(yù)測(cè)

首先利用擬合的SARIMA模型和GA-BP神經(jīng)網(wǎng)絡(luò)對(duì)訓(xùn)練集進(jìn)行預(yù)測(cè)，考慮到SARIMA模型預(yù)測(cè)需要基于歷史數(shù)據(jù)，因而只預(yù)測(cè)7月18日—9月20日共65 d的數(shù)據(jù)。接著計(jì)算2個(gè)子模型的MAPE，接著利用公式（19）—（24）計(jì)算8月31日—9月20日共21 d （v為3，S為7）每天的MAPE及其倒數(shù)。最后確定組合預(yù)測(cè)模型所對(duì)應(yīng)子模型的權(quán)重值，并得出組合模型的擬合優(yōu)度R2值為0.63，組合模型預(yù)測(cè)值如表3所示。

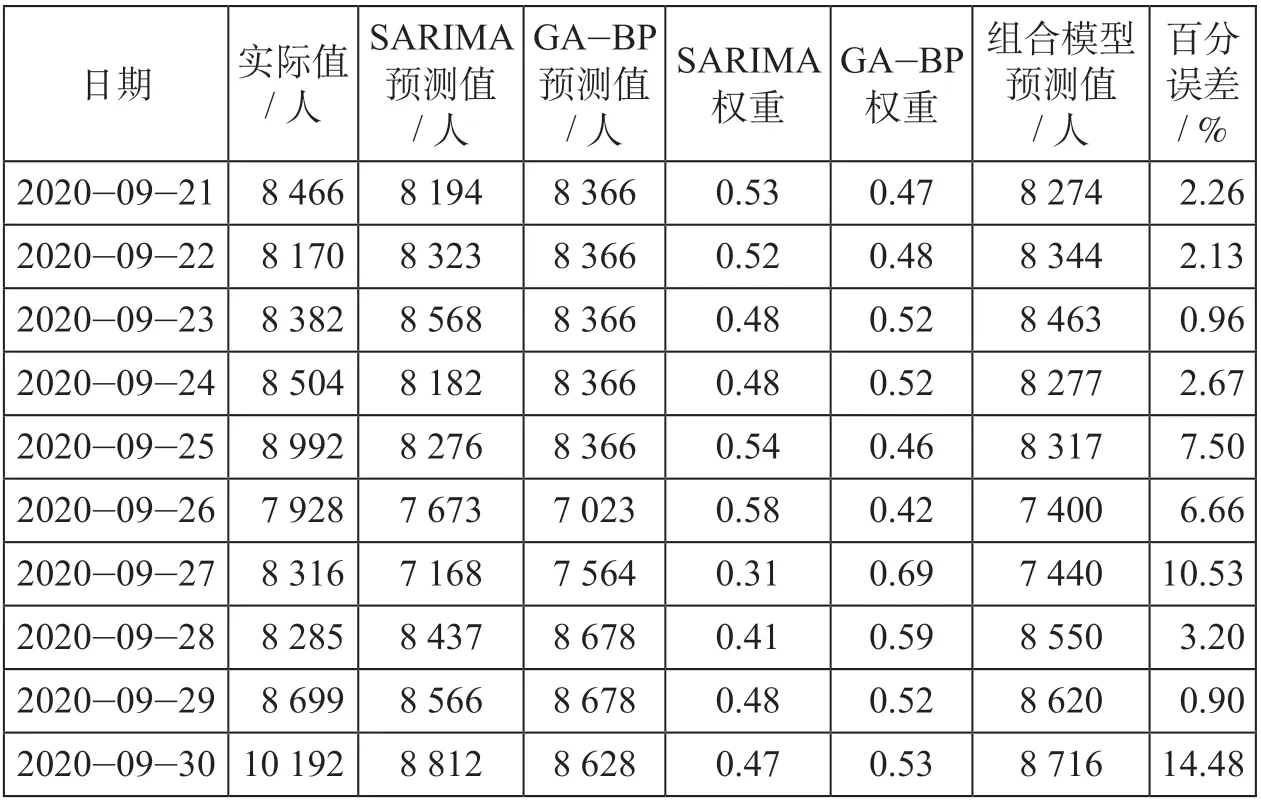
表3 組合模型預(yù)測(cè)值Tab.3 Predicted value of the combined model

參考文獻(xiàn)[19]，研究設(shè)定擬合優(yōu)度和校正擬合優(yōu)度值不低于0.60時(shí)通過(guò)擬合優(yōu)度檢驗(yàn)。就R2值而言，SARIMA模型、GA-BP神經(jīng)網(wǎng)絡(luò)、組合模型均通過(guò)擬合優(yōu)度檢驗(yàn)。事實(shí)上，R2值大小不僅與預(yù)測(cè)結(jié)果相關(guān)，還與樣本量的多少存在關(guān)系。本研究的訓(xùn)練樣本為82個(gè)，SARIMA模型預(yù)測(cè)的訓(xùn)練樣本為65個(gè)，GA-BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)的訓(xùn)練樣本為82個(gè)，組合模型預(yù)測(cè)的訓(xùn)練樣本為44個(gè)，這樣計(jì)算的R2值無(wú)法用于對(duì)比分析。為更好地對(duì)比分析各模型，選擇組合模型對(duì)應(yīng)的訓(xùn)練樣本和實(shí)際客流值重新計(jì)算R2值，得出SARIMA模型為0.80，GA-BP神經(jīng)網(wǎng)絡(luò)為0.44，組合模型為0.63。可以發(fā)現(xiàn)，SARIMA模型對(duì)于地鐵客流這類周期性的時(shí)間序列數(shù)據(jù)預(yù)測(cè)有著較為明顯的優(yōu)勢(shì)；GA-BP神經(jīng)網(wǎng)絡(luò)在樣本量較小時(shí)擬合優(yōu)度遠(yuǎn)低于樣本數(shù)為82個(gè)時(shí)的R2值，這表明模型的預(yù)測(cè)波動(dòng)性較大；組合模型的擬合優(yōu)度介于子模型間，能夠避免單一模型樣本量較少時(shí)擬合優(yōu)度過(guò)低問(wèn)題。

此外，為了更好地研究提出組合模型的效果，研究加入一個(gè)傳統(tǒng)的線性組合預(yù)測(cè)模型（以下簡(jiǎn)稱“組合模型0”）。該模型不同于組合模型根據(jù)一定規(guī)則挑選部分預(yù)測(cè)值的MAPE值作為其權(quán)重值的確定依據(jù)，組合模型0是以SARIMA模型和GA-BP神經(jīng)網(wǎng)絡(luò)所有預(yù)測(cè)值的百分誤差之和作為其權(quán)重值確定依據(jù)，其計(jì)算公式為

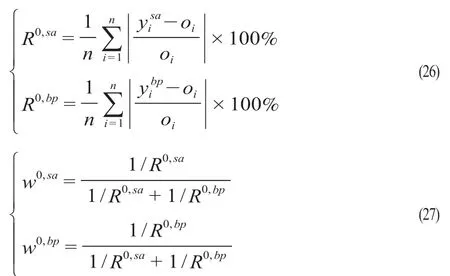
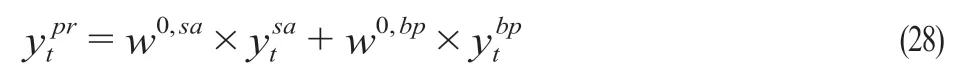
式中：R0,sa，R0,bp為SARIMA和GA-BP神經(jīng)網(wǎng)絡(luò)的MAPE值；w0,sa，w0,bp為組合模型0的SARIMA和GA-BP神經(jīng)網(wǎng)絡(luò)的權(quán)重值。

組合模型0的預(yù)測(cè)結(jié)果如表4所示。

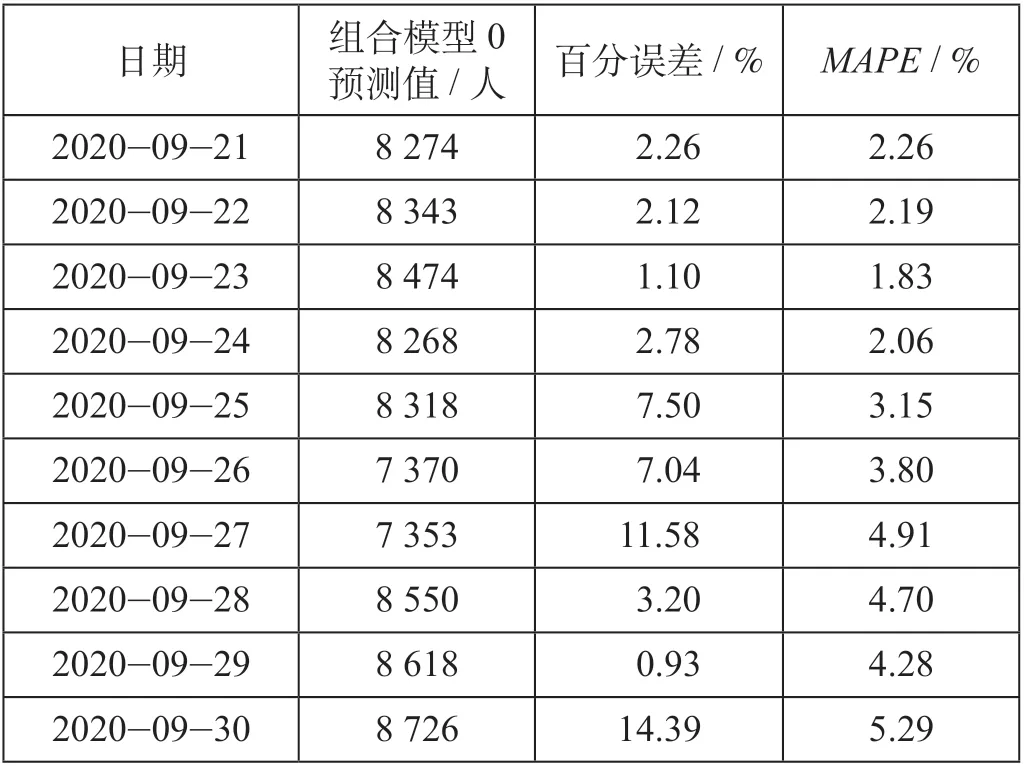
表 4 組合模型0的預(yù)測(cè)結(jié)果Tab.4 Prediction of combined model 0

2.5 模型結(jié)果分析

研究統(tǒng)計(jì)子模型與組合預(yù)測(cè)模型的百分誤差并計(jì)算得出預(yù)測(cè)不同個(gè)數(shù)下的MAPE，各模型的百分誤差和MAPE如表5所示，對(duì)應(yīng)的百分誤差和MAPE折線圖如圖3所示。

結(jié)合表5和圖3可以發(fā)現(xiàn)，子模型的百分誤差上下波動(dòng)較大，組合模型介于兩者之間，這表明組合模型有效緩解單一模型預(yù)測(cè)時(shí)出現(xiàn)波動(dòng)較大的可能性。其中，組合預(yù)測(cè)模型的百分誤差始終處于子模型之間，這表明組合預(yù)測(cè)模型的預(yù)測(cè)精度取決于子模型的預(yù)測(cè)精度，只有當(dāng)所有子模型預(yù)測(cè)精度達(dá)到同一水平時(shí)組合預(yù)測(cè)模型的預(yù)測(cè)精度相對(duì)較高，組合預(yù)測(cè)模型并不能在子模型的基礎(chǔ)上進(jìn)一步提升其預(yù)測(cè)精度。通過(guò)對(duì)比組合模型0的百分誤差可以發(fā)現(xiàn)，預(yù)測(cè)的10個(gè)數(shù)據(jù)中僅有2個(gè)預(yù)測(cè)值不如組合模型0，這表明研究提出的組合模型優(yōu)于組合模型0。

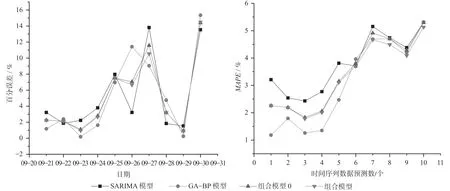
圖3 百分誤差和MAPE折線圖Fig.3 Line charts of percentage error and MAPE

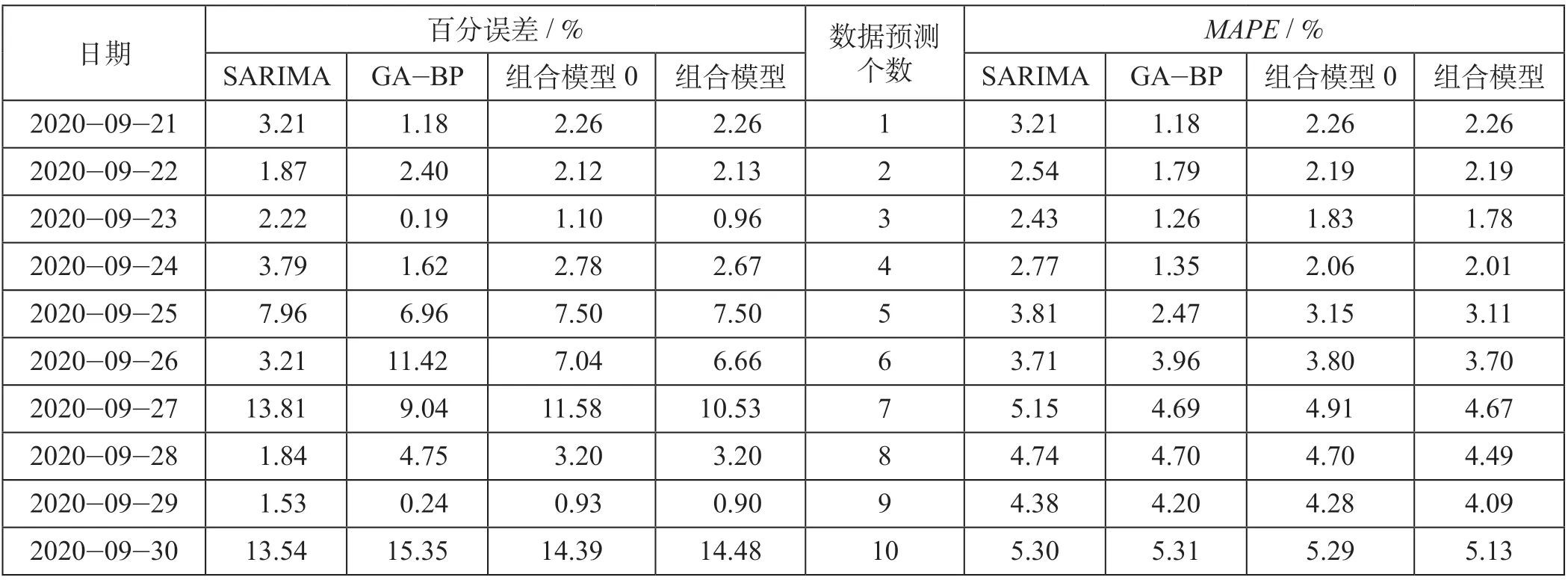
表5 各模型的百分誤差和MAPETab.5 Percentage error and MAPE of varied models

通過(guò)觀察各模型的MAPE、百分誤差可以發(fā)現(xiàn)，MAPE值隨著預(yù)測(cè)個(gè)數(shù)增加不斷提高，但各模型MAPE值均不高于10%，且組合模型隨著預(yù)測(cè)個(gè)數(shù)的增加，MAPE值增長(zhǎng)速率越低，這表明組合模型長(zhǎng)期預(yù)測(cè)效果較好。其中，SARIMA模型在短期預(yù)測(cè)（≤5 d）時(shí)預(yù)測(cè)精度較差，但是在長(zhǎng)期預(yù)測(cè)（＞5 d）時(shí)均高于GA-BP神經(jīng)網(wǎng)絡(luò)；GA-BP神經(jīng)網(wǎng)絡(luò)在短期預(yù)測(cè)時(shí)預(yù)測(cè)精度高于SARIMA模型，但在長(zhǎng)期預(yù)測(cè)時(shí)預(yù)測(cè)精度不如SARIMA模型；組合模型0無(wú)論在長(zhǎng)期還是短期預(yù)測(cè)中，預(yù)測(cè)精度大體介于子模型之間；組合預(yù)測(cè)模型在短期預(yù)測(cè)中受限于預(yù)測(cè)個(gè)數(shù)過(guò)少緣故，預(yù)測(cè)精度一直介于子模型之間，但在長(zhǎng)期預(yù)測(cè)時(shí)組合預(yù)測(cè)模型的預(yù)測(cè)精度好于所有子模型，當(dāng)預(yù)測(cè)個(gè)數(shù)大于2個(gè)時(shí)，組合模型的預(yù)測(cè)精度高于組合模型0。

3 結(jié)論

（1）研究從數(shù)據(jù)驅(qū)動(dòng)的角度提出一種利用SARIMA模型確定未來(lái)客流受某一或多個(gè)特定歷史客流影響的方法，同時(shí)構(gòu)建了考慮發(fā)車班次等因素的GA-BP神經(jīng)網(wǎng)絡(luò)模型對(duì)客流預(yù)測(cè)，并在此基礎(chǔ)上提出了一種既考慮歷史地鐵進(jìn)站客流對(duì)未來(lái)的影響又考慮發(fā)車班次、是否工作日等因素對(duì)客流影響的組合預(yù)測(cè)模型。

（2）在擬合優(yōu)度方面，研究提出的組合預(yù)測(cè)模型擬合優(yōu)度值雖然介于子模型之間，但是能夠避免單一模型在樣本量較少的情況下擬合優(yōu)度過(guò)低無(wú)法通過(guò)檢驗(yàn)的問(wèn)題，這表明研究提出的組合預(yù)測(cè)模型能夠較好地兼容不同的樣本量。

（3）在預(yù)測(cè)結(jié)果方面，研究提出的組合預(yù)測(cè)模型在短期預(yù)測(cè)中平均預(yù)測(cè)精度介于子模型之間，但在長(zhǎng)期預(yù)測(cè)過(guò)程中其平均預(yù)測(cè)精度優(yōu)于所有子模型，這表明研究提出的組合模型更適合用于長(zhǎng)期預(yù)測(cè)。此外，研究提出的組合模型預(yù)測(cè)精度高于組合模型0，這表明線性組合模型0并不適用于地鐵進(jìn)站客流預(yù)測(cè)。