基于區(qū)間分析的汽車起重機(jī)結(jié)構(gòu)非概率可靠性研究*

莫光輝 王 濤 田國富

沈陽工業(yè)大學(xué)機(jī)械工程學(xué)院 沈陽 110870

0 引言

汽車起重機(jī)是現(xiàn)代工業(yè)中不可缺少的設(shè)備，它在很大程度上減輕了勞動強(qiáng)度，其安全問題隨之受到高度重視。臂架作為汽車起重機(jī)的主要承載結(jié)構(gòu)，其安全性決定著整機(jī)的安全性。傳統(tǒng)可靠性求解方法為概率論和模糊理論描述不確定變量，概率論法和模糊理論需要獲知詳細(xì)的數(shù)據(jù)信息，而汽車起重機(jī)的生產(chǎn)批量小，不能收集到足夠的數(shù)據(jù)，容易得到不確定因素的界限。

Ben Haim Y 等[1]于1994年第一個提出基于凸集合模型的非概率可靠性理論；Ben-Haim Y 等[2]根據(jù)非概率可靠度定義研究結(jié)構(gòu)的非概率可靠性，認(rèn)為非概率可靠性指標(biāo)是一個區(qū)間；郭書祥等[3]將結(jié)構(gòu)的不確定參數(shù)描述成區(qū)間變量，使用非概率可靠性理論進(jìn)行了結(jié)構(gòu)可靠性研究；王欣等[4]對輪式起重機(jī)的箱形臂架進(jìn)行了非概率可靠性優(yōu)化；王睿星等[5]對4種主要的結(jié)構(gòu)非概率可靠性模型進(jìn)行了比較；楊淑偉等[6]首次對起重機(jī)臂架結(jié)構(gòu)進(jìn)行了凸模型非概率可靠性分析；劉麗等[7]對履帶式起重機(jī)進(jìn)行了區(qū)間非概率可靠性分析。

由于汽車起重機(jī)臂架區(qū)間非概率的研究不多，本文將汽車起重機(jī)的起升載荷、沖擊系數(shù)、偏擺角作為載荷的不確定性，確定臂架結(jié)構(gòu)強(qiáng)度、剛度、穩(wěn)定性可靠性計算準(zhǔn)則，建立區(qū)間非概率可靠性模型，并用工程實(shí)例來驗(yàn)證其正確性。

1 區(qū)間分析方法

1.1 區(qū)間分析的基本概念

不確定變量a為有界限的變量，其上界限為a1，下界限為a2，滿足a∈A＝[a1，a2]（A為總向量集合）稱a為區(qū)間變量。通過標(biāo)準(zhǔn)化轉(zhuǎn)化有

式中：ac為a的均值，ar為a的離差，δ為標(biāo)準(zhǔn)化區(qū)間變量取值為[-1,1]。

1.2 非概率可靠性分析方法

設(shè)向量X＝（x1，x2，…，xn）為與結(jié)構(gòu)相關(guān)的基本區(qū)間變量集合，xi∈X（i＝1，2，…，n）。取M＝g（X）＝g（x1，x2，…，xn）為結(jié)構(gòu)的功能函數(shù)。設(shè)其均值用Mc表示，離差用Mr表示，結(jié)構(gòu)的非概率可靠性為η＝Mc/Mr。由結(jié)構(gòu)可靠性理論可知，超曲線g（X）＝0表示失效面，結(jié)構(gòu)的基本參數(shù)空間被失效面分為失效域與安全域2部分，當(dāng)M＝g（X）＜0時結(jié)構(gòu)屬于失效的，當(dāng)M＝g（X）＞0時結(jié)構(gòu)屬于安全的。

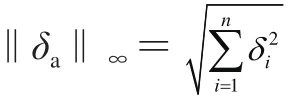
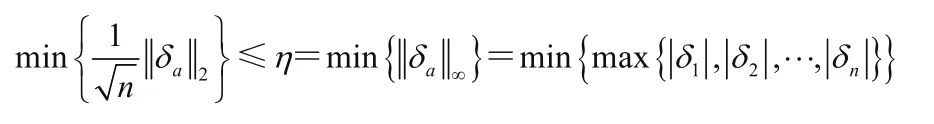
只有在g（δ1，δ2，…，δn）＝0和|δ1|＝|δ2|＝…＝|δn|時等式才成立。

2 汽車起重機(jī)臂架結(jié)構(gòu)非概率可靠性

2.1 臂架結(jié)構(gòu)區(qū)間變量及運(yùn)算

本文將臂架中存在的額定起升載荷Q、起升沖擊系數(shù)φ1，起升載荷的偏擺角φ作為不確定量，用區(qū)間表示為Q∈[Ql，Qu]、φ∈[φl，φu]、φ∈[φl，φu]可根據(jù)區(qū)間均值和離差公式求出這3個不確定區(qū)間變量的均值和離差分別為Qc、Qr、φc、φr、φ1c、φ1r，然后進(jìn)行標(biāo)準(zhǔn)化變換得到

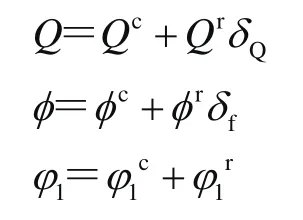
本文中相關(guān)的區(qū)間變量所受力和力矩標(biāo)準(zhǔn)化公式為

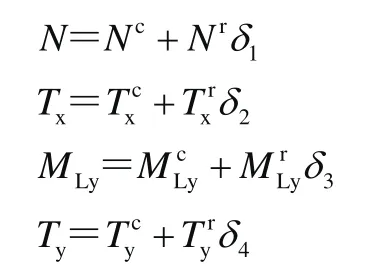
式中：δ1、δ2、δ3、δ4為相應(yīng)變量的標(biāo)準(zhǔn)化區(qū)間變量值。

2.2 臂架的整體非概率穩(wěn)定性功能函數(shù)

臂架整體穩(wěn)定性失效準(zhǔn)則確定的功能函數(shù)為

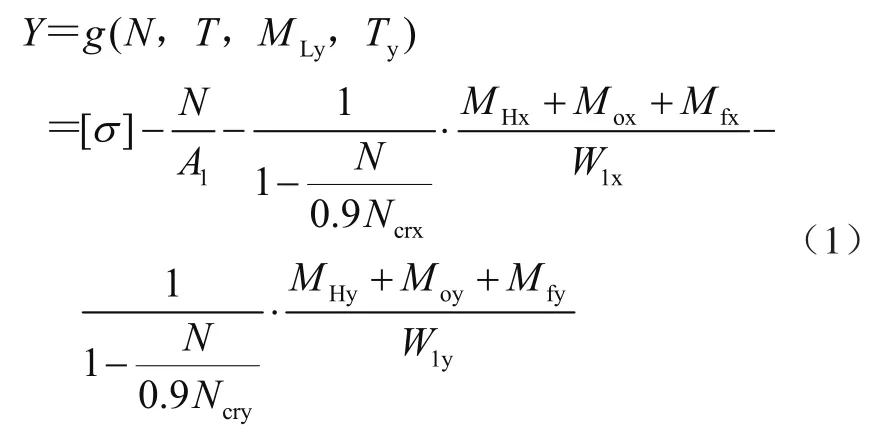
式中：[σ]為許用應(yīng)力，A1為基本臂截面積，W1x、W1y為基本臂抗彎模量，Ncrx、Ncry為變幅回轉(zhuǎn)平面的臨界力，MOx、MOy為臂架端部彎矩，MHx、MHy為橫向載荷在變幅回轉(zhuǎn)平面的最大彎矩，Mfx、Mfy臂架間隙撓度產(chǎn)生的彎矩。

由式（1）可得

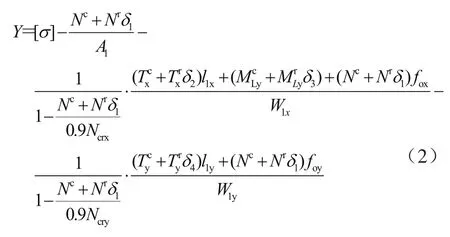
非概率可靠性指標(biāo)定義為

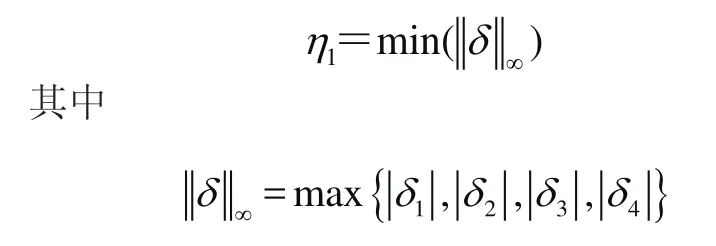
2.3 臂架強(qiáng)度非概率可靠性功能函數(shù)

臂架z處的強(qiáng)度非概率可靠性功能函數(shù)為

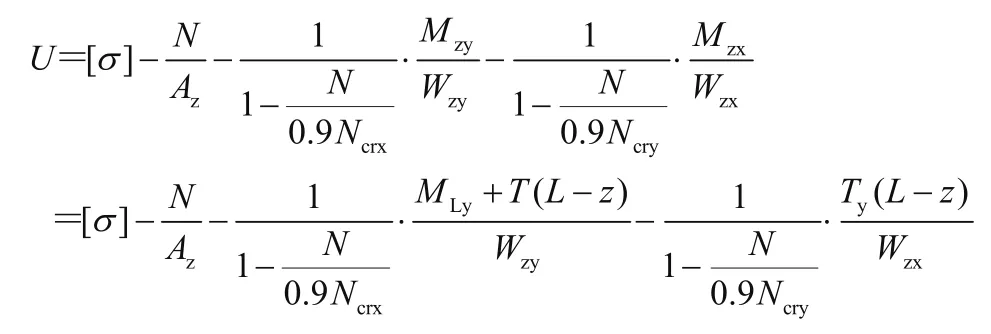
式中：Mzy、Mzx為橫向載荷在變幅回轉(zhuǎn)平面產(chǎn)生的截面彎矩，Wzy、Wzx為斷面抗彎模量。

結(jié)合上式可得

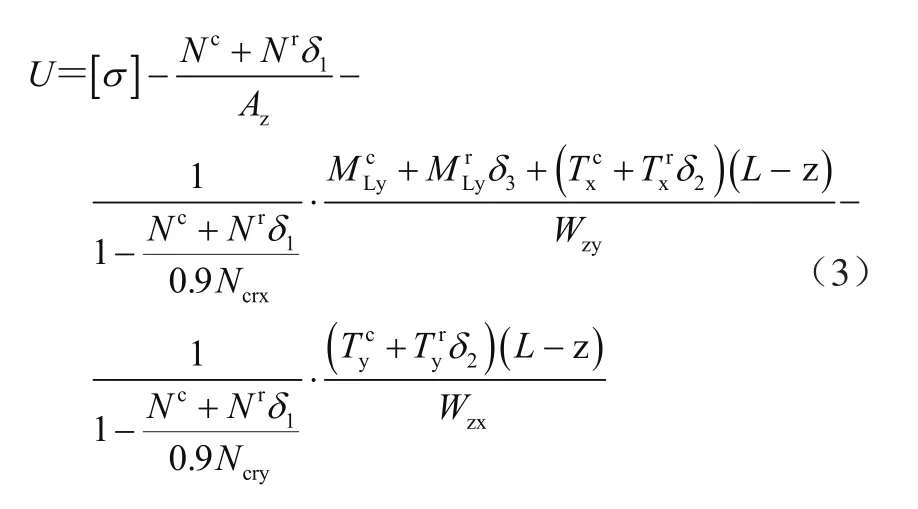
非概率可靠性指標(biāo)定義為

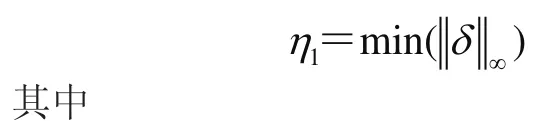
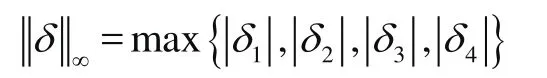
2.4 臂架的剛度非概率可靠性功能函數(shù)

臂架在變幅平面的剛度非概率可靠性功能函數(shù)為

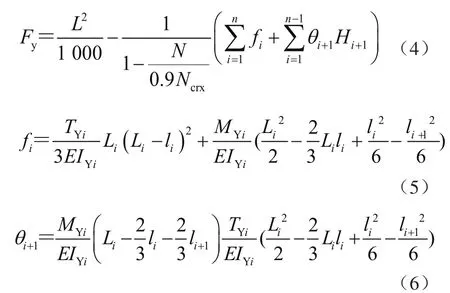
回轉(zhuǎn)平面的剛度非概率可靠性功能函數(shù)為

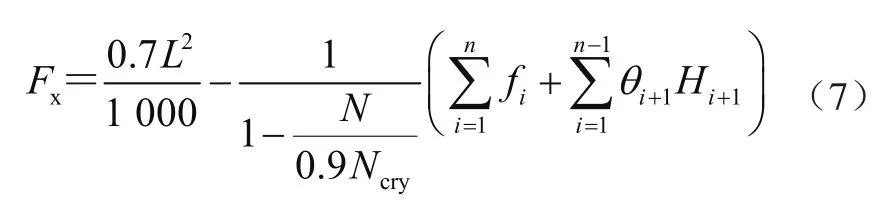
3 工程實(shí)例

對某25 t汽車起重機(jī)臂架進(jìn)行可靠性分析，選取得起重機(jī)臂架總長L＝32 400 mm，臂架材料為HG60鋼，屈服強(qiáng)度σs＝460 MPa，抗拉強(qiáng)度σb＝570 MPa，計算選擇最危險的工況，伸縮臂全伸，臂架幅度為5.5 m，起升角度為θ＝81o，額定起升載荷為6 t。起重量的變化區(qū)間為Q∈[50，60] kN，起升沖擊系數(shù)φ1∈ [0.85，1.15]，偏擺角φ∈ [2o，5o]，根據(jù)公式可以得到軸向力F∈[102.2，119.7] kN，橫向力Tx∈[12，13.8] kN，載荷偏心引起的彎矩MLy∈ [2.3×107，2.9×107] N · mm，回轉(zhuǎn)平面所受的側(cè)向載荷Ty∈[2.7，6] kN。計算參數(shù)如表1所示。

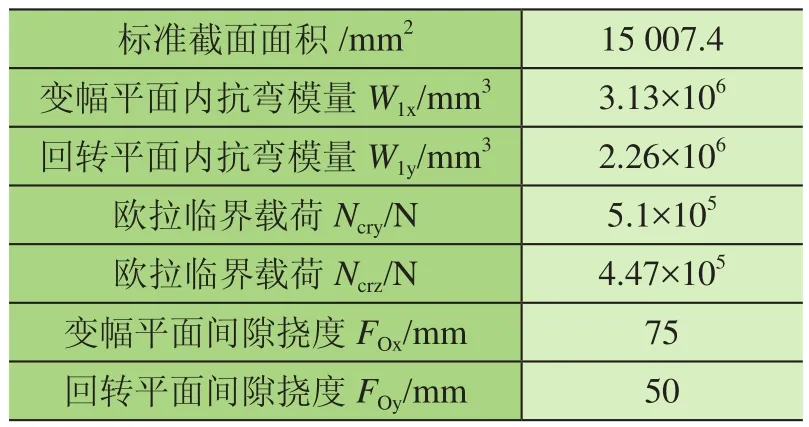
表1 臂架主臂截面性質(zhì)

將實(shí)例中區(qū)間變量標(biāo)準(zhǔn)化，即有

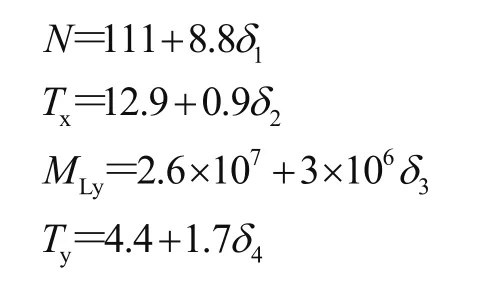
3.1 臂架的穩(wěn)定性非概率可靠性計算

在此工況下，n＝1.33，則許用應(yīng)力為

將表中1數(shù)據(jù)帶進(jìn)來得到結(jié)果，令Y＝0，得到η1＝1.6669 07＞1，可知道此臂架得整體穩(wěn)定性是可靠的。

3.2 臂架的強(qiáng)度非概率可靠性計算

由臂架強(qiáng)度失效準(zhǔn)則可知，以往的力學(xué)分析和臂架受力特點(diǎn)可選取每節(jié)臂的搭接處截面和第一節(jié)臂與變幅液壓缸的交點(diǎn)處截面為最危險截面進(jìn)行臂架強(qiáng)度失效分析（見圖1），臂架計算截面參數(shù)見表2。

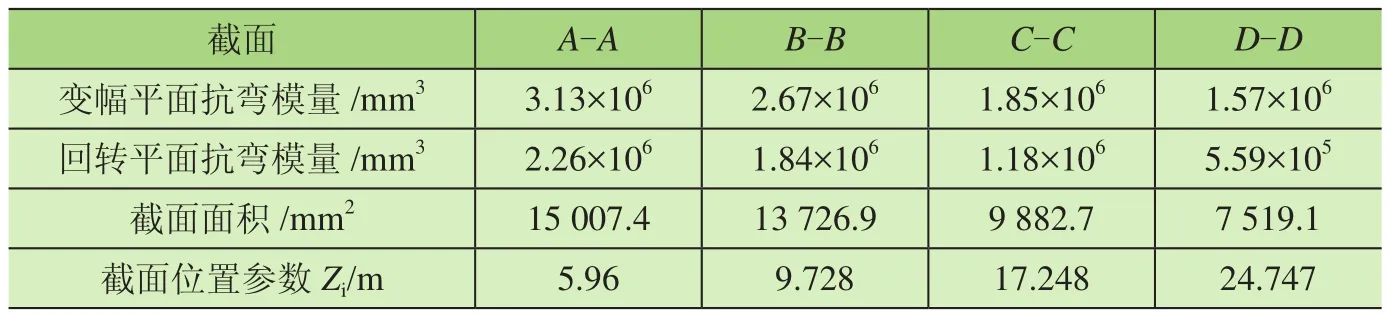
表2 臂架計算截面參數(shù)

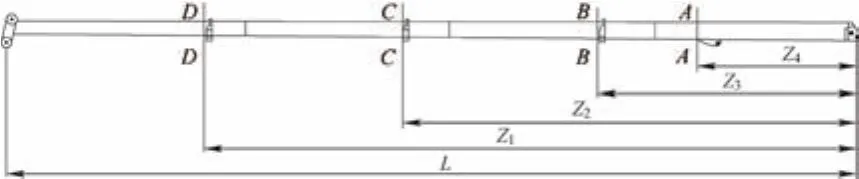
圖1 臂架強(qiáng)度危險截面

將相應(yīng)的數(shù)據(jù)帶到式（3）可得：ηA＝1.854 1，ηB＝1.644 9，ηC＝1.457 5，ηD＝2.377 5。由計算結(jié)果可知，該臂架的強(qiáng)度非概率可靠性是安全的。

3.3 臂架的剛度非概率可靠性計算

臂架的剛度非概率可靠性計算公式為

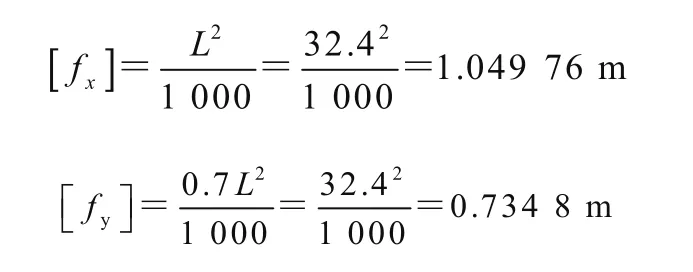
臂架計算長度參數(shù)為：L＝32 400 mm，L1＝9 728 mm，L2＝9 628 mm，L3＝9 159 mm，L4＝9 170 mm，H1＝ 26 400 mm，H2＝ 22 672 mm，H3＝ 15 152 mm，H4＝7 653 mm，l1＝5 270 mm，l2＝ 2 108 mm，l3＝1 660 mm，l4＝1 517 mm。將以上參數(shù)代入到功能函數(shù)公式中，即可得出變幅平面剛度非概率可靠度為η2＝1.146 3，回轉(zhuǎn)平面剛度非概率可靠度為η3=1.205 1，由此可知該臂架滿足整體的剛度穩(wěn)定性。

4 結(jié)論

1）由區(qū)間非概率可靠性方法對工程實(shí)例進(jìn)行計算得出臂架的穩(wěn)定性、強(qiáng)度、剛度可靠性結(jié)果均大于1，可知該臂架結(jié)構(gòu)處于安全狀態(tài)，用此方法只需知道不定量參數(shù)的集合界限，而無需知道大量樣本信息彌補(bǔ)了缺少實(shí)驗(yàn)數(shù)據(jù)的問題，對臂件的內(nèi)部結(jié)構(gòu)無要求。

2）由對工程實(shí)例的計算可知，用區(qū)間非概率可靠性的方法計算汽車起重機(jī)可靠性問題只需知道額定起重量、起升沖擊系數(shù)、起升載荷偏擺角度這些不確定量的區(qū)間，就可計算出結(jié)構(gòu)的可靠性指標(biāo)。