成品煙箱自動裝車系統垛型算法

徐躍明 方錦明 劉哲賢 鄭 重 陶海旭

1紅云紅河煙草（集團）有限責任公司 昆明 650202 2昆船智能技術股份有限公司 昆明 650236 3清華大學精密儀器系 北京 100084

0 引言

隨著物流自動化的發展，智能立體倉儲和自動化分揀設備得到了廣泛應用，但貨車運輸前的裝車過程卻仍然高度依賴人工，國內目前暫無成熟的自動裝車系統。裝貨車依賴人工的主要缺點有：自動化、信息化程度低；成本高，管理難度大；效率低，很難長期保持高效率作業；缺少產品數據有效追溯；招工困難，愿意從事搬運行業的年輕人越來越少。除煙箱物流外，疫情之下的冷鏈物流行業對自動裝車系統也有同樣迫切的需求。

理論研究中把這類問題稱為集裝箱裝載問題（CLP）。集裝箱裝載問題是一個經典的組合優化問題：給定一些不同規格的三維箱子，將箱子的1個子集裝載進集裝箱，使得集裝箱的空間使用率最大。集裝箱裝載問題是一個NP -難的問題[1]：它是背包問題(Knapsack Problem)在三維空間上的擴展。由于背包問題本身是NP完全問題，故集裝箱裝載問題也不存在有多項式時間復雜度的算法。出于問題本身搜索空間的龐大，求解精確解的集裝箱裝載算法通常只能求解小規模的問題[2]。

Junqueira L等[3]在2012年使用混合整數線性規劃模型來求解集裝箱裝載矩形箱的最優解，并考慮了貨物穩定性和負載的約束。其使用優化軟件對100多個隨機生成的實例進行了全面的性能分析[4]。計算結果驗證了這些模型，并表明它們只能夠處理中等規模的問題。該方法的問題在于計算量過大，無法適應實際使用場景。Zhu W等[5]提出了一種分析框架來描述基于塊構建的方法。該框架是基于大多數方法中存在的6個共同要素。(K1)容器中自由空間的表示；(K2)生成塊的機制；(K3)用于對自由空間進行排序的啟發式方法；(K4)用于對盒子進行排序的啟發式方法；(K5)用于決定如何將選定的塊放在選定的自由空間中的啟發式方法，以及(K6)整體搜索策略。Araya I等[6]在2014年基于塊構建的方法，提出了BSG-CLP搜索策略。BSG-CLP是一種基于Beam搜索的算法，其使用基于Greedy的函數來評估搜索圖中的狀態。Beam搜索可被看作是對分支和邊界搜索的改編，在搜索圖的每一層只擴展最有希望的節點的子集[7]。綜上所述，針對成品煙箱自動裝車系統垛型算法選擇基于塊構建的Beam搜索算法。

1 理論建模

針對實際煙箱碼垛問題進行數學建模，并對一些限制條件進行量化。整車廂為點集A，長寬高依次為L、W、H，鵝頸板尺寸依次為a、b、c。訂單順序為集合Sj。

Sj=（li，wi，hi，nj）

式中：j為第j個訂單；li，wi，hi為該品種煙箱長、寬、高；nj為數量。

操作集合為

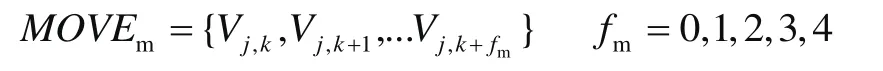
式中：Vj，k為煙箱，1≤k≤nj；xj，k，yj，k，zj，k為左下頂點坐標。

優化目標為

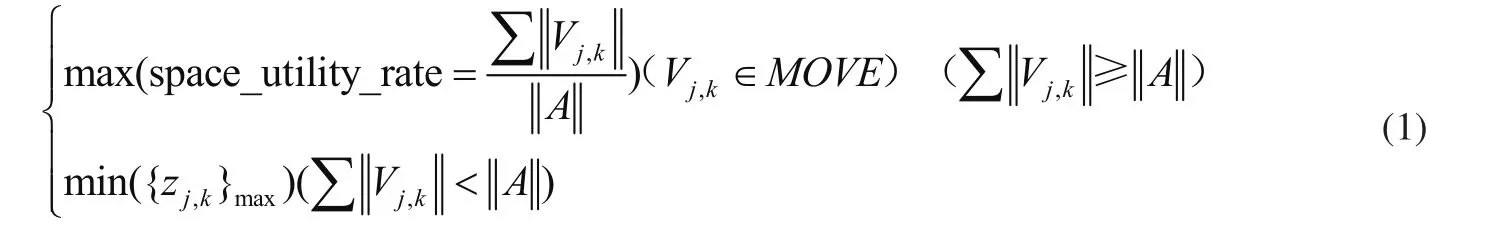
下面給出了5點垛型設計數學模型中最基本的限制條件：

1）任意2個煙箱不重疊，即有

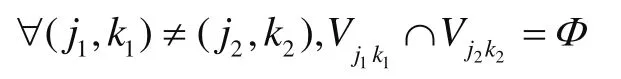
2）不同種類的煙箱盡可能依照順序從里向外從下向上擺放，即有

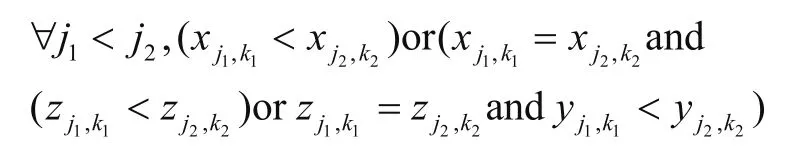
3）煙箱包含在車內，即有

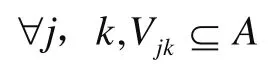
4）一次碼放的煙箱只能在一橫排上。即有

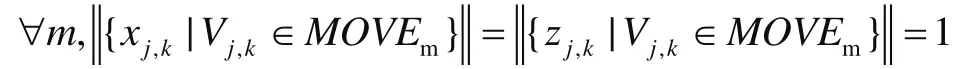
5）碼放煙箱的平均時間小于閾值，即有

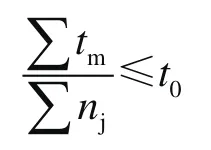
2 Beam Search算法

一般的搜索過程中，每一個狀態都會拓展出很多個新狀態，新狀態又會拓展新的狀態。如果采用全局搜索的方法，計算開銷和狀態的存儲開銷非常大。而采用Beam Search的算法，例如在搜索寬度是2的情況下，對初始狀態拓展出2×2=4個新的狀態，對這4個新狀態分別做出評價，然后取評價最高的2個狀態，分別各拓展出2個新狀態；再對4個新狀態進行評價，以此類推。因此，Beam Search的計算量遠小于全局搜索，且通過調整搜索寬度又可保證一定的搜索空間，通過狀態評價來盡可能地趨近較優解。Beam Search算法流程圖如圖1所示。

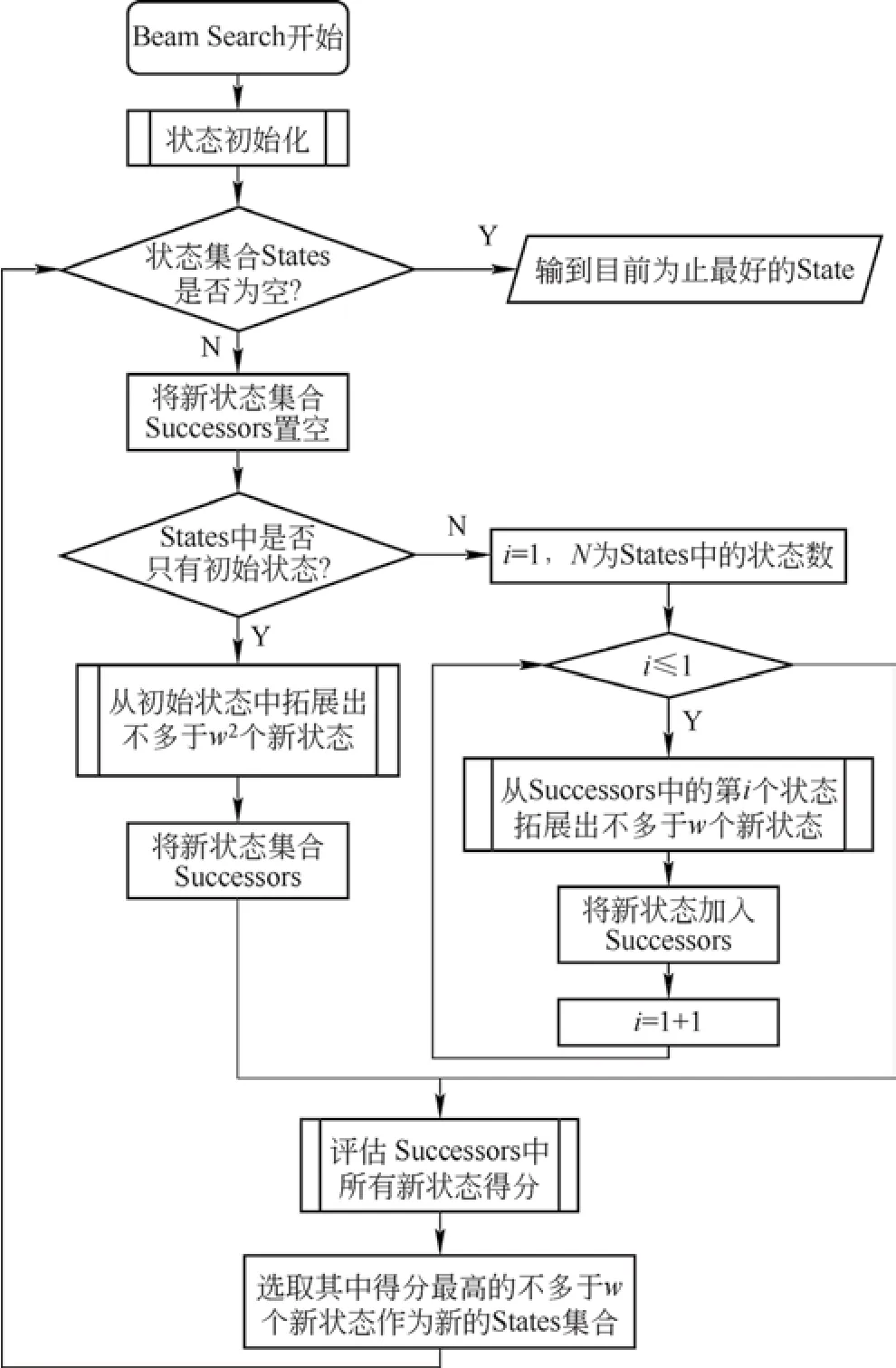
圖1 Beam Search算法流程圖

2.1 利用簡單算法對人工碼垛的復現

為了顯示Beam Search算法的結果并驗證其正確性，需完成1套簡單的垛型仿真平臺，在算法之外實現對車廂空間的還原。首先對人工碼垛的思路進行復現，然后再嘗試使用Beam Search等方法。

簡單算法參考人工碼垛時的經驗，采取“碼墻”的辦法，即由內至外一面墻一面墻的進行碼垛。具體每一面墻碼放方式為：首先將相同尺寸、相同姿態的煙箱從車廂的左下角開始盡可能地放入墻中，直到不能繼續放入。此時車廂右側或上方還可能留有部分空余空間，再將該煙箱調整姿態，盡可能地放入車廂空余空間中，直到不能繼續放入。如果該類煙箱仍有剩余，則開始下一面墻的碼放，方式同上。如果該類煙箱在上述擺放過程中就已經放完，則開始下一品規煙箱的擺放，方式同上。依次類推，直到將車廂擺滿或者煙箱被全部放入。當同一面墻中擺入了不同品規的煙箱時，其不同位置處的厚度不一樣，取每面墻的最大厚度為該面墻厚度。下一面墻將從最大厚度處開始碼放，故墻與墻之間可能會存在空余空間。

通過實際訂單情況的檢驗，簡單算法在設計平板車垛型時一般也能達到較高的空間利用率，且簡單算法所設計出的垛型結構簡單，易于裝車。但由于墻與墻之間可能存在一定的空余空間（見圖2），運輸過程中垛型容易發生滑移甚至部分倒塌，其穩定性不夠。且無法針對鵝頸板長度調整垛型設計，難以適應鵝頸板車的情況。故嘗試使用Beam搜索的方式來設計垛型。

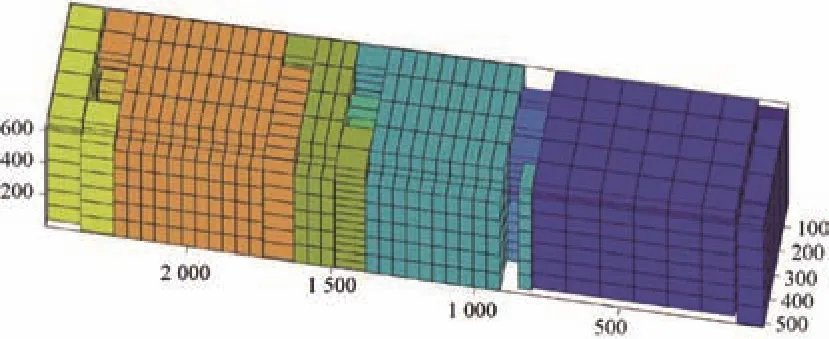
圖2 簡單算法垛型設計圖（無鵝頸板）

2.2 Beam Search算法狀態表示

搜索過程中的狀態由4個基本部分組成：1）剩余箱子的集合Remaining Boxes，即還有哪些箱子需要被放入車廂；2）空余空間的集合 Empty Spaces，即還有哪些地方可以放箱子；3）當前可選的煙箱塊Available Blocks；4）已經碼放完成的箱子順序和位置的記錄Moves。最難表示的是空余空間集合。

如圖3所示，把1個立方體放入空的立方體空間后，剩余的空間是不規則的立體圖形。使用重疊的長方體集合（Empty Maximum Spaces）：對每個箱子，以其1個面為分界面，向空的方向最大延伸的長方體。如圖3a中的空余空間可由圖3b～圖3d中3個透明空間表示。

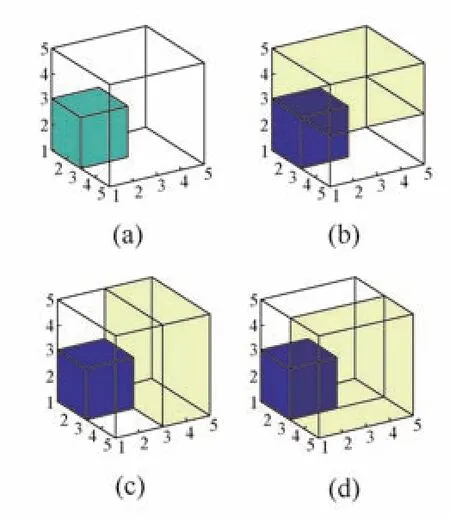
圖3 Empty Maximum Spaces示意

具體到算法中，圖4中的紫色透明長方體就是從已經碼放好的箱子的面上向外延伸的最大的空長方體。

圖4 實際狀態中的剩余空間表示

2.3 Beam Search算法狀態拓展

簡單來說，搜索過程中的狀態轉移過程是搭積木的過程，每次選擇1個空余空間、選擇由多個箱子組成的Block，然后將Block放入空余空間中并更新狀態。

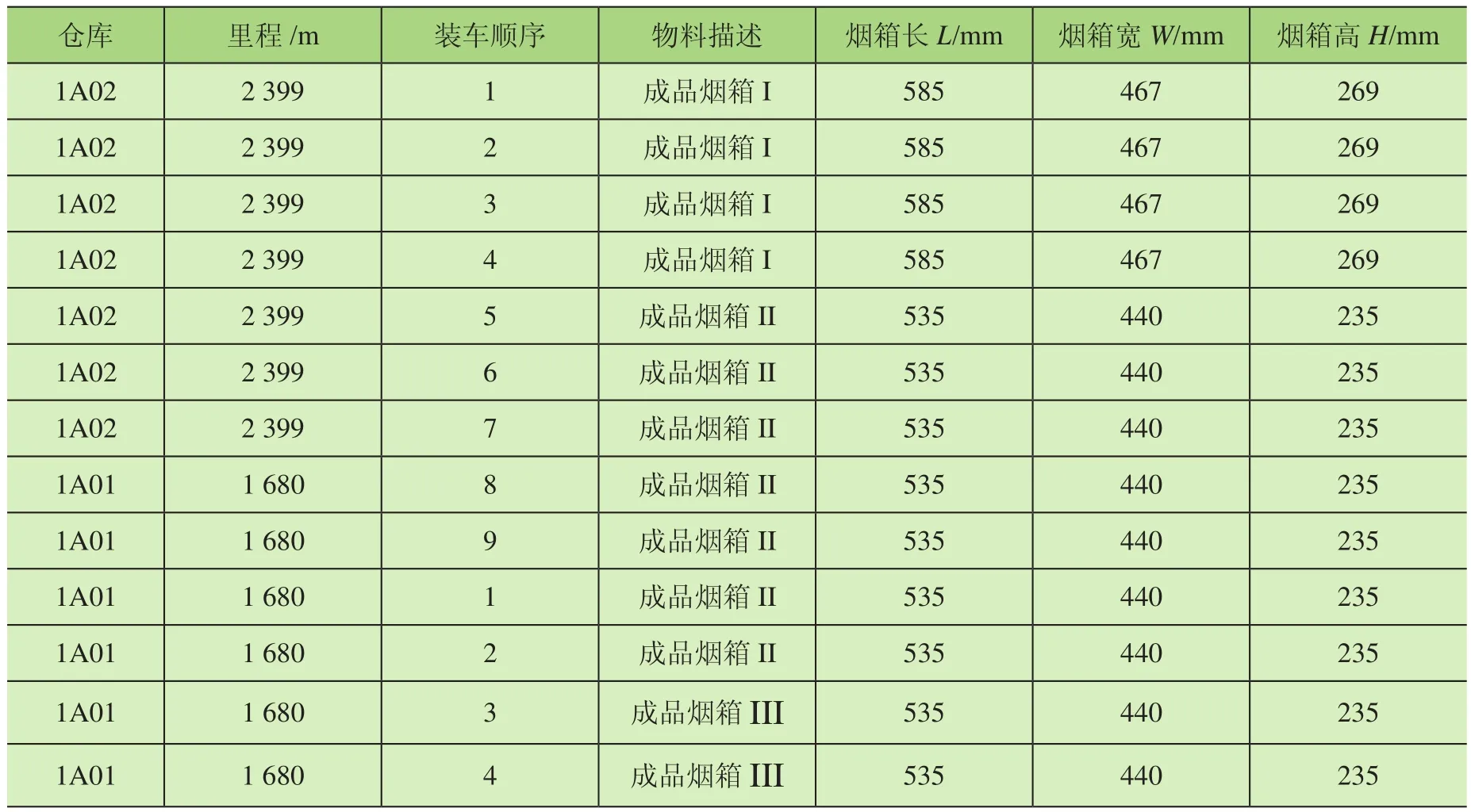
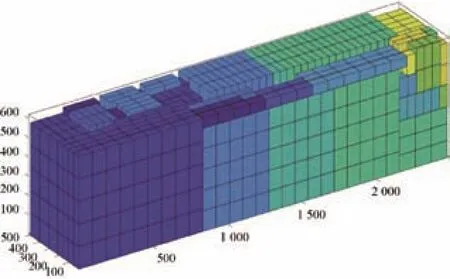
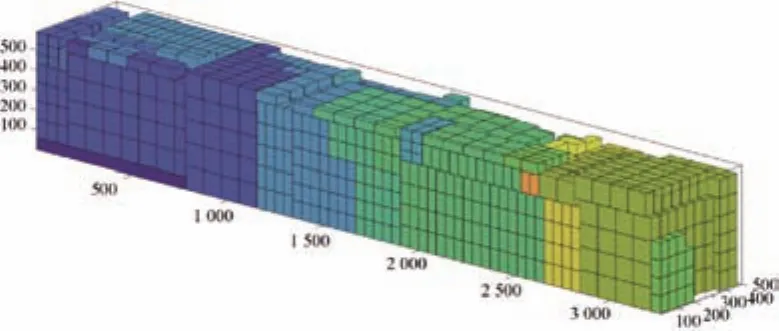
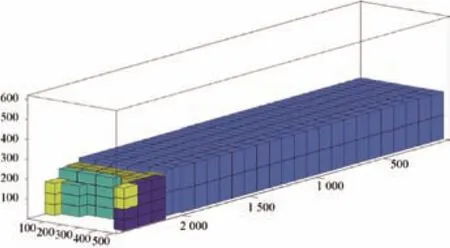
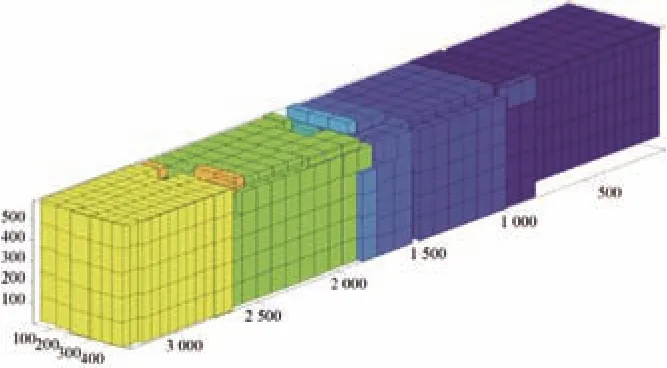
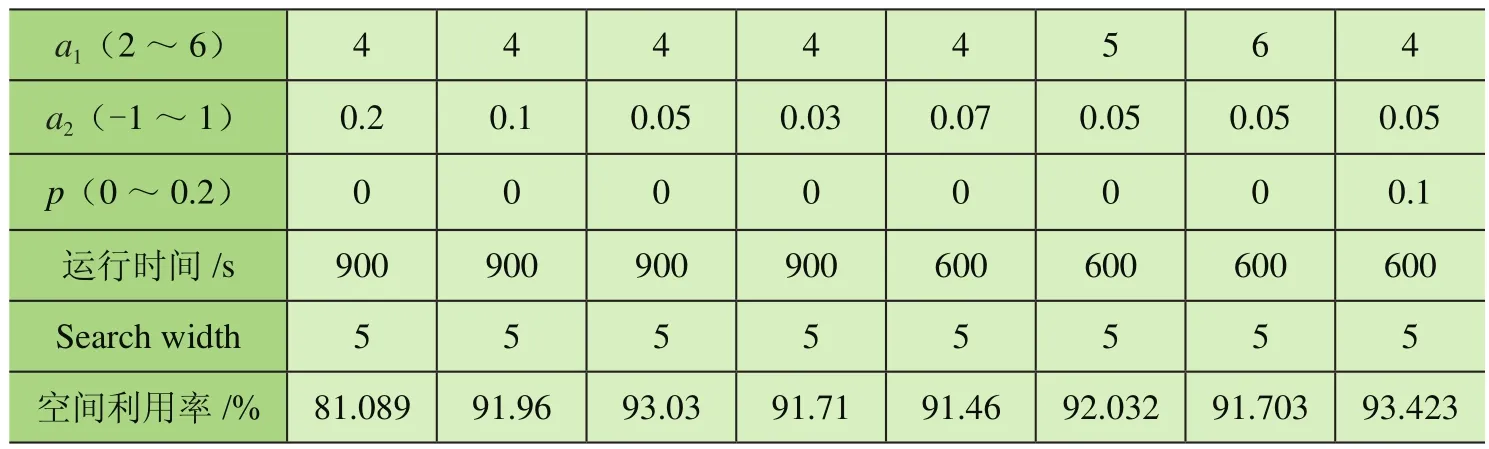
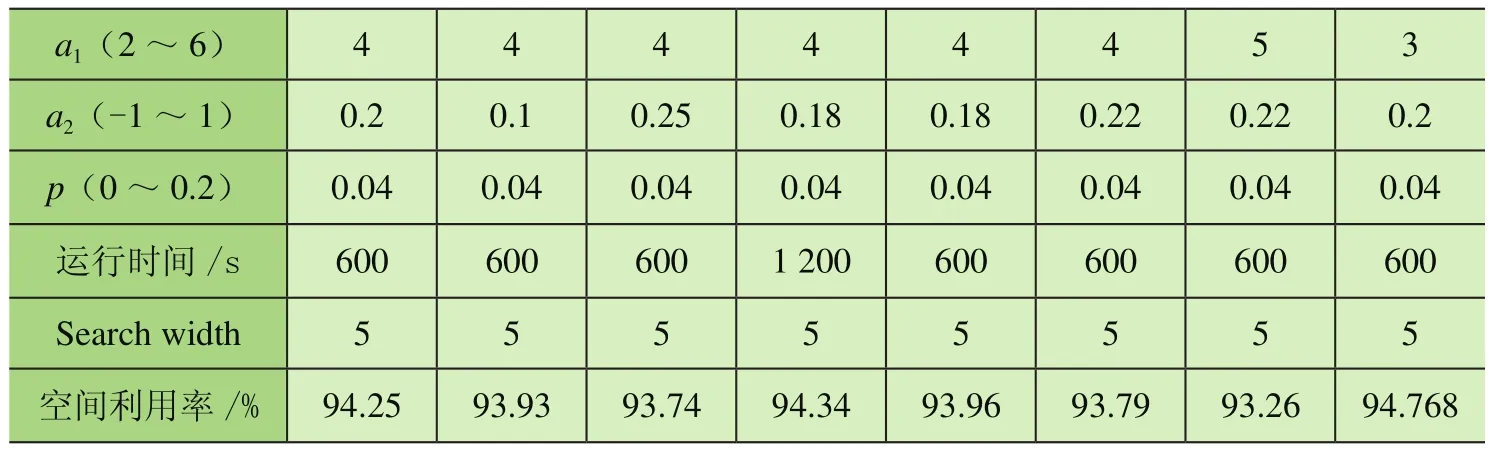
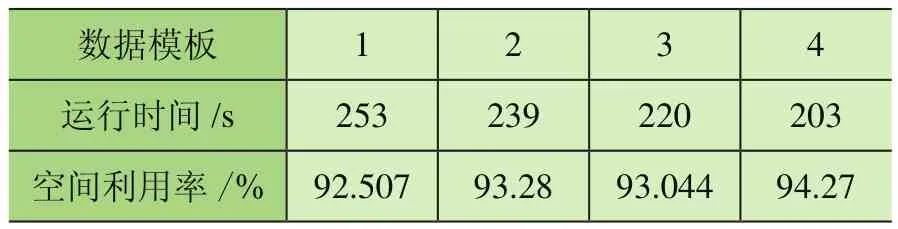
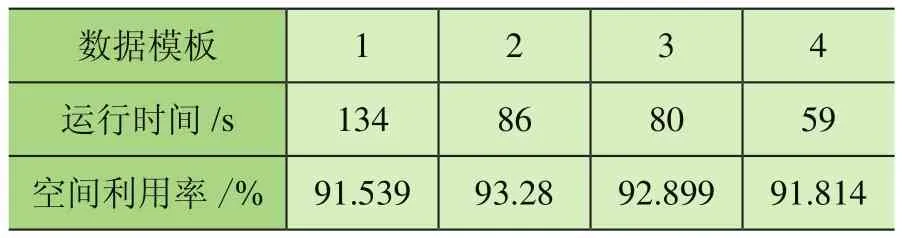
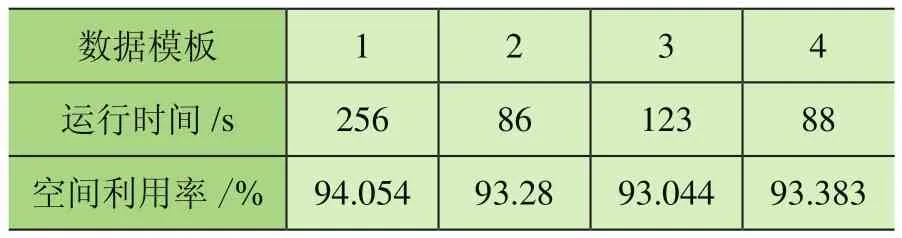
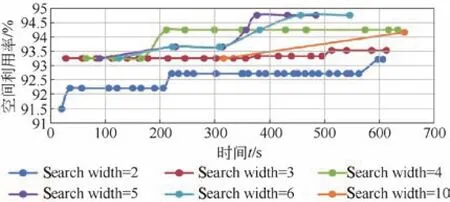
在選擇空余空間時采用加權曼哈頓距離對可選空間進行評價排序，取出優先級最高的空間。加權曼哈頓距離為：distance=w_1X+Z+w_2Y；其中，w_1

在選定待放入煙箱和空余空間后需要對狀態進行更新。從剩余箱子的集合中減去Block包含的箱子，從空余空間集合中刪掉放入箱子的空間，并加入新產生的空間，其中需要處理空間相互包含的情況，同時如果前面選擇了空余空間后遍歷所有塊都無法放入，則刪除該空間，如果煙箱塊需要的煙箱數量大于剩余煙箱，則在可選的煙箱塊集合中刪除該塊，最后在Moves中記錄下這步操作，完成狀態拓展過程。

2.4 Beam Search算法狀態評價

在Beam Search的過程中，每拓展一些新狀態，就要對新狀態進行一次評價，以挑選出當前認為最好的幾個狀態。采用的評價過程為：使用貪心算法來得到完整解，即從當前狀態出發進行搜索寬度為1的搜索，不斷拓展狀態直到車廂被放滿。然后使用該完整解的空間利用率作為當前狀態的評價。

該方法可在搜索算法全部完成前就先得到完整解，多數情況貪心算法得到的完整解效果也能滿足實際需求。

2.5 垛型反推擺放順序

在設計完成垛型后，算法還需指導自動裝車完成碼垛工作，故需根據垛型來反推不同位置煙箱的碼放順序與位置。碼放順序原則為：

原則1：煙箱1左下坐標（x1，y1，z1），煙箱2左下坐標（x2，y2，z2）。若x1＜x2，則煙箱1先于煙箱2碼放；若x1=x2，z1＜z2，則煙箱1先于煙箱2碼放；若x1=x2，z1=z2，y1＜y2，則煙箱1先于煙箱2碼放。

原則2：放入某個煙箱時，該煙箱下底面與其他煙箱或車廂底面的接觸面積之和應大于下底面面積的90%；

原則1保證了已放入的煙箱不會對機械裝置發生干涉，原則2保證了裝入的煙箱具有足夠的支撐。此外，由于自動裝車的設計為每次可放入1排若干個煙箱，為了提高裝車效率，應盡可能每次將處在同一排的煙箱一起放入。算法流程如下：

1）先將垛型中所有煙箱按照原則1排定擺放順序，從先到后編號為1～N；

2）i=1～N，依次考慮第i個煙箱時，依據原則2判斷能否放入，若不能放入則進入等待序列；若能放入則進入擺放序列，并將等待序列中重新滿足原則2的煙箱進入擺放序列。

上述流程可滿足擺放要求，但會出現處于同一層的可一次性放入的煙箱順序被分散在擺放序列中。為了提高效率，在上述流程的第二步中，加入重新考慮等待序列的前提條件：當自動裝車恰好可以一次性放入其能力極限的煙箱個數時，再考慮等待序列中的煙箱能否進入擺放序列。

2.6 研究結果分析

2.6.1 系統輸入

系統輸入為裝有煙箱訂單數據的Excel表格，如表1所示。

表1 訂單數據表

2.6.2 系統輸出

根據車輛有無鵝頸板及訂單中煙箱總量是否超出單車裝載能力，系統的輸出可分為多種情況。圖5～圖8展示的4種垛型效果圖為：車輛無鵝頸板且訂單中煙箱總量超出單車裝載能力；車輛有鵝頸板且訂單中煙箱總量超出單車裝載能力；車輛無鵝頸板且訂單中煙箱總量小于單車裝載能力；車輛有鵝頸板且同品規煙箱集中放置。

圖5 垛型效果圖（無鵝頸板、訂單中煙箱總量超出單車裝載能力）

圖5最外側大長方體代表1個車廂，單個小立方體代表單個煙箱，同種顏色的小立方體代表同一訂單中同一品規的煙箱，圖6中左下角深藍色部分和圖8中右下角白色部分代表車輛鵝頸板。當訂單中煙箱總量超出單車裝載能力時，系統會以車廂空間利用率盡可能高為目標進行垛型設計。當訂單中煙箱總量低于單車裝載能力時，系統會在保證訂單中煙箱全部裝入車廂的基礎上考慮垛型在運輸過程中的穩定性，如圖7所示。

圖6 垛型效果圖（有鵝頸板、訂單中煙箱總量超出單車裝載能力）

圖7 垛型效果圖（無鵝頸板、訂單中煙箱總量小于單車裝載能力）

圖8 垛型效果圖（有鵝頸板、同品規集中放置）

3 參數測試與系統穩定性測試

3.1 系統參數測試

系統的評價函數中有許多超參數，例如評價過程中各影響部分的權重值，需要通過實驗確定其最佳取值。

表2和表3為評價函數中各參量不同取值對實驗結果的影響。其中a1為相鄰面積權重，a2為單個Block中煙箱個數權重，p為計算相鄰面積時的距離系數，Search width為搜索寬度。

表2 參數取值對結果的影響

表3 參數取值對結果的影響

從實驗結果中可知，當a1=3，a2=0.04，p=0.04時，相同情況下車廂的空間利用率最高。

3.2 系統穩定性測試

對于不同的訂單數據，程序運行結果呈現出一定的差異性，總體來看，程序對不同訂單輸入都有較好的效果，能滿足實際需求。從表2和表3可知，程序在不同數據輸入的情況下運行240 s左右設計出的垛型能達到92.5%以上的空間利用率。同時根據實際需求，一般要求裝車垛型至少達到90%的空間利用率，通過表4和表5可知，程序在不同數據輸入的情況下最長需要134 s達到該標準，對于某些特定訂單只需60 s左右即可滿足要求。表6展示了當空間利用率要求提高至93%時程序對于不同訂單數據所需要的運行時間。

表4 程序在相同參數下對不同訂單數據運行240 s左右結果（有鵝頸板）

表5 程序在對不同訂單數據達到90%空間利用率所需最短時間（有鵝頸板）

表6 程序對不同訂單數據達到93%空間利用率所需最短時間（有鵝頸板）

圖9和圖10依次展示了程序在不同搜索寬度下的垛型空間利用率隨時間變化曲線和程序對于不同訂單輸入下的垛型空間利用率隨時間變化曲線。

圖9 無鵝頸板不同搜索寬度下空間利用率隨時間變化曲線

圖10 不同訂單數據空間利用率隨時間變化曲線

由圖可知，不同搜索寬度下程序運行結果存在較大差異，當Search width取值大于3時總體效果較好。同時對于不同訂單信息輸入，程序的運行結果也存在一定的差異，但都能夠滿足90%空間利用率以上。

4 結論

基于Beam Search算法建立成品煙箱自動裝車系統算法的數學模型，通過簡單算法的仿真平臺顯示Beam Search算法的結果并驗證其正確性。通過參數測試得出當a1=3，a2=0.04，p=0.04時，相同情況下車廂的空間利用率最高。通過系統穩定性測試得出，不同搜索寬度下程序運行結果存在較大差異，當Search width取值大于3時總體效果較好。同時對于不同訂單信息輸入，程序的運行結果也存在一定的差異，但都能夠滿足90%空間利用率以上。