基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合方法?
黃志忠潘 漢
(1.桂林航天工業學院電子信息與自動化學院,廣西 桂林541004;2.上海交通大學航空航天學院,上海200240)
隨著星載傳感器技術的發展,高光譜、多光譜、可見光和紅外等傳感器得到了廣泛應用。然而,高光譜具有較高的光譜分辨率但是空間分辨率較低。多光譜圖像具較高的空間分辨率,然而光譜分辨率相對較低。全色圖像具有比較高的圖像空間分辨率。多模圖像融合通過集成多模敏感器的細節信息,可以綜合成高質量的圖像,提高圖像信息的利用率,可為后續的目標檢測與識別提供技術支撐[1-2]。
國內外針對圖像融合問題已經提出許多算法[3-5]。相對于融合類型來說,目前主要有高光譜與多光譜圖像融合、高光譜與全色圖像融合,以及多時相圖像融合等。然而,常用的圖像融合方法只能融合兩個模態傳感器的信息。與此同時,如果設計一個具有較好融合性能的正則化方法仍是一個比較重要問題。
目前,一種比較好的正則化方法是變分正則化方法[6]。該方法的成功之處在于可以保留圖像中的邊緣信息,但是會對圖像紋理過平滑,也就是階梯效應。雖然,文獻[3]提出了一種基于黎曼流形優化的多源多波段圖像融合方法。但是,多模圖像空間信息與頻譜信息的高階相關性及其內在結構特性還沒有得到充分的利用。
針對上述問題,本文基于圖像域的非局部自相似框架,引入復合正則化方法,提出了基于全局稀疏梯度與低秩張量正則化的多模圖像融合方法,并應用于多源多波段圖像融合,也就是高
光譜、多光譜與全色圖像的融合。
本文的主要工作歸納如下①研究了一種基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合模型,并給出相應的優化求解方法;其中,多源多波段圖像的頻譜信息使用全局稀疏梯度正則化方法,空間信息使用低秩張量正則化方法。②應用于多源多波段圖像融合,實現高光譜、多光譜與全色圖像的融合。仿真實驗驗證了該方法的可行性和有效性。
本文的主要結構如下:第1節給出了多源多波段圖像觀測模型,然后推導了基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合模型。第2節給出求解該模型的交替方向乘子法。第3節對所提方法進行驗證,并給出與其他方法的對比結果。
1 多源多波段圖像融合問題建模
1.1 多源多波段圖像觀測模型
本文使用文獻[3]中的觀測模型。本文使用Z∈RL×N表示高光譜圖像,L用于表示光譜波段數,N用于圖像相應的像素個數。
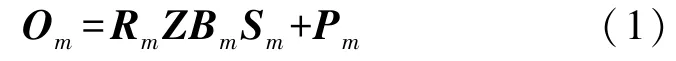
式中:Rk是光學傳感器產生的譜響應,其對應的觀測值是Om;Bm∈RN×N是與波段相對應的點擴散函數,也就是空間模糊矩陣。Sm是一個滿足STmSm=IN的稀疏矩陣。Pm是加性擾動矩陣,代表著與成像傳感器相關的噪聲。
1.2 基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合模型
本小節引入復合正則化方法,考慮多模圖像的全局稀疏梯度正則化方法,以及低秩張量正則化方法,給出基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合模型。本文使用線性混合模型[7](Linear mixture model)表征觀測場景中的成像數據。給定的端元數目記為Q,且滿足Q?L,將Q個端元構建為E∈RL×Q的列,那么可將Z分解為:

式中:A∈RQ×N是端元豐度矩陣,P是相應的加性擾動矩陣。
將式(2)代入(1),我們可以得到:
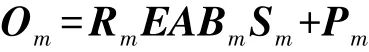
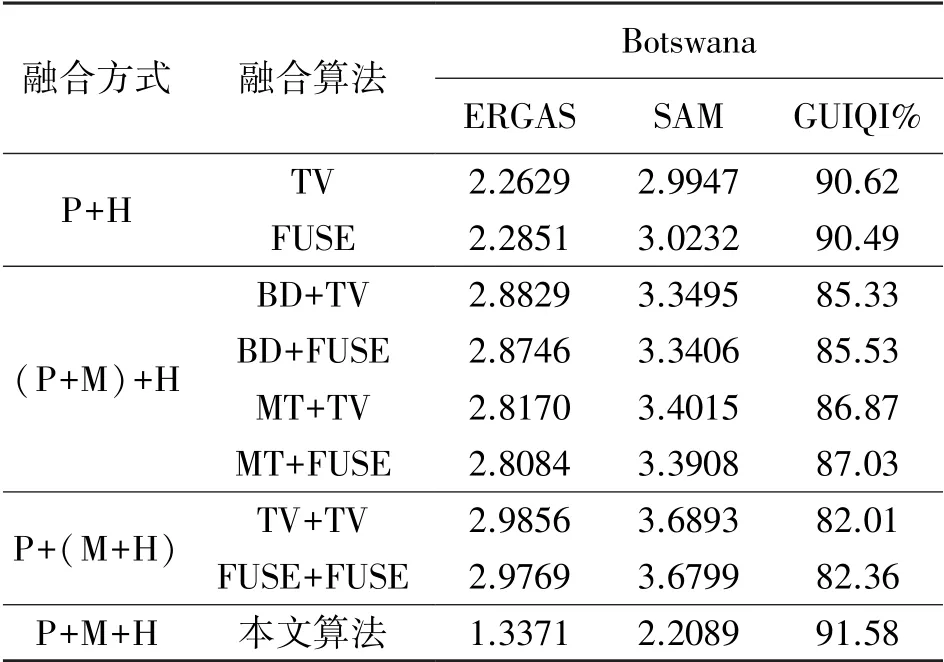
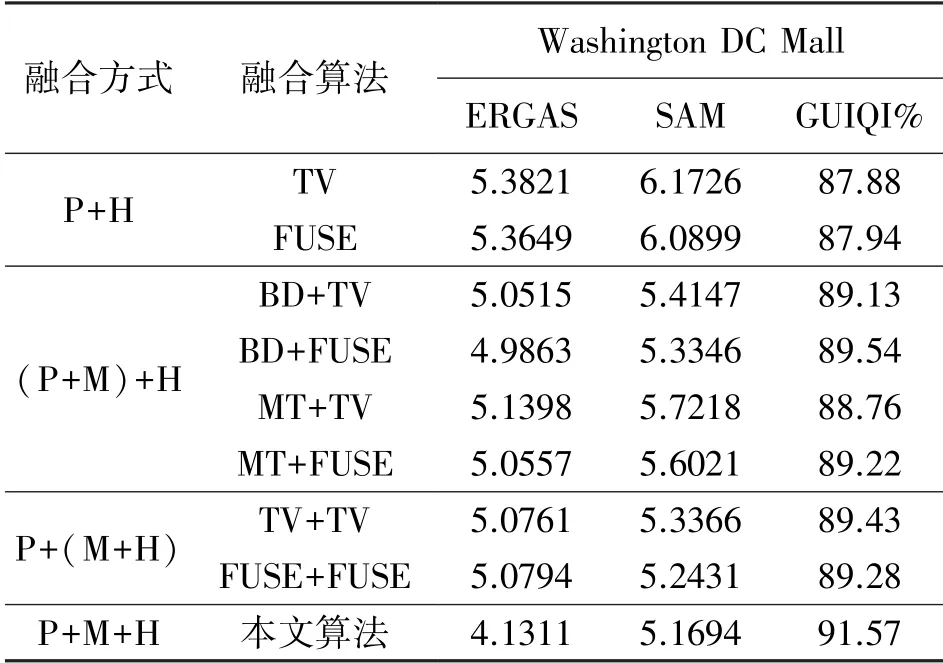
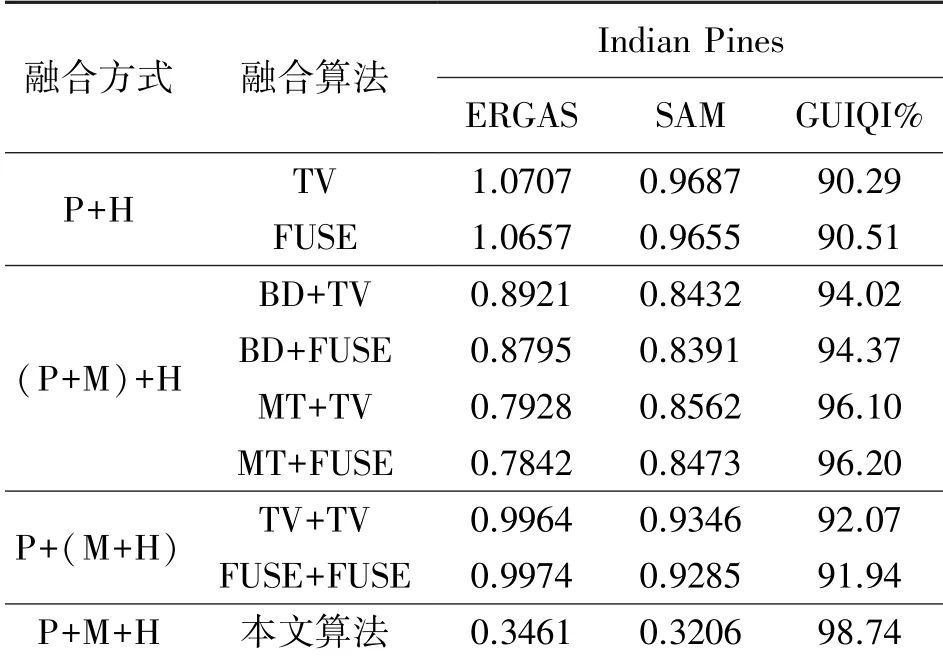
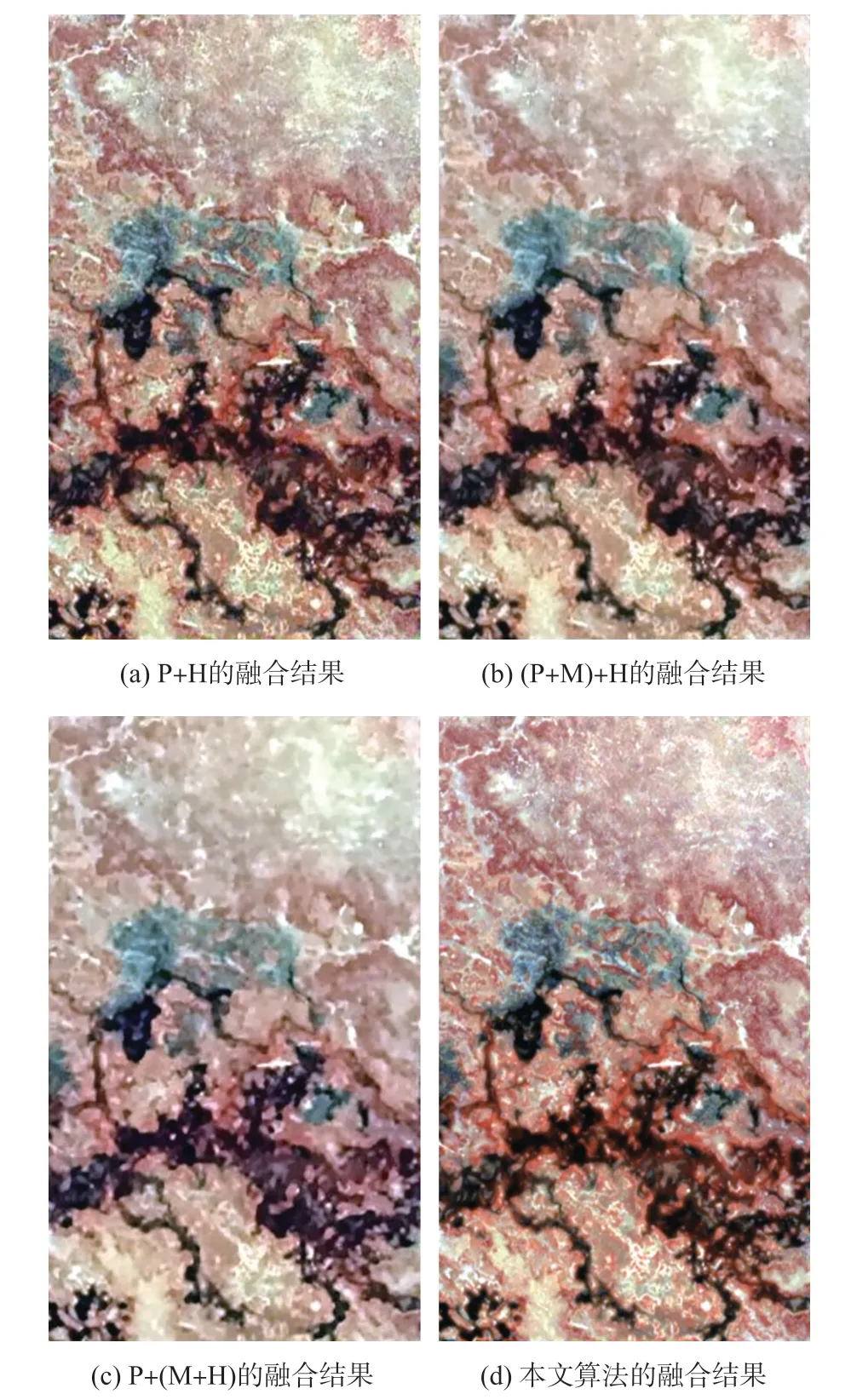
為實現任意空間分辨率和光譜分辨率情況下的多源多波段圖像的融合,本文使用下面的多種正則化方法:①對A施加非負及系數和為1的約束,也就是A≥0且1TQA=1TN;②對A使用全局稀疏梯度正則化方法,也就是‖?cA‖p;其中,?c代表著沿著光譜方向的全局稀疏梯度正則化方法;此外,0 最后,本文給出基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合模型: 式中:α>0和β>0分別是相應正則化項的非負正則化參數。 本文使用交替方向乘子法(Alternating direction method of multipliers,ADMM)求解問題(3)。其中主要思想是變量分離策略,也就是引入輔助變量Um∈RQ×N(m=1,2,…,M)、V、W,以及K。在此基礎上,考慮A具有非負且系數和為1的約束,引入下面的示性函數: 本文提出的算法流程,如表1所示。 表1 基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合算法流程 為了驗證本文算法的有效性,我們考慮全色圖像、多光譜圖像和高光譜圖像,通過數值仿真的方式評估融合性能。本文的仿真實驗使用二個遙感數據集:Botswana(400×240×145)、Washington DC Mall(400×300×191),以及Indian Pines(400×400×200)。其中,400×240×145代表著遙感數據集的空間分辨率是400×240,波段數是145。本文的所有仿真實驗及算法運行環境是基于Intel CPU i7-9750H 2.6 GHz和8 GB內存的筆記本電腦。所有的算法使用MATLAB語言編程。 基于上述的遙感數據,為了生成高光譜圖像,本文對所輸入的圖像二維高斯模糊核(13×13,方差=2.12)進行卷積操作,然后對所產生的圖像以4的比率進行下采樣。為了生成多光譜圖像,本文首先將二維高斯模糊核(7×7,方差=1.06)應用于輸入的圖像數據集,以2的比率進行下采樣,最后使用Landsat 8多光譜傳感器的光譜響應特性進行圖像降質。另外,本文對所生成的圖像加入高斯噪聲,并使得所產生的多光譜和高光譜圖像的信噪比分別是30 dB。與此同時,全色圖像的信噪比設置為40 dB。 已有的多波段圖像融合算法僅能實現對兩個傳感器的圖像融合,例如多光譜圖像與高光譜圖像融合、全色圖像與多光譜圖像融合等。為了進行對比分析,本文使用相關的融合算法實驗三個傳感器圖像的融合。首先,本文使用二種多光譜圖像與全色圖像融合算法:①基于局部參數估計的波段相關空間細節算法[11](Band-dependent spatial detail,BD);②基于高通調制的調制傳輸函數廣義拉普拉斯金字塔算法[12](Modulation-transfer-function generalized Laplacian pyramid,MT)。 本文使用兩種算法進行多光譜圖像與高光譜圖像的融合:①基于全變分正則化及子空間的融合方法[6](Total variation,TV);②基于Sylvester方程的快速融合方法[13](Fast fusion based Sylvester equation,FUSE)。 為了評估算法的融合性能,本文使用常用的三種評估指標:①相對無量綱全局誤差指標[14](ERGAS);②波譜角[15](spectral angle mapper,SAM);③廣義通用圖像質量指標[16](Generalization of the universal image quality index,GUIQI)。其中,ERGAS和SAM的值越小,代表著融合性能越好。與此同時,GUIQI的值越大越好。 表2~表4分別給出了多個算法在高光譜數據集Botswana、Washington DC Mall與Indian Pines的融合性能評估結果。其中,較好的融合結果使用粗體表示。此外,P+H用于表示全色圖像與高光譜圖像的融合方式。(P+M)+H代表著先進行多光譜圖像與全色圖像的融合,然后再與高光譜融合的方式。P+(M+H)代表著先進行多光譜圖像與高光譜圖像的融合,然后再與全色圖像融合。P+M+H表示同時進行多光譜圖像、高光譜圖像、全色圖像的融合方式。 觀察表2~表4中的融合性能評估結果,我們可以發現本文所提出的算法具有較好的融合性能。通過對比,我們可以發現不同的融合算法具有不同的多源多波段圖像融合與圖像細節的建模及挖掘能力。最后,基于融合性能指標ERGAS、SAM和GUIQI的定義,本文所提出的算法可以融合較多的局部細節信息。 表2 基于Botswana數據集的多源多波段圖像融合性能定量分析結果 表3 基于Washington DC Mall數據集的多源多波段圖像融合性能定量分析結果 表4 基于Indian Pines數據集的多源多波段圖像融合性能定量分析結果 為了在視覺上進行融合質量評估,本文給出了Botswana與Indian Pines數據集的多源多波段圖像融合結果(Washington DC Mall數據集與Botswana數據集的處理視覺效果基本相同),如圖1和圖2所示。其中,高光譜圖像的信噪比是30 dB;多光譜圖像的信噪比是30 dB;全色圖像的信噪比是40 dB。其中,P+H代表著全色圖像與高光譜圖像的融合;(P+M)+H代表著先融合全色圖像與多光譜圖像,然后再與高光譜進行融合;P+(M+H)代表著先融合多光譜與高光譜圖像,然后與全色圖像進行融合。 圖1(d)和圖2(d)給出了本文提出算法的融合結果。其中,圖1(d)所顯示的融合結果包含有波段(32 26 6);圖2(d)所顯示的融合結果包含有波段(30 22 3)。從中我們可以看到,本文提出的算法具有較好的融合效果,細節信息比較多。這些視覺上的融合效果驗證了本文提出的算法的有效性。 圖1 基于Botswana數據集的多源多波段圖像融合視覺結果對比分析 圖2 基于Indian Pines數據集的多源多波段圖像融合視覺結果對比分析 為了對不同融合算法的時間復雜度進行定量分析,本文在同等條件下,通過測量算法運行時間的方式,進行性能評估,對基于Indian Pines數據集的處理比較(對Botswana和Washington DC Mall數據集處理具有相同比例的效果,因為算法相同只是數據不同而已)如表5所示。其中,運行時間較少的算法是FUSE算法。但是,結合之前的性能評估結果,我們可以看到所提出的算法只增加了一些計算時間,但是具有較好的融合性能。 表5 基于Indian Pines數據集的算法運行時間對比單位:s 本文針對多源多波段圖像融合問題,引入復合正則化方法,提出了一種基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合模型。該正則化方法包含有全局稀疏梯度正則項與低秩張量正則項。本文采用基于ADMM優化框架求解融合模型。本文所提出的方法可以實現了三種視覺傳感器圖像的同時融合。仿真實驗及融合性能評估結果驗證了本文所提出算法的有效性。本文的理論與技術成果為基于多傳感器融合的目標檢測與識別提供理論與技術基礎。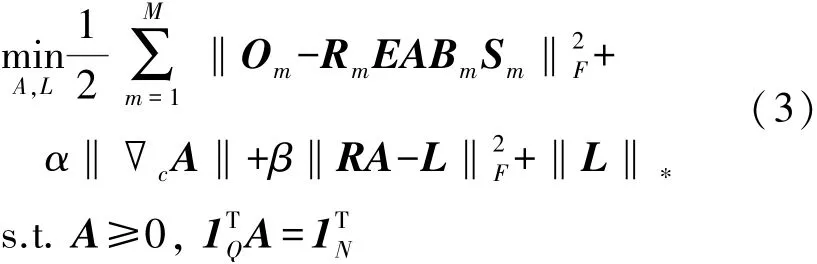
2 基于全局稀疏梯度與低秩張量正則化的多源多波段圖像融合
2.1 交替最小化框架

2.2 求解子問題

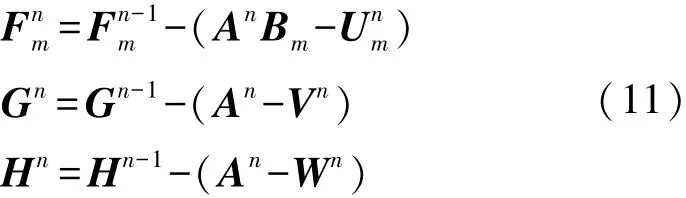

3 實驗結果與討論
3.1 數據集及仿真實驗參數
3.2 實驗結果


4 結論

